初中生數學態度量表的編制及信度效度檢驗

何小亞，李耀光

（1．華南師范大學 數學科學學院，廣東 廣州 510631；2．佛山市第二中學，廣東 佛山 528000）

1 問題的提出

在過去一段時期，中國數學教育比較關注教學方法與教學內容以及學習方法與學習成績，而忽略培養學生良好的數學態度．《全日制義務教育數學課程標準（實驗稿）》指出，使學生獲得對數學理解的同時，在思維能力、情感態度與價值觀等多方面得到進步和發展[1]．這標志著對數學態度的培養已正式納入了數學新課程的目標體系，成為新時期中國數學教育的重要組成部分．

與之相伴，對數學態度的研究如雨后春筍般涌現．但不少成果還存在著一些不足，主要表現在：第一，直接將數學作為態度對象來研究的成果非常少見[2～3]，大多數研究只著重探討一種或極少數幾種與數學有關的心理現象[4～6]，沒有從更廣泛的心理意義來探究數學態度．第二，常見的一些數學態度量表[7～11]大多數存在維度欠清晰，指標欠全面，信效度殘缺，甚至沒有等問題，缺乏實際的可操作價值．第三，信效度較高，結構完整且維度清晰的初中生數學態度量表目前還沒有出現．據此，初中生數學態度量表的編制研究將具有十分重要的理論和實踐意義．

2 數學態度模型的建構

2.1 概念界定

數學態度是個體對數學所持有的一種相對穩定的心理結構和選擇性傾向，它以數學為指向對象，可分為對數學的認知、情感和行為傾向3種成分．

2.2 模型構想

態度是指個人對客觀現實的某種選擇性傾向，主要包括認知、情感和意向（行為傾向）3種成分，客觀現實包括個人經歷和接觸到的一切人、事、物、過程、現象和關系等[12]．態度是一個多層面、多維度的系統，在多重維度上形成單一的態度是當今態度研究中的一個重要思想，而且任何一種心理活動，只要具備認知、情感和行為傾向3種因素，就可稱為態度[13]．態度的測量從嚴格意義來說是多維度的[7]．

對理論進行梳理，構建出如圖1所示的初中生數學態度模型[14]．它是一個多層面和多維度的心理系統，可分為學科態度和學習態度兩個方面．學科態度是指個體將數學看作一門學科知識時所持有的觀點；學習態度是指個體在學習數學過程中所獲得的心理體驗．

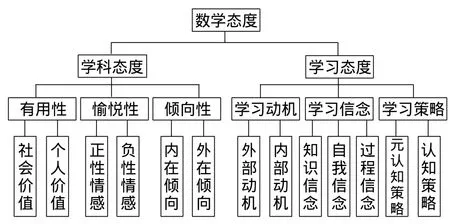
圖1 初中生數學態度模型（MAMHL）

3 初中生數學態度預測量表的編制

初中生數學態度預測量表共有 93道題（見文[14]中的附錄7），具體包括78道數學態度題，8道可信度量表題和7道自我投入分量表[10]題．數學態度題包含26道反向題，占全部數學態度題的三分之一．這93道題主要通過4種途徑來獲得．

3.1 開放式問卷調查

隨機選取廣州市內的兩所中學，再從各年級中隨機抽取10人（男女各半，共60名初中生）進行問卷調查，并與這兩所學校的全體初中數學老師進行訪談．問卷有5個大題：（1）你為什么學習數學，你是怎樣學習數學的？（2）你覺得數學是一門有趣的課程嗎？請你談談對數學的感受．（3）你認為數學在你的學習和日常生活等方面有哪些重要影響？請簡要地把這些影響寫出來．（4）有人說：“數學就是計算，數學就是證明．”你同意這種說法嗎？如果不同意，那么你認為數學是什么呢？（5）從明天開始，如果每周增加兩節數學課，你會高興嗎，為什么？問題（1），（3），（4）、（2）和（5）分別反映個體對數學的認知、情感和行為傾向成分．

3.2 文獻資料查閱與引用

與數學態度有關的常見量表有數學或科學態度量表[8]、數學課態度量表[9]、數學學習經驗問卷[10]和數學學習態度量表[11]等．雖然這些量表的信度和效度參數不夠齊全，但是被研究者引用并進行研究的情形仍然較為常見．

3.3 專家經驗與指導

一是借鑒專家的研究經驗，如“學習數學，就是老師舉例子，我們照著做”；“每個數學題的條件不會少，也不可能多，否則就是題目錯了”[15]．二是采用專家指導下的自行命題方式，如“只要能算出正確答案，對解題過程的理解并不重要；當解題受阻時，我會先從頭至尾檢查自己的解題過程；不同的學習階段，我會為自己制訂相應的數學學習目標”．

3.4 可信度量表與效標量表的確定

可信度量表的編制參考張友福的可信度量表[16]，題目與記分方式見文[14]中的附錄1．選擇投入動機量表[10]作為效標量表，包括工作投入和自我投入兩個分量表，因為態度與動機是雙向的[7]．有研究證實，投入動機、工作投入與自我投入量表的內部一致性α系數分別為0.804 2、0.786 9和0.802 5[17]．

4 初中生數學態度預測量表的試測與分析

4.1 被試與試測

采用分層抽樣和隨機抽樣方式．隨機選擇廣州市內的4個區，在各區內隨機選擇一所初中學校：學校 A為重點中學；學校B為普通中學；學校C與學校D介于重點與普通中學之間．在每所學校的每個年級以班為單位隨機選擇被試，采取匿名和自愿測試的原則．

試測時共隨機發放初中生數學態度預測量表問卷 620份，實際自愿回收問卷516份．問卷篩選需經過兩個步驟：（1）目測．有以下情形將視為無效問卷：未應答題目大于等于兩個；出現選兩個以上答案的題目；存在同一性、規律性或周期性應答等情形．（2）可信度檢驗．用可信度量表對經過目測篩選后的問卷再進行檢驗，獲有效問卷455份，有效率占自愿回收問卷的88.2%．

4.2 項目分析

對反向題進行反向記分，用±3σ（標準差）檢驗法進行異常值檢驗，全部78道數學態度題的得分均在正常范圍內．接著，按兩個步驟進行項目分析：一是用題總相關法對題目得分與數學態度總分之間作相關分析[18]，刪除相關系數在0.2以下的3道題以后，余下75道題．二是用臨界比率（CR）法逐步排除均值沒有達到顯著的題項[10]，將與每題相對應的數學態度得分排序，得分前27%為高分組，得分后27%為低分組．對高低二組的每題得分均值用獨立樣本t檢驗，顯示余下的 75道數學態度題均有顯著性差異（P＜0.05）．

4.3 探索性因素分析

探索性因素分析在于探求量表的結構效度，用 SPSS 13.0軟件，用主成分分析法和最大方差旋轉法．因子數目確定有3個原則[10]：（1）因子特征值大于1．（2）因素群符合陡階檢驗．（3）每個因子至少包含3道題目．因子命名有兩個原則：（1）如果某個因子的題目主要來自數學態度模型中的某個三級指標，就參考該指標進行命名．（2）如果某個因子中一半以上的題目負荷值都比較高，就參考這些題目表達的共同心理因素進行命名．

經檢驗，各三級指標的 KMO值至少在 0.773以上，Bartlett X2值顯著（P＜0.01），說明可以作因素分析，其因子結構及因子載荷由表1～表6所示．

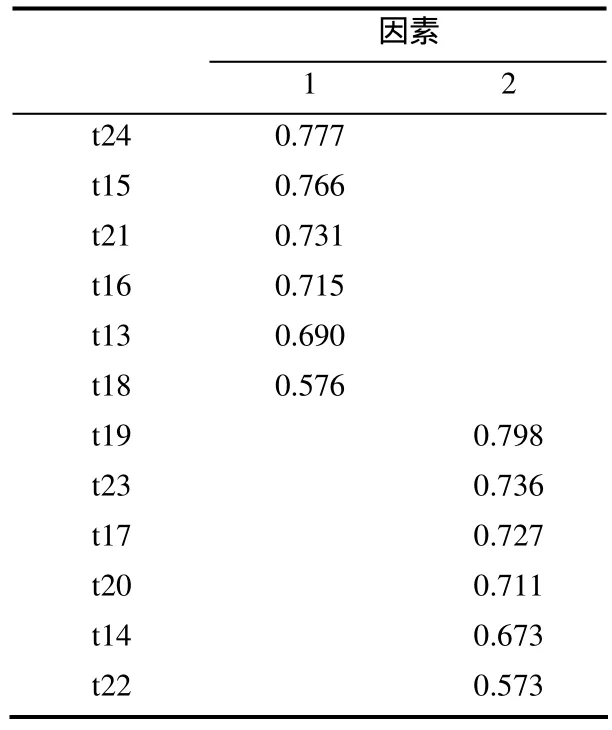
表2 愉悅性因子結構及載荷

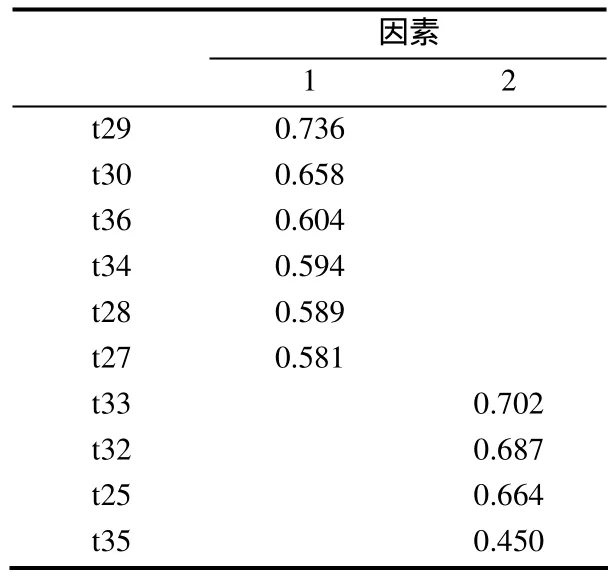
表3 傾向性因子結構及載荷

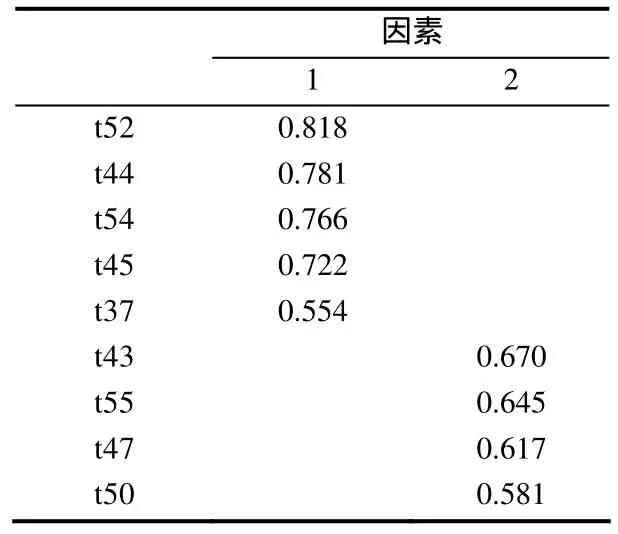
表4 學習動機因子結構及載荷

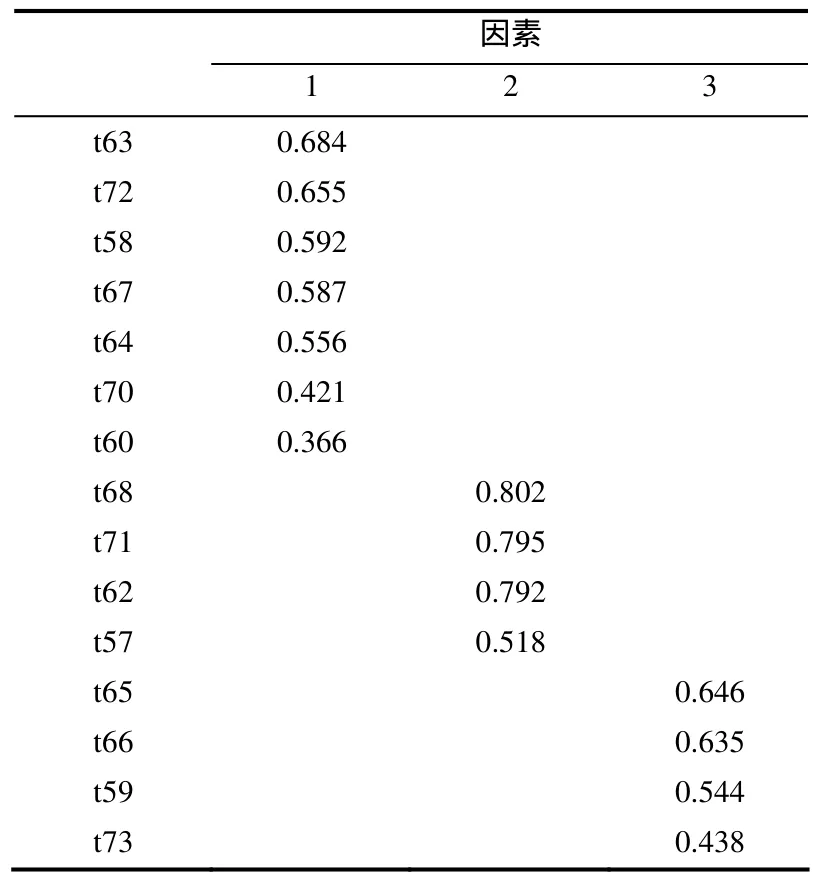
表5 學習信念因子結構及載荷

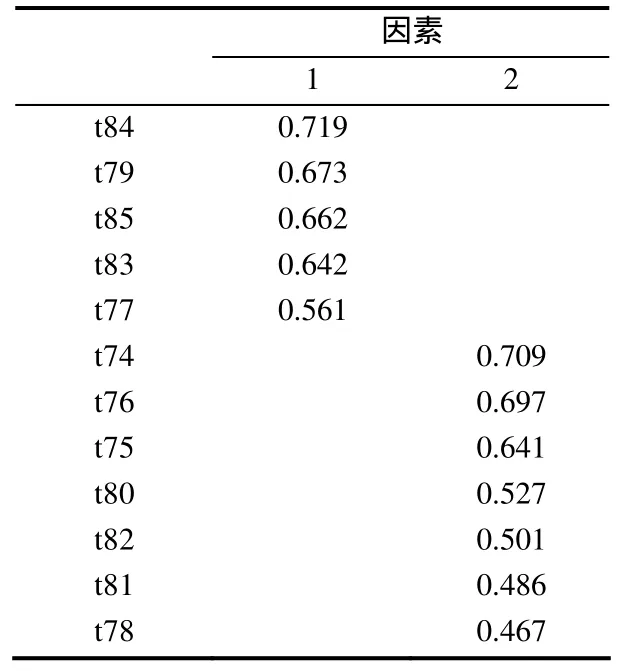
表6 學習策略因子結構及載荷

分析表明，初中生數學態度預測量表中的75道數學態度題可精簡為68道題，依次對各因素進行命名[14]：

（1）題目t7、t6、t9、t8、t2主要是指數學對個體發展的價值，命名為個體價值；題目 t4、t11、t5、t3、t12主要體現數學對社會發展的促進作用，命名為社會價值．

（2）題目 t24、t15、t21、t16、t13、t18是指對數學的愉快體驗，命名為正性情感；題目t19、t23、t17、t20、t14、t22是指對數學的不愉快體驗，命名為負性情感．

（3）題目 t29、t30、t36、t34、t28、t27是指由于喜愛數學而產生的內在心理行為，命名為內在傾向；題目t33、t32、t25、t35是因為對數學的喜好或厭惡而產生的外顯心理特征，命名為外在傾向．

（4）題目t52、t44、t54、t45、t37是指由于對數學或數學學習有興趣而產生的學習動機，命名為內部動機；題目t43、t55、t47、t50是指為了得到某種贊揚，克服某種困難或要增強某種能力而產生的數學學習興趣，命名為外部動機．

（5）題目 t63、t72、t58、t67、t64、t70、t60主要是指對數學知識的看法或認識，命名為知識信念；題目t68、t71、t62、t57主要體現對數學學習的信心或把握程度，命名為自我信念；題目t65、t66、t59、t73主要反映對數學學習的過程的看法或認識，命名為過程信念．

（6）題目t84、t79、t85、t83、t77主要體現數學學習中的自我調節或自我監控等認知方式，命名為元認知策略；題目t74、t76、t75、t80、t82、t81、t78主要是指數學學習中采用的常識性認知方式，命名為認知策略．

4.4 驗證性因素分析

驗證性因素分析在于檢驗量表的結構效度，有兩種常見方式：一是將調查問卷分成兩部分，一部分做探索性因素分析，另一部分做驗證性因素分析[19]．二是先用數理統計軟件如SPSS 13.0作探索性因素分析以探測數據結構，再用結構方程軟件如 LISREL 8.70作驗證性因素分析[20]以分析比對假設模型與實測數據之間的差異性[21]．結構方程模型下的驗證性因素分析可以幫助了解各題目與指標的歸屬是否正確，有沒有錯誤地歸屬于沒有關系或關系不大的因子，以達到評價及修正模型的目的．用絕對或相對擬合指數來評價模型的擬合效果，前者常用卡方值 X2和近似誤差均方根RMSEA，后者推薦使用非范擬合指數 NNFI和比較擬合指數CFI．一般地，卡方值與自由度df的比值在2.0～5.0之間，RMSEA經驗值在0.08以下，數值越小表示模型擬合越好；NNFI和 CFI在 0～1之間，數值越接近 1表示模型擬合越好[22]．

根據以下原則刪除或重新評估題目的歸屬關系[21～22]：（1）單次模型擬合時，各指標只刪除一個或最多兩個題目．（2）題目的因子負荷在 0.34以下，且在其它因子上的修正指數MI在32以下時，直接刪除該題目．（3）題目的因子負荷和完全標準化解都在0.5以下，且在其它因子上的MI在32以下時，視情況可刪除該題目．（4）題目的因子負荷和完全標準化解都在0.5以下，但在其它某個或某幾個因子上的MI在40以上時，需重新評估該題目的因子歸屬關系，又分兩種情形：如果題目歸屬于新的因子后，負荷和標準化解都在0.5以上，因子負荷的t檢驗顯著（t≥2），且在其它各因子上的MI在32以下時，認為該題目的新歸屬關系成立；如果題目歸屬于新的因子后，在某個或某幾個因子上的MI反而更高時，表明新歸屬關系比原來的歸屬關系差，將該題目刪除．

結果顯示，相對最佳的初中生數學態度擬合模型有 53道題．擬合指標方面，X2/df為1.99，RMSEA為0.046，NNFI為 0.96，CFI為 0.96，最大 MI為 27.96．因子負荷方面，0.51～0.99與0.41～0.49之間分別有41與12道題，沒有小于0.34被建議應該刪除的題目．

5 初中生數學態度量表的正式確定及信效度檢驗

用相關法精簡負性情感維度，刪除題項t20，正式確定初中生數學態度量表（MASHL）由52道題目組成（見文后的附錄）．這份量表是在數學態度概念與初中生數學態度模型的理論基礎上，廣泛參考國內外相關研究成果[23～26]編制而成的．

5.1 信度檢驗

5.1.1 內部一致性α系數和Rulon分半信度

投入動機、工作投入和自我投入量表的內部一致性α系數分別為0.722、0.803和0.752，效標量表信度較高．各三級指標只有3～5道題，長度短，不探求Rulon分半信度而只檢驗其α系數，分別是個體價值0.732、社會價值0.632、正性情感0.839、負性情感0.816、內部傾向0.651、外部傾向0.449、內部動機0.806、外部動機0.775、知識信念0.662、自我信念0.766、過程信念0.533、元認知策略0.730和認知策略0.695．

然而對于不只包含一個因素的測驗，分半信度系數是比較正確的估計方法[27]．將難度系數定義為所有被試在題目上的平均得分與該題目的最高應答5分的比值，將52道題的難度系數由高到低進行排列，依排序分成奇數與偶數兩個題目組，可算出Rulon分半信度．

有研究表明，α系數與Rulon分半信度均與題目數量有關，題目越多，信度越高[27]．如表 7所示，傾向性指標只有7道題，雖然題目不多，但其α系數與Rulon分半信度也分別達到了0.62和0.671．數學態度量表、學科態度與學習態度分量表的α系數分別為 0.926、0.894和 0.844；Rulon分半信度分別為0.922、0.905和0.881，都達到了人格測驗的信度應在0.8以上的建議標準[27]．

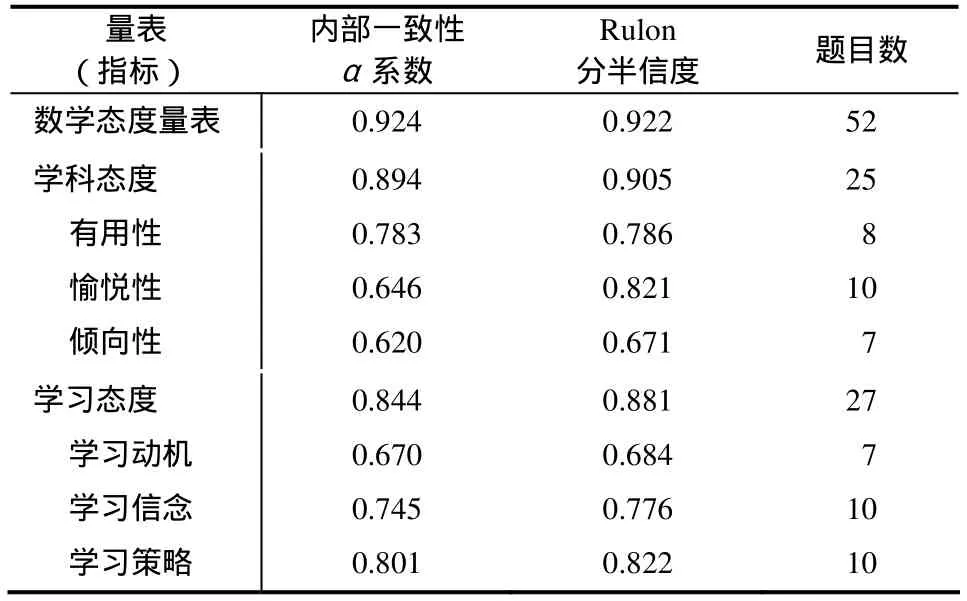
表7 量表或指標的信度檢驗及題目數

5.1.2 相關性檢驗

當人格測驗中的量表或分量表如果包含多個指標時，屬異質性測驗，應同時報告總量表與各分量表以及與各指標之間的相關[18]．限于篇幅，只列出數學態度與一級、二級指標間的相關系數（如表 8）．在相同層面內，各指標間的相關系數都在中等程度（0.3～0.8）或偏下．在不同層面間，各指標間的相關系數絕對多數地在中等程度或偏上，達到了人格測驗的相關性檢驗標準[28]．

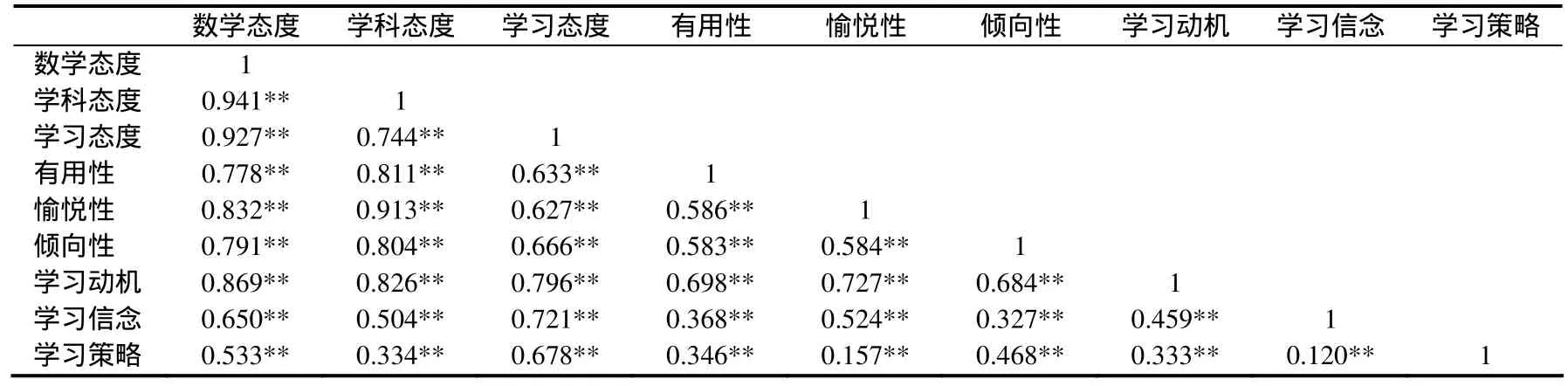
表8 數學態度與一級指標及二級指標間的相關性檢驗

5.1.3 重測信度

關于重測信度，華南師范大學心理學院王才康教授認為：“一般地，在量表的正規化編制過程中，在求量表信度時可優先檢驗量表的分半信度、內在一致性信度與相關性系數，而對重測信度可以留待日后有條件了再去研究．”由于實際條件限制，在相隔不太長的時間內，對被試總體進行較大規模的重復測試，存在不少實際困難，研究者將在條件許可時，繼續對初中生數學態度量表的重測信度進行研究，以擴大其普適性，也歡迎有興趣的讀者對其進行研究與檢驗．

5.2 效度檢驗

測驗效度分為內容效度、效標關聯效度和結構效度 3大類．人格測驗的效標關聯效度應該在 0.30以上；內容效度通常由專家判斷；如果探索性因素分析得出的因子結構被驗證性因素分析證明是最佳模型時，就認為該測驗具有較好的結構效度[28]．限于篇幅，省去對內容效度的陳述．

5.2.1 效標關聯效度

數學態度量表、學科態度和學習態度分量表與投入動機量表的效標關聯效度分別為0.502、0.471和0.466，在0.01水平下呈顯著性意義，達到了效標關聯效度應該在0.3以上的標準[28]．

5.2.2 結構效度

用兩種方法檢驗：

（1）相關法，檢驗題目與各指標間的相關程度．當問卷所需要的題目和測驗的相關系數在0.32～0.80范圍時，這些題目能為測驗提供滿意的信度和效度．在 0.01顯著性水平下，學科態度分量表有21道題（約84%）與三級指標，27道題（100%）與二級指標，26道題目（約96%）與一級指標的相關系數均在 0.32～0.80以內；學習態度分量表有 19道題（約70.4%）與三級指標，29道題（100%）與二級指標，27道題（約92.6%）與一級指標的相關系數均在0.32～0.80以內．數學態度量表的全部52道題中，有46道題（約84.6%）與數學態度測驗總分的相關系數在0.32～0.80以內，余下6道題均在0.162～0.310范圍內但偏上．

（2）結構方程模型法，探討量表的結構效度．用一階結構方程模型和 LISREL 8.70軟件驗證了題目與三級指標間的歸屬關系，而一級、二級和三級指標間及其與題目間的直接或間接的歸屬關系，有時需要用高階結構方程模型才能驗證．擬合指數顯示，卡方值與自由度之比 X2/df、近似誤差均方根RMSEA、非范擬合指數NNFI和比較擬合指數CFI均達到了結構方程理論所提出的參數標準[22]，表明量表的結構效度較高．

6 討論與結論

問卷調查與測試均采取匿名和自愿回收原則，而且經過嚴格的目測與可信度檢驗等兩輪篩選，從而減少了有效問卷中的應答誤差，提高了量表的編制質量．正式的初中生數學態度量表共有52道題，分為學科態度與學習態度兩個分量表．學科態度分量表有25道題，分為有用性、愉悅性和傾向性共3個維度；學習態度分量表有27道題，分為學習動機、學習信念和學習策略共3個維度．

初中生數學態度量表、學科態度與學習態度分量表的內部一致性α系數至少在0.844以上；Rulon分半信度至少在0.881以上；初中生數學態度量表與各分量表以及與各指標間的相關系數絕對多數地在中等程度范圍且偏上．初中生數學態度量表、學科態度與學習態度分量表的效標關聯效度至少在 0.466以上，大于 0.30的人格測驗效標關聯效度標準[28]；一階與高階結構方程模型分析顯示量表的結構效度較好．初中生數學態度量表具有維度清晰、結構完整、指標較全面、信效度較高等特點，可作為初中生數學態度領域的一個可信且有效的心理測評工具．

[1]中華人民共和國教育部．全日制義務教育數學課程標準（實驗稿）[M]．北京：北京師范大學出版社，2011．

[2]姚靜．關于數學態度學習的心理分析[J]．數學教育學報，2001，10（3）：32-35．

[3]焦璨，吳利，張敏強，等．澳門私立學校初三學生數學態度與數學焦慮的關系研究[J]．教育導刊，2010，（1）：43-45．

[4]臧向紅，王曉陽．中學生數學學習態度芻議[J]．數學教育學報，1993，2（2）：67-72．

[5]李明振．成就動機、數學學習態度與學生數學學業成績的關系[J]．貴州師范大學學報，1994，（2）：45-51．

[6]姚梅林，杜春麗．學習信念的心理學研究[J]．信陽師范學院學報（哲學社會科學版），2004，（2）：11-14．

[7]Lewis R Aiken．態度與行為理論、測量與研究[M]．何清華譯．北京：中國輕工業出版社，2008．

[8]Lewis R Aiken．心理測量與評估[M]．張厚粲，黎堅譯．北京：北京師范大學出版社，2006．

[9]陳國鵬．心理測驗與常用量表[M]．上海：上海科學普及出版社，2005．

[10]吳明隆．SPSS統計應用實務[M]．北京：中國鐵道出版社，2000．

[11]趙鵬程．小學生積極的數學學習態度形成的訓練研究[D]．內蒙古師范大學，2007．

[12]古茂盛．人格心理學[M]．北京：中國醫藥科技出版社，2006．

[13]梁娟，范曉玲．態度研究的過去、現在和未來[J]．法制與社會，2008，（4）：291-292．

[14]李耀光．初中生數學態度量表的編制及其應用[D]．華南師范大學，2011．

[15]李士锜．PME：數學教育心理[M]．上海：華東師范大學出版社，2001．

[16]張友福．中學數學教學中非智力因素培養方法研究[D]．湖南師范大學，2006．

[17]王愛平，車宏生．學習焦慮、學習態度和投入動機與學業成績關系的研究[J]．心理發展與教育，2005，（1）：55-59．

[18]Sandra A Mclntrice．心理測量[M]．駱方，孫曉敏譯．北京：中國輕工業出版社，2009．

[19]張沖，孟萬金．中國教師積極心理品質量表的編制研究[J]．中國特殊教育，2011，（2）：58-64．

[20]鄒循豪，陳俊欽．高校體育教師心理契約量表的編制與信效度檢驗[J]．武漢體育學院學報，2011，（4）：57-61．

[21]邱皓政，林碧芳．結構方程模型的原理與應用[M]．北京：中國輕工業出版社，2009．

[22]侯杰泰，溫忠麟，成子娟．結構方程模型及其應用[M]．北京：科學出版社，2004．

[23]Barara K Hofer, Paul R Pintrinch. The Development of Epistemological Theories: Beliefs about Knowledge and Knowing and Their Relation to Learning [J]. Review of Educational Research, 1997, 67(1): 89.

[24]Barbare K Hofer. Personal Epistemology Research: Implications for Learning and Teaching [J]. Journal of Educational Psychology Review. 2001, 13(4): 353-360.

[25]Schoenfeld A. Explorations of Students Mathematical Beliefs and Behavior [J]. Journal for Research in Mathematics Education, 1989, 20(4): 358-355.

[26]楊之．世紀婚約——哲學與數學教育聯姻的實踐與思考[M]．大連：大連理工大學出版社，2009．

[27]王孝玲．教育測量[M]．上海：華東師范大學出版社，2008．

[28]凌文輪，方俐洛．心理與行為測量[M]．北京：機械工業出版社，2004．