基于支持向量機的網絡輿情混沌預測

黃敏，胡學鋼

1.安徽廣播電視大學，合肥 230022

2.合肥工業大學計算機與信息學院，合肥 230009

基于支持向量機的網絡輿情混沌預測

黃敏1，胡學鋼2

1.安徽廣播電視大學，合肥 230022

2.合肥工業大學計算機與信息學院，合肥 230009

1 引言

網絡輿情是社會輿情的重要組成部分，相對于傳統新聞媒體，它的互動性更強，用戶既是信息接收者，又是信息發起者，使得信息在網絡上傳播更加及時和迅速，負面的網絡輿情將會對社會公共安全形成較大威脅，因此對網絡輿情變化進行分析和建模，并對其發展趨勢進行預測，可以幫助有關部門制定正確的輿論引導策略，對維護社會和諧穩定具有重要的現實意義[1-2]。

當前網絡輿情預測方法主要分為兩類：傳統統計學預測方法和機器學習預測方法。傳統統計學預測方法有自回歸（AR）、滑動平均（MA）、差分自回歸移動平均（ARIMA）等[3-5]。該類方法簡單、易實現，尤其是ARIMA極具彈性，它可表示各種不同種類的時間序列模型，融合了時間序列分析和回歸分析的優點，在網絡輿情變化預測應用最為廣泛，然而ARIMA是一種線性預測模型，網絡輿情變化受到多種因素的影響，具有非線性，ARIMA無法捕捉網絡輿情變化的非線性變化特點，從而影響了預測精度[6]。機器學習算法主要有人工神經網絡（ANN）、支持向量回歸機（SVR）等。該類方法基于非線性理論建模，可以更加準確地描述網絡輿情變化，較傳統的線性預測模型，預測精度得到進一步提高，結果更加理想[7-10]。由于網絡輿情有人的參與，用戶有自己的偏好和思想，導致網絡輿情具有較強混沌性，當前機器學習算法均忽略了網絡輿情的混沌特性，因此建立的模型不能全面、準確描述網絡輿情變化，預測準確性有待進一步提高[11]。

針對網絡輿情變化的混沌性，將混沌理論引入到網絡輿情建模預測中，并與SVR相結合，提出一種基于相空間重構和支持向量回歸機相融合的網絡輿情預測模型（PHR-SVR），并通過仿真實驗驗證PHR-SVR的有效性。

2 網絡輿情相空間重構及混沌性識別

相空間重構是混沌理論的基礎，主要思想是：系統任一分量的演化是由與其相互作用的其他分量決定的，它的相關分量的信息隱藏在這一分量的演化過程中，因此可以通過分析某一分量的時間序列，了解原系統的動力學特性，提取和恢復出原系統的規律[12]。

設時間序列為：x(t),t=1,2,…,N，通過選擇合適的嵌入維數m和延遲時間τ，就可以對其進行重構，得到一個多維向量序列X(t)，從而挖掘隱藏于時間序列的信息，恢復原動力系統。

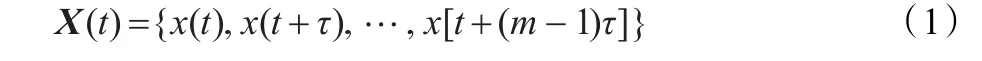
式中，M=N-(m-1)τ，M為相點個數。

2.1 樣本數據來源

選擇“長春嬰兒隨車被盜案”作為網絡輿情的源事件，由于天涯社區是鳳凰網和艾瑞咨詢集團共同發布的“全球中文論壇100強”中排名第一的論壇，在知名度和影響度上具有優勢，其數據具有代表性，因此選擇天涯社區中的論壇數據作為網絡輿情的數據源。從2013年3月4日上午10時天涯社區中出現第一個關于“長春嬰兒隨車被盜案”事件的源帖開始，到2013年3月8日10時為止，共采集96小時的帖子數作為研究對象，具體如圖1所示。

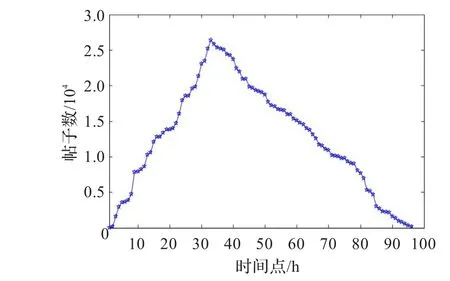
圖1 收集的網絡輿情數據

2.2 數據預處理

從圖1可知，網絡輿情變化范圍比較大，為了避免取值范圍大的數據淹沒了取值范圍小的數據；且SVR核函數的值依賴于特征向量的內積，數據過大會對訓練過程產生不利影響，為此，在數據輸入到SVR之前對其進行歸一化處理，歸一化公式為：

式中，x′表示歸一化后的值，xmax和xmin分別表示最大值和最小值[13]。

2.3 網絡輿情相空間重構

2.3.1 互信息法計算延遲時間

（1）構建網絡輿情量時間序列{x(t)}的二維相圖，令(x,y)=[x(t),x(t+τ)],τ=1。

（2）在二維相圖中畫出吸引子的矩形框，并將矩形框劃分成等間距的小格子，x0和y0是格子的起始點，Δx和Δy分別是x和y方向上小格子的長度，Mx和My分別是x和y方向上格子的數目。

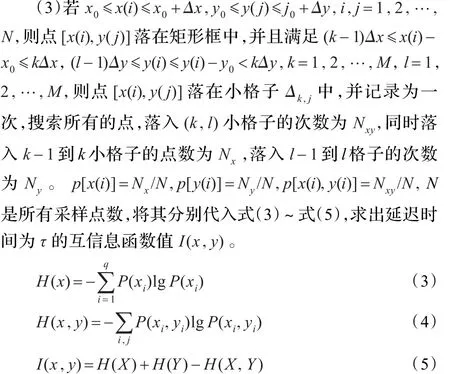
式中，H(X)代表X的不確定程度，P(xi)是xi發生的概率，q為狀態總數，H(X,Y)為X和Y的聯合信息熵，P(xi,yi)為事件xi與yi同時發生的聯合概率。

（4）令τ=τ+1，返回步驟（2）。

網絡輿情時間序列的互信息函數變化曲線如圖2所示。從圖2可知，當τ=3時，互信息函數達到第一極小值，所以網絡輿情時間序列的τ=3。

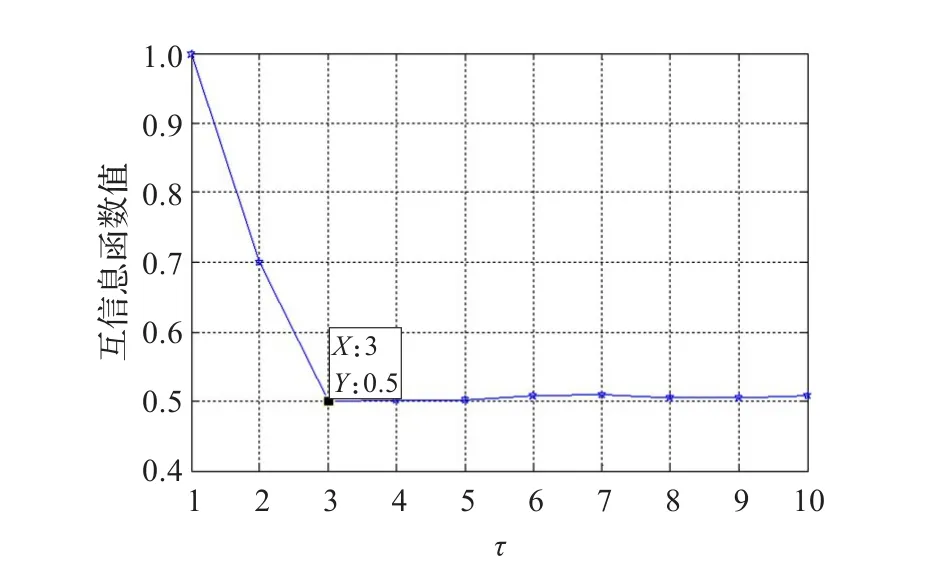
圖2 網絡輿情的延遲時間計算

2.3.2 G-P法選擇嵌入維數

（1）根據互信息法求出τ=3，嵌入維數的初值為m=1。

（2）選擇合適的臨界距離r，根據式（6）計算Cn(r)，向量距離采用∞范數計算，即兩個向量最大分量差作為向量距離。

式中，M為相點的個數，r為臨界距離，θ為Heaviside單位函數。

（3）用最小二乘法擬合lgC(r)n～lgr曲線中的直線段，直線的斜率為關聯維數D。

（4）增加嵌入維數，即m=m+1，返回步驟（2）。

網絡輿情時間序列在不同嵌入維數下的關聯維數，如圖3所示。從圖3可知，當嵌入維數m=5時，關聯維數達到飽和狀態，這表明網絡輿情時間序列的最優m=5。

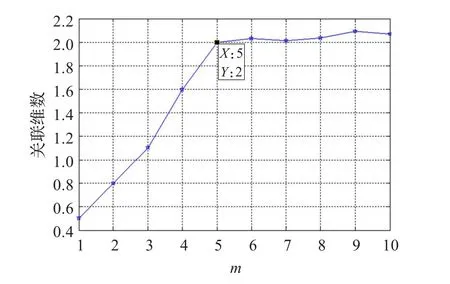
圖3 網絡輿情的嵌入維數計算

2.4 網絡輿情時間序列的混沌性識別

混沌系統具有對初始值敏感的特性，若系統的最大Lyapunov指數λ1＞0，則該系統一定是混沌的。基于小數據量法求取最大Lyapunov指數計算步驟如下：

（1）對時間序列x(t),t=1,2,…,N，進行快速傅里葉變換，計算出平均周期p。

（2）利用互信息法計算延遲時間τ。

（3）根據延遲時間τ和嵌入維數m重構相空間X(t),t= 1，2，…，M。

（4）找相空間中每個點X(t)的最近鄰點X(t?)，并限制短暫分離，即

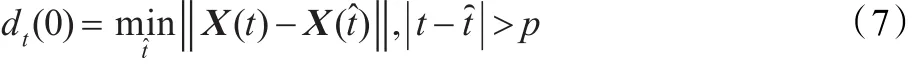
式中，t=1,2,…,M。

（5）對相空間中每個點X(t)，計算出該鄰域點對的i個離散時間步長后的距離dt(i)。

式中，q為非零dt(i)的數目，并用最小二乘法做出回歸直線，該直線的斜率為最大Lyapunov指數。

通過計算得到網絡輿情時間序列的平均周期p=1，嵌入維數m=5，延遲時間τ=3，利用最小二乘法擬合直線，其斜率為最大Lyapunov指數，得到λmax=0.001 52＞0，這表明，網絡輿情時間序列具有弱混沌特性。

2.5 支持向量機算法

2.5.1 支持向量機回歸

支持向量機是一種基于統計學習理論的機器學習算法，在模型的復雜性和學習能力之間尋求最佳折衷，以期獲得最好的推廣能力[14]。SVR的回歸估計函數為：

式中，w表示權向量，b表示偏置向量。

使得預測的期望風險函數最小：

在求解實際問題時，只需利用支持向量進行求解，于是回歸估計函數為：

式中，σ為徑向基核函數的寬度。

2.5.2 支持向量機回歸的網絡輿情預測模型

給定網絡輿情時間序列的數據集D={x(t),t=1,2,…,N}，取延遲時間τ=3，嵌入維數m=5，按照上述的相空間重構方法，就可以得到相空間域中的數據集為：D?={X(t), Y(t)},t=1,2,…,M，其中X(t)={}x(t),x(t+τ),…,x[t+(m-1)τ]，Y(t)=x(t+1+(m-1)τ)，t=1,2,…,M,寫成矩陣形式為：

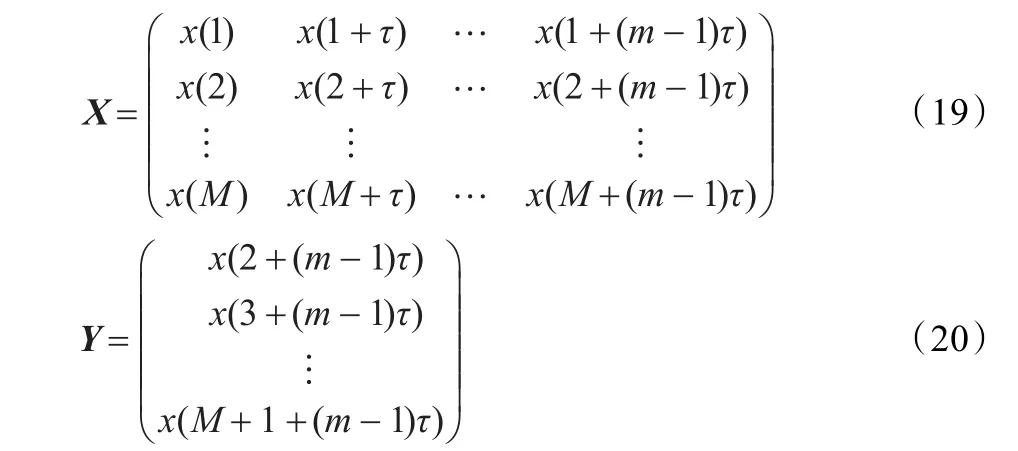
相空間域的預測模型就是用相空間中的點X(t)預測出Y(t)，即找到一個映射函數F，使得：

本文通過利用SVR來求取該映射函數，基于PHR-SVR的建模過程如圖4所示。

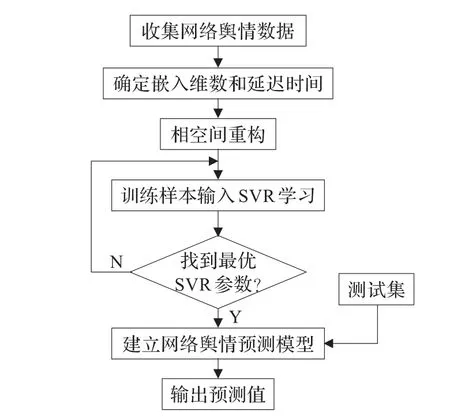
圖4 PHR-SVR的網絡輿情預測流程

3 預測實驗

3.1 仿真環境

在PIV 3.0 GHz CPU，2 GB RAM，操作系統為Windows 2000環境，通過VC++編程實現算法。采用ARIMA、SVR（沒有相空間重構）、PHR-BPNN作為對比模型。采用均方誤差（RMSE）和平均相對百分比誤差（MAPE）作為模型優劣評價標準。它們定義如下：

式中，xt和分別為實際值和模型預測值，n為樣本數。

3.2 結果與分析

3.2.1 一步預測

由于原始訓練樣本為65，而且最優嵌入維數為m=5，那么重構后就得到66-5=61個新的訓練集。首先采用含有61個數據進行訓練，并進行一步預測，然后將預測點的真實值加入到訓練集中，再進行一步預測，依此類推，最后得出30個測試集的一步預測值，再將最后預測值與測試集的真實值進行比較，并計算相應的RMSE和MAPE。BP神經網絡的結構為5-11-1；通過粒子群算法得到SVR最優的C=100，σ=1.715，ARIMA模型選擇ARIMA（3，2，2）。各模型對網絡輿情測試集的預測結果如圖5所示，它們相應的RMSE和MAPE見表1。

圖5 網絡輿情一步預測結果

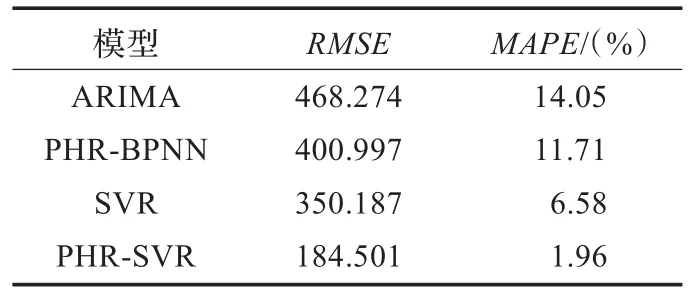
表1 各模型的一步預測性能對比

從表1和圖5的結果進行分析，可以得到如下結論：

（1）相對于ARIMA，PHR-SVR的網絡輿情預測精度大幅度提高，這主要由于ARIMA無法捕捉到網絡輿情時間序列的非線性變化特點，而PHR-SVR利用SVR的非線性預測能力有效提高了網絡輿情的預測精度。

（2）相對于SVR，PHR-SVR的網絡輿情預測誤差值更小，預測值與真實值十分接近，這主要由于PHR-SVR通過采用PHR挖掘隱含于網絡輿情時間序列的信息，可以更加準確、全面地對網絡輿情變化趨勢進行描述，得到更加可靠的預測結果，進一步提高了網絡輿情預測精度。

（3）相對于PHR-BPNN，PHR-SVR的預測結果始終比較穩定，且預測結果的RMSE、MAPE值遠遠小于PHR-BPNN，這主要由于SVR很好地克服了BP神經網絡過擬合、局部極小和網絡參數難以確定的難題，泛化能力更強，預測精度更高。

3.2.2 多步預測

網絡輿情預測時間一般要求有較大的提前量，采用一步預測（即僅對當前時間下一小時網絡輿情進行預測），既不能有效反映網絡輿情變化趨勢，也無法針對一些負面網絡輿情作出有效和及時的應對，因此，有必要將一步預測擴展到多步預測方法，于是采用多步預測法預測未來24 h的網絡輿情，所有模型均采用迭代法的多步預測法，即重復使用一步向前預測若干次，并把上一次的預測值視做系統輸出真值，應用于下一次預測中[15]。各模型的預測結果真實值與預測值對比見圖6。它們的RMSE和MAPE見表2。

從圖6和表2可以看出，ARIMA、SVR、PHR-BPNN網絡輿情的多步預測精度較低，誤差相當高，預測結果不可靠，預測結果實際應用價值較低，而PHR-SVR預測誤差明顯小于對比模型，而且PHR-SVR對網絡輿情變化的趨勢預測比較準確，預測性能要優于對比模型，預測結果具有較大的實際價值。

圖6 多步預測法的預測結果對比

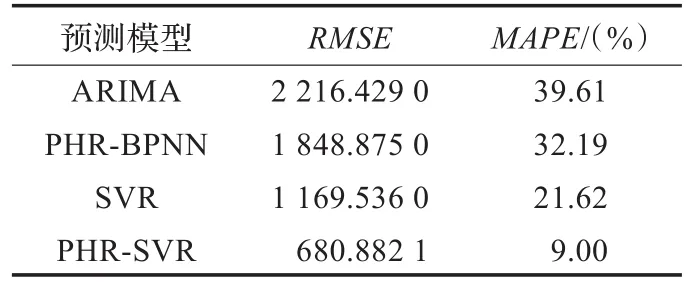
表2 各模型的多步預測性能對比

3.2.3 其他網絡熱點話題預測

為了使模型的性能更具說服力，采用2013年4月最熱門的話題“解放軍新式軍車號牌曝光”、“蘋果公司向中國消費者致歉”、“美媒體稱中國向中朝邊境調軍隊”、“浙江大姐中國式過馬路被罰，追著交警吐口水”、“日本允許臺灣漁船在釣魚島捕魚”、“劉志軍被曝光涉嫌受賄6千萬元”進行測試實驗，得到的一步預測誤差見表3。從表3可知，PHR-SVR獲得較好的預測精度，預測誤差控制在有效的范圍（5%）以內，結果表明，PHR-SVR是一種預測精度高、通用性好的網絡輿情預測模型。

表3 PHR-SVR對其他網絡熱點話題一步預測誤差

4 結束語

網絡輿情受到多種影響因素的綜合影響，具有時變性、混沌性，是一種復雜的變化系統，傳統預測算法難以建立準確的預測模型。針對網絡輿情的混沌變化特點，采用混沌理論和SVR建立了一種基于PHR-SVR的網絡輿情預測模型。結果表明：相對于對比模型，PHR-SVR提高了網絡輿情預測精度，預測結果更加穩定，更加準確描述了網絡輿情復雜的變化趨勢，預測結果有助于正確把握網絡輿情的發展，從而有助于科學合理地引導、管理各種網絡輿情傳播平臺，促進和諧社會構建工作的開展。

[1]王來華.輿情研究概論——理論、方法和現實熱點[M].天津：天津社會科學院出版社，2007.

[2]方薇，何留進，宋良圖.因特網上輿情傳播的預測建模和仿真研究[J].計算機科學，2012，39（2）：203-207.

[3]劉常昱，胡曉峰，司光亞，等.基于小世界網絡的輿論傳播模型研究[J].系統仿真學報，2006，18（12）：608-6l0.

[4]錢愛玲，瞿彬彬，盧炎生，等.多時間序列關聯規則分析的論壇輿情趨勢預測[J].南京航空航天大學學報，2012，44（6）：904-910.

[5]高輝，王沙沙，傅彥.Web輿情的長期趨勢預測方法[J].電子科技大學學報，201l，40（3）：440-445.

[6]張虹，鐘華，趙兵.基于數據挖掘的網絡論壇話題熱度趨勢預報[J].計算機工程與應用，2007，43（31）：159-161.

[7]方薇，何留進.采用元胞自動機的網絡輿情傳播模型研究[J].計算機應用，2010，30（3）：751-755.

[8]劉勘，李晶，劉萍.基于馬爾可夫鏈的輿情熱度趨勢分析[J].計算機工程與應用，2011，47（36）：170-173.

[9]周耀明，李弼程.一種自適應網絡輿情演化建模方法[J].數據采集與處理，2013，28（1）：69-75.

[10]Zeng J P，Zhang S Y，Wu C R，et al.Predictive model for Internet public opinion[C]//Fourth International Conference on Fuzzy Systems and Knowledge Discovery.Haikou：IEEE Press，2007：7-11.

[11]Zeng J P，Zhang S Y，Wu C R，et al.Modeling topic propagation over the Internet[J].Mathematical and Computer Modeling of Dynamic Systems，2009，15（1）：83-93.

[12]張春濤，馬千里，彭宏.基于信息熵優化相空間重構參數的混沌時間序列預測[J].物理學報，2010，59（11）：7623-7629.

[13]黃虎，蔣葛夫，嚴余松，等.基于支持向量回歸機的區域物流需求預測模型及其應用[J].計算機應用研究，2008，25（9）：2738-2740.

[14]趙云，肖嵬，陳阿林.基于加權支持向量回歸的網絡流量預測[J].計算機工程與應用，2012，48（21）：103-106.

[15]洪貝，胡昌華，姜學鵬.基于證據理論的迭代多步預測方法研究[J].控制理論與應用，2010，27（12）：1737-1742.

HUANG Min1,HU Xuegang2

1.Anhui Radio&TV University,Hefei 230022,China
2.School of Computer and Information,Hefei University of Technology,Hefei 230009,China

In order to improve the prediction accuracy of internet public opinion,this paper proposes an internet public opinion prediction model based on chaotic theory and Support Vector Regression.The internet public opinion time series proves to be with chaos characteristics,and then delay time and embedding dimension are calculated using mutual information method and G-P method respectively according to takens theorem,and the internet public opinion time series is reconstructed in phase space. The internet public opinion forecasting model is established using Support Vector Regression,and the simulation experiment is carried out with comparison models.The experimental results show that,compared with other models,the proposed model has improved the prediction accuracy and stability of internet public opinion and the prediction results have practical value.

internet public opinion;Support Vector Regression（SVR）;phase space reconstruction;chaotic theory

精確預測網絡輿情發展趨勢，對防止負面網絡輿情對公共安全威脅具有重要意義，針對網絡輿情變化的時變性、混沌性，提出一種基于支持向量機的網絡輿情混沌預測模型（PHR-SVR）。證明了網絡輿情具有混沌特性，根據Takens定理分別采用互信息法和G-P法確定延遲時間和嵌入維數重構網絡輿情時間序列相空間；在相空間中，利用支持向量回歸機（SVR）建立網絡輿情預測模型，與其他預測模型進行對比實驗。結果表明，相對于對比模型，PHR-SVR提高了網絡輿情的預測精度和可靠性，預測結果具有一定實用價值。

網絡輿情；支持向量回歸機；相空間重構；混沌理論

A

TP393

10.3778/j.issn.1002-8331.1307-0248

HUANG Min,HU Xuegang.Internet public opinion chaotic prediction based on Support Vector Regression machine. Computer Engineering and Applications,2013,49（24）：130-134.

安徽省教育廳自然科學基金（No.KJ2013B091）。

黃敏（1977—），女，講師，研究方向：數據挖掘；胡學鋼（1961—），男，教授，博士生導師，研究方向：知識工程，數據挖掘，數據結構。

2013-07-19

2013-09-04

1002-8331（2013）24-0130-05

CNKI出版日期：2013-10-17http://www.cnki.net/kcms/detail/11.2127.TP.20131017.1529.020.html