基于目標函數變化率的混合蟻群遺傳算法

劉雪東，許 峰

1.安徽理工大學 計算機科學與工程學院，安徽 淮南 232001

2.安徽理工大學 理學院，安徽 淮南 232001

基于目標函數變化率的混合蟻群遺傳算法

劉雪東1，許 峰2

1.安徽理工大學 計算機科學與工程學院，安徽 淮南 232001

2.安徽理工大學 理學院，安徽 淮南 232001

1 引言

隨著生命科學的迅猛發展，社會性動物（如螞蟻、鳥群、魚群等）的自組織行為引起了人們的廣泛關注。許多學者對這些動物的行為進行數學建模并用計算機對其進行仿真，群智能算法應運而生。

蟻群算法（Ant Colony Optimization，ACO）是近年來頗受國內外學者關注的一種新型模擬進化算法，由意大利學者Dorigo M于1992年首先提出[1]，Nature曾多次對蟻群算法的研究成果進行報道[2-4]。蟻群算法用蟻群在搜索食物過程中所體現出的尋優能力來解決優化問題，其算法的基本思想是模仿螞蟻依賴信息素，通過螞蟻間正反饋的方法來引導每個個體的行為。

遺傳算法（Genetic Algorithm，GA）于1975年由美國Michigen大學的J.Holland教授等人受生物進化論的啟發而提出的[5]。遺傳算法把生物進化過程中的自然選擇、優勝劣汰、適者生存和遺傳變異的思想應用到優化問題中，是一種全局隨機搜索算法。

蟻群算法具有分布式、自組織、正反饋等優點，缺陷是收斂速度較慢，易陷于局部最優解。遺傳算法的優點是自適應、并行性、具有較強的全局收斂性，缺陷是局部搜索能力較弱。

將兩種或多種智能優化算法按照某種規則相融合或在某種智能算法中引入其他優化思想，形成混合優化思想，可以有效地揚長避短，充分發揮智能算法的優點，大大提高算法的各方面性能[6]。

考慮到蟻群算法和遺傳算法在收斂性上的互補性，有多位學者陸續提出了基于蟻群算法和遺傳算法的混合優化算法[6]。這些混合算法通常采用固定進化代數來控制兩種算法的調用，很有可能造成已經早熟的種群還在進行無用的進化，影響算法的收斂速度。本文提出了一種基于目標函數變化率的混合蟻群遺傳算法，在進化過程中，根據目標函數的變化率動態地控制蟻群算法和遺傳算法的調用次數，并根據數值實驗結果對新算法的全局和局部收斂性進行了評測。

2 蟻群算法和遺傳算法

2.1 蟻群算法

用于優化領域的蟻群算法吸收了生物界中螞蟻群體的行為特征，其基本原理是：

（1）螞蟻能感知小范圍區域內的狀況，并判斷出是否有食物或其他同伴的信息素軌跡；

（2）螞蟻能連續不斷地釋放自己的信息素；

（3）螞蟻釋放的信息素濃度隨時間逐步減小。

螞蟻有能力在沒有任何提示下找到從其巢穴到食物的最短路徑，并且能隨環境的變化而變化，適應性地搜索新的路徑，產生新的選擇。其根本原因是螞蟻在尋找食物時，能在其走過的路上釋放信息素，隨著時間的推移該物質會逐漸揮發。當一定路徑上通過的螞蟻越來越多時，其留下的信息素也越來越多，后來的螞蟻選擇該路徑的概率也越高，從而更增加了該路徑的信息素強度。而強度大的信息素會吸引更多的螞蟻，從而形成一種正反饋機制。通過這種正反饋機制，螞蟻最終可以發現最短路徑。特別地，當螞蟻巢穴與食物間出現障礙物時，螞蟻不僅可以繞過障礙物，而且通過蟻群信息素在不同路徑上的變化，經過一段時間的正反饋，最終收斂到最短路徑。

蟻群算法在不同問題中有不同的表現形式，但其核心步驟均為信息素軌跡強度的更新方式和螞蟻轉移概率的確定。本文采用下列螞蟻圈模型[7]：

若路徑(i，j)在t時刻信息素軌跡強度為τij，螞蟻k在路徑(i，j)上留下的單位長度軌跡信息素數量為，軌跡的持久性為ρ(0≤ρ＜1)，則軌跡強度的更新方程為：

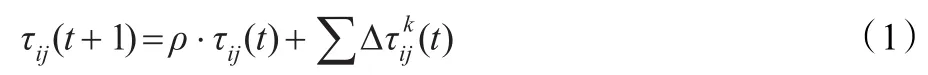
設Zk為第k只螞蟻在本次循環中所走的路徑的長度，則其中Q為一個常數。如果設ηij為路徑(i，j)的能見度，通常取為1/dij，dij為路徑(i，j)的長度，路徑可見度的相對重要性為β(β≥0)，路徑軌跡的相對重要性為α(α≥0)，U為可行頂點集，則螞蟻k在t時刻的轉移概率為：

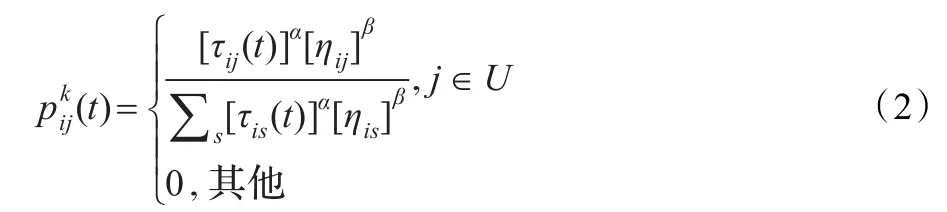
2.2 遺傳算法

遺傳算法的運算對象是由個體組成的群體。在遺傳算法的運算過程中，群體按照優勝劣汰的法則進行遺傳和進化，將適應度較高的個體更多地遺傳到下一代，經過若干代進化后，在群體中會得到一個或一批優良的個體，它們即對應問題的最優解。

生物的進化主要是通過染色體之間的交叉和染色體的變異來完成的。遺傳算法模擬這個進化過程，對群體使用遺傳算子，從而得出新一代群體。

基本遺傳算法的運算過程如下：

（1）選取適當的群體規模Μ、染色體編碼長度l、進化代數T、交叉概率Pc、變異概率Pm等參數，隨機生成規模為Μ的初始群體P(t)，t=0；

（2）解碼并計算適應度；

（3）進行選擇操作；

（4）進行交叉操作；

（5）進行變異操作，產生新一代種群P(t+1)；

（6）若t＜T，則t=t+1，轉（2），否則輸出最優解，停機。

3 混合蟻群遺傳算法

蟻群算法已被證明是一種很有發展前景的求解復雜優化問題（特別是離散優化問題）的有效方法。但與其他智能優化方法一樣，蟻群算法不可避免地存在著一些缺陷，如初始信息素生成速度較慢，全局收斂性較差，易早熟等。

近年來，許多學者將蟻群算法與其他優化算法相融合，相繼提出了多種混合蟻群算法，并將其應用于不同的領域，取得了較好的效果。劉波將分布估計思想引入蟻群算法[8]；陳立華和張瀟提出了含有變異算子的混合蟻群算法，并將其應用于水庫群優化[9-10]；梁亮將Markov過程與蟻群算法相結合[11]；周永務在蟻群算法中引入2-opt算法，并將其應用于多時間窗車輛路徑問題[12]；杜占瑋提出了基于互信息的混合蟻群算法[13]；稅薇提出了與人工勢場相結合的混合蟻群算法[14]；丁建立[15]提出采用遺傳算法生成信息素分布，利用螞蟻算法求精確解，優勢互補；毛寧[16]提出借助遺傳算法中的變異幫助蟻群算法提高跳出局部最優解的能力；梁旭[17]提出了一種動態蟻群混合遺傳算法，大大提高了蟻群算法的收斂速度。

本文提出一種基于目標函數變化率的動態混合蟻群遺傳算法（Dynamic Ant Colony Genetic Algorithm，DACGA），其基本思想是：根據目標函數的變化率交叉地調用蟻群算法和遺傳算法。用蟻群算法的解作為遺傳操作的種子，每當種群進化接近停滯時，調用蟻群算法。這種方法可動態地控制蟻群算法和遺傳算法的調用時機，再配合相應的信息素更新方法，可以提高算法的收斂性。

動態調用蟻群算法和遺傳算法的具體方法是：

定義：

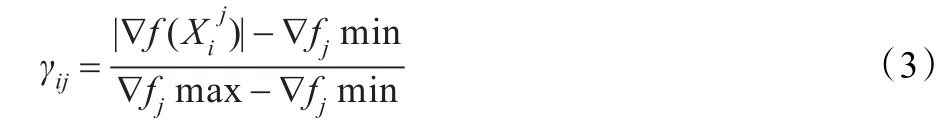
其中：

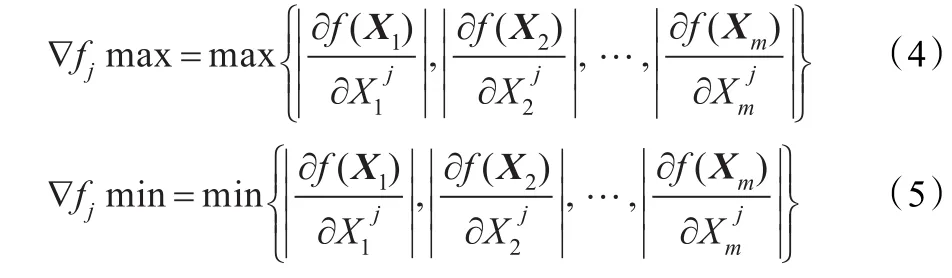
(i=1,2,…,m;j=1,2,…,n)表示向量Xi的第j個分量。

對于離散優化問題，f(X)不存在梯度，則

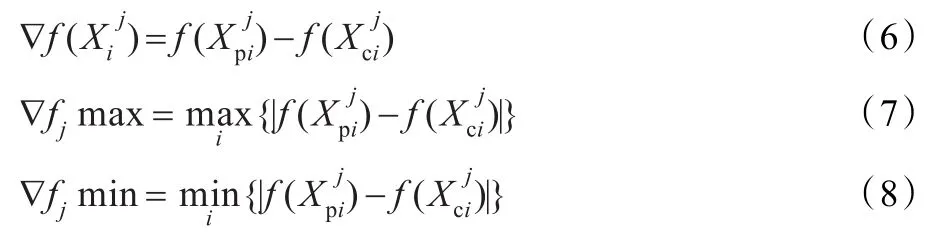
其中，Xp，Xc分別表示父代和子代個體。

當γij小于設定的閾值ε（通常取為10-2）時，選擇蟻群算法，否則選擇遺傳算法。

DACGA的流程如下：

（1）取定參數NGmin，NGmax，NKmax，α，β，ρ。

（2）螞蟻位置初始化。

（3）利用式（1）更新信息素，并轉（5），否則轉（4）。

（4）根據式（2）選擇下一節點。

（5）將螞蟻搜索到的初始解和全局最優解作為遺傳算法的初始種群，進行選擇、交叉、變異，更新種群。

（6）當遺傳算法達到最小迭代次數NGmin時，則根據前述方法動態選擇蟻群算法或遺傳算法。若選擇調用蟻群算法，則利用式（1）更新信息素，并轉（8）。

（7）當遺傳算法達到最大迭代次數NGmax時，則轉（8），否則繼續遺傳操作。

（8）若混合算法的整體迭代次數達到NKmax，則輸出最優解，算法結束，否則轉（2）。

4 算法的收斂性分析與性能評測

4.1 收斂性分析

混合蟻群遺傳算法的收斂性極為復雜，尚未完全解決。目前公認的結論是[18]：基于螞蟻圈模型的蟻群算法和基本遺傳算法的混合算法是收斂的。

由于本文采用的是基于螞蟻圈模型的蟻群算法和基本遺傳算法，只是對調用兩種算法的條件作了改進，所以本文提出的算法在理論上是收斂的。

4.2 性能評測

鑒于混合優化算法已被公認為解決車間調度問題較為有效的方法[19]，下面用基于目標函數變化率的DACGA算法對車間調度問題中的兩個基準測試問題FT06和FT10[19]進行仿真計算，并將計算結果與基本蟻群算法、基本遺傳算法和一種蟻群遺傳混合算法[16]（Ant Colony System Genetic Algorithm，ACSGA）的計算結果進行比較，從而檢驗新算法的收斂性能。

仿真程序采用Matlab編程，遺傳算法中，編碼長度為10，種群規模為50，交叉概率為0.85，變異概率為0.1，NGmin=20，NGmax=50；蟻群算法中，α=1，β=1，ρ=0.5，Q=800，NKmax=300；動態調用閾值ε=0.01。

考慮到計算結果的隨機性，表1和表2中給出的是20次實驗結果的平均值。

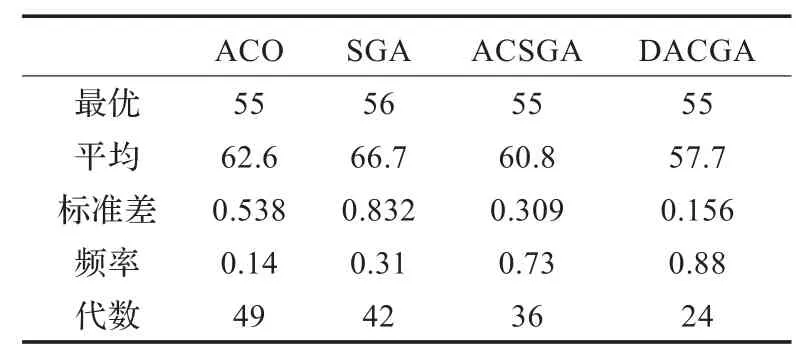
表1 FT06的優化指標結果

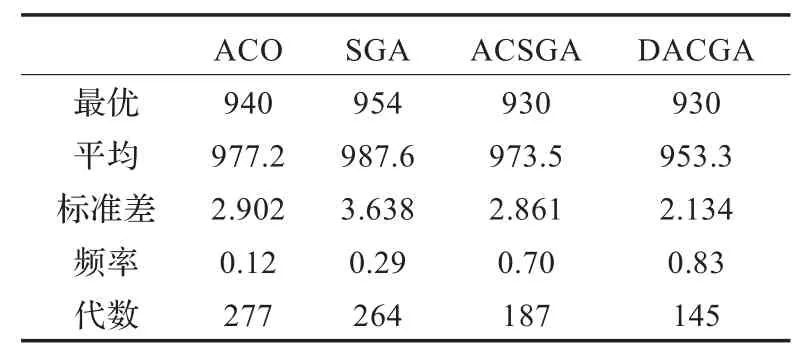
表2 FT10的優化指標結果

表1和表2中分別給出了FT06和FT10的最優值、平均值、標準差、20次仿真中求得最優值（達到理論最優解的95%即視為最優值）的頻率及最小進化代數。FT06和FT10的理論最優解分別為55和930。

為了更直觀地反映DACGA在收斂性方面的改進，圖1給出了DACGA與ACSGA求解FT10的對比進化曲線。

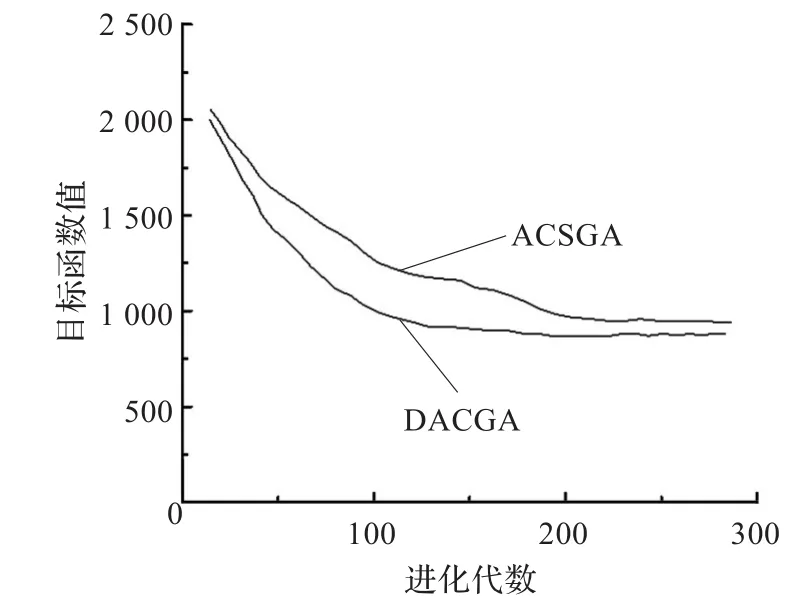
圖1 FT10的DACGA和ACSGA進化曲線

從表1、表2和圖1中可以很清楚地看出：

（1）ACO在最優值、平均值和標準差指標上優于SGA，而SGA在收斂頻率和進化代數指標方面優于ACO，即ACO局部收斂性較強而全局收斂性較弱，SGA全局收斂性較強而局部收斂性較弱。

（2）ACSGA和DACGA在所有指標中均較ACO和SGA為優，即混合蟻群遺傳算法的確可以優勢互補，提高收斂性。

（3）相比較而言，DACGA較ACSGA在收斂性和收斂速度方面又有一定程度的提高。這表明，本文提出的ACO和SGA的動態調用機制是有效的。

5 結束語

通過對蟻群算法和遺傳算法收斂性特點的分析，設計了一種基于目標函數變化率的算法調用機制，提出了一種新的混合蟻群遺傳算法。新算法不僅實現了蟻群算法和遺傳算法的優勢互補，而且通過動態調用兩種算法減少了冗余迭代次數，提高了收斂速度。數值仿真結果顯示，新算法與蟻群算法相比有較強的全局收斂性，而與遺傳算法相比則有較強的局部收斂性。

最后要特別指出的是，蟻群算法與粒子群算法、人工免疫系統、分布估計算法、協同進化算法等均為近年來出現的新型進化范例，理論體系尚不完善，收斂性等關鍵理論問題有待進一步研究。

[1]Dorigo M.Optimization，learning and natural algorithms[D]. Dipartimento di Elettronica，Politecnico di Milano，Italy，1992.

[2]Bonabeau E，Dorigo M，Theraulaz G.Inspiration for optimization from social insect behavior[J].Nature，2000，406（6）：39-42.

[3]Michael J B K，Jean-Bernarrd B，Laurent K.Ant-like task and recruitment in cooperation robots[J].Nature，2000，406（31）：992-995.

[4]Jackson D E，Holcombe M，Ratnieks F L W.Trail geometry gives polarity to ant foraging networks[J].Nature，2004，432（7019）：907-909.

[5]Holland J H.Adaptation in natural and artificial system[M]. Ann Arbor：The University of Michigan Press，1975.

[6]梁旭，黃明.現代智能優化混合算法及其應用[M].北京：電子工業出版社，2011.

[7]Dorigo M，Bonabeau E，Theraulaz G.Ant algorithms and stigmergy[J].Future Generation Computer System，2000，16（8）：851-871.

[8]劉波，李惠光，吳惕華，等.一種新的混合蟻群算法[J].數學的實踐與認識，2009，39（6）：154-161.

[9]陳立華，梅亞東，楊娜，等.混合蟻群算法在水庫群優化調度中的應用[J].武漢大學學報，2009，42（5）：661-665.

[10]張瀟，王江晴.混合蟻群算法在車輛路徑問題中的應用[J].計算機工程，2011，37（24）：190-192.

[11]梁亮，郭波.基于混合蟻群算法的產品開發過程優化方法[J].系統工程理論與實踐，2009，29（10）：118-128.

[12]彭碧濤，周永務.多時間窗車輛路徑問題的混合蟻群算法[J].計算機工程與應用，2010，46（31）：28-31.

[13]杜占瑋，楊永健，孫永雄，等.基于互信息的混合蟻群算法及其在旅行商問題上的應用[J].東南大學學報，2011，41（3）：478-481.

[14]稅薇，葛艷，韓玉，等.基于混合蟻群算法的無人機航路規劃系統[J].仿真學報，2011，23（3）：574-577.

[15]丁建立，陳增強，袁著祉.遺傳算法與螞蟻算法的融合[J].計算機研究與發展，2003，40（9）：1351-1356.

[16]毛寧，顧軍華.蟻群遺傳混合算法[J].計算機應用，2006，26（7）：1692-1694.

[17]梁旭，劉鵬飛，黃明.一種新的螞蟻遺傳混合算法應用研究[J].計算機集成制造系統，2008，14（8）：1566-1570.

[18]丁建立，陳增強，袁著祉.遺傳算法與螞蟻算法的融合的馬爾可夫收斂性分析[J].自動化學報，2004，30（4）：629-634.

[19]王凌.車間調度及其遺傳算法[M].北京：清華大學出版社，2003：58-59.

LIU Xuedong1,XU Feng2

1.School of Computer Science and Engineering,Anhui University of Science and Technology,Huainan,Anhui 232001,China
2.School of Science,Anhui University of Science and Technology,Huainan,Anhui 232001,China

According to the complementary on convergence of ant colony algorithm and genetic algorithm,a hybrid ant colony genetic algorithm based on the change rate of objective function is put forward.The basic idea of new algorithm is that the solutions of ant colony algorithm are given as the initial population of genetic algorithm,and the ant colony algorithm and genetic algorithm are dynamically called according to the change rate of objective function.When population evolutionary is close to stagnation, ant colony algorithm is called.This approach can dynamically control the call timing of ant colony algorithm and genetic algorithm. Together with the pheromone update methods,the convergence of hybrid algorithm is improved.The new algorithm is used to solve the Job shop scheduling benchmarks problem,and the simulation results show that the global and local convergence performance of new algorithm has been significantly improved compared with basic hybrid ant colony genetic algorithm.

Ant Colony Optimization（ACO）;Genetic Algorithm（GA）;change rate of objective function;Job shop scheduling benchmarks problem

根據蟻群算法和遺傳算法收斂性互補的特點，提出了一種基于目標函數變化率的混合蟻群遺傳算法。該算法的基本思想是：用蟻群算法的解作為遺傳算法的初始種群，根據目標函數的變化率交叉地調用蟻群算法和遺傳算法。每當種群進化接近停滯時，調用蟻群算法。這種方法可動態地控制蟻群算法和遺傳算法的調用時機，再配合相應的信息素更新方法，以提高算法的收斂性。將新算法用于車間調度基準測試問題，仿真結果表明，與常規混合蟻群遺傳算法相比，新算法的全局收斂性和局部收斂性有了明顯的提高。

蟻群算法；遺傳算法；目標函數變化率；車間調度基準問題

A

TP301.6

10.3778/j.issn.1002-8331.1210-0278

LIU Xuedong,XU Feng.Hybrid ant colony genetic algorithm based on change rate of objective function.Computer Engineering and Applications,2013,49（18）：41-44.

安徽省教育廳自然科學基金項目（No.2010kb236）。

劉雪東（1986—），男，碩士研究生，主要研究領域為進化計算、群智能計算；許峰（1963—），男，教授，主要研究領域為進化計算、群智能計算。E-mail：fxu@aust.edu.cn

2012-10-26

2013-01-30

1002-8331（2013）18-0041-04

CNKI出版日期：2013-03-19 http://www.cnki.net/kcms/detail/11.2127.TP.20130319.1424.001.html