融合鄰域粗糙集與粒子群優化的網絡入侵檢測

趙暉

陜西理工學院 數學與計算機科學學院，陜西 漢中 723000

融合鄰域粗糙集與粒子群優化的網絡入侵檢測

趙暉

陜西理工學院 數學與計算機科學學院，陜西 漢中 723000

1 引言

入侵檢測是一種通過收集和分析被保護系統信息來發現入侵的主動網絡安全技術，主要功能是對網絡和計算機系統進行實時監控，發現和識別系統中的入侵行為，發出入侵警報。入侵檢測一般被視為系統狀態是“正常”或“異常”的二分類問題。

入侵檢測領域中所獲得的數據具有非線性及高維特點，且數據往往并不服從某種已知分布，這就使得傳統統計學的方法難以進行有效的檢測，神經網絡、貝葉斯網絡、支持向量機以及K鄰近等機器學習方法被用于入侵檢測領域，其中支持向量機（Support Vector Machine，SVM）[1-4]是建立在統計學習理論基礎上，以結構風險最小化為準則的機器學習方法，具有結構簡單、全局優化、訓練時間短、泛化性能好等優點，較好地解決了高維、非線性、小樣本等問題。文獻[5-6]采用支持向量機進行入侵檢測，獲得了較好效果，顯示了支持向量機優于其他分類算法的性能。大量研究表明[7-8]，支持向量機性能與其核函數的類型、核函數參數和懲罰參數有著密切的關系，這些參數會影響SVM的分類精度及泛化性能。目前，人們往往憑經驗，通過大量反復實驗獲得較優參數，這種方法比較費時，獲得的參數不一定是最優的。近年，很多學者提出一些其他參數優化方法，文獻[9]利用梯度下降法進行參數優化，雖然縮短參數搜索時間，但對初始點的選取要求較高，且是一種線性搜索方法，極易陷入局部最優；文獻[10-11]利用遺傳算法、文獻[12-13]利用蟻群算法對SVM參數進行優化選擇，這些智能方法雖然降低了對初值選擇的依賴性，但算法原理和思想比較復雜，對不同的優化問題都需要設計不同的交叉、變異和選擇方式，且也易陷入局部最優。粒子群（ParticleSwarm Optimization，PSO）[14-15]算法是一種有效的全局尋優算法，通過種群中粒子之間的競爭與合作產生的群體智能來指導優化搜索過程尋找最優解，相對上述其他方法具有概念簡單、效率高及容易實現的特性。本文采用粒子群算法優化支持向量機的參數，以提高算法的泛化性能。

入侵檢測數據的屬性中并非所有屬性對入侵檢測都是有效或起決定性作用的，而且含有大量噪聲，同時屬性之間也存在一定的冗余，這會降低檢測精度，所以屬性約簡是提高入侵檢測性能的有效途徑。主成分分析、聚類、粗糙集、信息增益等是目前常用的屬性壓縮或約簡方法。粗糙集（Rough Set，RS）[16]是建立在離散空間等價關系上的專門研究不精確性和不確定性知識的數學工具，其核心是知識約簡，生成規則中包含了對分類起著不可或缺的條件屬性。蔡忠閩等[16-18]將粗糙集應用于入侵檢測，進一步提高檢測效果。但傳統粗糙集不能直接處理連續型數據，需要對連續屬性進行離散化，這一處理過程必然會帶來信息丟失，檢測結果受離散化處理技術的影響很大并且降低了檢測精度。鄰域粗糙集（Neighborhood Rough Set）[19-21]是一種在經典粗糙集理論基礎上發展起來的能夠直接處理連續型數據的方法，它不需要事先對連續數據進行離散化處理，在約簡之前不存在離散化帶來的信息損失問題，使選擇得到的屬性子集具有更強的分類能力。

基于以上分析，本文融合了鄰域粗糙集與粒子群進行入侵檢測。首先采用鄰域粗糙集方法對原始訓練集進行屬性約簡，消除噪聲及冗余屬性，然后再使用經粒子群優化核函數、懲罰等參數的支持向量機進行訓練與測試。本文并在KDD99數據集進行仿真實驗來驗證本文算法的有效性和優越性。

2 本文算法

2.1 基于鄰域粗糙集的屬性約簡

入侵檢測數據具有高維大樣本特征，這就使得機器學習過程中存在如下兩方面的問題：首先入侵檢測數據集中存在大量噪聲及冗余屬性，嚴重影響分類器的分類精度；其次，機器學習算法的訓練和分類時間隨數據維數的增加而增加，會降低分類算法的效率。大量研究證明，進行屬性約簡是提高分類器分類精度、提高算法效率的有效方法。

粗糙集理論[16]是由波蘭學者Pawlak于1982年提出的一種有效處理不完整、不精確信息的數學分析工具，該理論的特性是不需要任何先驗信息，僅使用數據本身的內部信息便能從中發現隱含知識，揭示潛在規律，對不完整不精確數據進行有效處理。傳統粗糙集理論首先要將連續數據離散化，這樣會導致原始信息的丟失，計算處理的結果在很大程度上取決于離散化的效果。鄰域粗糙集[19-21]是胡清華在經典粗糙集理論模型的基礎上發展起來的能夠直接處理連續型數據的方法，它不需要事先對連續型數據進行離散化處理，可直接用于知識約簡等問題。因此，為保證入侵檢測的準確性和原始信息的完整性，本文采用鄰域粗糙集方法進行屬性約簡，在此基礎上對入侵檢測信息樣本空間進行鄰域粒化，直接計算樣本距離，確定樣本之間相鄰關系。

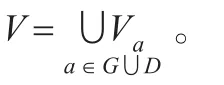
如果?si∈S且B∈G，樣本si在子屬性空間B中的鄰域記為δB(si)，則δB(si)={sj|sj∈S，ΔB(si，sj)≤δ}，其中δ是一個預設的閾值，ΔB(si，sj)是在子屬性空間B中的一個測度函數。通常使用的測度函數有：Manhattan距離、Euclidean距離和Chebychev距離。設s1和s2表示n維屬性空間G={g1，g2，…，gn}中的兩個樣本，f(s，gi)表示樣本s在第i維屬性gi的值，則Minkowsky距離可定義為：，當p=1，則稱之為Manhattan距離Δ1；p=2，則稱之為Euclidean距離 Δ2；p=∞，則稱之為Chebychev距離Δ∞。

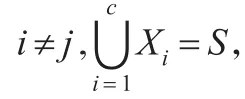
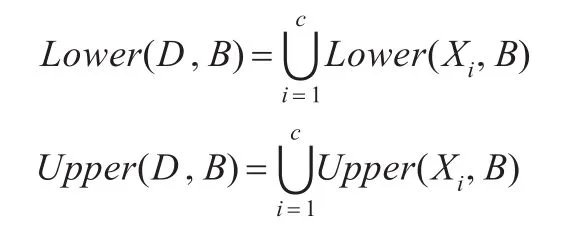
設a∈B，則屬性的重要度定義為：

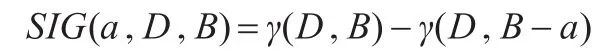
鄰域粗糙集屬性約簡算法：

算法結束

2.2 基于粒子群優化的支持向量機參數選擇

2.2.1 支持向量機

支持向量機[1-2]是一種基于統計學習理論的機器學習方法，以結構風險最小化為準則，較好地解決了高維、非線性、小樣本等問題。基本思想是基于Mercer定理，通過適當的非線性變換將輸入空間變換到一個高維特征空間，把在這個特征空間中尋找線性回歸最優超平面歸結為求解凸規劃問題，并求得全局最優解。

對于給定樣本點：

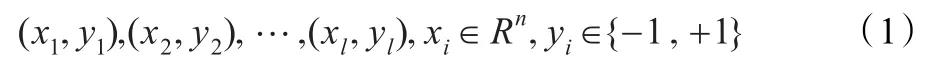
（1）線性可分。問題便歸結為以下優化問題

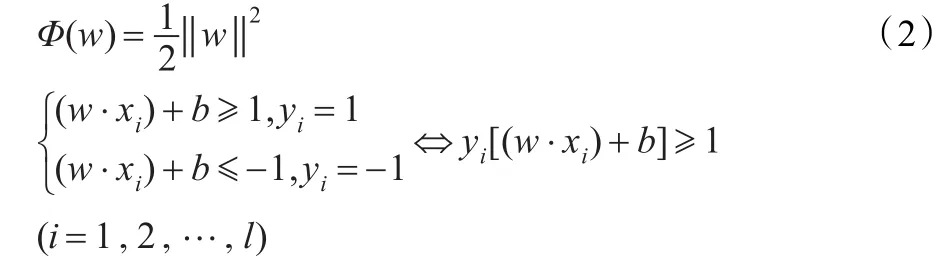
判別函數：

為了求解式（2），使用Wolfe對偶定理把上述問題轉化為其對偶問題進行求解：

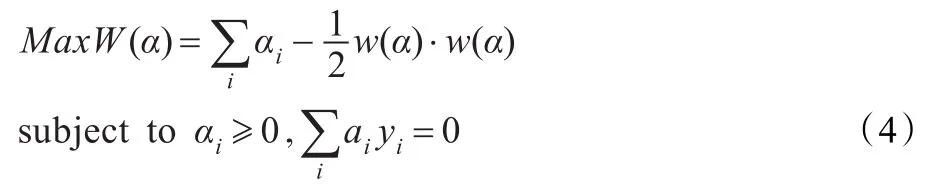
（2）線性不可分。引入松弛變量ξi，把式（2）改寫為下面的求解問題。

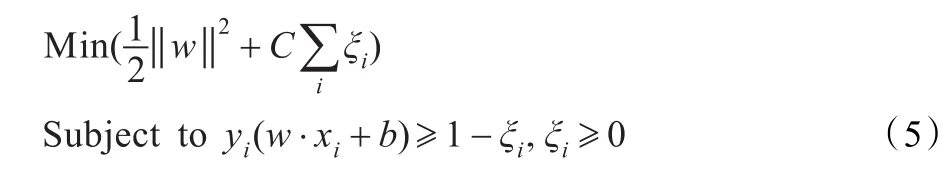
類似的可以得到相應的對偶問題：

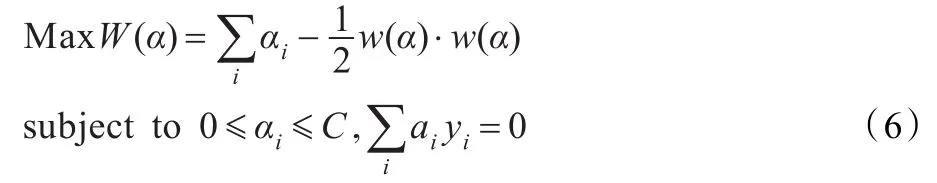
對式（4）、（6）的求解是一個典型的有約束的二次優化問題，已經有了很多成熟的求解算法。

2.2.2 粒子群算法

Eberhart于1995年提出了基于鳥群覓食行為的粒子群優化算法[14]，由于該算法概念簡明、實現方便、收斂速度快、參數設置少，是一種高效的優化算法。在粒子群算法中，每個個體稱為一個“粒子”，其實每個粒子代表著一個潛在的解。在一個D維的目標搜索空間中，每個粒子看成是空間內的一個點。設群體由m個粒子構成。m也被稱為群體規模，它的取值會影響算法的運算速度和收斂性。

PSO算法的數學描述為：設在一個D維空間中，由m個粒子組成的種群X=(x1，…，xi，…，xm)，其中第i個粒子位置為xi=(xi1，xi2，…，xiD)T，其速度為Vi=(vi1，vi2，…，vid，…，viD)T。它的個體極值為pibest=(pi1，pi2，…，piD)T，種群的全局極值為pgbest=(pg1，pg2，…，pgD)T，按照追隨當前最優例子的原理，粒子xi將按式（7）、（8）改變自己速度和位置。

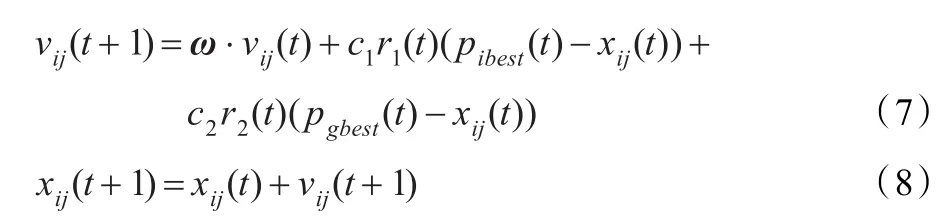
式中j=1，2，…，D，i=1，2，…，m，m為種群規模，t為當前進化代數，r1，r2為分布于[ ] 0，1之間的隨機數；c1，c2為加速因子，ω為權重向量。

2.2.3 基于粒子群算法的SVM參數優化算法

研究表明，支持向量機核函數及相關參數、懲罰參數是影響其分類性能的關鍵因素。其中，懲罰系數C反映了算法對離群樣本數據的懲罰程度，其值影響模型的復雜性和穩定性。C過小，對超出離群樣本點懲罰就小，訓練誤差變大；C過大，學習精度相應提高，但模型的泛化能力變差。C的值影響到對樣本中“離群點”（噪聲影響下非正常數據點）的處理，選取合適的C就能在一定程度提高抗干擾能力，從而保證模型的穩定性。

徑向基K(x，y)=exp(-‖x-y‖2/σ2)是應用最廣泛的核函數，無論是低維、高維、小樣本、大樣本等情況，RBF核函數均適用，具有較寬的收斂域，是較為理想的核函數。核函數的寬度系數σ反映了支持向量之間的相關程度。σ很小，支持向量間的聯系比較松弛，學習機器相對復雜，推廣能力得不到保證；σ太大，支持向量間的影響過強，難以達到足夠的精度。

因此核函數參數σ和懲罰參數C是影響支持向量機分類精度的重要因素。本文將采用粒子群算法搜索一組最優的懲罰系數、核參數{ }C，σ，使得支持向量機的分類精度最高。以支持向量機在訓練集上的交叉驗證誤差為適應度函數。算法具體步驟如下：

步驟1種群初始化與參數設置：種群粒子初始化{C，σ}，種群規模m，迭代次數T，加速因子c1，c2，權重因子ω。

步驟2計算初始粒子的適應度值并進行比較，取適應度最好的粒子（即適應度最小的粒子）所對應的個體極值作為最初的全局極值pgbest。

步驟3按照式（7）與式（8）進行迭代計算，更新粒子的位置、速度。

步驟4計算當前粒子的適應度。

步驟5將每個粒子的適應度值與其pibest對應的適應度值比較，若優，更新pibest，否則保留原值。

步驟6將更新后的每個粒子的pibest與全局極值pgbest比較，若優，更新pgbest，否則保留原值。

步驟7判斷是否滿足終止條件，若達到最大迭代次數T，或所得最優粒子不再變化就終止迭代，否則返回到步驟3。

2.3 本文算法的步驟與框架

步驟1利用鄰域粗糙集對訓練集進行屬性約簡，產生約簡的訓練集。

步驟2在產生的訓練集上利用粒子群算法優化支持向量機參數，獲得最優(C，σ)。

步驟3將(C，σ)作為支持向量機的參數，在約簡的訓練集上進行訓練，并在測試集上進行測試。

本文算法框架如圖1所示。

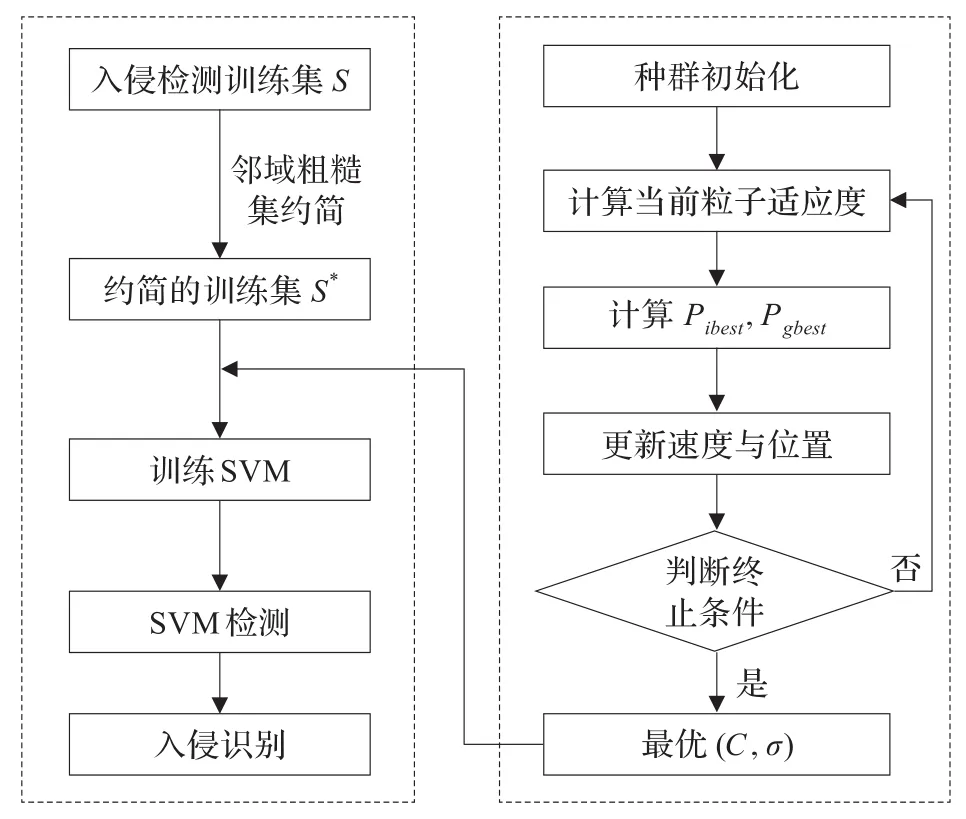
圖1 本文算法框架

3 仿真實驗及結果分析

3.1 實驗數據

選取KDD CUP 99數據集中的10%數據集作為實驗數據集。10%數據集包括訓練集和測試集兩部分，從10%數據集的訓練集中隨機抽取1 000個樣本作為訓練數據，其中包含入侵數據195個，其中包含四大類攻擊11種，具體為Dos攻擊有ueptne攻擊40個、smurf攻擊90個、back攻擊6個，probing攻擊有ipsweep攻擊10個、portsweep攻擊10個、satan攻擊15個，U2R攻擊有buffer_overflow攻擊4個、rootkit攻擊4個，R2L攻擊有waremster攻擊4個、Guess_passwd攻擊6個、warezclient攻擊6個。從10%數據集的訓練集中隨機抽取800個樣本分別作為測試數據，其中已知攻擊100個，為驗證算法對未知攻擊的檢測效果，加入未知攻擊100個。

為驗證本文算法對未知攻擊的檢測能力，在測試數據集中加訓練集中沒有的攻擊類型，分為4大類10種，分別為Dos攻擊有teardrop10個、pod20個、land5個，probing攻擊有nmap10個，U2R攻擊有loadmodule2個、perl2個，R2L攻擊有spy2個、phf2個、imap5個、multihop2個、ftp_write2個，測試集數據共包含攻擊類型21種。

3.2 算法評價標準

入侵檢測系統的性能評價指標主要有兩個：檢測率、誤警率。

3.3 實驗方法

為了研究算法的穩定性，實驗重復100次，取其平均值作為實驗結果。其中：

算法1：直接采用SVM進行分類（該算法中SVM參數隨機生成）。

算法2：先采用粗糙集進行屬性約簡，然后利用SVM進行分類（算法中SVM參數隨機生成）。

算法3：先采用鄰域粗糙集進行屬性約簡，然后利用SVM分類（該算法中SVM參數隨機生成）。

本文算法：先用鄰域粗糙集進行屬性約簡，然后使用PSO優化SVM參數，最后利用SVM分類。

3.4 實驗結果與分析

3.4.1 鄰域粗糙集半徑與入侵檢測精度

在算法3與本文算法中，需要設置鄰域粗糙集的半徑，半徑的不同會導致分類精度的差異，這里設置鄰域半徑在0.01到1之間，以0.01為步長的方式取值，對于鄰域半徑每一個取值，算法都得到一個屬性子集，共獲得100個屬性子集。

圖2、3分別直觀地顯示了入侵檢測率、誤警率與鄰域半徑之間的關系。從圖2可以看出半徑在0.01到0.24之間的時候，其入侵檢測率保持在81%左右，而當半徑增加到0.27到0.48之間時，檢測率有大幅提高，大概在92%左右，說明鄰域半徑對檢測率的影響是較大的。從圖3看到，半徑在0.01到0.48之間的時候，其誤警率基本保持在2%左右，而0.48到0.6，誤警率大幅增加。

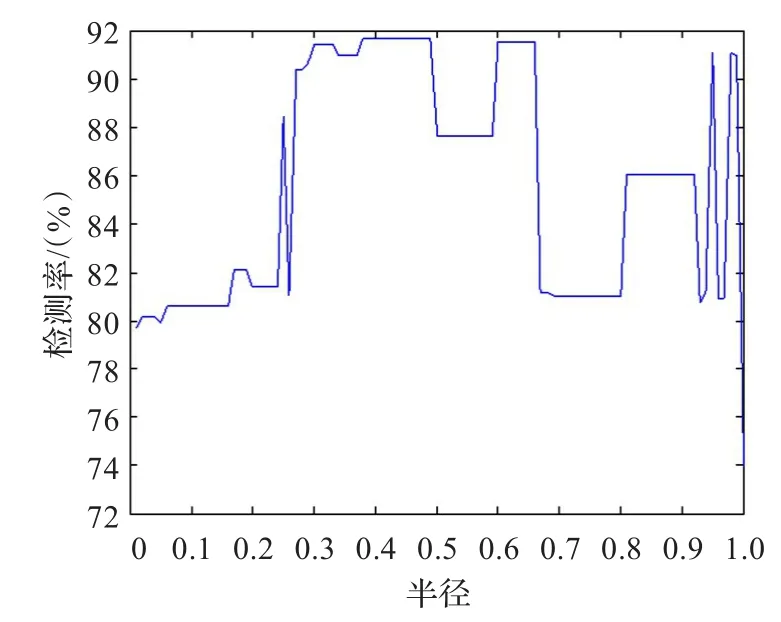
圖2 鄰域粗糙集半徑與入侵檢測率關系

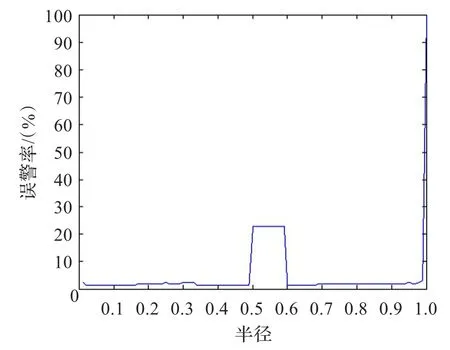
圖3 鄰域粗糙集半徑與入侵誤警率關系

綜合以上分析可得，當鄰域半徑在0.3到0.48與0.6到0.66之間的時候，其檢測率較高，同時誤警率達到較低的狀態，這為鄰域粗糙集的使用提供一定借鑒。

3.4.2 不同算法的檢測精度比較

粒子群算法中的參數設置如下：c1為1.5，c2為1.7，最大進化代數為200，種群規模為20，k為0.6，速率更新公式中速度前面的彈性系數為1，種群更新公式中速度前面的彈性系數為1，SVM Cross Validation參數為3，SVM參數c的變化范圍為[0.1，100]，SVM參數δ的變化范圍為[0.01，1 000]。

表1 算法1、算法2、算法3與本文算法的實驗結果 （%）

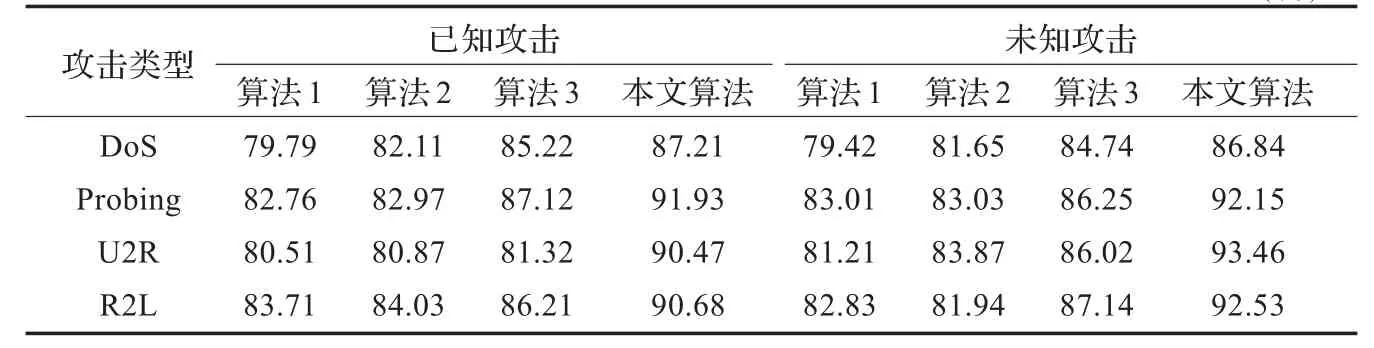
表2 不同算法對已知、未知攻擊的平均檢測率 （%）

表1給出了四種不同算法的實驗結果。可以看到，本文算法的檢測率平均值與最優值是四種算法中最高的，同時誤警率是最低的。算法2采用了粗糙集對數據集進行了屬性約簡，使得檢測率相對算法1提高約3%左右，說明通過屬性約簡可以剔除部分噪聲和冗余屬性，提高入侵檢測效果；算法3檢測率相對算法2提高約4%左右，說明了鄰域粗糙集直接對連續型數據進行處理，避免傳統粗糙集離散化過程中帶來的信息損失，入侵檢測效果進一步提高；當SVM參數C=1.47，σ=4.09，鄰域粗糙集半徑取0.31，本文算法的入侵檢測率最優值達到95.42%，誤警率到達0.81%，其檢測性能優于其他算法，主要是SVM參數的選擇對于增強分類器的泛化性能具有很大的影響，最終導致檢測性能的大幅提高。

表2給出四種算法在已知、未知攻擊上的檢測率。發現本文算法對已知攻擊和未知攻擊檢測上都有大幅度的提高，充分說明了該算法對未知攻擊檢測的有效性，算法具有較強的泛化性能和魯棒性。

3.4.3 穩定性分析

圖4顯示了四種不同算法的穩定性。可以清楚地看出本文算法在穩定性以及精確率兩方面都遠優于其他算法，具有更好的泛化性能和魯棒性。

圖4 四種不同算法的穩定性與精度比較

4 結論

入侵檢測數據往往具有噪聲和冗余屬性，并且部分屬性數據具有連續性，為了克服連續屬性離散化過程中帶來的信息損失，本文采用鄰域粗糙集模型進行屬性約簡，并使用粒子群算法優化支持向量機核函數參數和懲罰參數，在KDD99數據集上的仿真實驗結果表明本文算法可以進一步提高入侵檢測率并同時降低誤警率，該算法具有較強的泛化性能和魯棒性。

[1]Sanchez A D.Advanced support vector machines and kernel methods[J].Neurocomputing.2003，55（1）：15-20.

[2]陳濤.選擇性支持向量機集成算法[J].計算機工程與設計，2011（5）：259-263.

[3]陳濤.基于雙重擾動的支持向量機集成[J].計算機應用，2011，28（1）：46-49.

[4]陳濤.基于加速遺傳算法的選擇性支持向量機集成[J].計算機應用研究，2011，32（2）：57-61.

[5]陳光英，張千里，李星，等.基于SVM分類機的入侵檢測系統[J].通信學報，2002，23（5）：51-56.

[6]饒鮮，董春曦，楊紹全，等.基于支持向量機的入侵檢測系統[J].軟件學報，2003，14（4）：798-803.

[7]陳濤.基于差分進化算法的支持向量回歸機參數優化[J].計算機仿真，2011（6）：674-679.

[8]陳濤，雍龍泉，鄧方安，等.基于差分進化算法的支持向量機參數選擇[J].計算機工程與應用，2011，47（5）：24-26.

[9]Chappelle O.Choosing multiple parameters for support vector machines[J].Machine Learning，2002，46（1）：131-160.

[10]Zheng Chunhong，Jiao Licheng.Automatic parameters selection for SVM based on GA[C]//Proceedings of the 5th World Congress on Intelligent Control and Automation.Piscataway，NJ：IEEE Press，2004：1869-1872.

[11]楊潔.基于遺傳算法的SVM帶權特征和模型參數優化[J].計算機仿真，2008（9）：48-51.

[12]齊亮.基于蟻群算法的支持向量機參數選擇方法研究[J].系統仿真技術，2008（11）：34-38.

[13]秦軍立，倪世宏，蘇晨.基于蟻群優化SVM及其應用研究[J].計算機仿真，2009（11）：46-49.

[14]Fukuyama Y.Fundamentals of particle swarm optimization techniques[M]//Modern Heuristic Optimization Techniques：Theory and Applications to Power Systems.[S.l.]：IEEE Power Engineering Society，2002：45-51.

[15]Shao Xinguang，Yang Huizhong，Chen Gang.Parameters selection and application of support vector machines based on particle swarm optimization algorithm[J].Control Theory and Applications，2006，23（5）：740-743.

[16]張義榮，鮮明，肖順平，等.一種基于粗糙集屬性約簡的支持向量異常入侵檢測方法[J].計算機科學，2006，33（6）：64-68.

[17]趙曦濱，井然哲，顧明，等.基于粗糙集的自適應入侵檢測算法[J].清華大學學報，2008，48（7）：1158-1168.

[18]陳濤.基于動態粗糙集約簡的選擇性支持向量機集成[J].計算機仿真，2012，43（2）：328-331.

[19]胡清華，于達仁，謝宗霞，等.基于鄰域粒化和粗糙逼近的數值屬性約簡[J].軟件學報，2008，15（3）：121-125.

[20]胡清華，趙輝，于達仁，等.基于鄰域粗糙集的符號與數值屬性快速約簡算法[J].模式識別與人工智能，2008，21（6）：89-95.

[21]Hu Q H，Yu D R，Liu J F，et al.Neighborhood rough set based heterogeneous feature subset selection[J].Information Sciences，2008，178（18）：3577-3594.

ZHAO Hui

School of Mathematics and Computer Science,Shaanxi University of Technology,Hanzhong,Shaanxi 723000,China

The intrusion detection data contains large redundant and noisy features,as well as some continuous attributes.This paper presents an algorithm based on neighborhood rough set and Particle Swarm Optimization algorithm for the effect of intrusion detection.Training subset is reduced by using neighborhood rough set,and new training subset is generated.The redundant attributes and noise are eliminated to avoid information loss when using traditional rough set;parameters of Support Vector Machine are optimized using particle swarm algorithm to avoid the risk of low precision by subjective choiced parameters.It improves the performance of the intrusion detection.The simulation results in the KDD99 dataset show that the algorithm can effectively improve the accuracy and efficiency of intrusion detection.It has high generalization and stability.

network intrusion detection;neighborhood rough set;Support Vector Machine（SVM）;Particle Swarm Optimization（PSO）algorithm

入侵檢測數據往往含有大量的冗余、噪音特征及部分連續型屬性，為了提高網絡入侵檢測的效果，利用鄰域粗糙集對入侵檢測數據集進行屬性約簡，消除冗余屬性及噪聲，也避免了傳統粗糙集在連續型屬性離散化過程中帶來的信息損失；使用粒子群算法優化支持向量機的核函數參數和懲罰參數，以避免靠主觀選擇參數帶來精度較低的風險，進一步提高入侵檢測的性能。仿真實驗結果表明，該算法能有效提高入侵檢測的精度，具有較高的泛化性和穩定性。

入侵檢測；鄰域粗糙集；支持向量機；粒子群算法

A

TP18

10.3778/j.issn.1002-8331.1301-0383

ZHAO Hui.Network intrusion detection algorithm based on neighborhood rough set and PSO.Computer Engineering and Applications,2013,49（18）：73-77.

國家自然科學基金（No.81160183）；陜西省教育廳科研基金（No.12JK0864）；陜西理工學院科研基金（No.SLGKY11-08）。

趙暉（1979—），男，講師，研究方向為數據挖掘、網絡安全。E-mail：zh911@sina.com

2013-02-01

2013-03-18

1002-8331（2013）18-0073-05

CNKI出版日期：2013-04-08 http://www.cnki.net/kcms/detail/11.2127.TP.20130408.1646.001.html