網側PWM整流器LCL輸出濾波器優化設計

黃輝先，徐榮

湘潭大學 信息工程學院，湖南 湘潭 411105

網側PWM整流器LCL輸出濾波器優化設計

黃輝先，徐榮

湘潭大學 信息工程學院，湖南 湘潭 411105

1 引言

PWM整流器廣泛應用于新能源發電、高壓直流輸電、有源電力濾波器和靜止無功補償等領域。由于整流器在采用PWM調制時，功率開關器件的高通斷頻率會產生高次諧波，為消除諧波污染，需要在電網和整流器之間加入濾波裝置[1]。

傳統方法是采用L濾波器抑制高次諧波。但隨著整流器功率等級的提高，L濾波器逐漸暴露出體積過大、成本過高，以及導致系統動態性能降低等一系列問題[2]。文獻[3]率先提出了采用LCL濾波器代替L濾波器來解決上述難題。近年來，不少研究討論了LCL濾波器設計的問題。文獻[1]定性研究了LCL濾波器的設計，給出了一些約束條件和設計步驟。文獻[4]提出了一種經驗取值法，可以快速得到參數值，但未考慮系統穩定性的影響。文獻[5]提出的構造有關諧振頻率、諧波衰減比、濾波電容和總電感的一元二次方程法，一定程度上簡化了參數設計的過程，但方程推導出發點基于約等于情況，并且電感比值的確定需要多次試值。文獻[6]提出利用調制方式產生的諧波電壓幅值進行迭代運算法，思路簡單，但算法復雜，不易工程實現。文獻[7]提出了基于遺傳算法的LCL濾波器設計方法，能夠搜尋最優值，但未詳細考慮對系統動態性能的影響。

本文結合傳統的LCL濾波器設計方法，推導出與文獻[5]不同且與電感比有關聯的諧波衰減比等式，結合圖形分析取值，能更簡便快速地得到參數值。文中詳細闡述了該方法的設計過程，并給出了實例設計及仿真對比結果。

2 LCL濾波器分析

2.1 LCL濾波器傳遞函數

LCL濾波的網側PWM整流器拓撲圖，如圖1所示，其中，T1到T6為IGBT，Lg為網側電感，Lr為整流器側電感，Cf為濾波電容，Rg、Rr為電感等效電阻，Rd為抑制LCL濾波器諧振而設的阻尼電阻，C為整流器直流側電容，Udc為整流器直流側電壓，ex為電網各相電壓，ux為整流器交流側輸出各相電壓，igx為網側各相相電流，irx為整流器側各相相電流，icx為濾波器電容各支路相電流(x=a，b，c)，參考方向如圖1所示。

因LCL濾波器三相對稱，故取一相分析，如圖2所示。

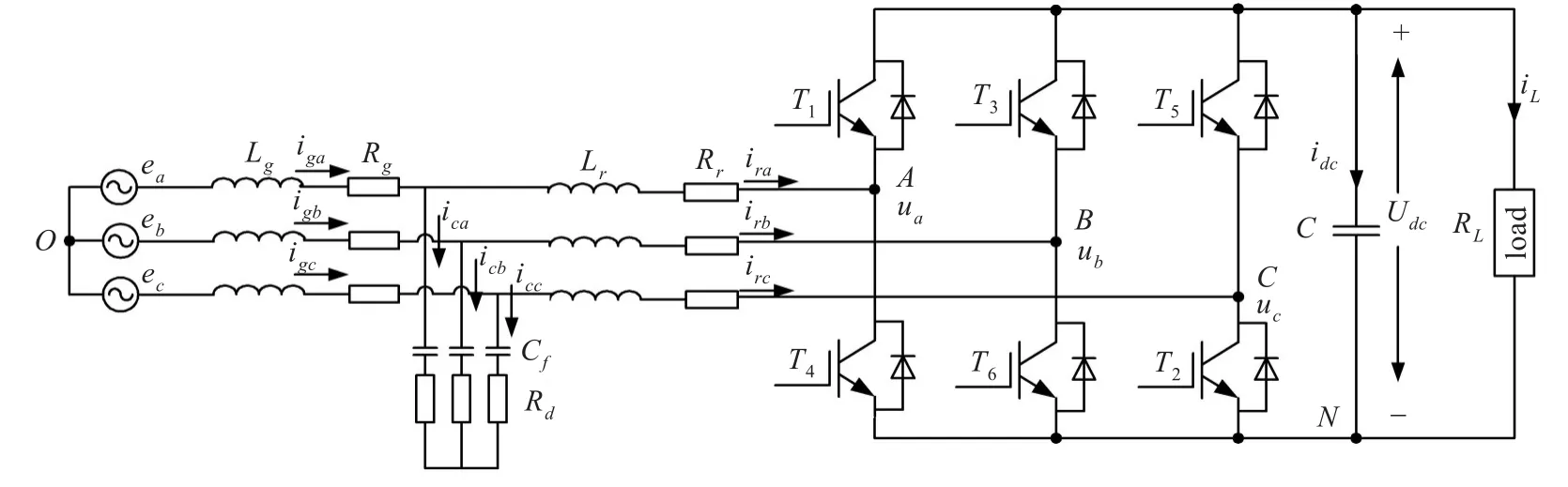
圖1 LCL濾波的網側PWM整流器拓撲圖

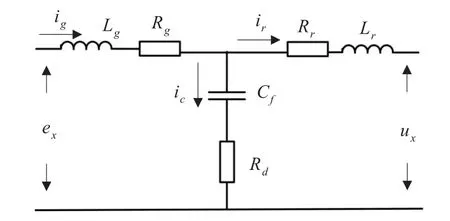
圖2 LCL濾波器單相等效圖

假設理想電源諧波含量為0，由此建立傳遞函數可得：

由勞斯穩定判據可知該二端口網絡不穩定。在某一頻率處，系統阻抗為0，其諧振頻率為（令Lg=rLr，L=Lg+Lr）：

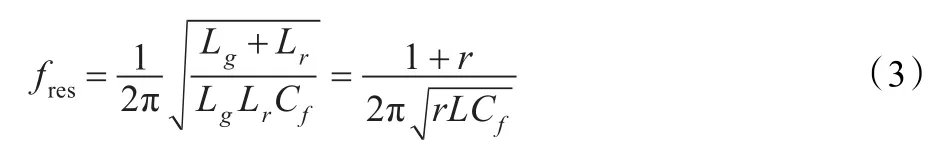
然而實際電感電容中存在著等效阻抗，其值很小，對系統的穩定性影響很小。為解決系統穩定性問題，文獻[8]詳細探討了在LCL各處串聯電阻時系統穩定性的情況，綜合串聯電阻臨界值和比例系數臨界值方面考慮，得出電容處串聯電阻最優。在濾波電容處串聯電阻的方法稱為無源阻尼法，在工程應用中電阻值一般取諧振點容抗的1/3左右，即Rd=1/(3Cfωres)。

由圖2所示的二端口網絡亦可求得：

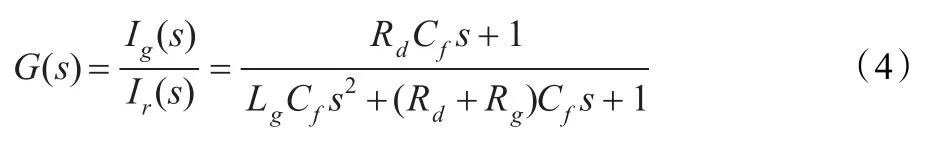
因PWM整流器交流側輸出電壓諧波主要分布在開關頻率附近[6]，故在開關頻率處G(s)的幅值和相位表達式有：

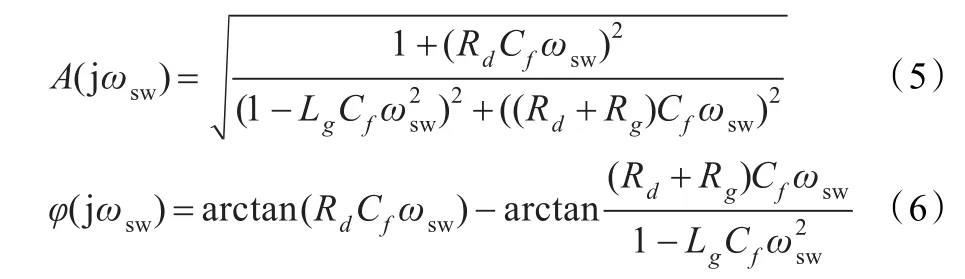
忽略Rd、Rg的影響，代入Lg=rL/(1+r)，式（5）可等效為：

d為諧波電流幅值衰減比。令ωres=kωsw(k∈(0，0.5))，由式（3）可得==(1+r)2/(k2r)，代入（7）中可求得：

與文獻[5]所推導出的一元二次方程相比，簡化了計算，解決了試值求解方程的缺點。

2.2 LCL濾波器參數選取原則

2.2.1 總電感選取原則

通過分析LCL濾波器與L濾波器的頻率特性曲線，二者在低頻段曲線幾乎重合，因此其總電感值可以按L濾波器的思路設計，其約束不等式有[9]：

通常歸納的總電感取值約束不等式有[5]：

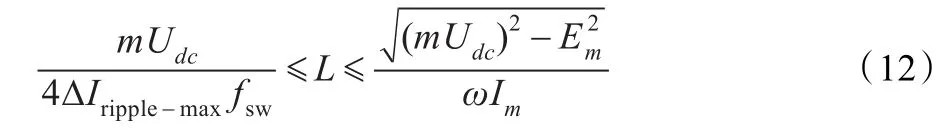
式中m為PWM調制比，SPWM取0.5，SVPWM取0.577；Em為電網相電壓峰值，Im為交流側基波相電流峰值，ΔIripple-max為最大允許諧波電流脈動量（一般可取15%到25%），Udc為整流器直流側電壓，ω為基波角頻率，Ts為PWM開關周期。在總電感設計過程中，結合式（11）和（12），根據最小電感優化準則，從最小值開始選取。

2.2.2 濾波電容選取原則

濾波電容吸收的無功功率不能超過系統額定功率的5%，文獻[1]給出了計算電容的約束不等式為Cf＜5%Cb。文獻[6]從忽略網側電感對輸出功率因數的影響角度出發，提出了Cf≈P sinφ/(3ω)。然而過大的Cf會顯著降低系統的功率因數；太小的Cf需增大網側電感，才能達到電流諧波衰減標準[10]。由式（3）可得Cf=(1+r)2/((2πfres)2rL)，當r和L取某值時，Cf與fres成反比，而諧振頻率有約束等式：

式中，f為電網基波頻率。通過對fres與r的關系圖分析可知，曲線中fres最小值與Cf存在一定關系，可得Cf的約束條件為：

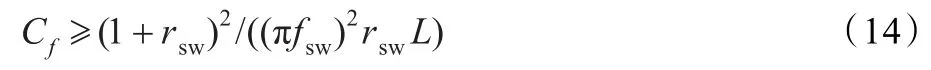
式中，rsw為fres最小值剛好落在0.5fsw處的值。

3 實例設計

在設計LCL濾波器之前，給出網側PWM整流器系統參數：系統額定功率為10 kW，電網相電壓有效值為220 V，電網基波頻率為50 Hz，直流側參考電壓為600 V，直流側電容為4 700 μF，開關頻率為2 kHz，采用SVPWM調制方式，負載為50 Ω。

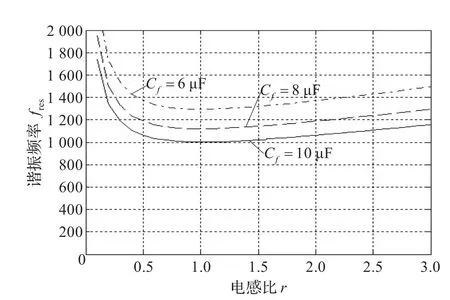
圖3 Cf為6 μF、8 μF、10 μF時fres與r的關系圖

（1）總電感設計

取ΔIripple-max=20%Im，系統參數代入式（11）、（12）有：10.1 mH≤L≤22.6 mH和8.1 mH≤L≤59.4 mH，綜合可得10.1 mH≤L≤22.6 mH。選取L=10.1 mH。

（2）濾波電容設計

根據選取原則計算可得Cf＜10.96 μF，若取sinφ=0.03，Cf≈6.58 μF。當L=10.1 mH時，代入式（3），不同Cf時fres與r的關系圖，如圖3所示。

由圖3可知，當L一定時，Cf增加到某值以后，fres最小值才會落在式（13）范圍內，故可以確定此處為Cf的下限值。在r=1處，fres有最小值且fres=0.5fsw，代入式（14）可得Cf≥10.03 μF。選取Cf=10.05 μF。

（3）電感比r設計

將步驟（1）、（2）所設計的參數值代入式（3）、（7）得到具體表達式，其關系圖如圖4所示。

由圖4可知，r在某一范圍內，d的變化受其影響很小，綜合考慮步驟（2）的情況，取r=1，此時d=0.14。因此可得Lg=Lr=5.05 mH，Cf=10.05 μF，計算所需阻尼電阻Rd=5.28 Ω。

4 系統仿真

系統仿真模型采用電網電壓定向矢量控制策略，控制框圖如圖5所示。控制器設計采用雙環控制，即電壓外環與電流內環。外環的作用是控制整流器直流側電壓，內環按電壓外環輸出的電流指令進行電流控制，實現有功電流和無功電流的獨立控制[9]。

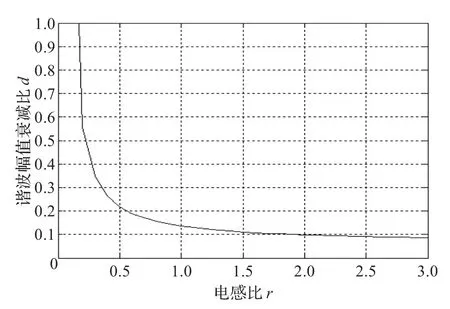
圖4 d與r的關系圖

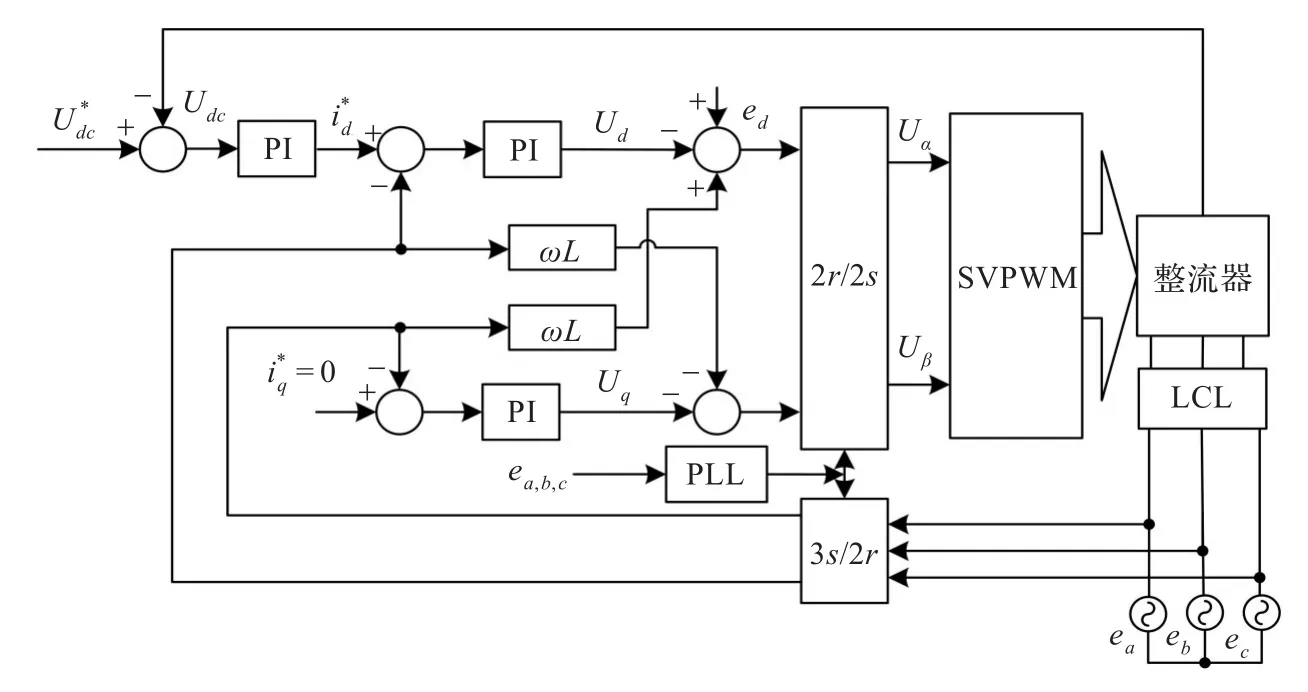
圖5 基于電網電壓定向矢量控制系統框圖

為比較不同設計方法下的濾波效果，將所設計的參數代入仿真模型。根據文獻[4]的經驗取值法得Lg=3.5 mH，Lr=7 mH，Cf=10.88 μF，為保證系統穩定性，仿真時加入阻尼電阻Rd=4.88 Ω；根據文獻[5]得Lg=10.2 mH，Lr=7.8 mH，Cf=6.58 μF，Rd=8.64 Ω。其網側輸入電流波形及諧波頻率分析圖、直流電壓輸出波形，如圖6、圖7、圖8所示。

由圖可知，總電感值越大，THD值越小，但系統的動態性能會變差，因此參數的設計需要綜合考慮。本文提出的方法能夠在總電感值最小時，使THD值最小，系統動態性能達到要求。

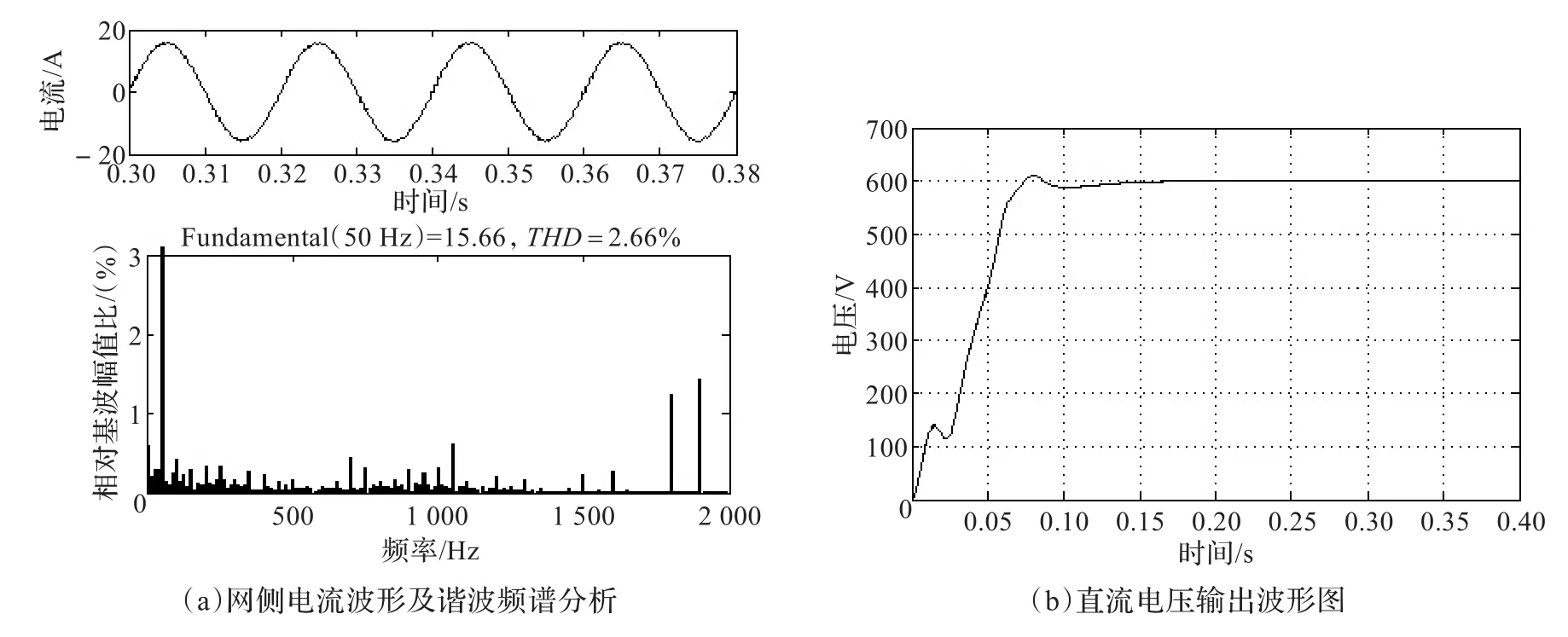
圖6 經驗取值法

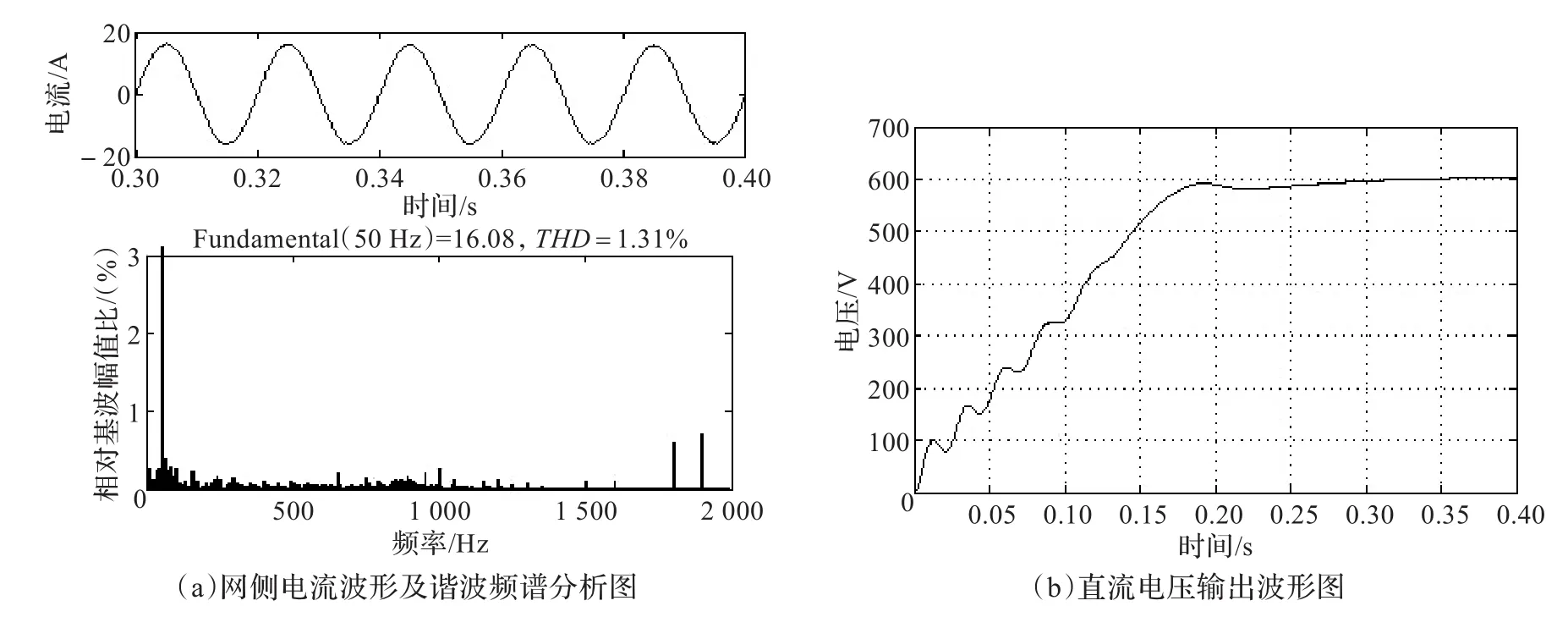
圖7 構造一元二次方程法

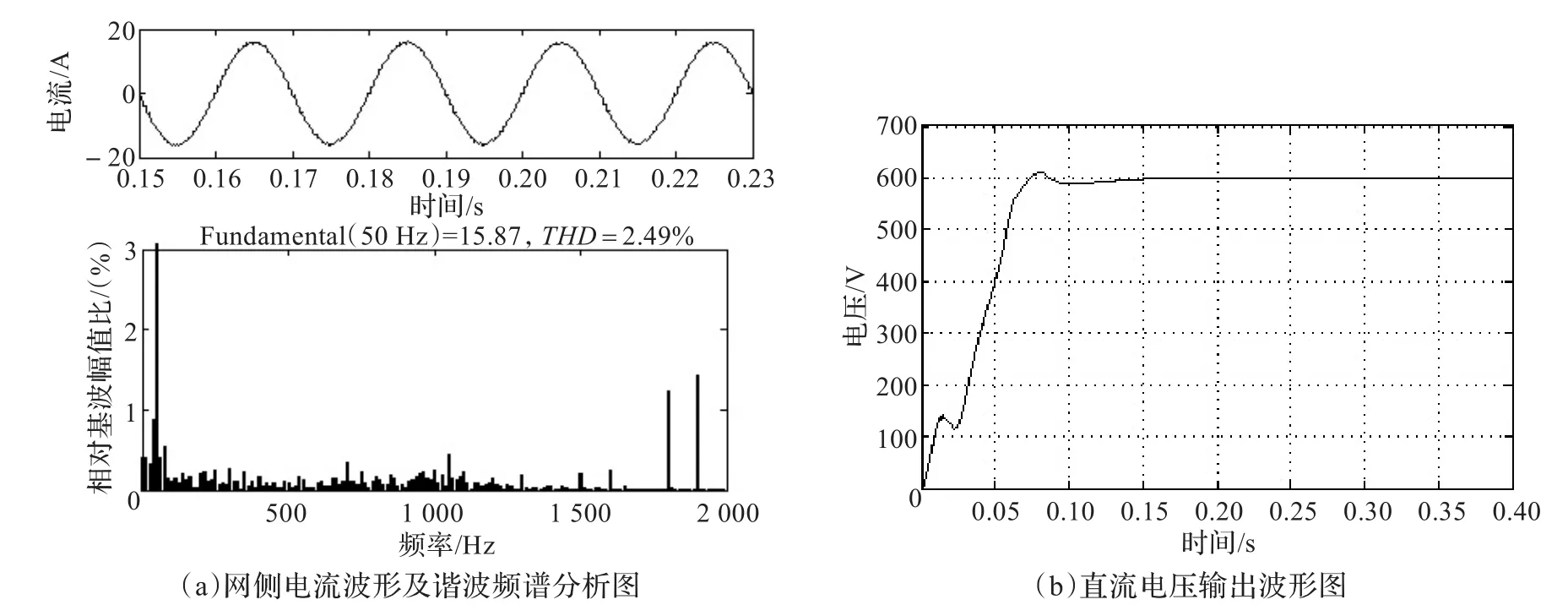
圖8 構造一元一次方程及圖形分析法

5 結束語

（1）對LCL濾波器建模分析表明，其總電感、濾波電容受諧振頻率的影響較大；在無功功率限制范圍內，總電感一定時，隨著濾波電容增大，THD值減小，所需阻尼電阻亦減小，但系統動態性能會降低。

（2）仿真結果表明：經驗取值法能快速決定參數值，但濾波效果不一定最好；一元二次方程法通過改變總電感值解方程獲得正的電感比值，費時且所選參數值不是最優；本文提出的設計方法能結合二者的優點，從而獲得更優的參數值。

[1]Liserre M，Blaabjerg F，Hansen S.Design and control of an LCL-filter based three-phase active rectifier[J].IEEE Transactions on Industry Applications，2005，41（5）：1281-1291.

[2]Liserre M，Dell’Aquila A，Blaabjerg F.Stability Improvements ofanLCL-filterbasedthree-phaseactiverectifier[C]// Proceedings of the 33rd Annual Conference on Power Electronics Specialists，2002：1195-1201.

[3]Lindgren M，Svensson J.Connecting fast switching vlotagesource converters to the grid-harmonic distortion and its reduction[C]//Proceedings of the IEEE Strock Power Tech Conference，Stockholm，Sweden，1995：191-195.

[4]何良，趙繼敏，謝海先.三相電壓型脈寬調制整流器的LCL濾波器設計[J].電網技術，2006，30：51-53．

[5]張憲平，李亞西.三相電壓型PWM整流器的LCL濾波器分析與設計[J].電氣應用，2007，26（5）：65-68.

[6]郭希錚，游小杰，張立偉，等.三相電壓型PWM整流器LCL濾波器設計方法[J].電力電子，2010，6（3）：33-38.

[7]武健，馬驍，侯睿，等.基于遺傳算法的有源濾波器LCL輸出濾波器優化設計[J].電工技術學報，2011，26（5）：159-164.

[8]郭小強，鄔偉揚，顧和榮，等.并網逆變器LCL接口直接輸出電流控制建模及穩定性分析[J].電工技術學報，2010，25（3）：102-109.

[9]張崇巍，張興.PWM整流器及其控制[M].北京：機械工業出版社，2003：133-148.

[10]黃宇淇，姜新建，邱阿瑞.LCL濾波器在三相PWM整流器中的應用[J].電力自動化設備，2008，28（12）：110-113.

HUANG Huixian,XU Rong

College of Information Engineering,Xiangtan University,Xiangtan,Hunan 411105,China

This paper proposes a design method for an LCL filter in grid-side PWM rectifier,then it is modeled.The research in single-phase model transfer function of LCL filter is made to obtain the relation between resonance frequency,harmonic current amplitude attenuation factor and factor r—the ratio between grid-side and rectifier-side inductance.The total inductance,capacitance of filter and r can be selected by analyzing the change tendency of the variable relation figures.The analysis results indicate that the lower limit of the total inductance and capacitance of filter are determined by resonance frequency.Finally,a designed example is reported,and the validity of this method is tested by simulation.

PWM rectifier;LCL filter;parameters design

提出一種網側PWM整流器LCL濾波器的參數設計方法，通過對LCL濾波器單相模型傳遞函數的研究，得到諧振頻率、諧波電流幅值衰減比與r（網側電感與整流器側電感的比例因子）之間的關系式。利用關系式分析各變量的變化規律，確定總電感值、濾波電容值和r。分析結果表明，諧振頻率可確定總電感和濾波電容的下限值。給出了一個設計實例，進行系統建模仿真驗證。仿真對比結果證明了該設計方法的正確性和優越性。

PWM整流器；LCL濾波器；參數設計

A

TP39

10.3778/j.issn.1002-8331.1202-0211

HUANG Huixian,XU Rong.Optimized design of LCL output filter for grid-side PWM rectifier.Computer Engineering and Applications,2013,49（13）：253-257.

湖南省自然科學基金委員會與湘潭市政府自然科學聯合基金（No.10JJ9008）。

黃輝先（1957—），男，教授，博導，主要研究領域為先進控制理論及應用，非線性控制理論；徐榮（1984—），男，碩士，主要研究領域為先進控制理論及應用。E-mail：bear15888@163.com

2012-02-13

2012-03-30

1002-8331（2013）13-0253-05

CNKI出版日期：2012-06-15http://www.cnki.net/kcms/detail/11.2127.TP.20120615.1726.039.html