一種新型的移動機器人軌跡跟蹤控制方法

張揚名，劉國榮，2

1.湘潭大學 信息工程學院，湖南 湘潭 411105

2.湖南工程學院，湖南 湘潭 411101

一種新型的移動機器人軌跡跟蹤控制方法

張揚名1，劉國榮1，2

1.湘潭大學 信息工程學院，湖南 湘潭 411105

2.湖南工程學院，湖南 湘潭 411101

1 引言

近年來，隨著移動機器人的廣泛應用，移動機器人吸引了眾多科研人員的目光。移動機器人是執行未知環境探索的主體，深受人們的關注。跟蹤控制作為移動機器人運動控制的主要部分，其目標就是要通過調節機器人的運動速度和運動方向，使機器人沿期望的無碰撞的軌跡運動。在現實中，要減少移動機器人實際軌跡與期望軌跡之間的誤差并不是一件容易的事情，移動機器人具有時變、非線性的動力學特征，由于驅動輪存在滑動和傳感器測量的誤差，再加上內部和外部的干擾和噪聲的影響，移動機器人很難實現有效、精確地跟蹤。滑模變結構控制作為一類非常特殊的非線性控制，對在預定的滑模區的運動點，與對象的參數和擾動無關，這種控制方法具有快速響應、對參數變化及擾動不靈敏、無需系統在線辨識、物理實現簡單等優點[1]，在機器人的控制領域很受歡迎。20世紀90年代，Kanayama Y、Kimura Y和Miyazaki F提出了一種基于自動移動機器人的穩定跟蹤控制方法[2]，并成功地應用于機器人Yamabico-1I，加快了滑模變結構在機器人控制領域中的應用；2004年，葉濤等人[3]設計了一種全局漸近穩定性的滑模跟蹤控制器，開創了采用反演設計思想設計滑模切函數的先河。

本文主要是在一種新的運動模型的基礎上，采用分步反演設計技術和改進的滑模變結構控制方法，對非完整約束下的移動機器人全局跟蹤問題進行了研究，證明了控制系統的穩定性，并通過與各種已經存在的控制方法相結合，提高了跟蹤的精確度，加快了算法收斂速度，實驗結果驗證了其有效性和正確性。

2 問題描述

2.1 研究對象

移動機器人要實現有效跟蹤圓軌跡，其運動必須滿足非完整約束的條件。圖1所示的移動機器人為輪式移動機器人，該機器人兩個較大的前輪為驅動輪，一個較小的后輪為從動輪。左右兩個前輪各由一個電機來驅動，如果兩個驅動輪轉速不同，從而可實現機器人的轉彎。如圖1中，假設移動機器人兩個驅動輪的軸中心點為M，點M在坐標系的位置為(x，y)及方向角為θ，v和w分別為移動機器人的線速度和角速度。設移動人左右輪軸的距離為B，則移動機器人左輪速度為vR=v+(wB/2)和右輪速度為vL=v-(wB/2)[4]。

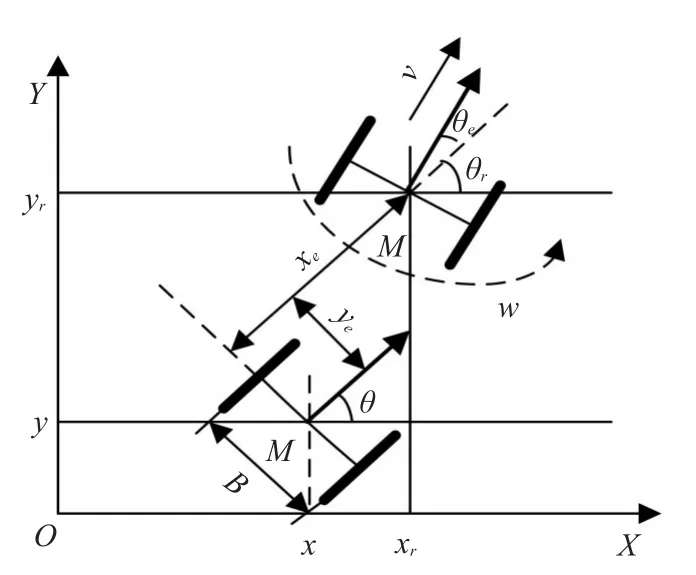
圖1 移動機器人位姿誤差表示

在移動機器人運動學模型中，考慮在實際中的應用，為了防止因輪子轉動的速度太快而產生滑動的問題，限制移動機器人的速度，要求角速度和線速度是有界的。此外，移動機器人的非完整約束條件可以用下面式子表示：

令 pT=(x y θ)，移動機器人的運動學方程為：

2.2 軌跡跟蹤問題描述

移動機器人從位姿 pT=(x y θ)移動到位姿移動機器人在新坐標系 Xe-Ye中的坐標為pe=(xeye，其中 xe表示駕駛方向誤差，ye表示橫向誤差，θe表示方向誤差。通過坐標變換，可以把移動機器人位姿誤差方程描述為：

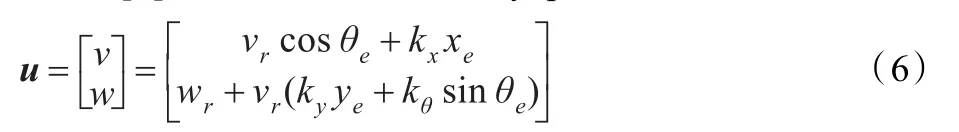
kx、ky、kθ是常量。在每一個速度中，第一項前饋部分用uf=(vfwf)T表示，第二項反饋部分用ub=(vb表示，從而可以把式（6）變換成：

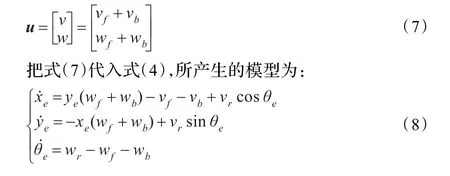
3 移動機器人跟蹤控制器的設計

對于跟蹤控制器的設計，主要是根據式（7）分成前饋和反饋兩個部分來考慮。前饋部分uf=(vf主要通過滑模變結構的方法來設計，采用改進的切換函數和趨近律，從而提高了跟蹤精確度。

3.1 前饋部分設計

引理1[3]對于任意x∈R且|x|?∞，有?(x)=xsin(arctan x)≥0，當且僅當x=0時“=”成立。

滑模變結構控制系統的設計方法一般包含兩個相互獨立的步驟：

（1）根據引理1，可設計基于反演設計的滑模切換函數如下：

通過設計滑模控制器，使s1→0，s2→0，即實現xe收斂到 ye且 θe收斂到 -arctan(vrye)，從而實現 ye→0和xe→0，進而實現θe→0。

證明 考察Lyapunov函數：

由引理1可知vryesin(arctan(vrye))≥0（當且僅當vrye=0時“=”式成立）。

又wf為移動機器人的角速度，所以wf≥0，則≤0。

（2）取指數趨近律，其表示為：

3.2 反饋部分設計

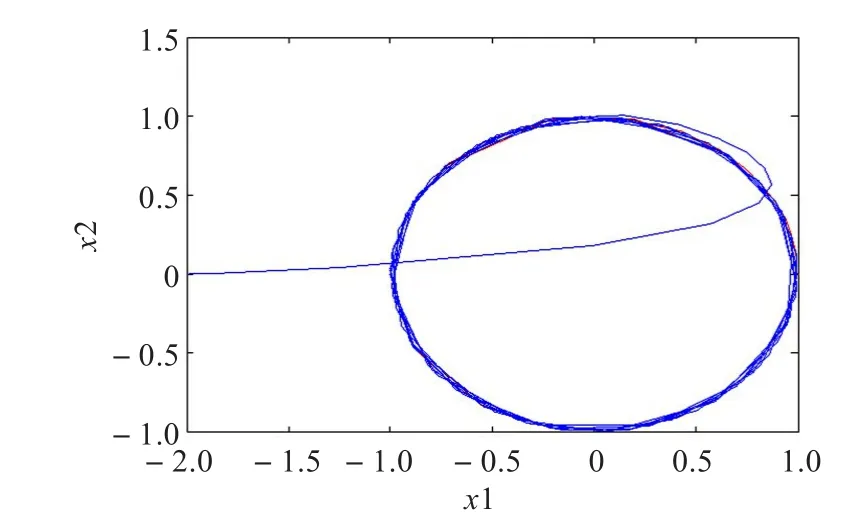
圖2 圓軌跡的位置跟蹤1

ub=(vb主要是基于Lyapunov函數來設計，在文獻[2]中，提出一種穩定性很好的控制律如式（6），這種控制方法適用于參考路徑和移動機器人實際位姿已知的情況下，可以實現高精度的位置跟蹤控制，并在機器人上成功應用。本文通過對這種控制方法的研究和分析，可以發現這種跟蹤控制方法的反饋部分為：

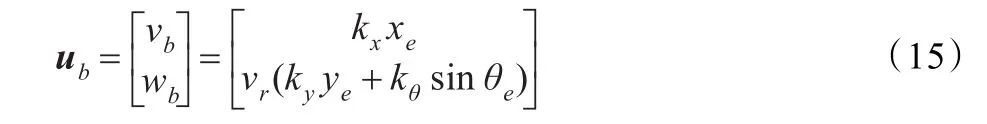
在式（15）的基礎上，Samson提出了一種新的控制律[6]：

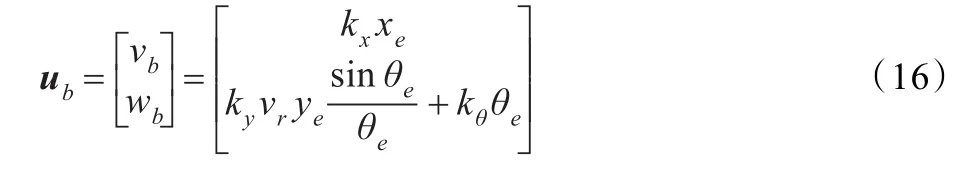
由于式（14）和式（16）就可以得到移動機器人跟蹤控制的一種含有前饋和反饋這兩個部分的新型控制器如下所示：

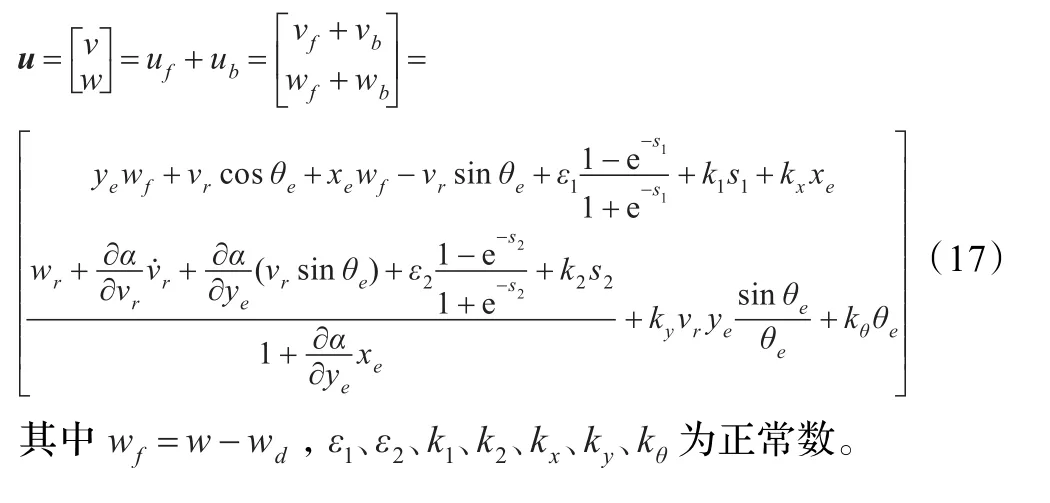
4 Simulink實驗及其分析

對以上提出的移動機器人運動控制算法，本文通過移動機器人跟蹤圓軌跡來仿真驗證。假設跟蹤線速度vr和角速度wr均為勻速運動，取wr=1.0，vr=1.0，則=0，半徑為，期望位姿為=( xryrθr)為：

取ε1=ε2=0.02，k1=k2=ky=8.0，kx=kθ=6.0，移動機器人位姿誤差初始值為[ ] 3 0 0，為了進行對照，首先只采用滑模控制律式（14），仿真結果如圖2～5所示。

采用具有前饋部分和反饋部分的控制律式（17），仿真結果如圖6～9所示。

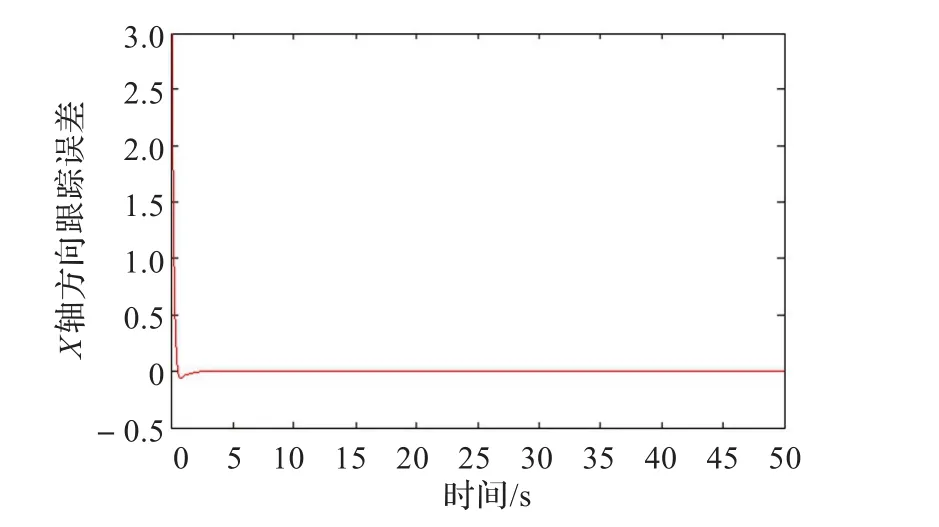
圖3 X軸方向誤差1

從仿真的結果可以看出，參數能很快收斂到最優值。這種方法與其他的方法相比，有以下優勢：（1）使用了滑模變結構的方法設計前饋部分，使控制器具有了良好的適用性和魯棒性，通過用S函數來替換符號函數，有效地提高了計算機仿真的效率，改善了滑模控制器的抖動問題。（2）通過Lyapunov設計的反饋控制器和前饋部分的結合，提高了跟蹤控制的精確度，實現了移動機器人的有效跟蹤。

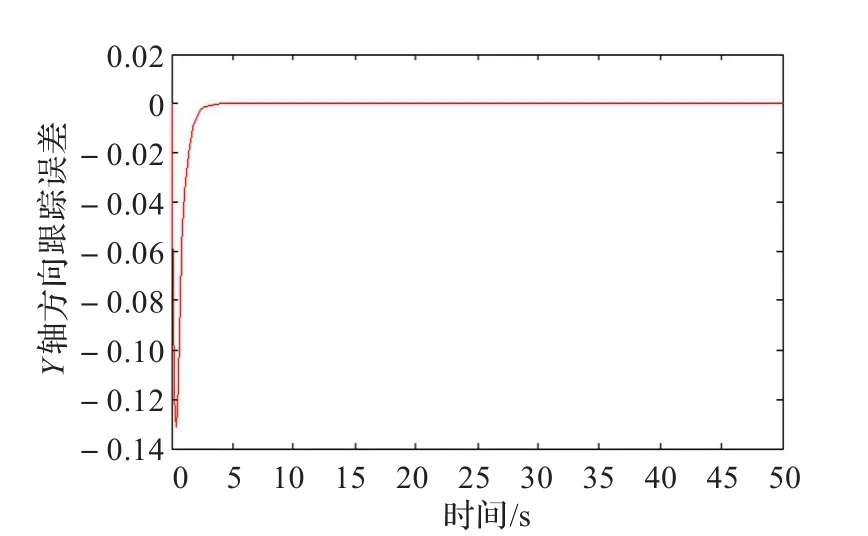
圖4 Y軸方向誤差1

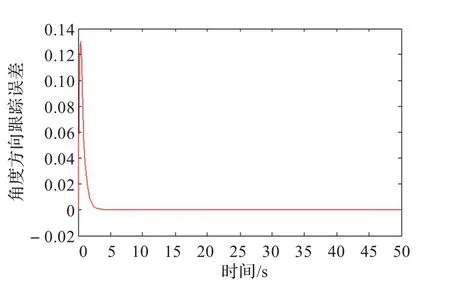
圖5 航向角度方向誤差1

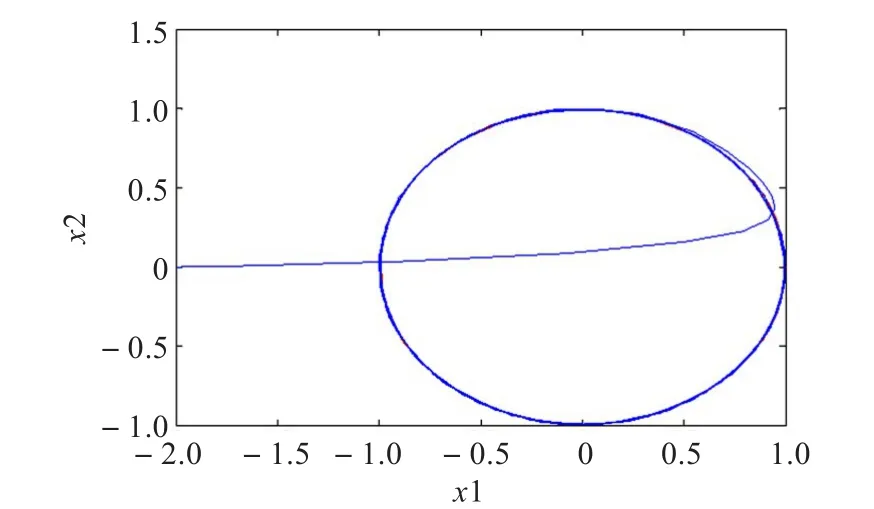
圖6 圓軌跡的位置跟蹤2

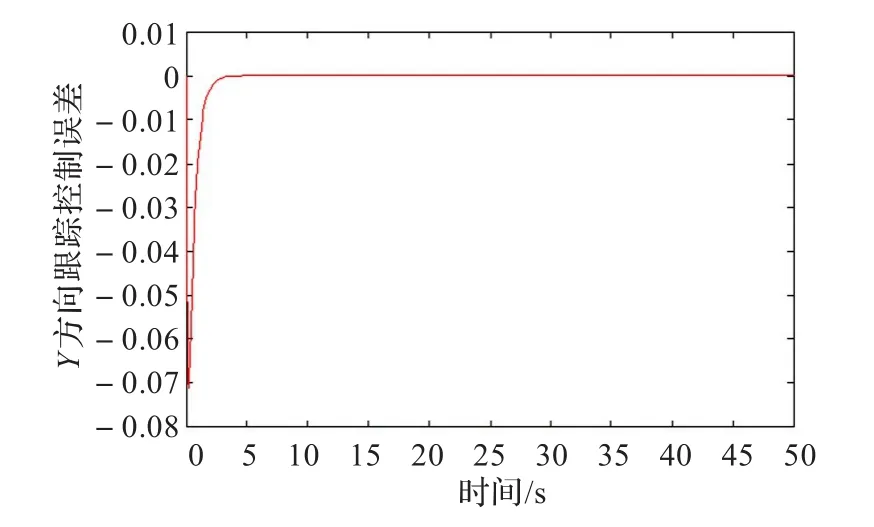
圖8 Y軸方向誤差2

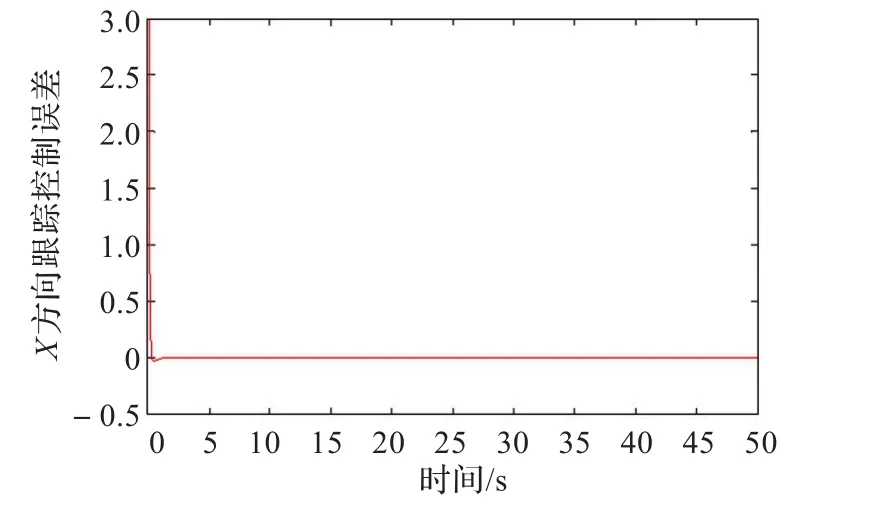
圖7 X軸方向誤差2

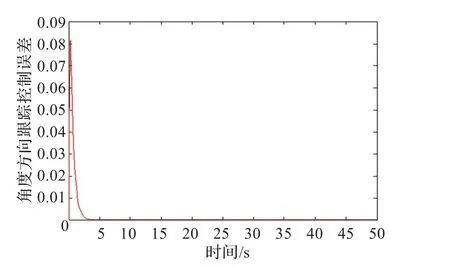
圖9 航向角度方向誤差2

5 結論

軌跡跟蹤控制是移動機器人運動控制的重要問題，本文通過在一種新的移動機器人誤差微分模型的基礎上，提出了一種具有反饋環節的滑模控制跟蹤器。這種控制算法，充分發揮了滑模變結構控制方法和反饋控制方法的優點，計算簡單，收斂速度快，具有強魯棒性和很好的穩定性，能夠有效地跟蹤參考軌跡，仿真結果驗證了這種控制理論的正確性。但是對于算法中含有的參數優化問題，還有待于進一步研究。

[1]劉金琨.滑模變結構MATLAB仿真[M].北京：清華大學出版社，2005.

[2]Kanayama Y，Kimura Y，Miyazaki F，et al.A stable tracking controlmethod foran autonomousmobilerobot[C]//Proc of IEEE International Conference on Robotics and Automation.USA：IEEE Press，1990：384-389.

[3]葉濤，侯增廣，譚民，等.移動機器人的滑模軌跡跟蹤控制[J].高技術通訊，2004（1）：71-74.

[4]Ni?ulescu M.Controlling a mobile robot along planned trajectories[J].Romania，2005，7（2）：18-24.

[5]侯銳，曹泰斌.基于LCL濾波的STATCOM改進滑模控制策略研究[J].電測與儀表，2010，47（535）：30-33.

[6]Bla?i? S.A novel trajectory-tracking control law for wheeled mobile robots[J].Robotics and Autonomous Systems，2011，59（11）：1001-1007.

[7]高為炳.變結構控制理論基礎[M].北京：中國科學技術出版社，1990.

[8]Jiang Zhong-Ping，Lefeber E，Nijmeijer H.Saturated stabilization and tracking of a nonholonomic mobile robot[J].Systems&Control Letters，2001，42：327-332.

ZHANG Yangming1,LIU Guorong1，2

1.College of Information Engineering,Xiangtan University,Xiangtan,Hunan 411105,China
2.Hunan Institute of Engineering,Xiangtan,Hunan 411101,China

This paper is mainly to study trajectory tracking control method for nonholonomic mobile robot which is based on kinematic model,with global asymptotic stability.The nonlinear control method is made up of feedforward signal and feedback signal.A feedforward part is variable structure control.Switch function of variable structure control is designed based on the backstepping method.In order to weaken chattering,the exponential rate reaching rule is used in the sliding mode variable structure control.The first method of Lyapunov is used to analyse the stability of control system,and prove that the sliding mode tracking controller is stable.A feedback part is a controller which is developed based on a Lyapunov approach.Through the interaction of the feedforward part and the feedback part,the precision for mobile robot trajectory tracking control is improved.The experimental results show that the control effect is improved obviously compared with the common method,the tracking error can be in a relatively short period of convergence.The control method has the very good anti-disturbance performances.

mobile robot;sliding mode variable structure;trajectory tracking;Lyapunov;backstepping;kinematic model

主要是對非完整約束下移動機器人的軌跡跟蹤控制進行了研究，提出了一種新型的基于移動機器人運動模型、具有全局漸近穩定性的跟蹤控制方法。這種非線性控制方法主要分為前饋和反饋兩個部分：前饋部分是一種滑模控制器，它是基于反演設計的思想設計了切換函數，采用指數趨近律，減少了滑模變結構控制的抖動，并使用Lyapunov第一法對控制系統進行了穩定性分析，證明了滑模跟蹤控制器是穩定的；反饋部分是基于Lyapunov函數的方法設計的反饋控制器。通過前饋部分和反饋部分的相互作用，提高了移動機器人軌跡跟蹤控制的精度。實驗結果表明與一般的跟蹤控制方法相比，控制效果明顯改善，跟蹤誤差能在較短時間內收斂，具有很好的抗干擾性能。

移動機器人；滑模變結構；軌跡跟蹤；Lyapunov；反演設計；運動模型

A

TP393

10.3778/j.issn.1002-8331.1202-0225

ZHANG Yangming,LIU Guorong.Novel trajectory-tracking control method for mobile robots.Computer Engineering and Applications,2013,49（23）：257-260.

國家自然科學基金（No.51177040，No.61104072）；湖南省自然科學湘潭市聯合基金重點資助項目（No.09jj8006）。

張揚名（1987—），男，通訊作者，碩士研究生，主要研究領域：移動機器人的運動控制；劉國榮（1957—），男，教授，博士生導師，主要研究領域：智能控制理論與應用、交流電機控制。E-mail：ymz716@126.com

2012-02-13

2012-03-19

1002-8331（2013）23-0257-04

CNKI出版日期：2012-06-15 http://www.cnki.net/kcms/detail/11.2127.TP.20120615.1726.037.html