自適應抗差濾波理論及應用的主要進展

楊元喜，任 夏，許 艷

（1.地理空間信息國家重點實驗室，西安 710054；2.西安測繪研究所，西安 710054；3.鄭州信息工程大學導航與空間目標學院，鄭州 450052；4.長安大學 地質與測繪工程學院，西安 710054）

1 引言

目標跟蹤或導航一般采用自適應濾波技術，因為相應的系統模型一般是未知 （或部分未知）或隨時間變化的。與 Sage－Husa自適應濾波［1-3］以及有限記憶濾波［4］不同，中國學者建立了一種新的自適應抗差濾波理論［5-6］，該理論應用抗差估計原理控制觀測異常的影響，引進自適應因子控制動力學模型誤差的影響。

自適應濾波必然涉及到誤差判別統計量以及自適應因子。于是，先后構建了4種動力學模型誤差學習統計量，即狀態不符值統計量［5-6］、預測殘差統計量［7-8］、基于觀測信息與動力學模型預測信息的方差分量比統計量［9］和基于模型預測速度與計算速度不符值統計量［10］；并建立了4種自適應因子，即三段函數模型［5］、兩段函數模型［6］、指數函數模型［11］和選權函數模型［12-13］。

若要求預測狀態向量的理論協方差矩陣等于或約等于估計的狀態協方差矩陣，或要求預測殘差理論協方差矩陣等于或約等于估計的預測殘差協方差矩陣時，又得到了兩類最優自適應因子［14］。之后又發展了分類因子自適應濾波［10］和多因子自適應濾波［15］。當多因子變成單因子時，多因子自適應濾波即為單因子自適應濾波；當多因子中僅含有位置參數因子和速度因子時，多因子自適應濾波又變成分類因子自適應濾波。

為了進一步減弱模型誤差的影響，先后又發展了基于當前加速度模型的抗差自適應Kalman濾波［16］，并研究了自適應抗差濾波與神經網絡的結合［17-18］，解決動態模型構造問題；有學者將自適應抗差濾波與誤差探測、診斷、調節 （即DIA方法，detection，identification and adaptation）相結合［19］，或與 抗 差 Kalman 濾 波［20-24］相 結 合。為 了控制非線性動力學模型誤差的影響，又提出了一種提高神經網絡泛化能力的自適應UKF濾波算法［25］和一種基于Bancroft算法的GPS動態抗差自適應濾波［26］。

2 自適應抗差濾波原理

假設線性動力學模型和觀測模型分別為

式中，Xk為tk時刻m×1維狀態參數向量，Φk，k－1為u×u維狀態轉移矩陣，Wk為動力學模型噪聲向量，Lk為nk×1維觀測向量，Ak為nk×m維設計矩陣，ek為觀測噪聲向量。假設Wk和ek的數學期望為零，且協方差矩陣分別為ΣWk和Σk，并假設Wk、Wj、ek以及ej互不相關。再進一步假設觀測殘差向量為Vk，狀態預測向量為，則觀測誤差方程及狀態預測方程為

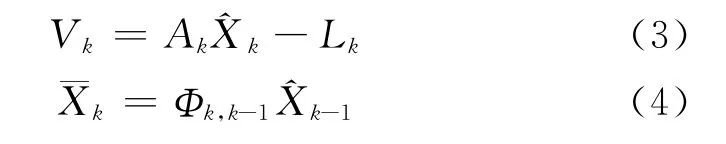
式 中，和－1分別 為tk和tk－1時 刻 的 狀 態 估 計向量。

自適應抗差濾波原則為

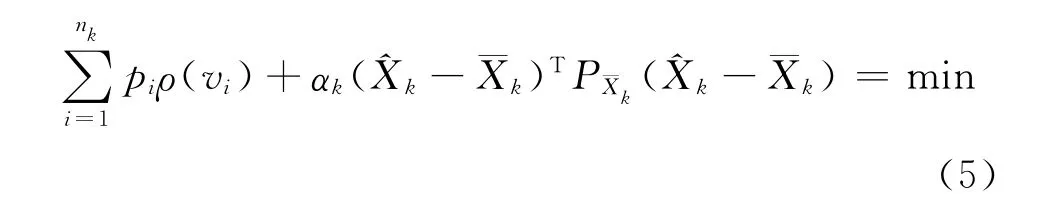
式中，ρ為連續非減凸函數［27－29］，pi為觀測向量Lk的權矩陣Pk＝的第i個對角分量，αk（0＜αk≤1）為自適應因子，＝為預測狀態向量的權矩陣。式 （5）求極值后得到［5］

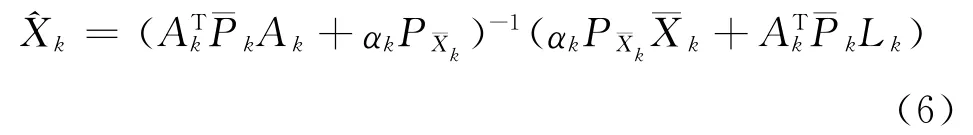
式 （6）可以等價地表示成［33，34］

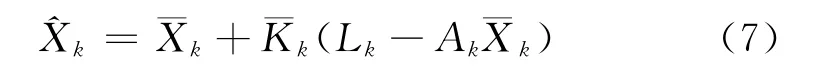
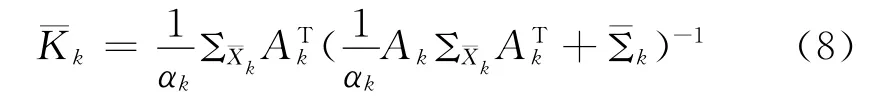
狀態向量驗后協方差矩陣為

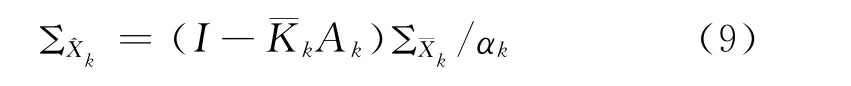
3 簡單分析

隨著自適應因子αk和觀測等價權矩陣的不同，可以得到不同的濾波解。

情形1：若αk＝0且＝Σk或＝Pk，則有

式 （10）為最小二乘平差情形，即狀態參數僅由tk歷元的觀測向量估計，不使用任何動力學模型信息。這類估計要求觀測信息豐富，且未受異常污染。

情形2：若αk＝1且＝Σk，則得到標準Kalman濾波解，即

情形3：若αk在0和1之間變化，且＝Pk，則有

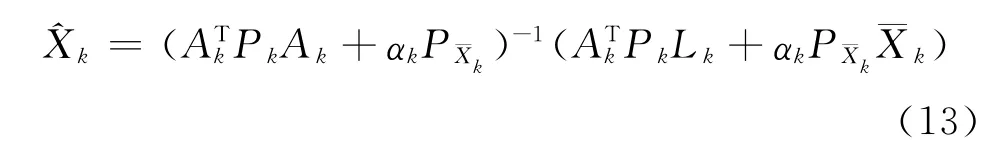
式 （13）為自適應Kalman濾波解，該估計要求觀測信息可靠。

情形4：若αk＝0，則有

式 （14）為僅利用tk歷元觀測信息的抗差估計解［28－29，31］。

情形5：若αk＝1，則有

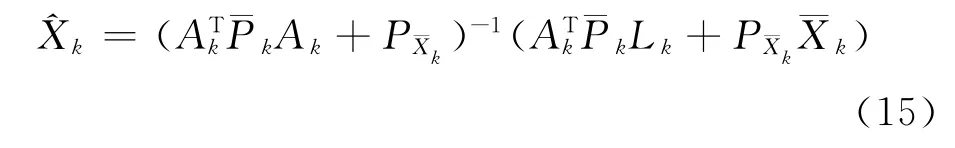
式 （15）為 M－LS濾波解［23］。

情形6：若觀測向量Lk和狀態預測向量的協方差矩陣由Sage開窗法獲得［1］，分別表示為和，即

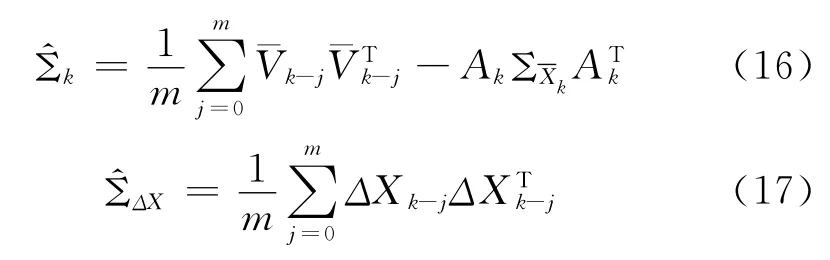
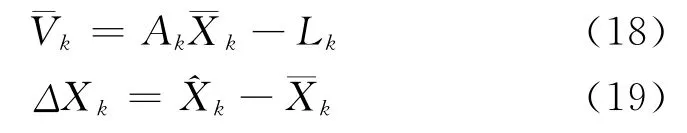
則自適應抗差濾波變成了Sage自適應濾波。

自適應抗差濾波與各種派生濾波之間的關系由圖1表示。

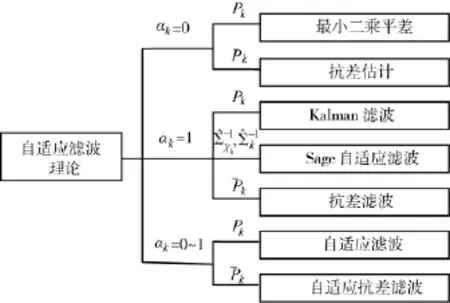
圖1 自適應抗差濾波

4 三種誤差判別統計量

4.1 狀態不符值統計量

假設在tk歷元觀測向量Lk，則由觀測信息可以獲得狀態參數的估計

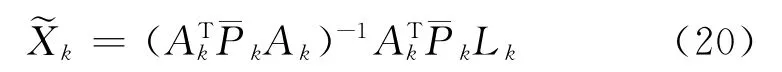
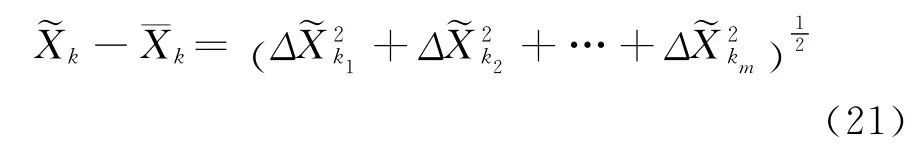
則模型誤差的判別統計量可構造成

式中，“tr”表示矩陣的跡。

簡單分析：（1）計算歷元的觀測數量要大于待估狀態參數的數量，否則不可能計算出Δ；（2）由觀測量估計的狀態參數向量應盡可能精確，否則統計量Δ不能反映動力學模型的誤差；（3）統計量Δ僅反映模型的整體誤差，任何狀態分量的擾動都將視為整體模型存在擾動。

4.2 預測殘差統計量

若觀測向量Lk可靠，預測殘差向量將反映預測狀態向量的誤差，如此，可構造如下誤差判別統計量［7-8］

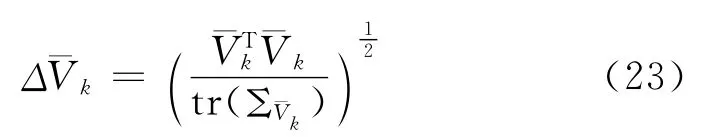
4.3 方差分量比統計量

如果將Lk和看成tk時刻的兩組觀測向量，則它們的方差分量應能反映其相應的觀測精度和模型精度，于是可用方差分量比構造誤差判別統計量，Lk和的Helmert方差分量估計公式為［35－36］

式中，和分別為Lk和的方差分量，rk和分別為Lk和的多余觀測分量，Vk和分別為Lk和的殘差向量，

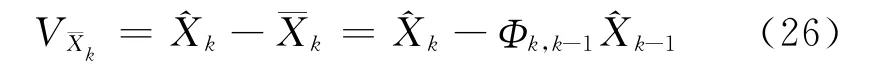
由方差分量比表示的模型誤差統計量為

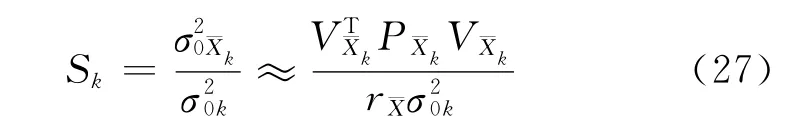
簡單分析： （1）Sk的計算需要有多余觀測分量，否則該統計量不能有效地反映模型誤差；（2）Vk和相應于相同的狀態估計向量；（3）如果采用迭代計算，則Sk的計算量稍大于Δ和Δ的計算量。

4.4 速度不符值統計量

則模型誤差判別統計量可表示成預測速度與估計速度的不符值的函數，

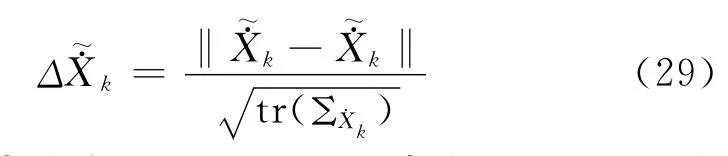
式中，為由動力學模型預測的速度向量，Σ˙Xk為相應的協方差矩陣。

簡單分析：（1）如果Δ顯著異常，則表明預測速度存在異常，或動力學模型存在較大誤差；（2）Δ的計算也要求有多余觀測信息，否則無法獲得。

5 4種自適應因子

5.1 三段函數表示的自適應因子

三段函數模型由3部分組成，即當模型誤差統計量小于一個特定閾值時，αk等于1；當模型誤差大于特定的閾值時，αk等于0；否則，αk大于0，小于1。函數形式為［5］

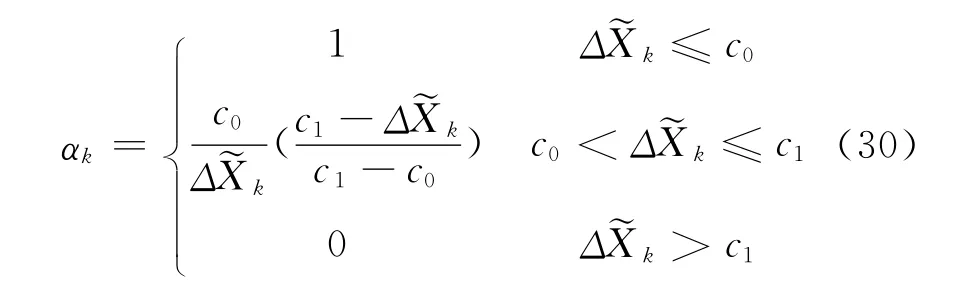
其中，c0和c1分別為兩個特定的常量，通常取值為c0＝1.0～1.5，c1＝3.0～4.5。

5.2 兩段函數表示的自適應因子

式中，c為常量，其最優值為1.0［8］。

5.3 指數函數表示的自適應因子

指數函數表示的自適應因子為［37］

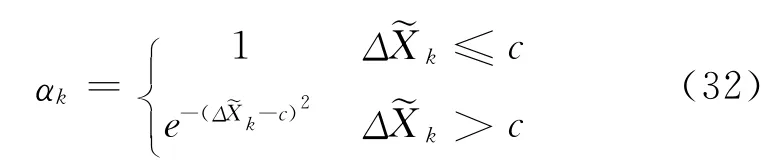
式中，c為常量，與式 （31）類似。

5.4 選權法表示的自適應因子

如果狀態參數向量服從正態分布，則自適應因子為1，否則為0［13，38］

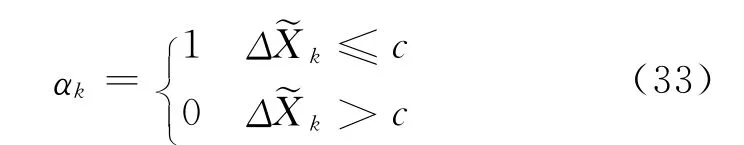
6 應用研究進展

在應用方面，自適應抗差濾波已成功應用于衛星軌道測定［39］，大地網重復觀測的數據處理［40］等；并研究了附有函數模型約束的自適應濾波導航算法［41］；在組合導航方面，發展了IMU/GPS組合導航自適應Kalman濾波算法［42］和GPS/INS組合導航兩步自適應抗差Kalman濾波算法［43］；為了同時控制有色噪聲與動力學模型誤差的影響，研究了多種有色噪聲自適應濾波算法［44］；在導航衛星鐘差擬合與預報研究中，提出了鐘差估計的開窗分類因子抗差自適應序貫平差法［45］和衛星鐘誤差實時估計的多因子抗差自適應濾波方法［46］；將自適應濾波用于物理模型與幾何觀測信息組估計地殼形變參數也取得進展［47］。

在實際工程中，自適應濾波理論和軟件已經成功應用于我國GPS道路修測工程。這里僅給出兩個典型截圖，圖2中給出了三種道路修測結果，即，差分GPS定位、接收機輸出定位和自適應抗差濾波定位。三種結果繪于同一張1/50 000的航空影像圖上 （見圖2 （a）和圖2 （b））。

圖2 自適應抗差濾波定位、接收機輸出定位及差分GPS定位的軌跡

圖2（a）和圖2（b）清楚地顯示，接收機導航結果和差分導航結果均含有明顯的系統誤差；如果差分觀測量的個數少于狀態參數的個數，則差分GPS將給不出導航結果，或給出錯誤的結果；但是自適應抗差濾波總能給出較合理的導航結果。

7 結論

業已證明，包容了觀測歷元平差、標準Kalman濾波、抗差濾波和自適應濾波的新的自適應抗差濾波不僅能控制觀測異常誤差的影響，而且具有較強的控制動力學模型誤差影響的能力。于是它是一種有效、可靠且靈活的導航定位方法。建立的四種誤差判別統計量均能可靠地判別模型誤差，四種自適應因子均能較合理地調節動力學模型信息和觀測信息對導航狀態參數的貢獻。

中國學者除不斷完善新建立的自適應抗差濾波理論體系外，還對現有自適應濾波存在的問題進行了分析［5，48］；研究了自適應抗差濾波的性質［49］；建立了分類因子自適應濾波［10］和多因子自適應濾波理論［15］；推導了最優自適應因子模型［8］。

在應用方面，自適應濾波已被成功地應用于GPS道路修測與更新工程［50］，大地網的自適應序貫平差［40］，以及衛星軌道測定研究［39］等 。

自適應抗差濾波還可應用于其他動態數據處理領域，如地殼形變分析，其中自適應因子可用來調節動力學形變模型信息的影響，抗差等價權矩陣可用來控制動態觀測 （如GPS）異常誤差對形變參數估計的影響。

［1］DENG Z.Self－tuning Filtering Theory with Applications—Modern Time Series Analysis Method［M］.Harbin：Press of Harbin Institute of Technology，2003：162－173.

［2］MOHAMED A H，SCHWARZ K P.Adaptive Kalman Filtering for INS/GPS［J］.Journal of Geodesy，1999，73（4）：193－203.

［3］WANG J，STEWART M P，TSAKIRI M.Adaptive Kalman Filtering for Integration of GPS with GLONASS and INS［C］//SCHWARZ K P.Geodesy Beyond 2000.Berlin：Springer－Verlag，2000：325－330.

［4］PANOZZO T，BORN G H，BERNELLI－ZAZZERA F.Kalman Filtering of Accelerometric Data for Aerobraking Navigation［EB/OL］.［2012－12－26］.http：//naca.central.cranfield.ac.uk/dcsss/2004/C03＿24＿PanozzoEDITfinal2.pdf.

［5］YANG Y，HE H，XU G.Adaptively Robust Filtering for Kinematic Geodetic Positioning［J］.Journal of Geodesy，2001，75（2/3）：109－116.

［6］YANG Y，XU T，HE H.On Adaptively Kinematic Filtering［C］//Selected Papers for English of Acta Geodetica et Cartographica Sinica.北京：測繪出版社，2001：25－32.

［7］徐天河，楊元喜.改進的Sage自適應濾波方法［J］.測繪科學，2000，25（3）：22－24.

［8］Yang Y，Gao W.An Optimal Adaptive Kalman Filter［J］.Journal of Geodesy，2006，80（4）：177－183.

［9］YANG Y，XU T.An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components［J］.The Journal of Navigation，2003，56（2）：231－240.

［10］CUI X，YANG Y.Adaptively Robust Filtering with Classified Adaptive Factors［J］.Progress in Natural Science，2006，16（8）：846－851.

［11］YANG Y，GAO W.Influence Comparison of Adaptive Factors on Navigation Results［J］.The Journal of Navigation，2005，58（3）：471－478.

［12］OU J，CHAI Y，YUAN Y.Adaptive Filter for Kinematic Positioning by Selection of Parameter Weights［C］//Progress in Geodesy and Geodynamics.Wuhan：Hubei Science ＆ Technology Press，2004：816－823.

［13］REN C，OU J，YUAN Y.Application of Adaptive Filtering by Selecting the Parameter Weight Factor in Precise Kinematic GPS Positioning［J］.Progress in Natural Science，2005，15（1）：41－46.

［14］YANG Y，GAO W.A New Learning Statistic for Adaptive Filter Based on Predicted Residuals［J］.Progress in Natural Science，2006，16（8）：833－837.

［15］YANG Y，CUI X.Adaptively Robust Filter with Multi Adaptive Factors［J］.Survey Review，2008，40（309）：260－270.

［16］高為廣，楊元喜，張雙成.基于當前加速度模型的抗差自適應 Kalman濾波［J］.測繪學報，2005，35（1）：15－18.

［17］高為廣，封欣，朱大為.基于神經網絡構造的GPS/INS自適應組合導航算法［J］.大地測量與地球動力學，2007，27（2）：64－67.

［18］高為廣，楊元喜，張 婷.神經網絡扶助的 GPS/INS組合導航自適應濾波算法［J］.測繪學報，2007，36（1）：26－30.

［19］TEUNISSEN P J G.Quality Control in Integrated Navigation Systems［J］.IEEE Aerospace and Electronics Systems Magazine，1990，5（7）：35－41.

［20］KOCH K R，YANG Y.Robust Kalman Filter for Rank Deficient Observation Model［J］.Journal of Geodesy，1998，72（8）：436－441.

［21］SCHAFFRIN B.Generating Robustified Kalman Filters for the Integration of GPS and INS［R］.Stuttgart：Institute of Geodesy，University of Stuttgart，1991.

［22］YANG Y.Robust Bayesian Estimation［J］.Bulletin Geodesique，1991，65（3）：145－150.

［23］楊元喜.動態系統的抗差 Kalman濾波［J］.測繪學院學報，1997，14（2）：79－84.

［24］周江文.抗差最小二乘法［M］.武漢：華中理工大學出版社，1997.

［25］高為廣，楊元喜，張 婷.一種提高神經網絡泛化能力的自適應UKF濾波算法［J］.武漢大學學報：信息科學版，2008，33（5）：500－503.

［26］張雙成，楊元喜，張 勤，等.一種基于Bancroft算法的GPS動態抗差自適應濾波［J］.武漢大學學報信息：科學版，2007，32（4）：309－311.

［27］HUBER P J.Robust Statistics［M］.New York：John Wiley，1981.

［28］YANG Y.Robust Estimation for Dependent Observations［J］.Manuscripta Geodaetica，1994（19）：10－17.

［29］YANG Y，SONG L，XU T.Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights［J］.Journal of Geodesy，2002，76（6－7）：353－358.

［30］YANG Y.Robust Estimation of Geodetic Datum Transformation［J］.Journal of Geodesy，1999，73（5）：268－274.

［31］YANG Y，SONG L，XU T.Robust Parameter Estimation for Correlated Geodetic Observations［C］//Selected Papers for English of Acta Geodetica et Cartographica Sinica.北京：測繪出版社，2002，18－24.

［32］周江文.景點誤差理論與抗差估計［J］.測繪學報，1989，18（2）：115－120.

［33］楊元喜，何海波，徐天河.論動態自適應濾波［J］.測繪學報，2001，30（4）：293－298.

［34］XU G.GPS Theory，Algorithms and Applications［M］.Berlin：Springer－Verlag，2003.

［35］KOCH K R.Einführung in die Bayes－Statistik［M］.Berlin：Springer－Verlag，2000.

［36］KOCH K R，KUSCHE J.Regularization of Geopotential Determination from Satellite Data by Variance Components［J］.Journal of Geodesy，2002，76 （5）：259－268.

［37］YANG Y，GAO W.Adaptive Integrated Navigation for Multi－sensor Adjustment Outputs［J］.The Journal of Navigation，2004，57（2）：287－295.

［38］歐吉坤，柴艷菊，袁運斌.自適應選權濾波［C］//朱耀仲，孫和平.大地測量與地球動力學進展.武漢：湖北科學技術出版社，2004：816－823.

［39］YANG Y，WEN Y.Synthetically Adaptive Robust Filtering for Satellite Orbit Determination［J］.Science in China Series D：Earth Sciences，2003，32（11）：1112－1119.

［40］隋立芬，劉雁雨，王 威.自適應序貫平差及其應用［J］.武漢大學學報：信息科學版，2007，32（1）：51－54.

［41］YANG Y，ZHANG X，XU J.Adaptively Constrained Kalman Filtering for Navigation Applications［J］.Survey Review，2011，43（322）：370－381.