空域濾波抗干擾性能的新型評定方法

李 琳，周文輝，譚述森

（1.北京衛星導航中心，北京 100094；2.北京系統工程研究所，北京 100101）

1 引言

為適應現代高技術戰爭集干擾與抗干擾、偵察與抗偵察、摧毀與抗摧毀為一體的新型作戰樣式，體現衛星導航系統功能性能的用戶設備必須具有較強的抗干擾、抗偵察和抗摧毀能力，以確保衛星導航系統效能得以充分發揮［1-7，9］。

基于陣列天線自適應處理的空域濾波作為用戶設備的主流抗干擾技術，具有對干擾類型、干擾帶寬、非理想誤差不敏感等優點［1-4，7，9］。但因基于零陷深度的性能評定方法在全面性、確切性等方面欠佳，繼而功率反演、跟蹤單星和跟蹤多星等濾波算法的定量比較，以及陣元數目、間距、布局等關鍵參量的優選尚未很好解決［9］。

本文闡述了基于干擾失效角域以及干擾失效角域因子的新型評定方法，其中干擾失效角域為（對用戶設備而言）無效干擾的來向集合，可直觀顯示空域濾波抗干擾方法的有效角度區域；干擾失效角域因子為干擾失效角域占整個空間立體角的百分比，可定量反映空域濾波抗干擾方法在整個空間的有效性。新型性能評定方法比基于零陷深度的性能評定方法全面、確切，可用于空域濾波的算法定量比較和關鍵參量優選，進而指導用戶設備的抗干擾技術方案設計與實現。

2 相關知識

2.1 衛星導航用戶設備

衛星導航系統由衛星系統、地面運行控制系統和應用系統三部分組成。應用系統中的用戶設備是體現衛星導航系統功能性能的終端設備，其工作體制有衛星無線電測定業務 （RDSS）和衛星無線電導航業務 （RNSS）兩種［7-8］。

RDSS為有源工作體制，用戶設備需響應地面測量與控制中心 （MCC）發播、衛星轉發的詢問信號，而后發送定位、報文通信和定時等服務申請信號；MCC接收服務申請信號后，根據服務申請內容作相應處理；再經由衛星轉發，使用戶設備獲得所申請的定位、報文通信和定時服務。RDSS體制以MCC的復雜性換取空間段衛星數量最少和衛星復雜度最低，僅由2顆衛星承擔導航系統的數據交換和用戶信息交換。

RNSS為無源工作體制，用戶設備需接收4顆或4顆以上衛星發播的導航信號，獲得衛星星歷、偽距觀測量、載波觀測量等，進而解算出用戶設備自身的位置、速度和時間 （PVT）［7］。

衛星的軌道高度約20 000km，有效全向輻射功率 （EIRP）僅30W左右。經過20 000km的擴散損耗后，到達用戶設備的衛星信號功率比熱噪聲還低30dB左右。用戶設備必須從如此弱的衛星信號中獲取所需信息，因而具有電磁敏感度高的特點。電磁敏感度高具有兩面性，一面是接收靈敏度高，另一面是抗電磁干擾能力弱。為此，常采用時域濾波、頻域濾波和空域濾波等抗干擾技術提高抗電磁干擾能力，以滿足復雜電磁環境下的應用需求［1-7，9］。

2.2 空域濾波抗干擾技術

與時域濾波、頻域濾波相比，基于陣列天線的空域濾波具有對干擾類型、干擾帶寬、非理想誤差不敏感等優點，成為衛星導航用戶設備的主流抗干擾技術［1-4］。

空域濾波根據衛星信號與干擾在功率、空間來向上的差異，基于陣列天線的加權矢量波束形成對干擾進行抑制。具體而言：首先利用陣列天線獲得入射平面電磁波在各陣元上的感應信號（其波程差含入射波來向信息）；然后按照合理的優化準則及約束條件獲得陣列天線加權矢量，使陣列天線方向圖形成期望接收特性，即在干擾來向形成增益很低的零陷，在有用信號來向形成增益較高的波束；而后用陣列天線加權矢量對各陣元感應信號的幅度、時延進行補償；最后將各補償信號相加，實現抑制干擾、無失真接收衛星信號的目的。

對于K個衛星信號、J個干擾的情況，陣列天線上的感應信號矢量為

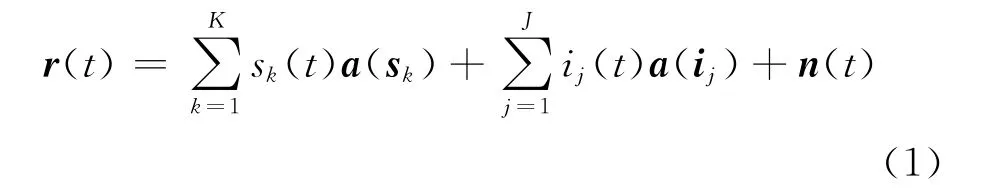
式 （1）中，r（t）＝ ［r1（t），…，rL（t）］T，a（sk）為第k個衛星信號的導向矢量，a（ij）為第j個干擾的導向矢量；n（t）＝ ［n1（t），…，nL（t）］T為熱噪聲矢量，nl（t）為第l（＝1，…，L）個陣元上的熱噪聲，包含背景噪聲和通道噪聲等；L為陣元數目。

空域濾波中常用的抗干擾算法有跟蹤單星、跟蹤多星和功率反演算法等［9］。

跟蹤單星算法是附加了對單顆衛星接收增益約束的最小輸出方差算法，即在無失真地接收指定一個衛星信號的前提下，使陣列天線的輸出方差最小。跟蹤單星算法的數學優化模型為

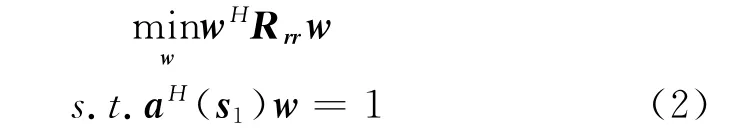
式 （2）中，w為陣列天線加權矢量，Rrr為陣列天線感應信號矢量的自相關矩陣，a（s1）為所指定衛星信號的導向矢量，記號H表示共軛轉置。

跟蹤多星算法是附加了對多顆衛星接收增益約束的最小輸出方差算法，即在無失真地接收指定Q個衛星信號的前提下，使陣列天線的輸出方差最小。跟蹤多星算法的數學優化模型為

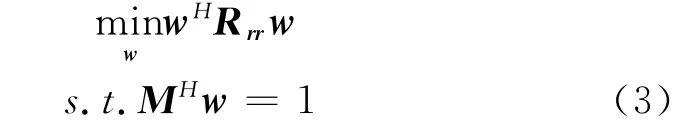
式 （3） 中，約 束 矩 陣 M ＝ ［a（s1），…，a（sQ）］，a（sq）為所指定第q（＝1，…，Q）個衛星信號的導向矢量；增益矢量1為Q維全1矢量，特別的Q取1時就為跟蹤單星算法。

跟蹤單星算法和跟蹤多星算法需已知指定衛星信號的導向矢量，進而需已知衛星位置、陣列天線位置及姿態等信息。對于無法獲得這些信息的場合，可采用功率反演算法，其數學優化模型如下

式 （4）中，約束矩陣退化為

L

維矢量δ

1

＝ ［1，0，…，0］

T

。

2.3 基于零陷深度的評定方法

空域濾波通過控制陣列天線方向圖的方向特性，區別對待干擾、衛星信號；在干擾來向上的增益很低，以抑制干擾；在衛星信號來向上的增益高，以保留衛星信號。

基于零陷深度的評定方法依據空域濾波這一特點評定其抗干擾性能［1，4，7］，具體步驟如下：

（1）取定一個干擾來向 （仰角、方位角）；

（2）根據陣列天線構型、通道特性、抗干擾算法和非理想誤差源等，計算該來向干擾時的陣列天線加權矢量；

（3）根據陣列天線加權矢量，計算陣列天線在空間各來向上的增益，獲知陣列天線方向圖特性；

（4）取陣列天線三維方向圖在干擾來向上的增益，或者 （干擾仰角上）二維剖面圖在干擾方位上的增益進行評定；

（5）若該增益比其他來向 （方位）上的增益低很多，表明空域濾波對干擾有響應。據此判定空域濾波起效；反之亦然。

顯然，該方法只能給出空域濾波對該來向干擾有無響應以及響應強弱的結論；不能給出在其他來向干擾時的響應情況，以及干擾被抑制后用戶設備的工作狀態等；用其評定空域濾波的抗干擾性能難免偏頗。

舉例說明：北斗用戶設備采用基于5元均勻圓面陣、功率反演算法的空域濾波，所接收北斗東、西衛 星 信 號 來 向 分 別 為 ［304.18°，53.32°］和［222.05°，59.82°］。這里的5元均勻圓面陣是1個陣元在圓心、其余4個陣元均勻分布于半徑為載波半波長的圓周上的陣列天線。

取定一個干擾來向 ［132.05°，39.82°］；根據陣列天線構型和2.2節的功率反演算法，計算陣列天線加權矢量；根據陣列天線加權矢量，獲知陣列天線方向圖；取圖1所示 （干擾仰角39.82°上）二維剖面圖在干擾方位角132.05°處的增益進行評定。由于圖1所示二維剖面圖在干擾方位角132.05°處的增益很低，基于零陷深度的評定方法據此判定空域濾波起效。

實際上，由圖1只能獲悉空域濾波對該來向干擾有一定程度地抑制。至于抑制程度是否滿足（用戶設備）后續信號信息處理的要求，以及在其他來向干擾情況下的抑制程度是否滿足后續要求等均不得而知。

基于零陷深度的性能評定方法在全面性、確切性方面有缺陷的原因在于：度量零陷深度不具備在全空間來向上的統計性質，也不直接反映用戶設備工作正常與否。

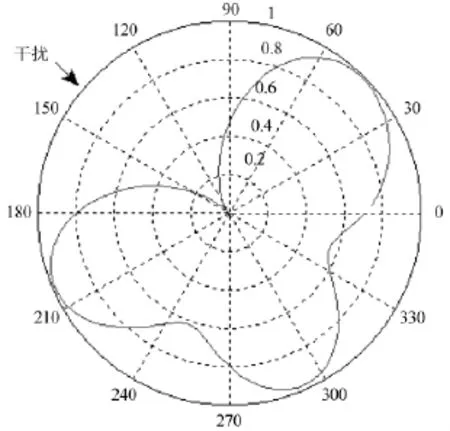
圖1 陣列天線立體方向圖在干擾仰角39.82°上的二維剖面圖

3 新型評定方法

合理的抗干擾性能度量應能反映：在空間任意來向干擾情況下，采用空域濾波的用戶設備正常工作的概率。依據這種具有全空間來向上統計性質、直接反映用戶設備工作狀態的度量，才能對空域濾波的抗干擾性能進行全面、確切地評定。

新型評定方法通過構造合理的抗干擾性能度量，繼而進行客觀、公正的性能評定。

3.1 干擾失效角域因子

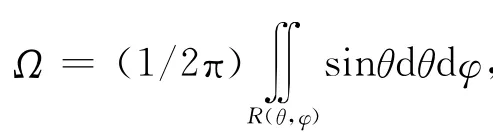
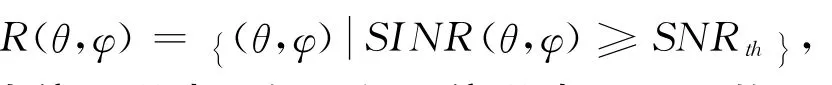
3.2 評定流程及步驟

新型評定方法的具體步驟如下：

（1）取定一個干擾來向 （仰角θ、方位角φ）；

（2）根據陣列天線構型、通道特性、抗干擾算法和非理想誤差源等，計算該來向干擾時的陣列天線加權矢量w（θ，φ）；

（3）根據加權矢量w（θ，φ），統計對視野里第k（k＝1，…，K）個衛星信號的輸出信干噪比SINRk（θ，φ）如下［9］

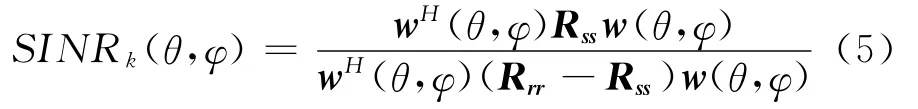
其中Rss＝Pska（sk）aH（sk）為第k個衛星信號矢量的自相關矩陣，Psk為第k個衛星信號的接收功率；

（4）重復步驟 （1）～步驟 （3），直至干擾仰角θ遍歷 ［0，90°］、方位角φ遍歷 ［0，360°）；

（5）確定正常接收視野里第k（k＝1，…，K）個衛星信號的干擾失效角域Rk（θ，φ）如下

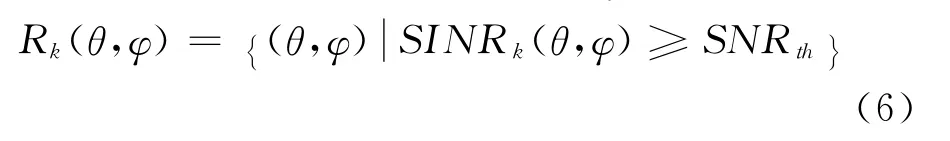
（6）確定正常接收M個衛星信號的干擾失效角域R（θ，φ）

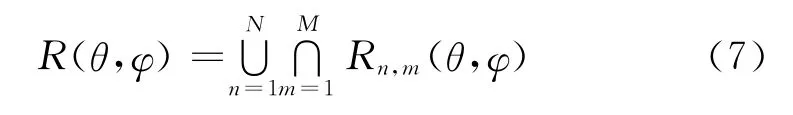
式 （7）中，Rn，m（θ，φ）為集合 ｛Rn，m（θ，φ）的第m個 元素，集合 ｛Rn，m（θ，φ是集合 ｛ ｛Rn，m（θ，φ）的第n個元素，｛｛Rn，m（θ，φ是由集合 ｛Rk（θ，φ構造出的嵌套子集合，即從｛Rk（θ，φ的K個元素中任選M個組成一個子集合，這樣的子集合共N＝個。

特別的，對于RDSS工作體制，正常接收1個衛星信號即可，則M＝1。對于視野里只有1顆RDSS載荷衛星的情況有K＝1，則N＝1，進而

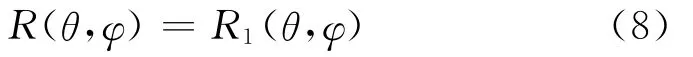
對于視野里有2顆RDSS載荷衛星的情況有K＝2，則N＝2，進而

對于RNSS工作體制，需接收至少4個衛星信號才能實現PVT解算，則M＝4，進而干擾失效角域可具體化為

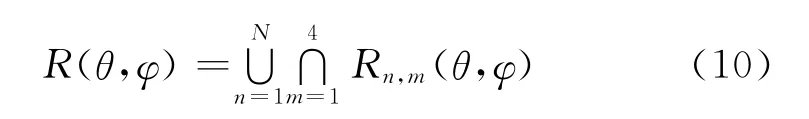
其中N＝

（7）計算干擾失效角域因子

新型評定方法的步驟 （3）～步驟 （7）與基于零陷深度的性能評定方法完全不同。

4 評定用例

下面采用新型評定方法對兩種抗干擾算法的性能進行定量比較，在兩種陣列天線布局之間進行優選。

兩種待比較算法為跟蹤單星算法和功率反演算法；兩種待優選的陣列天線布局為5元均勻圓面陣和5元均勻圓環陣 （5個陣元均勻分布于半徑為載波半波長的圓周上）。衛星信號來向與2.3節相同，門限信噪比為－20dB。

4.1 兩種算法的定量比較

下面采用新型性能評定方法，對基于5元均勻園面陣的跟蹤單星算法和功率反演算法的抗干擾性能進行定量比較。

首先，由2.2節中跟蹤單星算法、功率反演算法的數學模型，可得相應的陣列天線加權矢量分別為

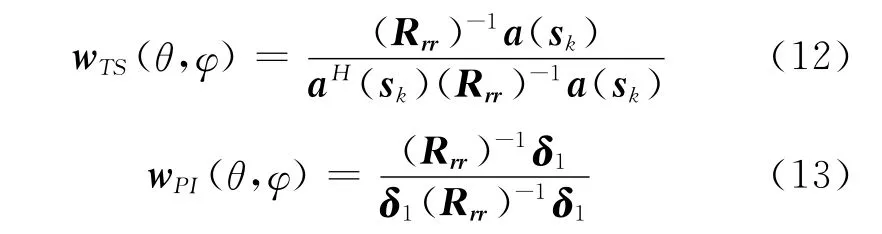
然后，可得跟蹤單星算法對視野里第k個衛星信號的輸出信干噪比為

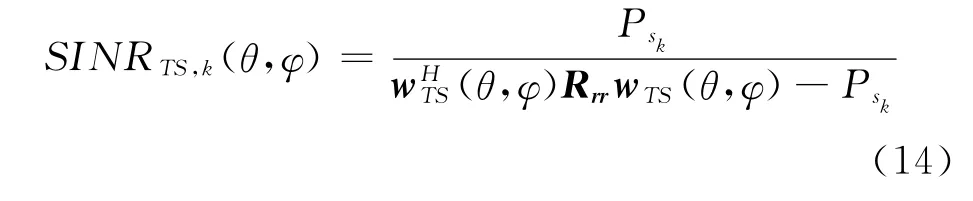
以及功率反演算法對視野里第k個衛星信號的輸出信干噪比為

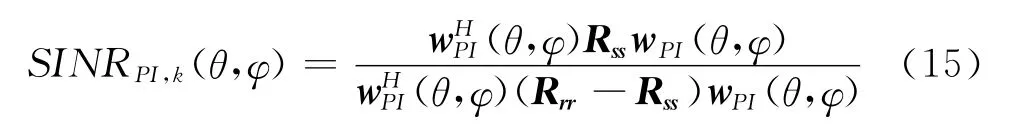
最后，與門限信噪比－20dB對比可得，圖2、圖3所示跟蹤單星算法正常接收東、西衛星信號的角域；圖4、圖5所示功率反演算法正常接收東、西衛星信號的角域。來向屬于圖2、圖4（圖3、圖5）所示區域的干擾，將不會影響用戶設備對東（西）衛星信號的接收處理；反之亦然。

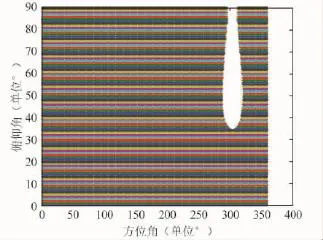
圖2 跟蹤單星算法正常接收東星信號的干擾失效角域

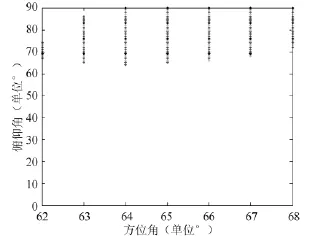
圖3 跟蹤單星算法正常接收西星信號的干擾失效角域

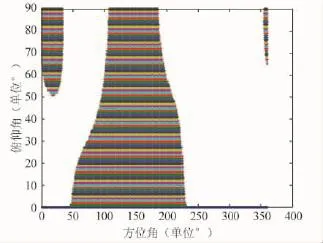
圖4 功率反演算法正常接收東星信號的干擾失效角域

因視野里有2顆衛星，根據式 （9）干擾失效角域為正常接收東、西衛星信號角域的并集，進而得到圖6所示跟蹤單星算法的干擾失效角域，圖7所示功率反演算法的干擾失效角域。

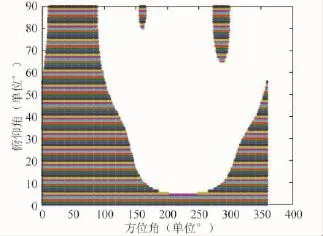
圖5 功率反演算法正常接收西星信號的干擾失效角域

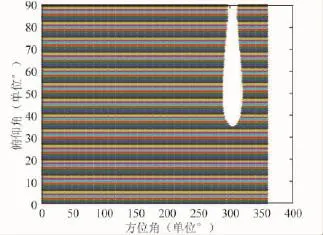
圖6 跟蹤單星算法的干擾失效角域

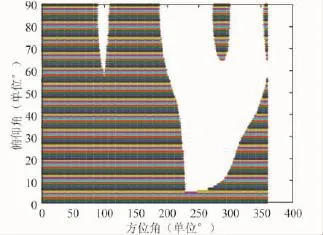
圖7 功率反演算法的干擾失效角域 （五元均勻圓面陣）

再根據式 （11）可得：跟蹤單星算法、功率反演算法對應的干擾失效角域因子分別為94.09%和59.81%，前者的抗干擾性能明顯優于后者。

新型評定方法比基于零陷深度的評定方法更全面、確切，可定量比較兩種算法的抗干擾性能。

4.2 兩種陣列布局的優選

下面采用新型性能評定方法，從基于功率反演算法的5元均勻圓面陣和5元均勻圓環陣兩種布局中加以優選。

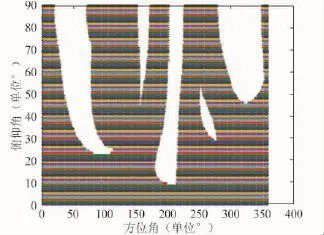
圖8 功率反演算法的干擾失效角域 （五元均勻圓環陣）

根據基于干擾失效角域因子的性能評定方法步驟，可得圖8所示基于功率反演算法、5元均勻圓環陣的干擾失效角域，以及相應的干擾失效角域因子64.65%。與4.1節中基于功率反演算法、5元均勻圓面陣的干擾失效角域因子59.81%相比，5元均勻圓環陣的陣列天線布局較有優勢。

5 結束語

新型性能評定方法所用度量干擾失效角域因子，能定量表征空間任意來向干擾情況下空域濾波方法有效的概率，比度量天線方向圖的零陷深度全面、確切。新型性能評定方法可客觀、公正地評定空域濾波方法的抗干擾性能，很好地解決了濾波算法的定量比較、關鍵參量的優選等問題。

［1］ZOLTOWSKI M D，GECAN A S.Advanced Adaptive Null Steering Concepts for GPS［C］//Military Communications Conference.California：IEEE Press，1995.1214－1218.

［2］FANTE R L，VACCARO J J.Wideband Cancellation of Interference in a GPS Receive Array［J］.IEEE Transactions on Aerospace and Electronic System，2000，36（2）：549－564.

［3］FANTE R L，VACCARO J J.Ensuring GPS Avaiability in an Interference Environment［C］//Position Location and Navigation Symposium.San Diego：IEEE Press，2000：37－40.

［4］BADKE B P.Global Positioning System Anti－jamming Techniques［D］.Arizona：Arizona State University，2002.

［5］聶俊偉，葛 銳，李垣陵，等.基于導航定位服務性能的GNSS天線陣抗干擾統計性能評估方法［J］.國防科技大學學報，2012，34（2）：81－87.

［6］KAPLAN E D，HEGARTY C J.Understanding GPS：Principles and Applications［M］.2nd Ed.Boston：Artech House，2006.

［7］李 躍，邱致和.導航與定位—信息化戰爭的北斗星［M］.2版.北京：國防工業出版社，2008.

［8］譚述森.廣義RDSS全球定位報告系統［M］.北京：國防工業出版社，2011.

［9］李 琳，周文輝，譚述森.北斗用戶機抗干擾低暴露技術研究［C］//中國衛星導航學術年會組委會.第一屆中國衛星導航學術年會文集.北京：中國全球定位系統技術應用協會，2010：78－86.