“設(shè)而不求”的教學(xué)思考

☉廣東省信宜中學(xué) 蔡玉姬

在數(shù)學(xué)解題過程中，有時需要設(shè)立一些題目中沒有直接給出的中間變量，這些中間變量可以適時消除而不用求出，對最終解決問題往往起著重要的銜接與紐帶作用，這就是“設(shè)而不求”.

在高中數(shù)學(xué)教學(xué)中，最為人熟知的“設(shè)而不求”就是涉及直線與圓錐曲線位置關(guān)系的一種解題方法：將直線方程與圓錐曲線方程聯(lián)立方程組→消元得到關(guān)于x（或y）的一元二次方程→設(shè)交點坐標(biāo)為（x1，y1）、（x2，y2）→結(jié)合判別式△>0，利用韋達(dá)定理“設(shè)而不求”→…

然而，調(diào)查發(fā)現(xiàn)，很多教師在實際教學(xué)中賦予上述方法“至高無上”的地位，并通過訓(xùn)練強化這種固定的模式程序，學(xué)生在對其“牢固掌握、熟練運用”的同時，解題能力卻沒有得到應(yīng)有的提高，反而抑制了自己思維的發(fā)展，解方程（組）等基本技能也因此而被極度弱化.

筆者認(rèn)為，任何一個解析幾何問題都是通過幾何圖形代數(shù)化、代數(shù)結(jié)果幾何化以及代數(shù)運算（簡稱“兩化一算”）而加以解決的，解方程（組）、解不等式、化簡、消元等代數(shù)變形應(yīng)該是解析幾何的基本技能.“設(shè)而不求”只是特定條件下的一種解題技巧，并不是處理解析幾何問題的通性通法.另外就“設(shè)而不求”本身而言，也不僅僅是解析幾何中利用韋達(dá)定理，“設(shè)而不求”在解決三角、代數(shù)等問題時也有著重要的作用.作為教師，對此應(yīng)有全面的理解和認(rèn)識，不能以偏賅全，更不能絕對化.

比如，“曲線的方程”與“方程的曲線”是解析幾何的核心概念，在解題中具有重要的應(yīng)用價值，但實際教學(xué)中普遍對此重視不夠.事實上，可以利用“點P（x0，y0）在曲線C：f（x，y）=0 上?f（x0，y0）=0”，將曲線上點的坐標(biāo)代入曲線方程，然后對幾個式子從整體上進(jìn)行代數(shù)變形，最終獲得想要的結(jié)果.在此過程中，曲線上點的坐標(biāo)也是“設(shè)而不求”.

例 1 已知兩條直線l1：a1x+b1y+1=0，l2：a2x+b2y+1=0 相交于點P（2，3），求過點P1（a1，b1），P2（a2，b2）的直線方程.

解：因為點P（2，3）分別在直線l1和l2上，所以

即點P1（a1，b1）、P2（a2，b2）的坐標(biāo)均滿足直線方程2x+3y+1=0，而兩點確定一條直線，故所求直線方程即為2x+3y+1=0.

點評：在解題過程中，點P1、P2的坐標(biāo)“設(shè)而不求”，首先運用 “直線上點的坐標(biāo)滿足直線方程”得到關(guān)系式①②，然后分析①②兩式在結(jié)構(gòu)上的共同特征，運用“坐標(biāo)滿足直線方程的點在該直線上”從中抽象出直線2x+3y+1=0，即為所求.這種方法需要對“曲線方程”的概念有較深刻的理解.

類似地，讀者可以嘗試解決如下問題：

我們知道，對于圓x2+y2=r2、點P（x0，y0）及直線l：x0x+y0y=r2，當(dāng)點P在圓上時，直線l表示以P為切點的圓的切線，求證：

（1）當(dāng)點P在圓外時，直線l表示從P向圓作兩條切線時，切點所在的直線.

（2）當(dāng)點P在圓內(nèi)時（不與圓心重合），過P作圓的動弦，弦的兩端點處切線的交點也為動點，直線l即為該動點的軌跡.

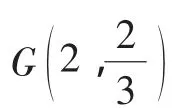
解：設(shè)B（x1，y1），C（x2，y2），則有

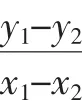
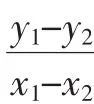
例3 設(shè)點P（3，4）為圓x2+y2=64內(nèi)一點，A、B兩點都在圓上，且∠APB=90°，以AP、BP為鄰邊作矩形APBQ，求頂點Q的軌跡方程.

解：設(shè)A（x1，y1），B（x2，y2），Q（x，y），則有

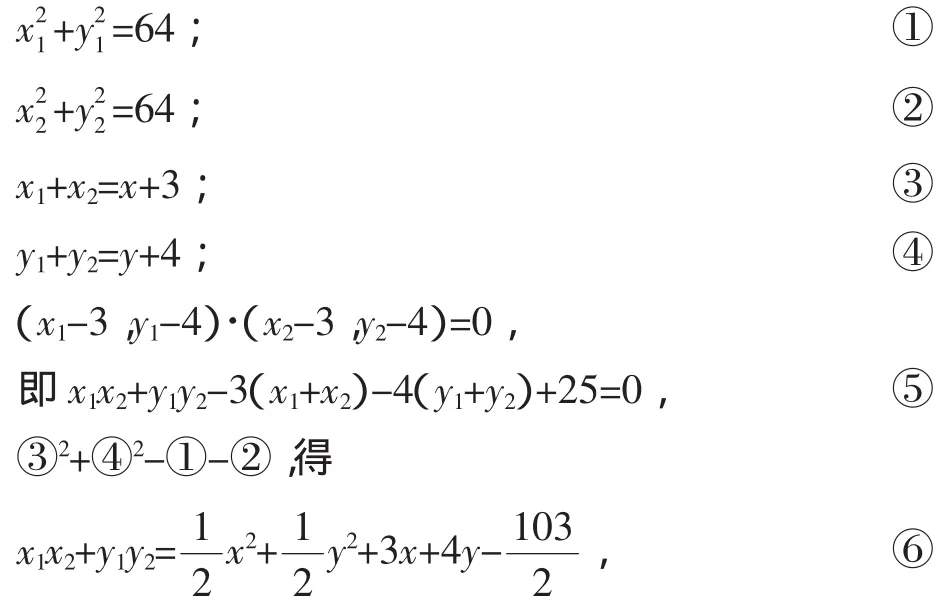
將③④⑥代入⑤，整理得x2+y2=103，即為頂點Q的軌跡方程.

點評：在解題過程中，點A、B的坐標(biāo)“設(shè)而不求”，利用“點在圓上，則點的坐標(biāo)滿足圓方程”得到①②，利用矩形的特征“對角線互相平分且鄰邊垂直”得到③④⑤.由于式子較多，變形的方向顯得尤為重要：點Q的軌跡方程應(yīng)只含有x、y，因此要消去x1、y1、x2、y2.消元時應(yīng)從式子結(jié)構(gòu)上整體把握它們之間的內(nèi)在聯(lián)系.

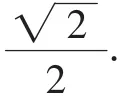
（1）求橢圓C的方程；

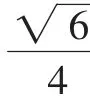
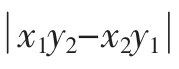
除了利用韋達(dá)定理、“曲線與方程”的概念，解析幾何中的“設(shè)而不求”還有相關(guān)點法、交軌法、參數(shù)法等，不再一一贅述.下面舉例說明“設(shè)而不求”在三角、代數(shù)中的應(yīng)用.

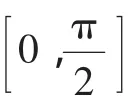
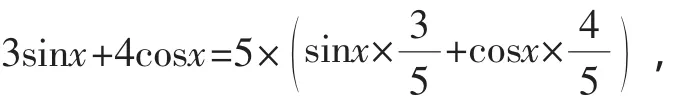
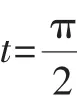
點評：很多學(xué)生會因為本題中的輔助角不是特殊角而陷入解題困境，事實上，只要對輔助角“設(shè)而不求”，緊扣其滿足的條件，換元后利用基本的三角函數(shù)y=5sint的圖像，結(jié)合三角運算（這里用到了誘導(dǎo)公式），便不難求出函數(shù)的值域.

例6 （2013年全國新課標(biāo)Ⅱ理21）已知函數(shù)f（x）=ex-ln（x+m）.

（1）設(shè)x=0 是f（x）的極值點，求m，并討論f（x）的單調(diào)性；

（2）當(dāng)m≤2 時，證明f（x）＞0.

解：（1）略；

（2）函數(shù)f（x）的定義域是（-m，+∞），當(dāng)m≤2 時，f（x）=ex-ln（x+m）≥ex-ln（x+2），故只需證明當(dāng)m=2 時，f（x）＞0.

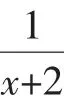
綜上，當(dāng)m≤2 時，f（x）＞0.

綜合上述分析，對于“設(shè)而不求”，我們應(yīng)形成以下兩點基本認(rèn)識：

第一，教學(xué)定位要科學(xué)，理解問題要全面.

以解析幾何為例，通過解方程（組）求出點的坐標(biāo)應(yīng)該是最基本、最重要的方法，應(yīng)居于教學(xué)的核心地位，這一點在教材的例題處理中體現(xiàn)得非常明顯.因此，教學(xué)中不能一味地灌輸“設(shè)而不求”的解題思想，反而丟失了教學(xué)中最根本的東西.現(xiàn)實中，學(xué)生想不到解方程（組）、不愿意解方程（組）、不會解方程（組）、對整體消元束手無策等情形并不少見，這與教師對“設(shè)而不求”的定位不科學(xué)有較大關(guān)系.值得注意的是，安徽省近幾年高考的解析幾何大題也在刻意地對實際教學(xué)進(jìn)行“糾偏”.

就“設(shè)而不求”本身而言，它也具有應(yīng)用的廣泛性，充滿了思辨性、靈活性和創(chuàng)造性，教師在教學(xué)中（特別是高三復(fù)習(xí)階段）應(yīng)從數(shù)學(xué)學(xué)科整體的高度引導(dǎo)學(xué)生全面地、辯證地進(jìn)行理解，而不能用固化的、單一的模式禁錮學(xué)生的思維，用機械呆板的模仿代替富有活力的思考.

第二，教學(xué)重點要突出，學(xué)習(xí)難點要突破.

“設(shè)而不求”的教學(xué)重點，首先是“設(shè)什么”、“怎么設(shè)”的問題，這是解決問題的起點；其次是列式的問題，即如何提取條件中的關(guān)鍵信息并恰當(dāng)?shù)丶右孕问交蛔詈笫谴鷶?shù)變形的問題，既涉及變形方向與目標(biāo)，又涉及變形方法與手段，往往需要從整體上進(jìn)行思考，通常也是學(xué)生學(xué)習(xí)的難點.

突出重點、突破難點的關(guān)鍵在于教師要踐行科學(xué)的教學(xué)理念.教師要真正尊重學(xué)生在課堂上的主體地位，堅決摒棄“告訴教學(xué)”，而是著眼于引導(dǎo)學(xué)生充分暴露自己的思維，進(jìn)而師生共同對學(xué)生的“相異構(gòu)想”進(jìn)行討論、辨析，對正確的想法予以肯定，對錯誤的思考予以糾正，對出現(xiàn)的障礙予以化解，通過變化問題情境實現(xiàn)正遷移，讓學(xué)生親歷獨立審題、嘗試解題、觀點碰撞、克服困難的完整過程，借此完善自己的認(rèn)知結(jié)構(gòu)，提高自己的解題能力、改善自己的思維品質(zhì).

1.于宗國.關(guān)于高中數(shù)學(xué)教學(xué)的一些思考［J］.考試（高考數(shù)學(xué)版），2011（1）.

2.劉占權(quán).提高高中數(shù)學(xué)課堂教學(xué)效率的探究［J］.新課程學(xué)習(xí)（學(xué)術(shù)教育），2011（1）.