客觀題講評應重視“對而不懂”現象

☉江蘇省揚州市江都區楊莊中學 肖世兵

數學離不開解題，數學教學離不開習題講評.習題評講課是數學教學中的重要課型，也是數學鞏固教學的重要環節.

關于試卷評講，已有不少老師做過研究：重點關注了錯題的講解與變式；主要集中于評講課課型模式、試卷評講的現狀、講評課的流程、講評要點等的研究.當然，這些是評講研究的重點，但我們也應重視對一些正確題的點評.

在實際練習中，學生的客觀題（選擇題和填空題）的答案有不少是對的，細細追問，可以發現他們獲取答案的方式是多樣的，或看出來的，或量出來的，或折出來的，或用特殊值代出來的，或用排他法篩出來的……對客觀題的評講，不少老師也只偏重于答案的獲得，大有“不管白貓黑貓，只要逮住老鼠都是好貓”之意.

值得肯定的是，在考試中使用這些技巧求解也不失為一種省時高效的方法.但一旦改變題型，將客觀題改為解答題，原有的技巧方法將隨之失效，學生的“問題”將暴露無疑，這時勢必導致部分學生紛紛“落馬”.因而，一些客觀題表面上看學生是做對了，但實質上，還有不少學生不知道、不了解或不清楚問題解答的數學原理.這就是在學生練習中，客觀存在的“對而不懂”現象.這也就需要教師重視客觀題中的“對而不懂”現象，重視對此類試題的評講.

一、“對而不懂”現象分析

1.“看出來的”答案

例1 如圖1，△ABC中，D為AB的中點，將△ABC沿DE所在直線翻折，使點A恰好落在BC上F處，若∠B=50°，則∠ADE=______.

圖1

教學片斷：

教師：此題怎么解答？

學生1（不屑的說道）：“這題太簡單了，看看答案就出來了.”（一句話逗得全班大笑）

教師：眼見不一定為實的，具體說說你怎么看到的.

學生1：顯然DE∥BC，所以∠ADE=∠B=50°.

教師：為什么DE∥BC？條件“D為AB的中點，將△ABC沿DE所在直線翻折”有什么用？

學生1（支支吾吾）：恩，還是看出來的.

教師：幾何上，我們不能將“看上去的”作為條件直接使用.對于猜想的結論，往往是需要論證的.大家一起想想，怎么解決？

（經過一段時間的思考，兩位學生給出了如下的解題思路）

學生2：連接AF，由翻折知DE⊥AF.由AD=DB=DF，可得AF⊥BC.故DE∥BC.

學生3：設AF與DE的交點為G，則由翻折可知G為AF的中點，而D又為AB的中點，故由中位線性質也可得到DE∥BC.

教師：還有其他方法嗎？抓住“中點”和“翻折的性質”，將條件產生有效關聯.

學生4：由翻折知：△ADE≌△FDE，可得DF=AD，∠ADE=∠FDE.因為D為AB的中點，所以DA=DB，所以DF=DB，所以∠B=∠DFB.又因為∠ADF=∠FDE+∠ADE=2∠ADE，∠ADF=∠B+∠DFB=2∠B，所以，∠ADF=∠B=50°.

案例分析：

此題的正確率雖然很高，但通過課堂調查，發現真正理解會做的不到25%.許多學生都是借助直觀感受看出來的，忽視對條件的充分應用，忽略了“軸對稱性質”的運用.在幾何練習中，一些學生常常將這種“看上去的”作為條件使用，把看似等邊三角形的就當等邊三角形用，看似等腰直角三角形的就當等腰直角三角形用，不是依據題意，而是憑“圖”捏造條件，按“圖”索解.初學幾何時，學生常常因畏難偷懶，不愿思考，懶于思考.如若不做講評，極易養成學生的解題僥幸心理，只注重結果而不重視過程，不求甚解，這樣不利于發展推理能力和培養嚴謹的科學探究精神.

因此，幾何習題講評時，謹防學生按“圖”索解，謹防因直觀猜想而造成的“對而不懂”.

2.“特殊來的”答案

教學片斷：

教師：解決此題時，我們應先根據題意，畫出草圖.請同學們說說你的解法.

學生1：我是這樣畫圖的：直線l取的是y=2，此時，點A（-3，2）、B（1，2），則AB=4，點P到AB的距離就是平行線間的距離，即△CBP的邊AB上的高，所以，△ABP的面積是4.

教師：將直線l特殊化為y=2，不錯的想法！還有沒有其他解法？

學生2：我是這樣畫圖的：將點P取在原點O，如圖2.設AB與y軸交于點C，則利用反比例函數的面積性質，得△CBP的面積是1，△ACP的面積是3，所以，△ABP的面積是4.

圖2

（在詢問了幾個學生都是取特殊情形解答之后，我又追問一句）

教師：除了取特殊位置解法外，在一般位置的情形下，又如何解決？

（一時間，學生陷入沉思中……）

學生3：當點P在除原點以外的其他位置時，利用“平行線間的距離”和“同底等高的三角形面積相等”，可知△ABP的面積等于△ABO的面積，再利用反比例函數的面積性質得解.

教師：很好！學生3很好地運用了轉化思想，將一般化為特殊，再轉化為基本圖形，解決此題.

解決此類面積問題，一種方法，就是化基本形；另一種方法，就是回到數學的“根”上，此題是坐標系下的三角形面積問題，確定三角形的三個頂點的坐標，即可表示三角形的面積.

教師：同學們給出了不少的解法，大家都在積極開動腦筋.仔細想想，這些解法不外乎特殊解法與一般解法兩種，特殊解法能有助于我們快速求解，但不利于我們對問題本質的把握，對問題的研究淺嘗則止，研究不深入、不徹底.一般解法更能讓我們體會到此類問題的通解通法，值得重視.

案例分析：

反比例函數背景下的面積問題是中考熱點問題，此題涉及兩個反比例函數的圖像，試題新穎，同時試題中的兩個動態條件使此類問題的解決更具有一般性和普適性.考慮試題很有研究價值，雖正確率高，教學時，還是做了評講.評講時，發現絕大多數學生在畫圖時，都選取了特殊情形（一種是將直線l的位置特殊化，另一種是將點P的位置特殊化，第三種是將直線l和點P的位置都特殊化），基本符合備課時的預見.當然，值得鼓勵的是學生能利用特殊與一般的關系進行解題也算是不錯的，但此法功利性強、應試味兒濃，不利于引導學生對數學知識的深入理解和數學本質的關注.因此，教師評講時，重點引導對一般方法的探究，突出對通解通法的掌握，同時，深刻感受一般解法與特殊解法之間的共同點和不同點.

因此，習題評講中既注重答題技巧的講解，更要關注對通解通法的講解，避免因特殊而造成的“對而不懂”.

3.“排出來的”答案

例3（2012年威海）下列選項中，陰影部分面積最小的是（ ）.

圖3

教學片斷：

學生1：采用排除法解題，選項A、B、D是課堂中研究的一些基本圖形，它們的面積都等于2，故面積最小的一定是C.

教師：通過排除法，對簡單問題作出解答，避開復雜的問題，選出正確答案，這是選擇題中常用的解題技巧之一，用于應試那絕對是省事高效的妙招.但若將選項C單獨出來，作為填空題或解答題來考查，你能避開嗎？

學生1（一邊抓耳撓腮，一邊忙于思考）：嗯……

教師：在平時練習中，我們應以弄懂問題為目標，而不應滿足于得到一個答案.事實上，這位同學雖得出正確答案，但對問題的理解還是不夠全面、到位的.一旦改變題型，即會造成不懂的現象.

（經過一段思考后，學生們陸陸續續地給出了不同的解法）

學生2：如圖4，過點M、N作MA⊥x軸，NB⊥x軸，垂足分別為A、B.

由反比例函數的k的幾何意義，可知：△MOA的面積等于△NOB的面積，從而，可得△MNO的面積等于直角梯形MABN的面積.

由點M（1，2）、N（2，1），可知MA=2，NB=1，AB=1.

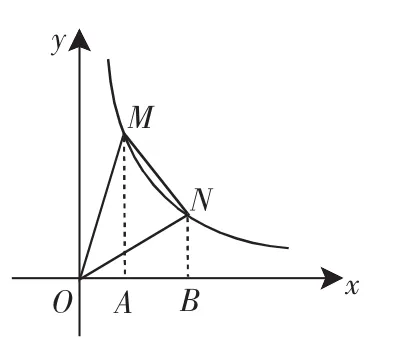
圖4

教師：該法利用反比例函數的性質，將“斜”三角形轉化為直角梯形求解，轉化得好！

學生3：如圖5，設直線MN與x、y軸分別交于點B、A.

由M（1，2）、N（2，1）求出直線MN的解析式為y=-x+3.

再求出點A（0，3）、B（3，0）.

圖5

教師：通過延長MN，舍用反比例函數，利用一次函數的知識，運用“補”的策略，進行轉化，此法跳出背景，抓住本質，不失一般.

學生4：分別過點M、N作x軸、y軸的平行線，如圖6所示.

易知點C的坐標為（2，2）.

圖6

教師：通過“補”成矩形，轉化求解.此法與上法異曲同工，但此法更為簡潔，值得推廣.

（正當筆者要講下一題時，一位男生舉手示意，說自己還有其他解法）

（鑒于課堂時間原因，筆者要求該男生說出了解題的思路，沒做具體求解）

教師：該同學利用幾何性質探究了三角形的面積，也是一種很好的思路.坐標系下的面積求解，除了用坐標知識、函數知識外，利用幾何解答，也是值得思考的角度.同學們積極思考，真的很棒，大家把熱烈的掌聲送給他們.

教師：反思總結一下，求“斜”三角形的面積的方法有哪些？其中，哪種方法最為簡潔？哪些解法更具有通用性？這些解法中體現了什么數學思想？

（出示一道變式訓練題，加強鞏固）

題目：已知在平面直角坐標系下，點A（-1，-2）、B（4，3），求△AOB的面積.

案例分析：

排除法作為解題技巧，用于應試教學無可厚非.如若改變題型，將選項C的情形，放置于填空題或解答題中，還會有如此高的正確率嗎？因此，作為平時的習題評講，應注重對數學思想方法、解題能力的訓練.筆者評講此題時，用了一節課的時間，重點探討了選項C中的“斜”三角形的面積的求法.課堂上，學生積極思考，給出了不同的解答方式，通過變式反思，學生較好地掌握了這一類型的三角形面積的基本求法，真正達到了做一題、會一類、通一片的效果，消除了此題中的對而不懂的隱患.

所以，在平時的習題評講中，對于采用排除法獲得正確答案的試題，不應忽視其的正面解決方法，謹防因用排除法而造成的“對而不懂”.

二、幾點思考

（1）因解題方法、解題技巧、學習習慣、學習心理等因素的作用，“對而不懂”現象是普遍、客觀存在的.其成因是多樣的、復雜的.既有答題技巧方面的，也有數學學習心理方面的.對于答題技巧方面，通過讓學生說解法，說思路，可以及時發現，及時彌補；對于學習心理方面，習題評講時，以激勵表揚為主，捕捉每位學生解答的閃光點，從而調動學生學習的興趣、情感等積極因素，激發勤奮好學的愿望.

（2）在平時習題評講教學中，既要關注錯題的評講，也不忽視對正題的分析研究.教師應學會講前質疑，學生真的懂了？學生可能會犯什么錯誤？學生會用哪些解法？習題是否可以變式拓展？通過教師提前預設，也能夠有效避免“對而不懂”現象.

（3）在客觀題的解答中，因題制宜，對學生技巧性的解答（如度量法、排除法、特殊法，直觀感受等）應給予充分肯定.同時，鼓勵學生嘗試從正面解答，使學生的解答更豐滿，解法更多樣，引導學生對數學本質的思考，積極培養學生“求原理、究根底”的學習作風和科學嚴謹的探究精神.

1.王道勇.淺談數學測試卷的講評［J］.中小學數學，2008（3）.

2.陶家友.精“講”巧“評”打造高效的試卷講評課［J］.中學數學（下），2013（2）.

3.陸祥雪.如何上好數學試卷講評課［J］.中小學數學，2009（7-8）.