飛機常規機動仿真的過載控制模型設計研究

李嘉林，胡孟權

（1.空軍工程大學 理學院，陜西西安 710051；2.空軍工程大學航空航天工程學院，陜西西安 710038）

0 引言

飛行仿真中通常采用飛機舵面偏角作為輸入，解算飛機的六自由度動力學模型［1］來得到飛機運動的仿真結果。在研究空戰戰法時，飛機機動動作往往先是設想所期望的機動動作，如筋斗、盤旋等，然后由仿真模型解算出運動參數的準確值。這種情況下需要采用與預期機動動作聯系更為直接的輸入參數，即采用控制飛機法向過載、航跡滾轉角和速度為輸入的動力學模型進行運動仿真。文獻［2］建立了該類仿真動力學模型，獲得了過載等輸入對應的飛機六自由度運動參數。實現預期的機動動作，實際上就是以輸入量為控制參數，以實現要求的飛機運動參數或飛行軌跡為目標的閉環控制過程，當達到飛機機動的最終狀態或滿足機動過程的要求時，即實現了預期的機動運動仿真。

本文針對涉及盤旋、躍升、俯沖、加減速、筋斗、按航路點飛行等常規機動的控制量設計問題，設計了程序以實現機動運動的仿真解算。

1 運動仿真模型

飛機機動運動仿真模型的基本原理是依據飛機運動計算模型按照一定的輸入控制量解算飛機的運動參數。運動仿真模型及其子模型的結構關系如圖1所示。圖中，動作控制模型與要計算的機動動作直接相關；運動計算模型解算飛機的運動狀態參數；動力學約束解算模型能對運動控制量進行限制或修正；當滿足動作結束條件時，動作仿真結束。

圖1 飛機運動仿真模型流程圖Fig.1 Flow chart of dynamic model of aircraft

2 過載控制律設計

文獻［2］將機動運動仿真的輸入控制量確定為（ny，γ，δt）|t或（ny，γ，Vtr）|t。其中，ny為飛機法向過載；γ為航跡滾轉角［3］；δt為油門位置；Vtr為真空速。完成預期的機動動作主要取決于對過載大小ny和過載方向的控制。對常規機動而言，可將動作分為航跡機動和經驗機動兩類。盤旋、按航路點飛行等機動的主要特點是航跡機動，要求過載的控制律滿足飛行航跡的要求。筋斗、戰斗轉彎等機動的主要特點是經驗機動，要求過載控制律符合飛行員操縱經驗。躍升和俯沖等機動的特點則兩者兼有。因此，過載控制律設計應將機動過程適當分段考慮，同時應對過載指令濾波，使之接近飛行實際。

2.1 水平盤旋和戰斗轉彎控制律

盤旋機動可分為進入、轉彎和改平三個階段。進入階段是以適當的過渡過程使滾轉角和過載達到盤旋要求的穩態值。改平階段可用一定的規律將滾轉角指令漸變到0，過載漸變到1。轉彎階段的控制律［4］如下:

式中，γc為滾轉角指令；nyc為過載指令；R為盤旋半徑；μ為航跡俯仰角；c11和c13為高度加權系數；c12為俯仰角加權系數，與速度和滾轉角有關。控制律中引入了高度和航跡角增量控制，保證盤旋機動趨近同一高度，高度浮動很小。

戰斗轉彎是以最大過載快速改變航向，達到指定航向的機動。戰斗轉彎的進入和改平段與盤旋基本類似，轉彎段直接給定要求的滾轉角指令γc，過載指令則以當地最大可使用過載為指令值。機動時高度變化量與飛機獲得的γ值有關。

2.2 筋斗機動控制律

正筋斗的滾轉角指令為零，盡量保持飛機機翼水平。過載控制分段與飛行員操縱習慣密切相關，可分為慢進入、快速拉起、保持翻轉、俯沖拉起和改平五個階段。其中，快速拉起使用筋斗的最大過載，保持接近等俯仰角速度翻轉；俯沖拉起使用適當的過載，并考慮速度與發動機狀態的合理程度，使速度接近進入速度；改平段需要精確調整過載，既能使飛機快速改平，又不至于再次跳起。主要過載控制律如表1所示。表中，θ為筋斗控制俯仰角，定義在0°≤θ＜360°區間；θ1由慢進入階段的時間t1確定。

表1 筋斗過載控制律Table 1 Load control law in loop

斜筋斗過程與正筋斗過程的進入條件相同，使用最大過載可適當減小。如斜筋斗滾轉控制進入時航跡滾轉角為10°～15°，在頂點滾轉角約為－150°。筋斗機動中根據過載ny解算控制滾轉指令，以保持筋斗在斜平面內運動。

2.3 按航路點飛行控制律

按航路點飛行定義為飛機按空間點的連線飛行，航路點的連線確定了飛機航跡的應飛航向和航跡傾斜角，因此，模型要確定到達一個航路點前的提前轉彎點。到達轉彎點的后續過程為轉彎段，當航向差較小時為調整飛行段。建立按航路點飛行控制模型的關鍵在于盡可能地貼近航路點連線飛行，并保持飛行姿態的平穩度。設計過載控制律應考慮平穩轉彎要求和航線飛行高度要求。滾轉角控制指令如表2所示。表中，Δφ為航跡方位偏差；Δγ為接近航線的控制量，正比于飛機距離連線的垂直距離，比例系數為0.0333（°）/m。

表2 按航路點飛行滾轉角控制律Table 2 Roll angle control law in route flight

過載控制指令如下:

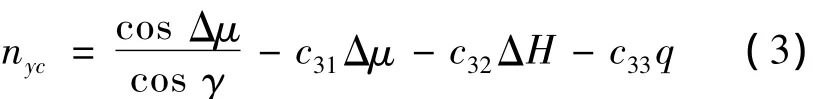
式中，Δμ為俯仰角差；ΔH為高度差；q為俯仰角速度。控制律加入了高度和俯仰角速度反饋量，使得模型較好地保持了要求的飛行高度和盡量小的俯仰姿態擺動。

2.4 躍升和俯沖機動控制律

躍升機動控制律設計要考慮拉起過程并滿足給定的躍升角，以及控制改平后高度符合要求。躍升分為快速拉起段、等角度爬升段和改出段。設計根據躍升角的大小確定最大使用過載。拉起段以2～5 s達到最大使用過載，如果未達到要求的躍升角，則采用等角速度旋轉控制飛機達到躍升角μys。等角度爬升則控制保持爬升角，速度變化由推力、重力和氣動力確定。在等角度爬升段計算改出的高度范圍，用插值法確定改出的具體時機，保證改出平飛后的高度滿足躍升高度的要求。各段控制律如表3所示。

表3 躍升過載控制律Table 3 Load control law in zoom

根據飛行員習慣，當躍升角度較大時（如大于60°）可采用半滾后拉平再翻轉的改出方式。這時需考慮滾轉角指令的兩次180°翻轉，同時在改平正飛后應考慮航向的調整，使其回到滾轉前的航向。

對于等速爬升機動過程，則要求保持進入動作初始時的速度進行爬升。過載控制分段與躍升時相同，不同的是在等角度爬升段使速度保持在要求值，同時解算推力約束條件，確保發動機能力是足夠的。

俯沖機動控制律的設計思路與躍升機動類似。

2.5 水平直線飛行控制律

水平飛行包括加減速機動動作。速度的變化主要取決于發動機推力狀態的變化。過載控制律應起到保持高度的作用，滾轉角控制律應起到修正航向的作用。考慮到該過程航向偏差較小，滾轉指令設計如表4所示。

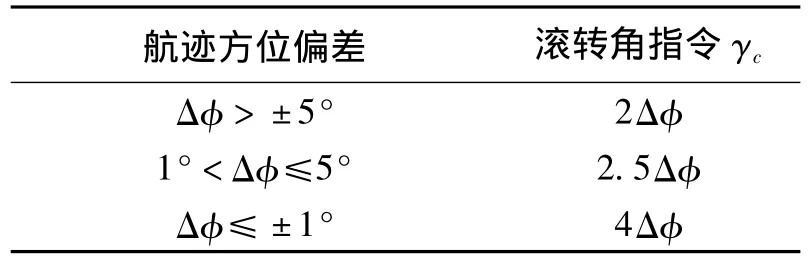
表4 直線平飛滾轉角控制律Table 4 Roll angle control law in straight level flight

過載指令為:

3 動力學約束的處理

由于先設定預期的機動動作，難免會出現設計動作不符合飛機固有的動力學特性的情況，如盤旋時速度過大而要求的盤旋半徑較小，則可能在仿真解算中遇到飛機最大使用過載限制的運動約束。在仿真解算中設置的運動約束包括平飛速度高度包線限制、發動機推力不足限制、最大使用過載限制、最小機動表速限制以及各機動仿真模型對動作設計的限制。

仿真解算過程中對運動約束問題分兩種處理辦法。一種辦法是約束導致不能繼續解算，或完成的動作不滿足設計要求時，模型停算并通知計算時遇到具體約束條件，用以調整或重新設計動作再進行解算，如推力不足以保持要求的飛行速度，或速度小于最小機動表速等。另一種辦法是在仿真解算中約束降低會降低機動能力但不影響動作完成時，模型自動以飛機最大能力完成動作，如筋斗中過載要求過大，則模型以最大可用升力系數確定機動過載。

4 仿真算例分析

以某型飛機數據為例建立運動計算模型和運動約束模型，在飛機使用范圍內以各種速度、高度初始狀態，并考慮適當的風速進行了盤旋、躍升、俯沖、加減速、筋斗、斜筋斗、按航路點飛行等機動的驗算，仿真反映出的飛行性能與飛機原始性能數據相吻合，仿真機動動作參數與預期機動設計要求相一致［5-6］。水平盤旋、水平直線加減速過程中高度變化幅度小于30 m；上升或下降過程達到高度的誤差小于5%和不大于60 m；筋斗機動符合飛行員操縱習慣，定點速度和高度與飛行員經驗描述相吻合。以躍升為例，發動機最大狀態，風速為向北2 m/s，向東3 m/s，向上2 m/s，其他條件見表5，圖2為對應的躍升仿真水平距離和高度曲線。

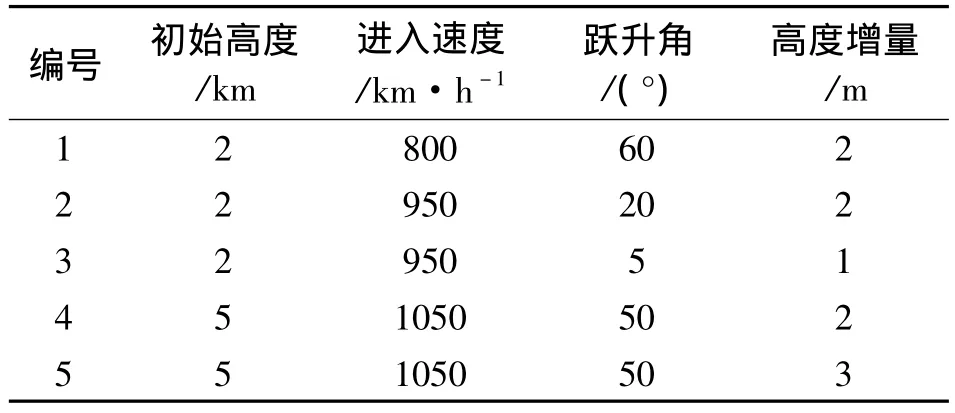
表5 躍升機動參數Table 5 Parameters of zoom

圖2 飛機躍升仿真結果Fig.2 Results of aircraft zoom simulation

設計8個航路點為算例，如圖3中按逆時針排序，虛線為航路點的連線，即實際飛行航跡的水平投影。結果表明，模型實現了繞過航路點、貼近連線的連續飛行解算，其準確度是可接受的。

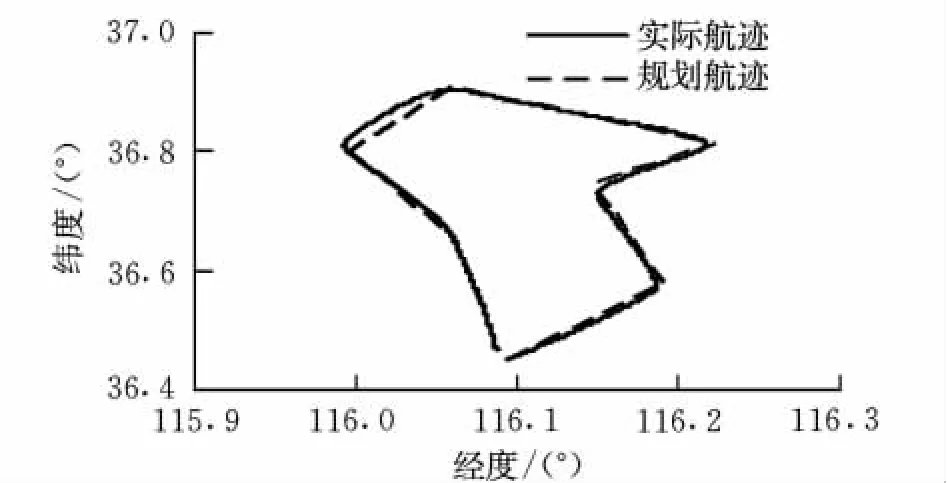
圖3 按航路點的飛行航跡Fig.3 Flight path in route flight

5 結束語

采用法向過載、航跡滾轉角和速度，或采用法向過載、航跡滾轉角和發動機推力狀態作為控制輸入，能夠較好地適用于機動動作設計。通過對控制量、控制律的設計和驗算，說明本文采用的研究方法是合理的，所設計的控制律可以滿足常規機動的仿真要求，具有一定的實用價值。

［1］陳廷楠.飛機飛行性能品質與控制［M］.北京:國防工業出版社，2007:106-121.

［2］李嘉林，胡孟權，徐浩軍，等.基于實現預期空戰機動的飛機運動模型建模［J］.空軍工程大學學報（自然版），2013，14（1）:1-4.

［3］航空氣動力手冊編寫組.航空氣動力手冊［M］.北京:國防工業出版社，1975:28-35.

［4］劉勛，高正紅，商重陽.空戰仿真中機動控制模型研究［J］.飛行力學，2007，25（1）:34-38.

［5］Hoffren J，Sailaranta T.Maneuver autopilot for realistic performance model simulations［R］.AIAA-2001-4376，2001.

［6］孔祥駿，商重陽，高正紅.殲擊機空戰機動的仿真建模研究［J］.西北工業大學學報，2007，25（3）:331-335.