可變抽樣區間泊松EWMA控制圖的經濟設計

薛 麗

（鄭州航空工業管理學院管理科學與工程學院，鄭州 450000）

0 引言

在統計控制過程中，控制圖被廣泛地用來監控過程波動，當過程出現小波動時，EWMA控制圖比傳統的休哈特控制圖有更好的監控效果[1]。為了提高控制圖的監控效率，許多學者[2-4]把固定抽樣區間的控制圖推廣到可變抽樣區間的控制圖，其中針對缺陷數服從泊松分布的情況下，叢方圓等[5]對可變抽樣區間的泊松EWMA控制圖進行了研究。盡管對可變抽樣區間控制圖的研究已經很多，對它們的經濟設計研究卻不多[6,7]。Chou&Chen[8]根據Lorenzen&Vance[9]模型研究可變抽樣區間EWMA控制圖的經濟設計，他們的研究是針對計量型特性值。但在實際生產中，許多質量特性值是計數型數據，比如生產中的產品缺陷數。在考慮了監控過程的成本費用因素之后，本文針對產品缺陷數服從泊松分布的情況，對可變抽樣區間EWMA控制圖的經濟統計進行研究。

1 可變抽樣區間的泊松EWMA控制圖

建立可變抽樣區間泊松EWMA控制圖的經濟模型之前，先介紹可變抽樣區間的泊松EWMA控制圖的構造，具體過程如下：

設X表示生產過程中的單位缺陷數,通常情況下假設X服從參數為μ的泊松分布2,...其中μ為大于0的常數。當過程處于受控狀態時,μ=μ0.當過程處于失控狀態時，μ=μ1=μ0+μ0δ，其中δ為過程均值的偏移。若取樣本容量為n，則在一個樣本中的總缺陷數就可以表示為Y=x1+x2+...+xn.它服從參數為nμ的泊松分布要對這個過程進行控制,定義泊松EWMA統計量為:

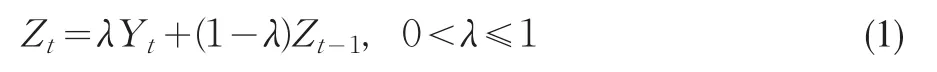
其中，λ為平滑系數,Z0=μ0.泊松EWMA控制圖的上下控制限為：

其中k1,k2分別是泊松EWMA控制圖的上下控制限系數在此需要說明：在一般的控制圖中，k1=k2.而由（1）式定義的泊松EWMA統計量Zt是一個非負數，當下控制限小于或等于零時,對過程均值的向下偏移就不會發出報警信號,即不能檢測出過程的向下偏移,所以這時取k1≠k2是很有必要的。

泊松EWMA控制圖的上下警戒限為：

其中w1,w2是分別泊松EWMA控制圖的上下警戒限系數，且0＜w1＜k1，0＜w2＜k2.選取兩個抽樣區間h1和h2，且h1＞h2＞0，若樣本點落在安全域(LWL≤Wi≤UWL),則下一個抽樣區間為h1；若樣本點落在警戒域（UWL＜Wi≤UCL或LCL≤Wi＜LWL）,則下一個抽樣區間為h2；若樣本點超出控制限（Wi＞UCL或Wi＜LCL）,則報警。

當用可變抽樣區間泊松EWMA控制圖監控過程均值變化時，需要確定八個參數VSI泊松EWMA控制圖的經濟設計就是通過使期望總費用最小確定這八個參數的最優值。

2 經濟模型建立

Lorenzen&Vance所考慮的控制圖的費用期望值包括：生產時期的質量費用；發生錯誤警報的費用；抽樣和檢查結果的費用；尋找異常原因和糾正過程的費用。根據不同的控制圖計算這幾部分的期望費用，然后除以平均循環周期，既可以得到經濟設計的費用損失函數。其中過程循環周期定義為從過程開始受控到發生異常原因過程失控，發現失控狀態和調查并消除異常原因糾正過程所經歷的時間。

在建立可變抽樣區間泊松EWMA控制圖的經濟模型之前，本文有以下幾個假設：(1)設過程開始時處于受控狀態μ=μ0;(2)失控前保持受控狀態的時間服從參數為θ的指數分布；(3)過程失控時，直到發現和糾正它以前仍然處于失控狀態；(4)在每個抽樣區間內，最多存在一個異常原因發生使過程失控。在抽樣時，異常原因不發生。根據Lorenzen&Vance的研究，把他們模型中的固定抽樣區間h修改為平均抽樣區間h0，建立可變抽樣區間泊松EWMA控制圖的經濟模型，其中目標函數為期望總費用C，公式如下：

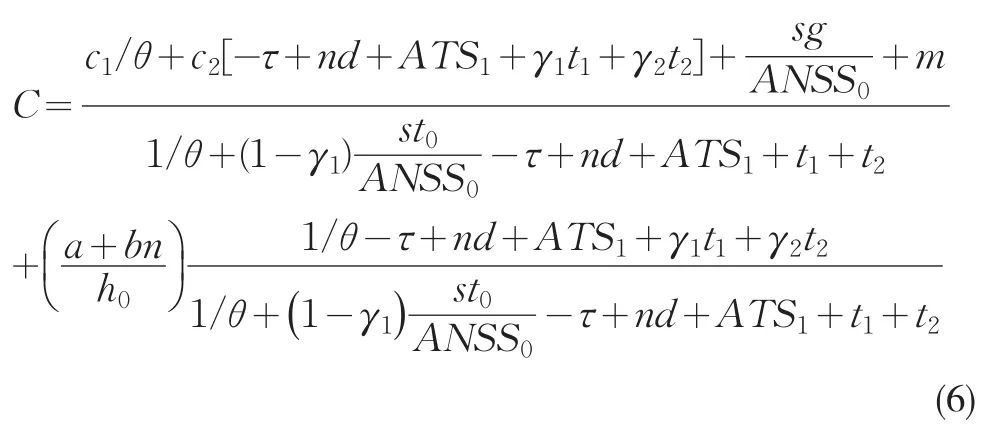
其中：a為每個樣本的固定費用；

b為單元抽樣的費用；

c1為過程受控時單位時間的質量費用；

c2為過程失控時單位時間的質量費用；

d為每次抽樣和作圖的時間；

g為錯誤警報發生的費用；

m為糾正異常原因的費用；

s為過程受控時樣本的期望值，且

τ為過程受控時在兩個樣本之間異常原因發生的時間期望值，且

t0為尋找錯誤警報的時間期望值；

t1為發現異常原因的時間期望值；

t2為糾正過程的時間期望值；

ATS1為過程失控時發出信號的平均時間；

ANSS0為過程受控時控制圖報警所需的平均樣本數；

h0為平均抽樣間隔，且h0=ATS0/ANSS0，其中ATS0為過程受控時發出信號的平均時間;

用馬爾可夫鏈法可以得出ATS0和ATS1的計算公式[5]如下：

其中，k0表示中心線處于狀態Ek0即過程在開始時處于第k0個狀態。如果控制圖的上下控制限系數k1=k2時，k0=m+1，即過程在開始時中心線處于狀態Em+1.bi(i=1,...,2m+1)為統計量Zt處于狀態Ei時所取的抽樣區間，當狀態Ei為安全域時，bi=h1；當狀態Ei為警戒域時，bi=h2.定義：

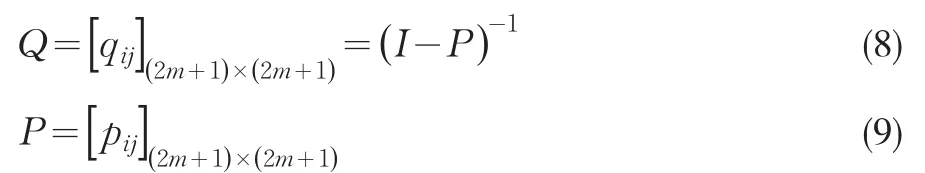
同理

其中

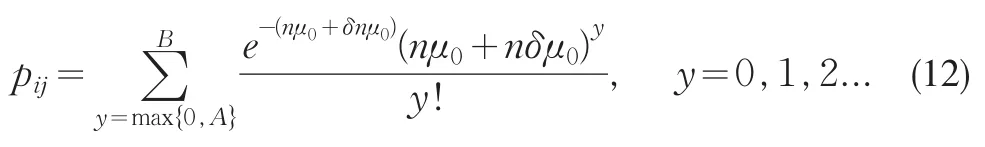
同理，用馬爾科夫鏈法可以得出ANSS0的計算公式如下：

其中，qij的公式與ATS0中的qij定義一樣，如式(8)、(9)、(10).

通過前面的討論可知期望總費用C是關于參數的函數，VSI泊松EWMA控制圖的經濟設計就是使期望總費用C最小確定這八個參數的最優值。

3 算例

z某一生產過程的質量特性值服從參數為μ的泊松分布，過程受控時μ=μ0=4，過程失控時μ=μ1=μ0+δμ0，這一生產過程可用VSI泊松EWMA控制圖來監控。本例中的費用參數和模型參數分別如下：

a=$0.5,b=$0.1,c1=$20,c2=$100,g=$50,m=$20,d=0.05hr,t0=0.5hr,t1=2hr,t2=2hr,θ=0.01,γ1=γ2=1,δ=0.5.

在matlab（version 7.0）環境下編碼遺傳算法。所求控制圖八個參數中，要求n為整數，h1,h2,k1,k2,w1,w2和λ為連續值。本例用遺傳算法求解的過程如下：

(1)開始：滿足所求參數限制條件的20個初始解被隨便選取。每個參數的取值范圍為：1≤n≤10,1≤h1≤3.5,0.01≤h2≤1,1≤k1≤4,1≤k2≤4,0.01≤w1≤3,0.01≤w2≤3,w1≤k1,w2≤k2,0.01≤λ≤1

(2)估計：計算適應性函數值來估計每個解的適應性。在本例中，適應性函數選擇為期望總費用C.

(3)選擇：在20個解中，挑選適應性好的染色體作為幸存者，組成下一代。費用高的染色體被費用低的染色體代替。

(4)交叉：隨機選取一對幸存者作為父母，來交叉產生下一代新的染色體。本例中，我們應用算術交叉法，交叉率為0.8如下：D1=0.8R+0.2M，D2=0.2R+0.8M.D1為第一個新的染色體，D2為第二個新的染色體，R、M為父母染色體。如果20對父母被隨機選擇，則應有40個孩子產生。因此，人口會增加到60個。

(5)變異：假設變異率為0.1，因為我們有60個解，則能隨機選擇6個染色體（60*0.1=6）來變異一些實驗參數。

(6)重復(2)到(6)，直到達到停止準則。本例停止準則為：運行到100代時算法停止。

在matlab環境下，運行遺傳算法程序，當運行到100代時算法停止，得到最優參數值：,n=1,h1=2.84217,h2=0.67239,k1=2.22782,k2=1.94086，w1=0.11818,w2=0.10258,λ=0.08911,C=28.6091.

4 經濟模型的最優性分析

假設某一生產過程的質量特性值服從參數為μ的泊松分布，過程受控時μ=μ0=4，過程失控時μ=μ1=μ0+δμ0，這一生產過程可用VSI泊松EWMA控制圖監控。下面對基于經濟模型設計的VSI泊松EWMA控制圖與統計方法設計的VSI泊松EWMA控制圖進行比較。兩種控制圖如下：

（1）用統計方法設計樣本容量n=3的VSI泊松EWMA控制圖。固定受控平均報警時間ATS0，使失控平均報警時間ATS1最小來確定參數的最優值。

（2）基于經濟模型設計的VSI泊松EWMA控制圖。根據經濟模型（6）確定參數的最優值。

以上兩種控制圖都在十一種模型參數的條件下，分別計算期望總費用，然后進行比較。這是一個11因素兩水平的試驗，采用正交表L16(215)進行試驗，共有16次試驗，記錄在表2。并且固定：γ1=γ2=1、t0=1，其中用統計方法設計的VSI泊松EWMA控制圖的期望總費用記為C1；根據經濟模型設計的VSI泊松EWMA控制圖的期望總費用記為C，其計算結果記錄在表3。下面固定n=3,k1=3,k2=3,w1=1.5,w2=1.5，分別計算λ=0.1，ATS0=100,150,200和λ=0.2，ATS0=300,400,500時，16次正交試驗所對應的期望總費用C1，并記錄在表3。

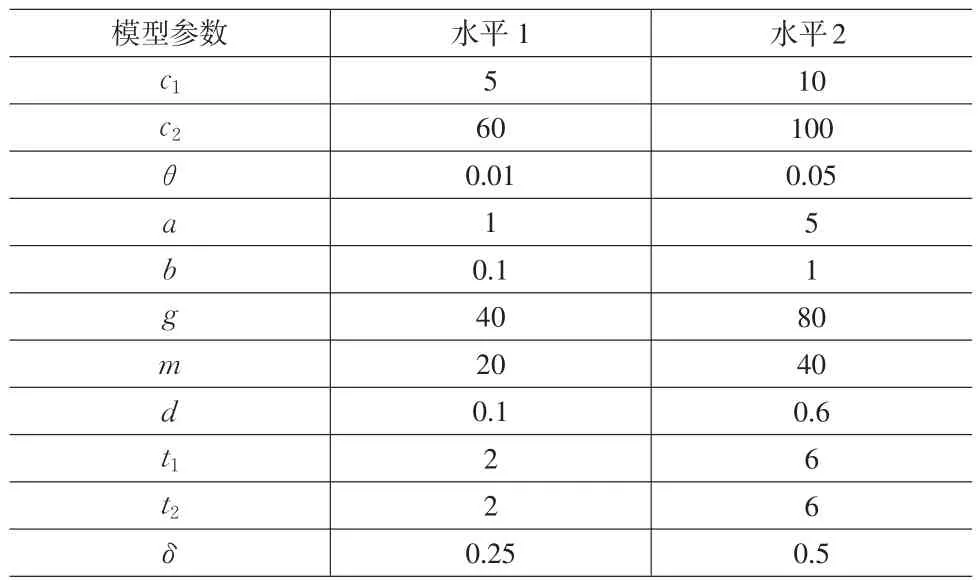
表1 11個模型參數的兩種水平

結果顯示：對于每種試驗，基于經濟模型設計的VSI泊松EWMA控制圖的期望總費用C均小于用統計方法設計樣本容量n=3的VSI泊松EWMA控制圖的期望總費用C1，所以在每種試驗下基于經濟模型設計的VSI泊松EWMA控制圖是這兩種控制圖中期望總費用最小即最優的控制圖。

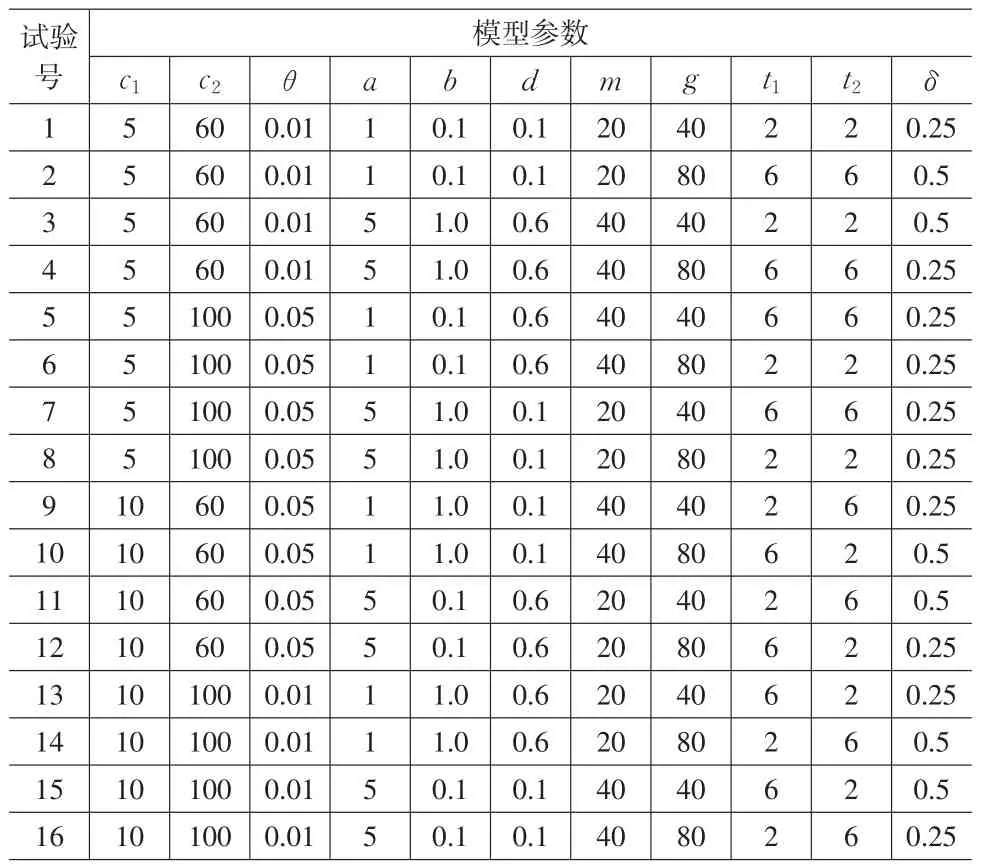
表2 根據L16(215)安排的十六次試驗

分別計算這兩種控制圖的期望總費用的平均值并記錄在倒數第二行，結果表明基于經濟模型設計的VSI泊松EWMA控制圖的期望總費用最小、最優。例如基于經濟模型設計的VSI泊松EWMA控制圖的期望總費用C的均值為32.6357，當λ=0.1，ATS0=100時用統計方法設計樣本容量n=3的VSI泊松EWMA控制圖的期望總費用C1的均值為34.4645，顯然C＜C1。

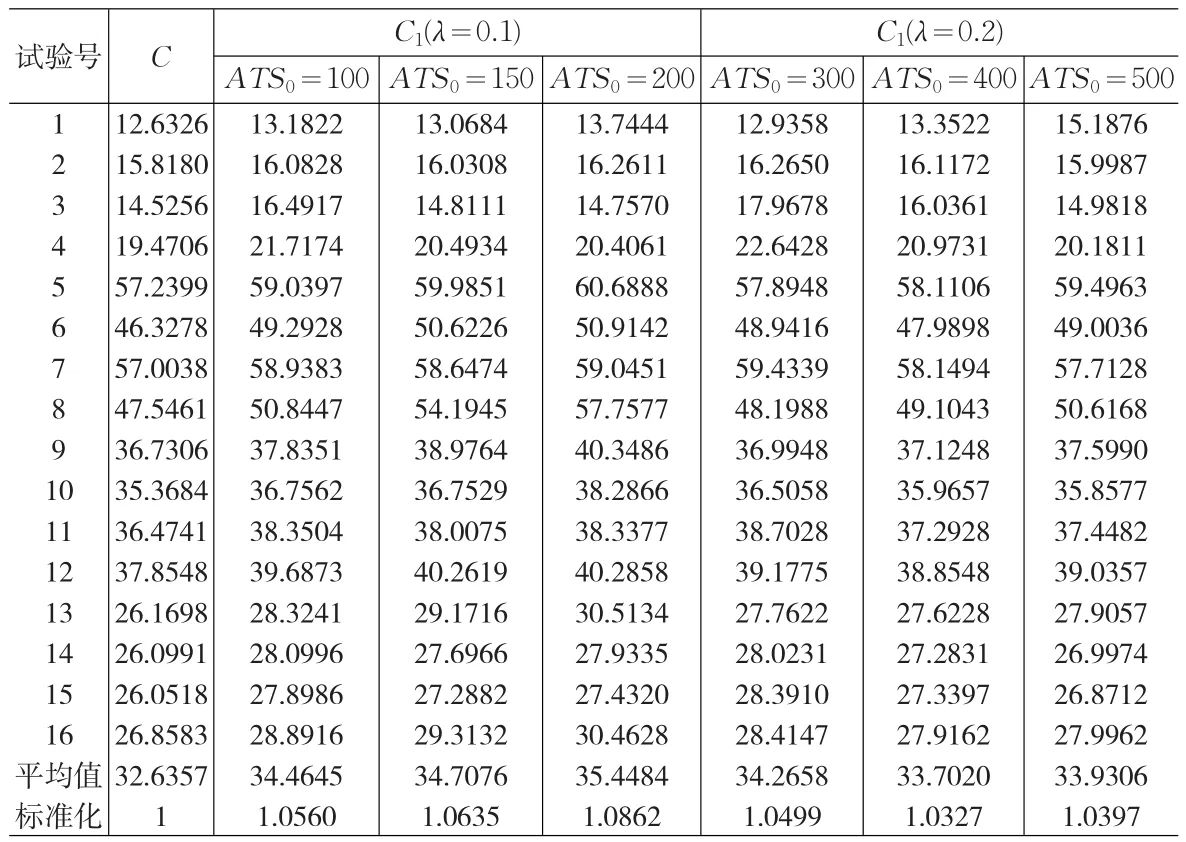
表3 最優性分析結果

最后對平均值分別標準化即除以C的均值32.6357，并記錄在最后一行。從全局的觀點得出λ=0.1，ATS0=100,150,200和λ=0.2，ATS0=300,400,500時，基于經濟模型設計的樣本容量n=3的VSI泊松EWMA控制圖的期望總費用C，分別優于統計方法設計的VSI泊松EWMA控制圖的期望總費用C1的倍數。例如：λ=0.1ATS0=150時為1.0635，說明此時的期望總費用C1為經濟模型設計的VSI泊松EWMA控制圖的期望總費用C的1.0635倍，即基于經濟模型設計的VSI泊松EWMA控制圖優于統計方法設計的VSI泊松EWMA控制圖1.0635倍。

由以上分析可以看出基于經濟模型設計的VSI泊松EWMA控制圖是這兩種控制圖中期望總費用最小即最優的控制圖。

5 結論

根據Lorenzen&Vance經濟模型，對可變抽樣區間泊松EWMA控制圖進行了經濟設計研究。使期望總費用最小，確定參數的最優值，并用遺傳算法求解模型的最優解。通過最優性分析，得出基于經濟模型設計的VSI泊松EWMA控制圖比統計方法設計的VSI泊松EWMA控制圖優越,具有較小的期望總費用。

[1]Roberts,S.W.A Comparison of Some Control Chart Procedures[J].Technometrics，1966,（8）.

[2]Reynolds,M.R.Jr,Amin,R.W.,Arnold,J.C.,Nachlas,J.A.X-bar Charts with Variable Sampling Intervals[J].Technometrics,1988,30(2).

[3]Saccucci,M.S.,Amin,R.W.,Lucas,J.M.Exponentially Weighted Moving Average Control Schemes with Vari?able Sampling Intervals[J].Communications in Statis?tics-Simulation and Computation,1992,21(3).

[4]Reynolds,M.R.Jr,Arnold,J.C.EWMA Control Charts with Variable Sample Sizes and Variable Sampling In?tervals[J].IIE Trans actions,2001,32(6).

[5]叢方圓,趙選民，師義民，王彩玲可變抽樣區間的Pois?son EWMA控制圖[J].數學的實踐與認識,2007,37(13).

[6]Chou,C.Y.,Cheng,J.C.,Lai,W.T.Economic Design of Variable Sampling Intervals EWMA Charts with Sam?pling at Fixed Times Using Genetic Algorithms[J].Expert Systems with Applications,2008,（34）.

[7]Serel,D.A.,Moskowitz,H.Joint Economic Design of EW?MA Control Charts for Mean and Variance[J].European Journal of Operational Research,2008,(184).

[8]Chou,C.Y.,Chen,C.H.,Chen,C.H.Economic Design of EWMA Charts with Variable Sampling Intervals[J].Quality&Quantity,2006,(40).

[9]Lorenzen,T.J.,Vance,L.C.The Economic Design of Control Charts:a Unified Approach[J].Technometrics,1986,(28).