縱向數(shù)據(jù)非參數(shù)模型的修正二次推斷函數(shù)估計

趙明濤，何曉群

（1.中國人民大學統(tǒng)計學院，北京 100872；2.哈爾濱理工大學應(yīng)用科學學院，哈爾濱 150001）

0 引言

縱向數(shù)據(jù)[1,2,3]涉及到對不同個體的重復觀測數(shù)據(jù)，其獨特的結(jié)構(gòu)使得個體內(nèi)的觀測趨于相關(guān)，如何處理這種個體內(nèi)的相關(guān)性是研究縱向數(shù)據(jù)不可回避的問題，這不僅是縱向分析的難點，也正是諸多縱向研究的出發(fā)點。邊際建模[1,2,3]方法是一種典型的縱向分析方法，其研究的重點為響應(yīng)變量與協(xié)變量的總體效應(yīng)，而把個體內(nèi)的相關(guān)性視為討厭參數(shù)。邊際模型的優(yōu)點在于分別對均值和方差進行建模，只要均值模型假設(shè)正確，無論方差模型假定是否正確，總能得到均值部分的相合估計[1,2,3]。作為擬似然[4,5]方法在縱向研究中的一種推廣，廣義估計方程（GEE）方法由其諸多優(yōu)點已廣為大家熟知。然而，GEE估計在其估計效率以及解釋性等其他方面也存在一些缺點[6]。

針對GEE存在的這些問題，二次推斷函數(shù)[7]（QIF）則彌補了GEE的諸多不足。QIF通過對工作相關(guān)矩陣的逆矩陣進行基矩陣展開近似，則避免了對討厭參數(shù)的估計；然后構(gòu)造擴展得分函數(shù)，進而利用廣義矩方法（GMM）構(gòu)造估計的目標函數(shù)，則不僅提高了估計的效率，得到了比GEE估計更加穩(wěn)健的結(jié)果，而且使得估計結(jié)果總會存在且具有良好的大樣本性質(zhì)（相合性、漸近正態(tài)性）。同時，由于QIF本身是一個形式明確的推斷函數(shù)，故而可以直接運用于關(guān)于模型的假設(shè)檢驗[7]。

在數(shù)值實現(xiàn)方面，修正二次推斷函數(shù)[8]（MQIF）則克服了在一些情況下QIF中最優(yōu)權(quán)矩陣矩陣奇異的情形。MQIF通過一個線性收縮估計量替代最優(yōu)權(quán)矩陣，使得在任何情況下最優(yōu)權(quán)矩陣都是可逆的，而且提高了估計的精度。常用的Newton-Raphson數(shù)值迭代算法，由于需要求解雅可比矩陣的逆矩陣，不僅計算量太大，更有可能會出現(xiàn)雅可比矩陣奇異的情況，使得迭代不收斂或者得到的估計偏差太大。割線法基于向量分割方法，不需要計算雅可比矩陣的逆矩陣，不僅大大減少了計算量，而且避免了雅可比矩陣奇異的情形。對于縱向數(shù)據(jù)的非參數(shù)模型，本文選用回歸樣條[9]的方法，通過一組基對其展開近似，進而構(gòu)造基函數(shù)系數(shù)的MQIF。在數(shù)值實現(xiàn)方面本文則選用割線法迭代求解。

1 估計過程

假設(shè)縱向數(shù)據(jù)集合

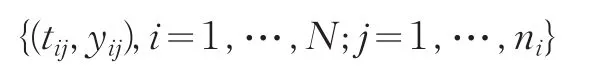
滿足模型yij=f(tij)+εij，其中tij與yij分別為第i個個體的第j次觀測時刻點以及相應(yīng)的響應(yīng)變量，εij為零均值隨機誤差。f(?)為未知平滑函數(shù)。下面給出模型的低階矩的假設(shè)條件[4,5,6]：

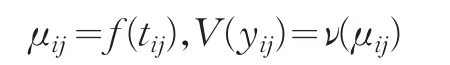
其中ν(?)是已知的方差函數(shù)，進一步假設(shè)不同個體的觀測之間相互獨立。

采用基函數(shù)展開的方法近似未知平滑函數(shù)f(t)，此處不僅僅限于某一種基。不失一般性，選擇的一組基向量為：B(t)=[B1(t),…,Bk(t)]T，則可以得到f(t)=B(t)Tγ，其中γ為對應(yīng)的k×1維基函數(shù)系數(shù)向量。由此得到新的均值條件為

假設(shè)第i個個體內(nèi)觀測的協(xié)方差陣為，其中R(α)為工作相關(guān)矩陣，Ai為第i個個體觀測的邊際協(xié)方差陣，顯然Ai為一對角陣，進而可以得到關(guān)于γ的GEE如下：

假設(shè)工作相關(guān)矩陣的逆矩陣R-1(α)有基矩陣展開形式，將其代入（1），并構(gòu)造擴展得分向量其中

為了避免出現(xiàn)C奇異的情況，根據(jù)GMM的思想，我們利用最優(yōu)權(quán)矩陣的一個可逆的線性收縮估計來替代C，進而構(gòu)造關(guān)于基函數(shù)系數(shù)的γ的修正二次推斷函數(shù)（MQIF）。不妨假設(shè)

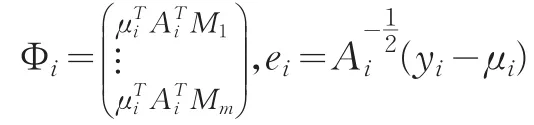
則得到：

且ei與ej相互獨立。不妨假設(shè)Ri=var(ei)，則對于任何固定設(shè)計，最優(yōu)權(quán)矩陣為，由此得到[14,15]E(C)=WN且

定義內(nèi)積＜H,K＞=其 中H∈?p×m，K∈?p×m，則矩陣范數(shù)為則得到WN的一個線性收縮估計為其中為單位陣。顯然，一定條件下，在二次期望損失意義下SN為WN的漸近最優(yōu)的相合估計。由于SN中的系數(shù)是未知的，故給出SN的估計量為其中

對于固定設(shè)計，在滿足一定條件下，有

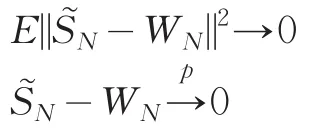
由此構(gòu)造基函數(shù)系數(shù)γ的修正二次推斷函數(shù)為

得到γ的修正二次推斷函數(shù)估計為

顯然所構(gòu)造的修正二次推斷函數(shù)QN(γ)則避免了二次推斷函數(shù)中容易出現(xiàn)的權(quán)矩陣奇異的情形，使得權(quán)矩陣總是可逆的。

實際中通常利用Newton-Raphson迭代求解，然而在復雜數(shù)據(jù)情形下，由于需要計算雅可比矩陣的逆，使得迭代算法的計算量很大難于實現(xiàn)。不僅如此，在某些特定情況下也可能會出現(xiàn)雅可比矩陣奇異的情形，使得Newton-Raphson算法無法實現(xiàn)。為了避免這些問題，我們利用割線法迭代求出γ的數(shù)值估計。割線法的迭代公式[16]為

第一步：給出γ的初始值以及收斂閥值ε0；

否則返回第二步迭代計算，直到收斂為止；

2 估計的漸近性質(zhì)

本節(jié)我們將研究上述估計過程的大樣本性質(zhì)，再給出大樣本性質(zhì)前，我們先給出一些必要的假設(shè)條件[13,14]。

條件1：最優(yōu)權(quán)矩陣WN→W0,a.s.，其中W0為一個可逆的常矩陣；

條件2：基函數(shù)系數(shù)γ是可識別的，也即存在唯一的γ0∈S，滿足均值模型假設(shè)E(gi(γ0))=0，其中S為基函數(shù)系數(shù)空間；

條件3：基函數(shù)系數(shù)空間S為一個緊空間，并且γ0為S的一個內(nèi)點；

條件4：E(gi(γ))關(guān)于γ連續(xù)；

條件5：(γ)關(guān)于γ的導數(shù)存在連續(xù)，且

下面給出基函數(shù)系數(shù)估計?的漸近性質(zhì)：

定理1：若條件（1～4）滿足，則通過（4）得到的γ?存在且

證明：顯然修正二次推斷函數(shù)有界，因此基函數(shù)系數(shù)γ的估計存在。不妨設(shè)U為γ0的任意一個鄰域。需證?不可能落在U的外邊。

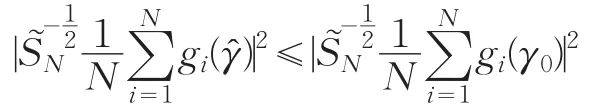
由大數(shù)定律和條件（1）可知：

對任意一個緊集，有如下一致大數(shù)定律：

由此可以得到

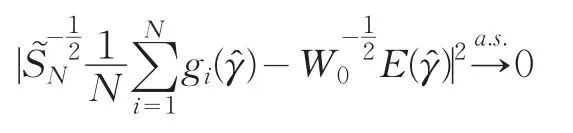
定理2：若條件（1～5）均滿足，則通過（4）得到的基函數(shù)系數(shù)估計是漸近正態(tài)的

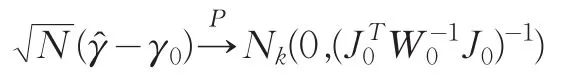
證明：由于?是由（4）得到的，所以可得到根據(jù)泰勒展開得到：

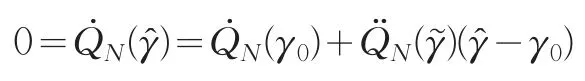
其中γ?位于γ?和γ0之間。因此有

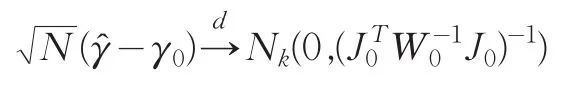
下面給出定理2的兩個推論：

推論1：基函數(shù)系數(shù)γ的修正二次推斷函數(shù)估計γ?的協(xié)方差矩陣的相合估計為

推論2：假設(shè)γ?的均值和協(xié)方差都存在，在定理2的條件都滿足的情況的估計為其協(xié)方差矩陣的估計為且f(t) 的100(1-α)%的置信區(qū)間為：

3 數(shù)值模擬

考慮模型[13]其中i=1,…,200。每個個體被觀測的時刻點集為{0,1,…,30}，每個真實的觀測時刻點與規(guī)定的時刻點之間的誤差服從均勻分布U(-0.5,0.5)，并且除了起始時刻點外，其他時刻點的觀測缺失的概率為0.6。假設(shè)個體內(nèi)的相關(guān)結(jié)構(gòu)為可交換結(jié)構(gòu)且ρ=0.8，εij～N(0,2)。對待上述兩個模型分別選用基B(t)=[1,t,t2,t3]T與B(t)=[1,t]T，利用（4）求解基函數(shù)系數(shù)γ的MQIF估計γ?，重復多遍，求均值，進而得到擬合值。

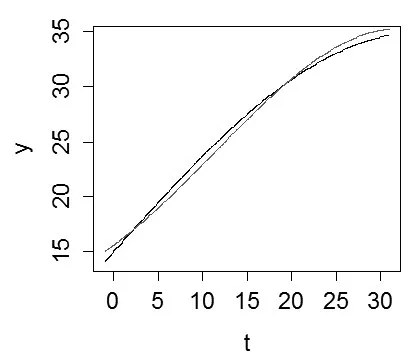
圖1

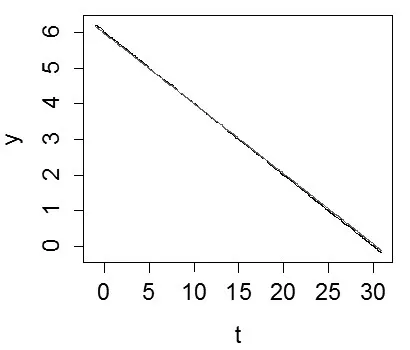
圖2

圖1與圖2分別給出了真實的平滑函數(shù)y=15+20sin的曲線及其擬合曲線，其中黑色實線為真實曲線，紅色實線為擬合曲線。從圖上看出，在觀測時段內(nèi)，兩個真實的平滑函數(shù)與其MQIF估計的擬合曲線幾乎重合，擬合效果很好。由此說明了文中所提方法的有效性以及實用性。

[1]王啟華，史寧中，耿直.現(xiàn)代統(tǒng)計研究基礎(chǔ)[M].北京：科學出版社,2010.

[2]Diggle P J,Liang,K Y ，Zeger.Analysis of Longitudinal Data[M].Lon?don：Oxford University Press，1994.

[3]Hedeker D,Gibbons D.Longitudinal Data Analysis[M].New York:John Wiley&Sons,2006.

[4]Wedderburn R W M.Quasi-likelihood Functions,Generalized Linear Models,and the Guass-Newton Method[J].Biometrika,1974,61(3).

[5]McCullagh P.Quasi-likelihood functions.The annals of statistics,1983,11(1).

[6]Crowder M.On the Use of a Working Correlation Matrix in Using Gen?eralized Linear Models for Repeated Measures[J].Biometrika,1995,(82).

[7]Qu A,Lindsay B G,and Li B.Improving Generalized Estimating Equations Using Quadratic Inference Functions[J].Biometrika,2000,(87).

[8]Han P S,Song Peter X.-K.A Note on Improving Quadratic Inference Functions Using a Linear Shrinkage Approach[J].Statistics and proba?bility letters,2011,(81).

[9]Wu H,Zhang J.Nonparametric Regression Methods for Longitudinal Data Analysis[M].New York：John Wiley&Sons,2006.