概率在日常生活和工作中的應用

鄭艷霞

（中國青年政治學院 經濟系，北京 100089）

和經典數學分支相比，概率是一門“年輕”的學科，這門學科到目前還有許多不完善的地方，但就它已得到的成果，已經給人類活動的諸多領域帶來了一場革命.這場革命也改變了人們的思維方法，如果我們運用概率的知識來重新分析和認識自己生活和工作中的問題，不但能對以往的經驗找到數學的理論依據，而且會得到與以往思維模式不同的答案，而理性的思維方式會讓我們變得更聰明，更有智慧.

1 只要功夫深，鐵杵磨成針——概率告訴我們持之以恒的力量

某人英語基礎薄弱，目前只有高中生的英語水平，工作需要他5年之后必須去英國，并且需要運用英語開展工作.可是他現在的工作十分繁忙，無法抽出大量的時間來集中學習英語，于是他制定了一份特殊的學習計劃——每天抽出30分鐘時間來學習英語.我們幫他分析一下，他5年后能夠運用英語工作的可能性有多大？

按照北京語言大學出國留學人員英語培訓的科目資料顯示：英語聽說讀寫全能業余班培訓初級班共需要120小時，中級班120小時，高級班120小時.按照該人需要達到中級班培訓合格的水平計算，每天30分鐘的時間學習英語知識對于實現目標的可能性非常小，僅僅為p=0.002083左右.設Ai={第i天學習成功}且Ai相互獨立,i=1,…,n.再設A={五年后能夠運用英語工作}，5年有 1825天，當 n=1825時，P(A)

若該人想要達到高級班培訓合格的水平，p=0.0014，P(A)=1-(1-p)n=92.24%.

由計算結果可以看出，只要此人每天堅持花30分鐘時間努力學習英語，這個人5年后能夠運用英語工作的可能性為97.84%，這幾乎說只要他每天堅持努力，5年后能運用英語工作是自然而然的事情；就是自如運用英語進行工作也有九成以上的把握.因此人要是想增加一件事情成功的把握，一個方面是增加事情本身成功的勝算，也就是增大p值.如果本身事情成功的勝算不大甚至于很小，只要堅持不懈的努力，也就是增大n的取值依然可以增大成功的可能性，而且長時間堅持不懈的努力，會把一件希望渺茫的事情變成必然.這也是對“只要功夫深，鐵杵磨成針”的最好詮釋.

2 三個臭皮匠，頂一個諸葛亮——概率告訴我們團隊合作的力量

常言道：“三個臭皮匠，頂一個諸葛亮”.這是對人多辦法多，集體力量大的一種贊譽，這也可以由概率的計算得到證實.假設三個臭皮匠能獨立解決某問題的概率分別為0.45，0.55，0.60,問三人合力能解決該問題的可能性是多少？

將三人編號為1,2,3,記Ai={第i個人能解決該問題}，i=1,2,3.解決上述問題關鍵是求P(A1∪A2∪A3).已知P(A1)=0.45，P(A2)=0.55，P(A3)=0.60，且 A1，A2，A3相互獨立，因此

看！三個并不聰明的臭皮匠，能以90%以上的概率解決問題，聰明的諸葛亮也不過如此嘛.可見團隊合作是非常重要的.由此可見，在一個團隊中，只要能夠集思廣益，把大家的優勢都發揮出來，力量比擁有幾個“智者”大得多.

3 未雨綢繆——概率指導我們科學看待體檢，防病治病

一項血液化驗有95%的把握將患者某種癌癥鑒別出來.但是，這項化驗用于檢測健康人也會有5%的人呈現陽性（即把健康人誤診為患癌癥的概率為5%）.如果該種癌癥的患者實際占人口的0.5%，而某人化驗結果是陽性，問此人患該種癌癥的概率是多少？如果某人化驗結果是陽性，該怎么辦？

我們首先分析如果某人的體檢結果呈陽性，他患有癌癥的風險有多大.假設A={化驗結果為陽性}，B={此人患該種癌癥}，B={此人健康}，由貝葉斯公式有

計算結果表明，若該人進行試驗且結果為陽性，則此人確實患癌癥的概率為P(B1|A)=0.087.也就是說即使檢查的結果呈陽性也不必過早下結論該人患有癌癥，這種可能性只有8.7%，即平均每1000人中大約只有87人確患有該種癌癥.但是這種試驗對于診斷一個人是否患有癌癥是有很大意義的.如果不做試驗抽查一人，他是患者的概率P(B1)=0.005；若作試驗且是陽性結果，則他是患者的概率為P(B1|A)=0.087，患癌癥的風險提高十七倍多，起到了很好的警示作用.

如果某人體檢結果顯示為陽性，在保持樂觀精神的同時提高對該種癌癥監測力度是必要的.下面用貝葉斯公式計算監測的用處.設 Ai={第 i次化驗結果為陽性，i=1，2，3}，B={此人患該種癌癥}，B={此人健康}，由貝葉斯公式有

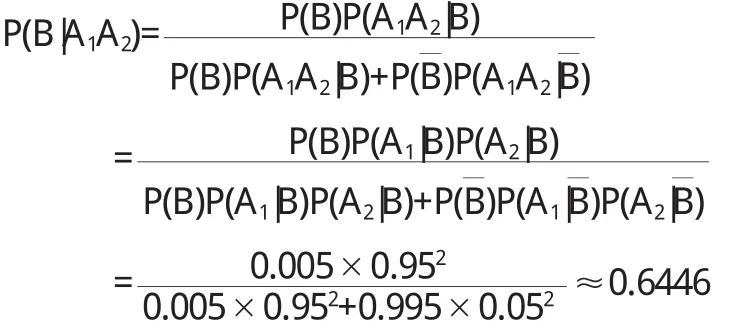
這說明體檢結果呈現陽性，隔一段時間再去監測，如果監測結果仍然是呈陽性的，此時患癌癥的風險已經過半，必須提高警惕了，應該在積極就醫的情況下保持良好心態并繼續進行監測.

再過一段時間再去監測，假如結果仍然呈陽性，幾乎可以肯定該人是患了癌癥，因為

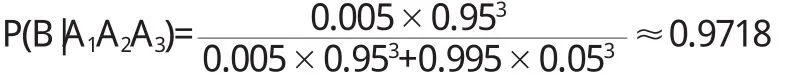
運用概率的知識讓我們能夠更加客觀的看待醫學檢查，既不是悲觀失望，被檢查結果嚇倒，同時又采取科學的態度進一步監測，用正確的方法指導就醫.

4 抓住真兇——概率給我們一雙“慧眼”，認清嫌疑犯

1981年3月30日，美國大學退學學生Hinckley企圖對里根總統行刺，他打傷了里根總統、里根總統的新聞秘書以及兩個保安人員.1982年，Hinckley因為犯有謀殺總統的罪名而被起訴，審判他時，Hinckley以精神病為理由為自己作無罪的辯護.Hinckley的辯護律師拿出Hinckley的CAT掃描作為證據爭辯說，因為Hinckley的掃描展示了腦萎縮，因而他患有精神病的可能性更大些.作證的醫師是Daniel R.Weinberger告訴法院當被診斷為精神分裂癥的人進行CAT掃描(計算機輔助層析掃描)時，掃描結果有30%的案例顯示為腦萎縮，而只有2%的正常人掃描顯示腦萎縮.最后在辯護人的有力辯護下，Hinckley被判無罪.那么辯護律師提供的關于腦萎縮證據足以說明Hinckley患有精神病嗎？

從表面上看，Hinckley辯護律師的辯護似乎很有說服力，能夠證實Hinckley是精神病患者.下面我們用概率的方法驗證一下辯護律師的結論.通過收集醫學資料可以知道，在美國精神分裂癥的發病率大約為1.5%.設事件A={腦萎縮}，B={患有精神病}，由貝葉斯公式有

計算結果表明，在Hinckley的CAT掃描結果是腦萎縮的前提下，他患有精神病的可能性只有18.6%，顯然辯護律師僅僅用CAT掃描結果是腦萎縮來證明Hinckley患有精神病，證據的說服力很弱，如果想證明Hinckley確實患有精神病，還應該提供其他更有力的證據才行.

由此可見，我們通常得到的一些結論在表面上看似乎很有道理，但是運用概率知識進行分析和計算，就會發現其實有些結果與我們的直覺是不一樣的.甚至可以得出截然相反的答案來.

5 “3σ原則”助力高考作文閱卷——概率讓感性的工作增加客觀公正的籌碼

“3σ原則”指的是，若隨機變量X服從參數為μ和σ2的正態分布，則P(|X-μ|<3σ)=0.9974.也就是說，如果隨機變量是服從參數為μ和σ2的正態分布，則隨機變量的1000個取值平均有997個以上分布在以μ為中心以3σ為半徑的區間內.也就是說，隨機變量取值非常大或者非常小都是很少的.

“3σ原則”在工業上普遍使用，現在其他行業也開始使用該原則，比如現在高考語文的作文評分中就使用了該原則.大家都知道，語文作文的評分很難，有的老師覺得這篇作文結構緊湊，文字優美就給出高分，甚至給出滿分，而同樣一篇作文假如換另外一位老師判卷，可能就是另外的分數，中間的分數差異可能很大，這就給考生的成績帶來不小的變化，而高考成績是決定人命運的大事，因此如何建立相對公平的給分體系，是教育專家們考慮的一個重要問題.由概率知識可知高考語文作文成績服從正態分布，于是引入概率統計中的“3σ原則”，來干預高考的語文作文閱卷工作.大致的作法是：請一批包括大學教授在內的最有聲望的作文老師團隊來判分，發現他們的分數判的比較準確、穩定，分數相差不多，因此用他們的分數作為統計數據來確定當年的作文分數的期望μ和方差σ2，給出當年高考作文的平均值及分數的波動的上下限來.在高考語文作文閱卷過程中，不斷檢查每位閱卷教師所給出的作文分數，如果閱卷老師給出的分數在允許的范圍之內就通過，認為閱卷老師給出的是合理的分數，否則馬上警告這一小組要小心，如果再出現一個奇異分數，就將該組試卷全部重判，甚至請專家組介入判卷過程，只有經過多人重復確定的奇異分數才會有效，以此保證給出的作文分數更加合理.“3σ原則”在高考語文作文判卷中的使用，對于極高或者極低分數的作文成績起到警戒作用，對于高考語文作文判卷這項主觀性很強的工作增加理性的衡量，對于判分的公平性起到了很好的作用.

6 免費抽獎問題——概率讓我們認清商家的促銷活動

某電子產品公司推出了一個非常有吸引力的抽獎活動：“本公司為了答謝廣大用戶長期以來的支持與厚愛，特別推出免費抽獎活動.抽獎方式為：箱子里有20張卡片，10張上標有數字10，另外的10個上標有數字5.從箱子里摸出10張卡片，把各卡片上的數字相加，按數字之和設置獎項如下：

?

“抽獎結果共有 11個，即 50、55、60、65、70、75、80、85、90、95、100分.其中有10個分數可免費得到獎品，中獎率超過90%”.

這樣的宣傳從直覺上非常有誘惑力，但是如果我們仔細觀察，就會發現實際上情況與我們想象的有很大的差異，顧客參加抽獎活動即便中獎也幾乎都是非常小的獎項，能夠中六等獎以上的獎項非常稀少，大部分中獎的顧客都是DVD盤盒，或者可以購買5折U盤.下面我們運用概率知識，詳細解讀商家的抽獎活動.

分析可知，這是一個超幾何分布，設Ai={抽出10張卡片中含有數字 10的個數}，i=0，1，2，……，10，則 P(Ai)=.經過計算可以得到中各種獎的概率如下

?

再進一步調查各種獎項的成本，得到下面的信息：

?

計算商家的平均收益為：

由此可見，這場看似熱鬧的抽獎活動，其實是商家促銷的一種手段.實際上商家在擴大自己的知名度、免費進行了廣告宣傳的同時還是穩賺不賠的.而商家宣傳的中獎率超過90%的概率只是迷惑顧客的方法.這11種情況出現的概率大小差別非常大，而通常我們會認為各種情況出現的可能性是均等的，商家借此概念的混淆來迷惑顧客.

由于隨機現象在現實世界中大量存在,概率越來越顯示出它巨大的威力.其實，我們日常生活中到處都有概率的影子，小到每天的天氣預報，大到航空母艦的制造，都離不開概率統計，在經濟活動和實際的生活中，有許多問題尤其是決策問題可以直接或間接地利用概率結論來解決，或者可以應用概率給出有價值的參考意見.

〔1〕鄭艷霞，鄧艷娟.高等數學基礎教程[M].北京：清華大學出版社，2010.

〔2〕中央電視臺《百家講壇》欄目組.相識數學[M].北京：中國人民大學出版社，2006.

〔3〕林志興.概率與直覺[J].數理統計與管理,2006(2)：240-243.