解并行機模糊調度問題的自適應遺傳算法

劉文程，高家全

解并行機模糊調度問題的自適應遺傳算法

劉文程，高家全

針對家紡企業車間調度的實際情況，建立了一種產品優先級約束的模糊車間調度模型。在模型中，完工時間和交貨期都是模糊的，交貨期平均滿意度最大為調度目標。基于此模型，提出了一種自適應的遺傳算法，該算法通過比例選擇及局部搜索保證種群的優良特性，并通過自動調節變異率和交叉率的方式保證種群的多樣性，有效跳出局部收斂。仿真結果表明，自適應遺傳算法能有效求解，并優于免疫遺傳算法。

并行機；模糊加工時間；模糊交貨期；模糊調度；遺傳算法

1 引言

家紡企業作為傳統的制造企業，在我國的制造業中具有舉足輕重的地位。現有的一些研究成果主要集中在對家紡企業確定性車間生產調度問題上[1-2]，但在家紡企業實際的生產過程中，不僅有確定性生產調度問題，還具有不確定性生產調度問題。不確定性的生產調度問題一方面是由家紡企業特殊的性能造成的，比如原料的不同特性，操作工人熟練度的差異，機器設備不同程度老化等，這都將影響產品的加工進度，并使得加工時間變得不確定；另一方面是由于同一批次的產品可能來自不同的訂單，不同的訂單的交貨期一般而言是不一樣的，這就將使得產品的交貨期不同。

現階段，在車間調度領域針對不確定的生產調度問題的研究，已有一些研究成果[3-12]。這些研究一般針對模糊車間調度問題，大部分是對模糊的加工時間或模糊的交貨期這種單一情況下的作業車間的模糊調度問題進行研究。盡管也有部分學者對模糊加工時間和模糊交貨期這種較為復雜的情況進行研究，但是他們對滿意度函數的考慮存在一定的偏差，沒有考慮到對于企業而言，不同客戶的重要程度是不相同的，這樣將使得調度結果不合理。從而使得家紡企業的生產調度問題無法應用已有的研究成果，需要專門針對其生產特點進行研究。

本文根據家紡企業在實際生產調度過程中所具有的特點，分別對加工時間和交貨期進行模糊化處理，在此基礎上建立模糊化的生產調度模型，并提出一種改進的自適應遺傳算法。該算法能夠通過調整變異率和交叉的方式保證種群的多樣性，并能夠有效跳出局部收斂；仿真結果證實了該算法的有效性和可靠性。

2 模糊生產調度模型

2.1 問題描述

家紡企業的模糊生產調度模型一般可以簡單描述為：數量為n的產品在m臺機器上分別進行加工，產品分別來自不相同的訂單，訂單來自不同的客戶，因此具有不同的優先級。每個產品都具有模糊的加工時間及與客戶滿意度相關聯的模糊交貨期，產品的加工操作必須滿足一定的工藝約束，即不是所有的產品都可以在任何機器上進行加工。每個產品在進行加工時，只能在一臺機器上進行一次加工并完成產品的加工操作。產品的加工操作在機器上開始進行后，直到產品完成加工之前不能停止產品的加工，中途機器不能對其他產品進行加工，即機器同一時刻只能對一個產品進行加工操作。家紡企業調度的目標是尋找一種可行的方案，使得這種方案既能滿足企業特定的工藝要求，又能使得調度目標獲得最優解。

2.2 變量描述

為了方便敘述，引入下面的記號。

p?ij：模糊加工時間。即為產品 j在機器i上的加工時間，其中包括對產品配件進行裝配的時間、傳輸產品的時間、卸載產品時間、加工產品時間及對產品進行清洗的時間等，是在一定區間變化的模糊變量，用三角模糊數表示，為加工時間樂觀值，為加工時間可能值，為加工時間悲觀值。

Ωj：所有能加工產品 j的機器集合。

c?j：產品 j的模糊完工時間。這是由產品的加工時間的模糊性決定的，模糊的加工時間必然導致模糊的完工時間。

AI：平均面積滿意度。

t?ij：產品 j在機器i上的開始加工時間。

λj：產品的優先級系數。

設決策變量：

2.3 數學模型

平均滿意度最大模型：

圖1 模糊的完工時間和交貨期滿意度

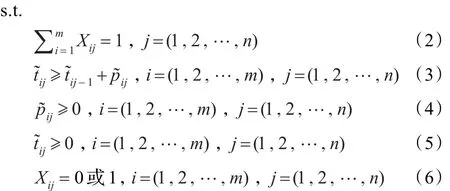
式（1）是問題的目標平均滿意度最大；式（2）～（6）是滿足目標函數的約束項，依次分別表示為：產品只能夠在一臺機器上進行加工；機器同一時刻只能加工一個產品，即只有在完成一個產品的加工后，才能開始下一產品的加工；產品在各機器上的加工時間均非負值；產品在各機器上的開始加工時間均非負值；決策變量的取值范圍。

3 算法設計

根據家紡企業的實際情況，建立了不確定性生產調度模型，為了對該模型進行求解，設計了一種自適應性的遺傳算法。算法基本流程如圖2，具體步驟如下：

步驟1將初始種群的規模設定為NG，根據約束條件隨機產生初始種群。

步驟2根據采用的適應度函數來計算每個染色體的適應度值。

步驟3運用比例選擇機制以及最優保存策略對下一代種群的染色體進行選擇。

步驟4讓種群中的染色體兩兩進行交叉，交叉率根據種群的收斂情況進行調整，當種群快速收斂時，適當減小交叉率，當種群趨于發散時，適當增大交叉率，通過控制交叉率來實現對種群收斂速度的控制。

步驟5讓種群中的染色體進行變異，變異率同樣根據種群的收斂情況進行調整，當種群快速收斂時，適當提高變異率，當種群趨于發散時，適當減小變異率，通過控制變異率來保證種群的多樣性和染色體的優良特性。

步驟6局部搜索算法對種群進行優化，使種群保持優良特性。

步驟7重復步驟2到步驟6，當滿足設定的終止條件時停止。

3.1 編碼設計及適應度函數

向量組編碼方式解碼簡單且能方便地執行遺傳操作，更具有不會產生無效個體的優點，因此本算法采用向量組的編碼方式進行編碼。

適應度函數是作為一種標準用來區分種群中染色體優劣的，一般通過變換原適應度間的比例關系來調節適應度值。對于2.3節中模型的目標函數，這里采用的適應度函數為：

由式（7）可知，分母是固定的值，因此分子越大，則適應度的值越大。

圖2 自適應遺傳算法流程圖

3.2 選擇算子

采用比例機制選擇相應個體，通過輪盤賭選擇方法對正比于個體適應度的概率進行計算。再經過多輪選擇，選出需要進行交配的個體。每一輪選擇時，首先均勻產生一個[0，1]的隨機數，然后將該隨機數作為選擇指針，對比各個染色體的相對適應度來確定被選中的染色體。若種群的大小為N，染色體i的適應度值為 fi，那么染色體i被選擇的概率Pf為：

本文算法不僅采用比例機制，同時將每代的最優染色體進行保存。通過用最優的染色體替換掉適應度值最低的染色體的方式，來提升種群的優良特性。

3.3 交叉算子

本文算法針對向量組編碼方法，在部分匹配交叉的基礎上提出了一種隨機擴展交叉算子。具體過程如下：

（1）產生一個正整數n，在染色體長度的30%～50%之間進行隨機選取。交叉的基因位數將由正整數n來決定，比如n的大小為3，那么染色體中將有三位基因進行交叉。

（2）隨機產生數量為m的正整數作為需要交叉的基因點。

（3）假設需要將染色體A、B進行交叉，選取染色體A中的基因放入染色體B中的前面，并刪除染色體B中相同的基因，從而產生基于染色體B的新染色體。同時，將染色體B中選取的基因放入染色體A中的前面，并刪除染色體A中相同的基因，從而產生基于染色體A的新染色體。

下面通過舉例說明染色體的交叉過程，假設需要交叉的染色體A、B分別為：

假設n=3，隨機產生的基因位分別為4，8，2，那么經過交叉后獲得的新染色體分別為：

將新染色體中相同的基因位分別進行刪除后，便可獲得分別基于染色體A、B的后代染色體：

3.4 變異算子

本文算法的變異方式通過多點插入的形式來實現，這一方式適合向量組編碼的特性。下面對這一方式進行說明，先對要變異的基因位gi進行隨機選擇，再變換gi中第二行的機器號，在每次變換機器后對染色體的適應度值重新計算并做保留。當完成對所有可選機器的插入計算后，選擇出最優的染色體作為變異產生的染色體。這種變異方式在保留父代信息的同時，保證了變異后的染色體的質量。

3.5 局部搜索算法

局部搜索算法一方面加快了種群搜索速度，另一方面提高了種群的質量，優化了算法性能。具體算法步驟如下所示。

對種群中的每一個染色體u進行如下操作：

（1）對u進行反轉變異，將產生的染色體記為u*；

（2）評價u和u*；

（3）若u*優于u，則u=u*；

（4）若搜索次數達到設定的搜索次數，則停止搜索，否則重復（1）～（3）。

3.6 自適應技術

動態自適應技術通過調整遺傳算法控制參數來控制種群的優化，即在種群的進化過程中根據種群收斂情況對Pc、Pm的數值進行適當調整。具體做法為：若種群趨于收斂，則在減小Pc的同時增大Pm，即通過將交叉的概率降低的同時將變異的概率提高來保證種群的多樣性，以避免種群早熟；若種群發散，在在增大Pc的同時減小Pm，即通過將交叉的概率提高的同時將變異概率降低來加快算法的收斂速度。

在種群的進化過程中，σ為兩代種群最優值的差值，通過讓交叉概率Pc和變異概率Pm跟隨σ的變換而變化來達到對種群優化過程的控制，使種群的Pc、Pm值能根據σ動態調整。數學描述如下：

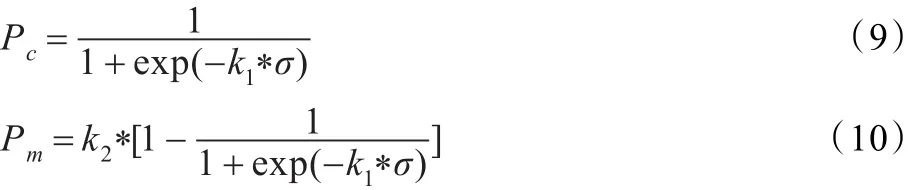
4 仿真及實驗分析

在型號為華碩X81SG的計算機上，操作系統為Windows XP，在C++Builder軟件環境下采用C++語言對全部算法進行編寫。隨機產生每種產品的機器集合、對應加工時間和交貨期，使其滿足均勻分布的要求。

4.1 對模糊完工時間仿真

通過對產品為15，加工機器為4的家紡企業生產調度問題進行仿真示例，來驗證本文提出的AGA算法的可行性。表1為算例的具體模糊加工時間，表中縱排為產品號，橫排為機器號，表格中的三個數字分別對應樂觀值、最可能值和悲觀值。

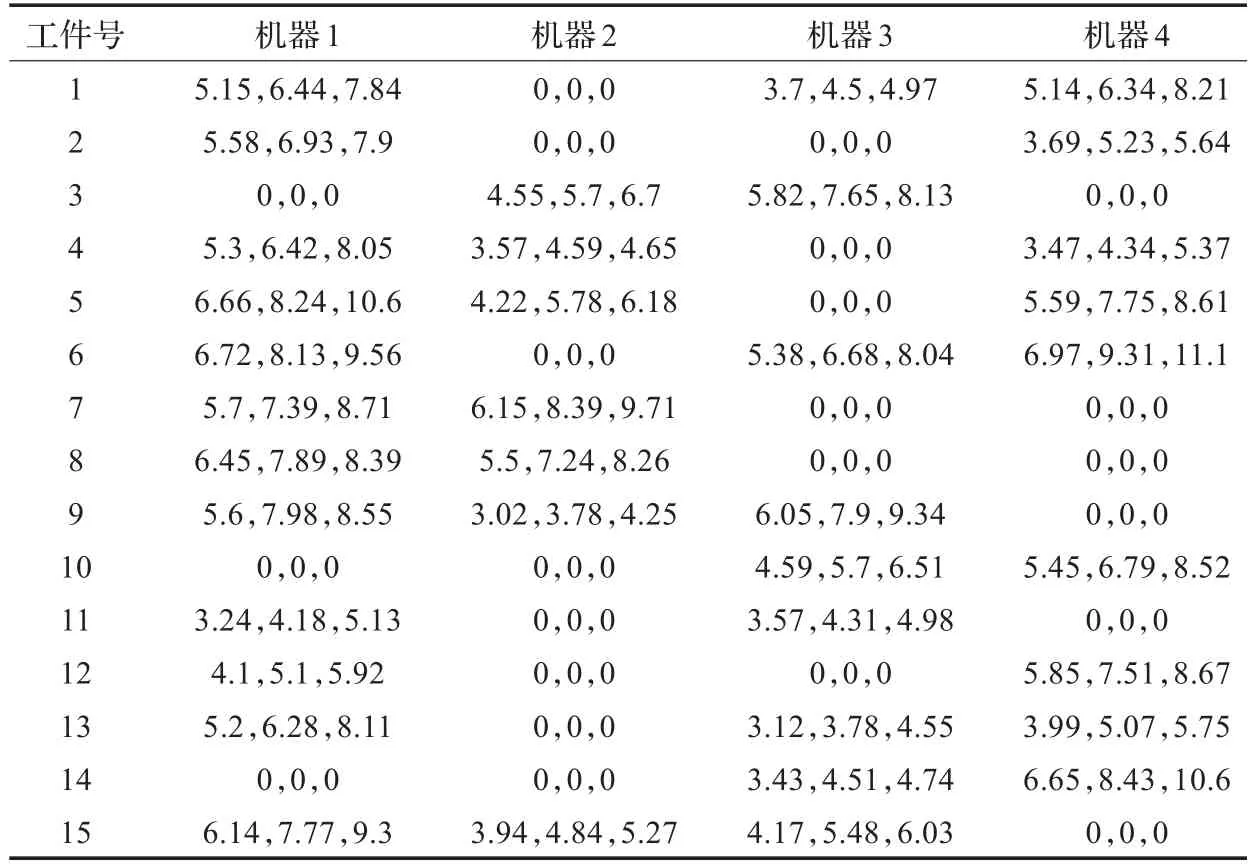
表1 15工件4機器模糊加工時間表

表2為產品模糊交貨期和優先級表。設定在提前交貨的情況下客戶的滿意度為1，即只要模糊完工時間能在模糊交貨期之前，那么不會對客戶的滿意度造成影響。不同優先級的產品所具有的優先級系數是不相同的，這里設定優先級為1和優先級為2的產品的優先級系數分別為1和1.2。

表2 產品模糊交貨期和優先級表

設置自適應遺傳算法的參數，種群數量設為50，局部搜索交換次數設為20，參數k1設為300，k2設為0.1，交叉率和變異率的變化區間分別為0.5～1.0和0～0.05。

仿真可得最優染色體為：

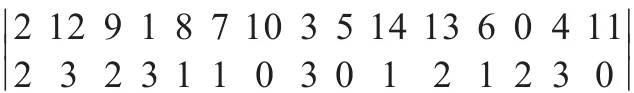
通過對最優染色體分析可得，高優先級客戶產品的交貨期能夠獲得高滿意度，一般能夠達到1；普通產品的交貨期也能獲得不低的滿意度，保證在0.95以上。這證明AGA算法能有效求解問題模型。

4.2 對比實驗

為驗證本文提出的AGA算法的有效性，與文獻[4]提出的克隆選擇算法（CAS）和文獻[7]提出的人工免疫算法（AIS）進行比較。以客戶滿意度最大為目標，分別對模糊數據規模為30×10，60×10，80×15和100×10的數據進行仿真，數據結果由算法進行10次運算，然后取其中的最優值并計算出平均值。

表3 算法比較結果

由表3可知，AGA算法的性能要優于CAS算法和AIS算法。針對不同規模的問題，在迭代次數相同的情況下，AGA算法的最優值要優于CAS算法和AIS算法，而且隨著問題規模的增加，AIS算法和CAS算法取得的最優值跟全局最優值的差距變大，而AGA算法依然能取得全局最優值或接近全局最優值，說明算法能夠跳出局部最優達到全局最優值，從而說明本文提出的AGA算法性能要優于AIS算法和CAS算法。

5 結束語

本文針對并行機模糊調度問題，根據客戶滿意度最大這一生產目標，建立了模糊生產調度模型，并構建了自適應遺傳算法對其進行求解。該算法能夠克服一般遺傳算法趨于局部最優的缺點，提高了全局尋優能力。與AIS算法和CAS算法進行對比實驗，仿真結果表明該算法具有更優的性能。

[1]高家全，趙端陽，何桂霞，等.解特殊工藝約束拖后調度問題的并行遺傳算法[J].計算機工程應用，2007，43（27）：184-186.

[2]劉文程.家紡企業生產調度模型及優化算法研究[D].杭州：浙江工業大學，2009.

[3]沈兵虎，柳毅.改進微粒群算法求解模糊交貨期Flow-shop調度問題[J].計算機工程與應用，2006，42（34）：36-38.

[4]Ong Z X，Tay J C，Kwoh K C.Applying the clonal selection principle to find flexible job-shop schedules[C]//Proceedings of the 4th International Conference on Artificial Immunes Systems，2005：442-455.

[5]Masatoshi S.Fuzzy programming for multiobjective job shop scheduling with fuzzy processing time and fuzzy duedate through genetic algorithms[J].European Journal of Operational Research，2000，120（2）：393-407.

[6]雷德明，吳智銘.多目標模糊作業車間調度問題研究[J].計算機集成制造系統，2006，12（2）：174-179.

[7]Agarwal R，Tiwari M K，Mukherjee S K.Artificial immune system based approach for solving resource constraint project scheduling problem[J].International Journal of Advanced Manufacturing Technology，2007，34：584-593.

[8]李富明，朱云龍.可變機器約束的模糊作業車間調度問題研究[J].計算機集成制造系統，2006，12（2）：169-174.

[9]柳毅，葉春明.模糊交貨期Flow-shop調度問題的改進微粒群算法[J].哈爾濱工業大學學報，2009，41（1）：145-148.

[10]Tang J，Zhang G，Lin B，et al.A hybrid algorithm for flexible job-shop scheduling problem[J].Procedia Engineering，2011，15：3678-3683.

[11]Wang L，Tang D.An improved adaptive genetic algorithm based on hormonemodulation mechanism forjob-shop scheduling problem[J].ExpertSystemswith Applications，2011，38（6）：7243-7250.

[12]Ren Q，Wang Y.A new hybrid genetic algorithm for job shop scheduling problems[J].Computer and Operations Research，2012，39（10）：2291-2299.

LIU Wencheng,GAO Jiaquan

浙江工業大學 之江學院，杭州 310024

College of Zhijiang,Zhejiang University of Technology,Hangzhou 310024,China

According to the practical job shop scheduling problem subject to priority constraint of products with fuzzy processing time and due time in textile manufacturing industry,a scheduling model with maximization of average satisfaction is proposed. Furthermore,an Adaptive Genetic Algorithm（AGA）is presented to solve the scheduling models.In this algorithm,besides the proportional selection,the self-adapting mutation and cross are proposed to enhance the diversity of the population.Simulation results show that AGA is effective and is advantageous to the artificial immune algorithm.

parallel machines;fuzzy processing time;fuzzy due-date;fuzzy scheduling;Genetic Algorithm（GA）

A

TP301

10.3778/j.issn.1002-8331.1210-0090

LIU Wencheng,GAO Jiaquan.Self-adapting genetic algorithm for solving fuzzy scheduling problem on parallel machines. Computer Engineering and Applications,2013,49（7）：60-63.

浙江省自然科學基金（No.LY12A01027）。

劉文程（1984—），男，碩士，研究領域為生產調度優化，算法優化；高家全（1972—），男，博士，副教授，研究領域為智能優化算法及其應用，高性能計算。E-mail：lwc198411@126.com

2012-10-10

2012-12-27

1002-8331（2013）07-0060-04