一種稀疏自適應的正交互補匹配追蹤算法

郭永紅，楊毅彬

一種稀疏自適應的正交互補匹配追蹤算法

郭永紅，楊毅彬

針對實際應用中信號稀疏度未知的缺點，提出了一種稀疏度自適應的正交互補匹配追蹤算法。算法先初始化稀疏度，再通過互補正交匹配追蹤重構信號，找到一個支撐集；若支撐集不滿足條件，則按指定步長增加稀疏度，再次運用算法進行重構，直到支撐集滿足條件，得到最優支撐集。實驗結果表明，該算法可以準確有效地重構信號，并且在相同壓縮比下，其重構質量（PSNR）優于其他幾種算法。

稀疏度；正交互補；指定步長；支撐集

1 引言

Nyquist采樣理論在傳統的信號理論中起著關鍵作用，它要求采樣頻率須為信號帶寬的兩倍。壓縮感知理論（Compressed Sensing，CS）[1-2]表示如果信號在某個變換域上稀疏，則可將信號投影到一個低維空間，然后利用投影值通過求解范數最優化問題，可高概率地精確重建原始信號。CS理論表明恢復信號所需要的采樣數據遠低于Nyquist定理所定義的采樣量，因此該理論一經出現就引起國內外相關領域研究人員的密切關注。設信號x(x∈RN) 為N×1維列向量。若 x中僅有不超過k(k＜＜N)個非零元素，則x稱為k-稀疏信號。用一個M×N(M＜＜N)維的測量矩陣對信號進行投影，即 y=Φx，則基于 y可對信號進行重構。

在已知 y和Φ的條件下對信號x進行重構是CS研究的一個重要方面。目前重建算法主要分為兩類：一類是基于l1范數最小化的凸優化算法，主要包括基追蹤算法（Basis Pursuit，BP）[3]、梯度追蹤算法（Gradient Pursuit，GP）[4]、內點迭代法等；另一類是基于l0范數最小化的貪婪算法，主要包括匹配追蹤（Matching pursuit，MP）[5]、正交匹配追蹤（Orthogonal Matching Pursuit，OMP）[6]、互補匹配追蹤（Complementary Matching Pursuit，CMP）[7]、正交互補匹配追蹤算法（Orthogonal Complementary Matching Pursuit，OCMP）[8]、正則化正交匹配追蹤算法（Regularized Orthogonal Matching Pursuit，ROMP）[9]等。貪婪算法由于結構簡單，運算量小等特點得到應用。但這幾種算法均要求信號稀疏度已知，這在很多實際應用中很難滿足，如果對稀疏度的估計不準確，信號將不能得到精確重建。針對實際信號中稀疏度未知的特點，本文結合文獻[10]提出的自適應匹配追蹤算法（Sparsity Adaptive Matching Pursuit，SAMP），提出一種稀疏度自適應的迭代算法，采用增加固定原子的方法來估計稀疏度。

2 正交互補匹配追蹤算法

文獻[7]互補匹配追蹤算法（CMP）類似于經典匹配追蹤算法（MP），與其不同的是CMP算法是直接在原信號x的行空間上求解。每次迭代時，MP算法是從字典矩陣中選擇一個最匹配的原子；CMP則是剔除(N-1)不匹配的原子并保留剩下的一個最匹配的原子，這種方法使其具有比MP算法更好的重建效果。

文獻[8]提出的正交互補匹配追蹤算法（OCMP）是CMP的改進算法。OCMP算法在選擇原子上與CMP一樣，稀疏估計時采用最小二乘法對信號進行估計，算法步驟如下：

（1）初始化殘差r0=b，感知矩陣Φ=A+A，測量向量x2=A+b，對角矩陣Δ，其對角元素為：

其中A+=AT(AAT)-1為A的偽逆。

（2）計算相關性h，并尋找h中絕對值最大的元素：

（3）信號稀疏估計并更新殘差：

其中，I表示h中元素最大值的索引值構成的集合；當殘差r滿足停止條件時，迭代停止。

從上文可以看出，算法主要分為三個部分：計算相關性；更新索引集；更新殘差。算法在每次迭代時只找到信號的一個元素，對于稀疏度為k的信號，至少需要進行k次迭代才能恢復出原信號。如果稀疏度的估計不夠準確，那么估計信號的誤差將會很大。

3 改進算法

在實際生活中信號稀疏度往往未知，針對于此，本文提出了一種自適應迭代算法——稀疏自適應正交互補匹配追蹤算法（Sparsity Adaptive Orthogonal Complementary Matching Pursuit，SAOCMP）。主要思想是先初始化稀疏度，其值隨指定步長進行增加，然后對算法進行迭代，每次迭代都會找到信號的一個支撐集，再利用回溯思想更新上一次找到的支撐集，直至找到最終支撐集，從而達到重構信號的目的。本文算法框圖如圖1。

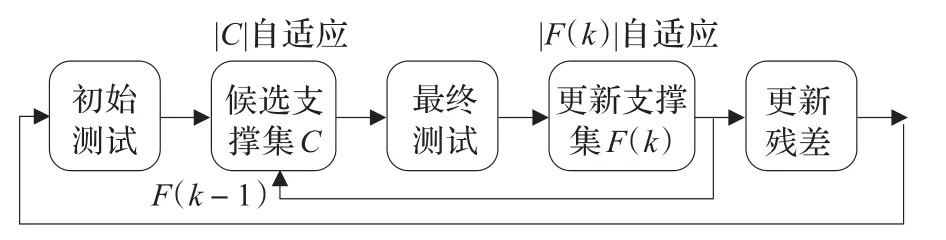
圖1 算法框圖

根據框圖，下面對算法的步驟進行具體闡述。

3.1 算法步驟

（1）算法輸入：字典矩陣A，測量向量s。初始化殘差值r0=s，迭代誤差δ，重構向量re_x，感知矩陣Φ=A+A，測量向量x2=A+s，對角矩陣Δ，其對角元素為：

步長step=1，信號支撐集Fk=[]。

（2）初始測試：計算第k次迭代的相關性，并找出前step個最大值S：

（3）候選支撐集C：

（4）最終測試：估計信號并求出前step個最大的元素Fk：

其中，ΦC為候選支撐集C對應的感知矩陣Φ的列向量組成的矩陣。

（5）計算殘差rk：

（6）若norm(rk)≥norm(rk-1)，則i=i+1；step=i×stage，返回步驟（2），否則直接返回步驟（2）。其中stage為固定步長。

（7）當估計信號與原始信號的差值小于迭代誤差δ時，則迭代停止。輸出重構向量re_x，滿足：

3.2 信號重建實驗

本實驗對CMP、OCMP、SAOCMP、CMP-OMP算法進行一維仿真，比較各個算法的相對誤差和運行時間。實驗測試當M=128，稀疏度k和采樣點數M取不同值時算法運行的結果。SAOCMP中初始步長step=1，終止條件為估計信號與原始信號殘差能量小于δ=e-12；算法在Pentium Dual-core E5400機器上運行，軟件版本為Matlab R2008a。對于不同的值，算法運行100次來計算平均重構誤差和平均運行時間。

圖2表示不同采樣點下信號準確重構率。從圖中可以看出本文算法在收斂速度是最快的，即在相同的準確重構率下，SAOCMP算法所需的采樣點數是最小的。對于重建誤差，當各個算法取相同采樣點時，SAOCMP算法與CMP、OCMP、CMP-OMP算法相比，其誤差是最小的，如表1所示。

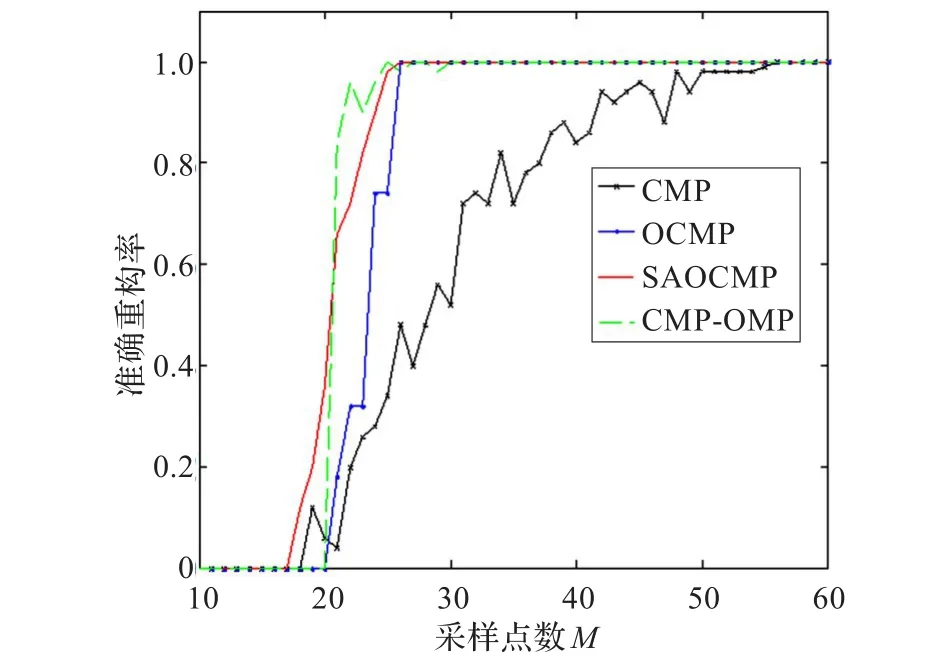
圖2 準確重建率對比分析

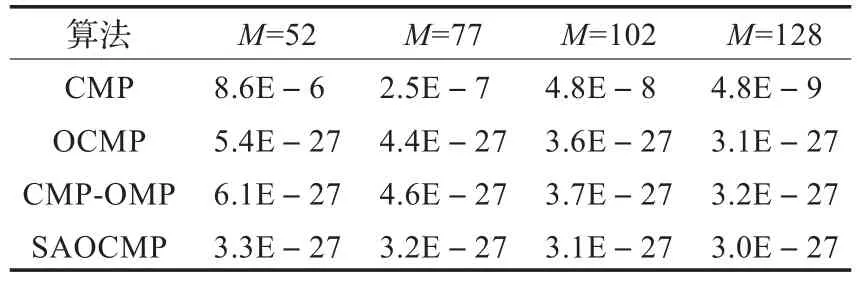
表1 不同采樣點數下重建誤差比較

圖3是在稀疏度相同、采樣點數不同的情況下重建信號的平均運行時間。從圖中可以看出，當M大于30時，SAOCMP算法的運行時間要小于OCMP。從重建誤差角度來分析，當各個算法取相同稀疏度時，與OCMP、CMP、CMP-OMP算法相比，SAOCMP算法具有重建誤差最小的優點，如表2所示。

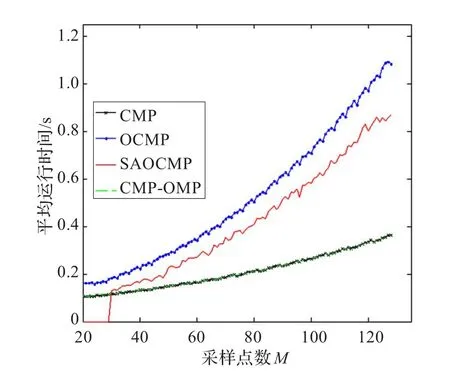
圖3 運行時間對比分析

表2 不同稀疏度下重建誤差比較

4 圖像實驗

實驗采用256×256像素的Lena圖像，采樣矩陣為隨機采樣矩陣，SAOCMP算法中步長stage=2。實驗比較了各個算法重建的運算時間、均方誤差MSE和峰值信噪比PSNR。圖4給出了壓縮比M/N=0.5時CMP、OCMP、SAOCMP、CMP-OMP算法的重建效果。由圖可見在壓縮比相同的情況下，SAOCMP算法的圖像重建效果要比其他算法更好。表3給出了不同算法重建圖像的運算時間、均方誤差MSE和峰值信噪比PSNR。從表中可以看出，當各算法具有相同壓縮比時，SAOCMP的PSNR最大，MSE最小。從運行時間角度分析，該算法犧牲了時間而獲得了更低的重構誤差，因此如何在保持低誤差的情況下減少運行時間是今后研究的方向。

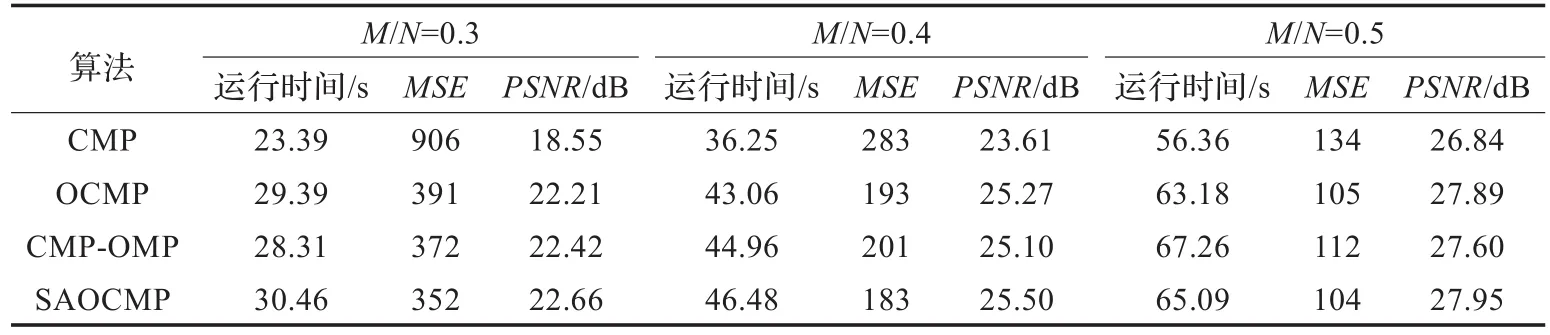
表3 各算法重建時間與性能比較

圖4 各算法重建圖像對比（M/N=0.5）

5 結論

本文提出了一種新的壓縮感知信號重構算法——稀疏自適應正交互補匹配追蹤算法。通過初始化稀疏度，并且在每次迭代后隨指定步長增加，利用回溯思想不斷估計和更新支撐集，直至滿足迭代停止條件為止。

實驗結果表明，本文算法可以在稀疏度未知的先驗條件下重建信號，并且能夠保證重建的準確率，同時減少了運行時間。經實驗證明，本文算法的重建質量無論是一維信號還是二維圖像上都優于現有同類算法，是一種重建效果較好的方法。

[1]Donoho D L.Compressed sensing[J].IEEE Trans on Inform Theory，2006，52（4）：1289-1306.

[2]Candes E J.Compressive sampling[C]//Proceedings of InternationalCongresson Mathematicians.Zurich Switzerland：European MathematicalSociety Publishing House，2006：1433-1452.

[3]Chen S B，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing，1998，20（1）：33-61.

[4]Blumensath T，Davies M E.Gradient pursuit[J].IEEE Trans on Signal Process，2008，56（6）：2370-2382.

[5]Mallat S，Zhang Z.Matching pursuits with time-frequency dictionaries[J].IEEE Trans Signal Process，1993，41（12）：3397-3415.

[6]Tropp J，Gilbert A.Signal recovery from random measurements viaorthogonal matching pursuit[J].IEEE Trans on Inform Theory，2008，53（12）：4655-4666.

[7]Rath G，Guillemot C.A complementary matching pursuit algorithm for sparse approximation[C]//Proceedings of European Signal Processing Conference，Aug 2008.

[8]Rath G，Guillemot C.Sparse approximation with an orthogonal complementary matching pursuitalgorithm[C]//Proceedings of IEEE International Conference on Aconstics，Speech and Signal Processing，2009，3：3325-3328.

[9]Needell D，Vershynin D.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics，2009（3）：317-334. [10]Do T T，Lu G，Nguyen N，et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]// Proc Asilomar Conference on Signals，Systems and Computers，Pacific Grove，California，2008，10：581-587.

GUO Yonghong,YANG Yibin

電子科技大學 電子科學技術研究院，成都 611731

Research Institute of Electronic Science and Technology,University of Electronic Science and Technology of China,Chengdu 611731,China

A novel sparsity adaptive orthogonal complementary matching pursuit algorithm is proposed when the sparsity is unknown.Signal is reconstructed by complementary orthogonal matching pursuit through initializing the sparsity,and a signal support can be determined.If the condition is not be reached,the sparsity is increased with specified steps,and the algorithm is re-used to reconstruct signal.The algorithm terminates when the condition is reached and the support is founded.Experimental results show that signal can be reconstructed accurately and effectively.Meanwhile,the proposed algorithm exhibits its superiority over other algorithms with the same compressed ratio.

sparsity;orthogonal complementary;specified steps;support

A

TN850.6；TP753

10.3778/j.issn.1002-8331.1108-0281

GUO Yonghong,YANG Yibin.Sparsity adaptive orthogonal complementary matching pursuit algorithm.Computer Engineering and Applications,2013,49（7）：144-146.

郭永紅（1987—），男，碩士研究生，主要研究方向為電子與通信工程；楊毅彬（1982—），男，助理研究員，主要研究方向為電磁場理論及其應用。E-mail：guoyonghong52400@163.com

2011-08-22

2011-10-17

1002-8331（2013）07-0144-03