基于RBF神經網絡的三基色配比研究

文蒸肖輝

(同濟大學電子與信息工程學院，上海 201804)

1 引言

色溫 (CT，color temperature)和顯色指數(CRI，color rendering index)是光源評價的重要指標，都是在三基色原理的基礎上進行的計算。目前光源色溫的計算已有相關研究［1］～［5］，但各種算法的預測精度存在不同程度的誤差，所需數據相當龐雜，計算量也很大，對于不同使用者而言，這些算法選擇性較大，可操作性太隨意，同樣的，顯色指數的計算研究也存在這方面問題［6］、［7］，其所需的參照樣板的數據表更是龐大。更為重要的是，色溫和顯色指數的計算是分開計算的，采用兩套算法的，對于計算機編程或者單獨計算，都是一件繁重、要求一定數學功底的任務。

因此，有人提出建立相應的數據庫，體現在RGB光源方面，殷錄橋等人在實驗中測試得到一個不同色溫配比的數據庫，實際色溫與理論計算相差無幾，基本實現了類太陽光動態色溫變化趨勢［8］;彭浩等人［9］依托 Matlab軟件建立了顯色指數的計算模型，只需輸入參與合成的單色光源光譜就可以計算出合成后光源的顯色指數。但是兩者的研究還只是基于原有算法的計算機化的結果，因此，前期的數據輸入仍然相當龐大，基于此，針對RGB-LED光源的光譜功率分布構成的特殊性，本文提供一種RBF神經網絡建立三基色配比和色溫、顯色指數之間的網絡模型，試圖將兩者聯系起來，使得一組配比產生兩個結果，同時還兼具簡單的特點，通過Matlab軟件仿真，驗證了該網絡模型精度高，具有很好的預測性能，可以用于實際需要。

2 徑向基函數神經網絡

徑向基函數神經網絡 (Radial Basis Function Neural Network，RBF)是人工神經網絡的典型結構，它是一種三層前向逼近網絡，即包含有一個輸入層、一個隱含層和一個輸出層，如圖1所示 (圖中的m、n和k表示相應層次的節點數目)，具有結構簡單、學習速度快、網絡模型能夠用數學式子表達等優點;而且，它是一種通用逼近器，能夠以任意精度逼近待求解預測模型［10］、［11］，特別適合于預測數據少的問題。

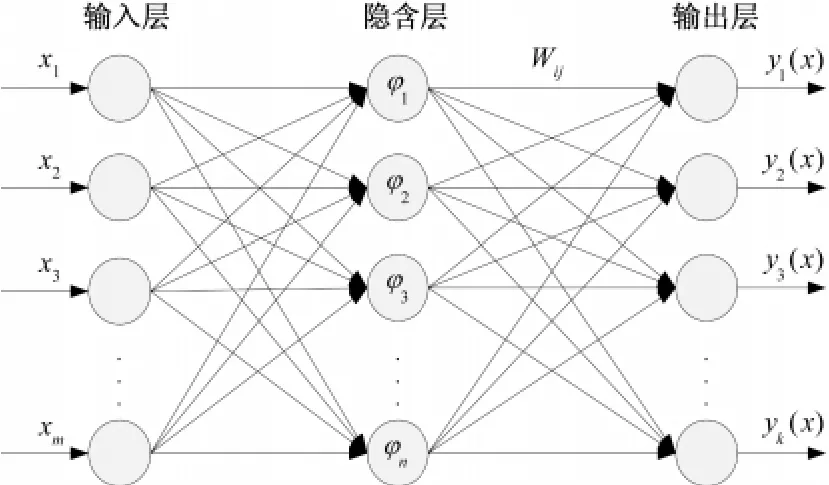
圖1 RBF網絡結構Fig.1 RBF neural network structure

在RBF網絡中，隱含層是由一組徑向基函數構成，隱含層節點通過基函數執行一種非線性變化，將輸入空間映射到一個新的空間，輸出層節點則在該新的空間實現線性加權組合，從而建立非線性問題的數學模型。具體結構和參量如下:假定X=(x1，x2，x3…xm)為輸入向量，Y=(y1，y2，y3…yk)是輸出向量，且Wij是隱含層到輸出層之間的權重值，其下標表示第i個隱含層節點到第j個輸出節點的連接權重;φi是關于n維空間的一個中心點具有徑向對稱的基函數，基函數的目的就是將低維的線性不可分的問題轉化成高維空間內線性可分，以逼近任意非線性函數。

研究發現，我們采用什么樣的徑向基函數，對RBF神經網絡函數逼近的性能幾乎沒有多大的影響［12］，同時由于高斯函數形式簡單，對于任意階導數光滑性能優越，廣泛用于各種情況下的函數逼近，即

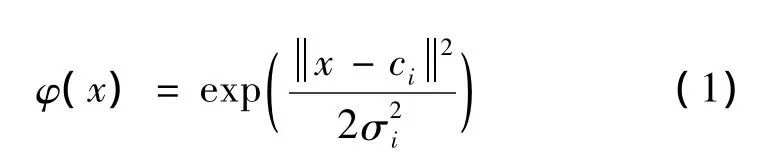
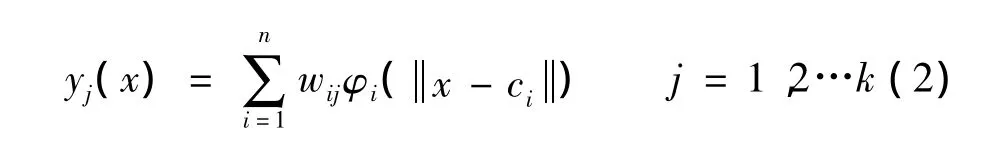
式中 k——輸出節點數;

n——隱含層節點數。

在實際應用中，網絡的各種參數都是通過一定的樣本進行學習得出的，這樣，輸入和輸出之間的關系就可以數學表達式表示出來。

因此，要獲得理想的RBF神經網絡模型，需要確定一下幾個方面:

①確定樣本的選擇。選擇實際測量的正確樣本，且樣本數據分布具有均衡性，這樣才能正確反映所要確立模型關系的內在規律，充分照顧到各個情況下的規律性特征，從而建立具有廣泛適用性的模型關系。基于神經網絡算法的特點，樣本的規模決定了網絡訓練結果的精度，而樣本規模只影響訓練的時間，所以樣本規模只需滿足實際需求即可。

②確定隱含層的結構。隱含層的節點數直接決定了RBF網絡的擬合程度［12］，數目過多會降低泛化能力，即用較少的樣本數據進行訓練，使神經網絡對樣本數據之外的輸入也能給出合適的輸出，容易產生過擬合，相反又會造成誤差太大，不利于預測，所以隱含層節點數目是關鍵。目前還沒有統一的方法來確定節點的數目，對于小規模的樣本，隱含層的節點數常可以取值等于基函數中心數［13］。

③確定的函數參數有三個，分別是:RBF的中心和擴展常數以及輸出神經元的權值。對于中心的選擇，并沒有統一的標準。一種常用的方法是根據經驗選擇中心，但對樣本的分布均勻性要求很高，中心一旦確定，就不再發生改變，但算法無法判斷樣本是否選取合理;另一種就是采用聚類的方法來選擇中心，有硬C均值算法、k-means算法以及最近鄰聚類學習算法等。而擴展常數的大小和中心數往往成反比關系，該數值過小，就需要許多的神經元來適應，這樣一來，設計的網絡性能就會很不好，因此，最好的方法就是采用尋優的方式尋找合適的基函數擴展常數。而隱含層到輸出層的線性關系中的權值有多種算法:梯度下降迭代法，偽逆法和最小二乘法等，但常用最小二乘法求解［14］、［15］。

3 三基色配比到色溫、顯色指數的RBF神經網絡的模型確定

就目前的RGB-LED來說，商業應用的LED芯片或激發熒光粉后產生的藍、黃綠和紅光的峰值波長大多分別落在420～490、500～580和590～660nm區域，按照CIE顯色指數計算方法，光源的顯色指數與光譜功率分布密切相關，對于RGB-LED來說，單色LED的峰值波長是光譜功率分布的決定因素，不同的峰值波長的疊加會產生不同的光譜分布。一般而言，顯色指數越高，光源的照明效果會越好，但由于單個LED的光譜分布與傳統光源具有很大不同，因此顯色指數并不能有效的反映實際照明效果，尤其是白光 LED 光源［16］、［17］，而這并不是本文的重點，另外在一些特殊場合，對RGB-LED的顯色指數要求并不高，比如代替汞燈使用的一些場合，因此，這里對樣本輸出的顯色指數并不做過多要求，只要求符合樣本選擇的條件即可。

同時，根據三基色原理，任意色溫的光源可以通過紅綠藍任意比例實現，因此可以根據不同比例的三基色LED搭配來實現不同色溫和顯色指數的LED光源，目前商用RGB-LED色溫主要局限在2000k～6500k。

本文所使用的三基色樣本選取峰值波長分別為627nm、519nm和442nm，在這個條件下，三基色的配比作為輸入量，輸出量為色溫和顯色指數。本文選用參考文獻中的樣本［18］(見表1)，其分布均勻，完全符合RBF神經網絡對樣本的要求。結合RBF網絡性質和聚類思想，其隱含層節點數不會超過學習樣本數。圖2為隱含層節點個數為5時的RBF神經網絡的結構。

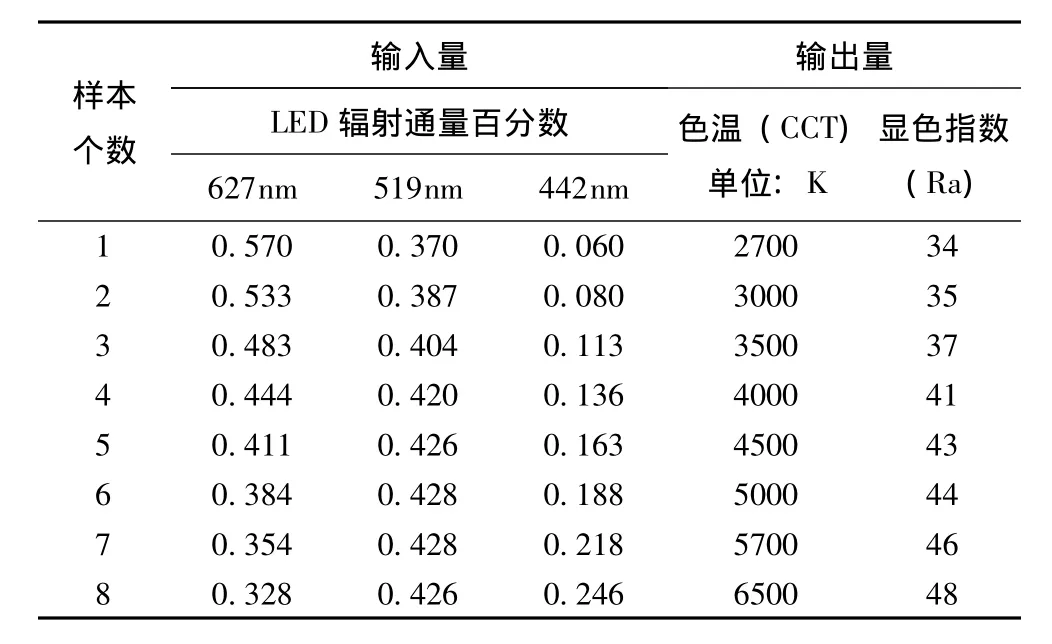
表1 RGB-LED樣本Table 1 RGB-LED samples

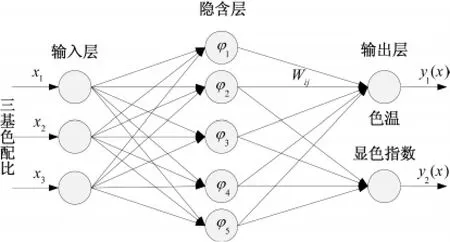
圖2 三基色配比與色溫、顯色指數的RBF網絡結構Fig.2 Three-color ratio and color temperature，color rendering index of RBF neural network structure

為了避免輸入和輸出數據離散程度太大，造成學習數值的溢出和出現網絡預測誤差大，原始數據必須進行預處理，由于輸入是三基色配比數值在0到1之間，因此只需將輸出數據做歸一化處理。

對于輸出色溫來說:

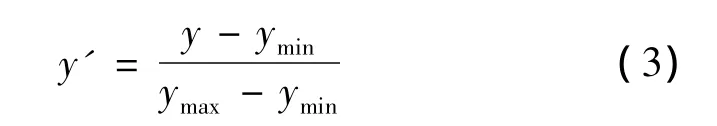
由于對于顯色指數越大，效果就愈好，因此其歸一化采用不同的方式:

3.1 RBF神經網絡的學習和驗證

本文通過樣本的訓練要達到目標關系的擬合，經過三個步驟:

(1)通過網絡學習建立目標關系的網絡模型;

(2)驗證網絡模型在一定誤差范圍下的正確性;

(3)預測在新的輸入情況下，產生理想輸出。

因此，本文隨機將前5個樣本和第8號樣本選作網絡的訓練樣本，用于網絡的訓練構建，剩下的樣本6號作為驗證樣本，7號樣本作為預測樣本來驗證網絡的精度和準確性。網絡的中心數和擴展常數都采用尋優的方式進行確定，而權值的確定將根據隱含層輸出利用最小二乘法求解，其原理是根據式 (5)即輸出層的神經元是隱含層神經元的輸出加權求和，建立矩陣為確保獲得最佳網絡設計。在Matlab中，有專門的MSE(Mean Squared Errors，均方誤差)SSE(Sum of Squares for Error，誤差平方和)性能函數來判斷神經網絡的網絡優越性。MSE數值的大小反映了數據的變化程度，其值越小，越說明該模型具有跟高的精確度用來描述數據關系，具體表達式如下:

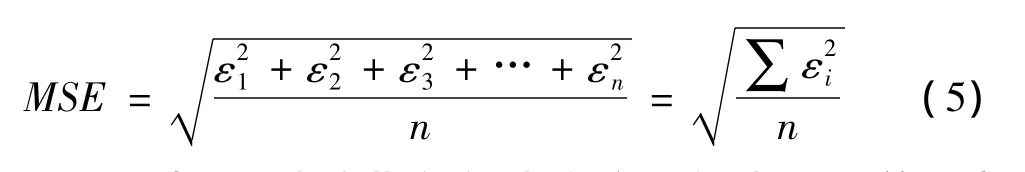
其中，εi代表期望輸出和實際輸出的誤差。本文MSE的數值采用實際輸出反歸一化后的誤差進行計算，因此考慮到數量級的問題，可能會呈現較大的數值。

而SSE則體現了樣本實際輸出值的離散狀況，數值越小，越能反映網絡中心具有標志性，聚類效果優異，產生的預測效果就會更好，因此該網絡就具有很好的泛化能力。在神經網絡學習中，此時的誤差是實際輸出和期望輸出 (歸一化后)的比較而得，考慮到精度的要求，數值上往往呈現接近于零的狀態。

通過兩個性能函數對不同情況下的網絡模型進行判定，以尋優的方式獲得理想網絡模型。

3.2 輸出數據要求

色溫是對光源顏色的度量，人眼對顏色的可辨別顏色的容許色容差一般要求在4～5SDCM內，因此，模擬輸出的色溫偏差必須在一定色容差值內，否則就是無效，而國家標準GB/T24823—2009《普通照明用LED模塊性能要求》其色容差僅要求小于7SCDM即可，由于不同的色溫色容差要求是不同的，結合飛利浦照明公司的數據 (見表2)，本文認為輸出色溫偏差值局限在 (－200，200)作為對結果輸出有效要求。

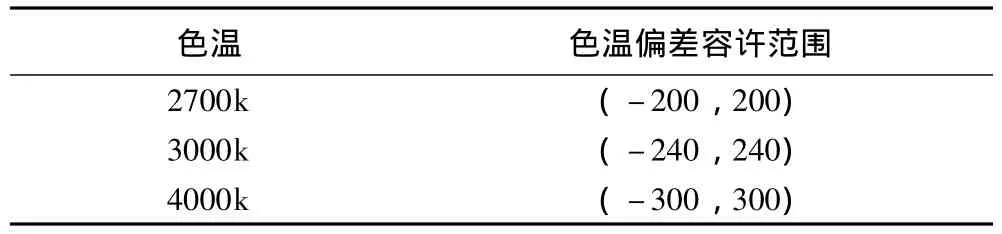
表2 一定色溫允許偏差值范圍Table 2 Deviation range in color temperature

對于顯色指數，該數值是對光源顯色性能的評價，但是，比如指數為1，具體為何種視覺感知，目前并沒有對于顯色指數容許范圍的研究，但根據實際應用中，顯色指數往往精確到整數部分，因此，本文將結合RBF網絡的性能函數進行判定，使得顯色指數的輸出與實際值相差不超過1。

3.3 仿真結果分析

在Matlab上建立基于6個學習樣本的RBF網絡，通過不斷調整隱含層節點數，即中心數，進行，選擇擴展常數從0.2到20，步長為0.2的不同取值，進行優化網絡。

例如，當中心數為5時，見圖3。

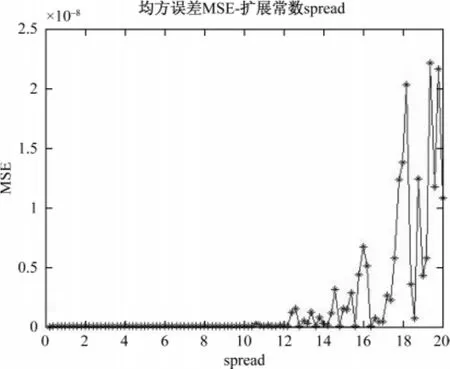
圖3 不同擴展常數下的MSE變化趨勢Fig.3 MSE trends under different extensions constant

由圖3中可知，隨著spread的增加，均方誤差剛開始為零，隨后在擴展常數為12以后發生波動，說明擴展常數并不是越大越好，由圖中可見，此時的MSE在擴展常數0.2到12內都為0，說明此時的網絡可以很好地反映輸入和輸出之間的關系。

由圖4可知，SSE變化趨勢與MSE變化趨勢類似，這說明，網絡精度和泛化能力都有不錯的表現，針對已知樣本具有很好的模擬能力。經Matlab計算，當擴展常數為7.4。

實際上由公式來看，MSE和SSE隨著擴展常數的增加，理論上應該具有相似的趨勢變化，以MSE為標準 (這里的零表示其數量級已經達到10－10或者更小)，通過調整中心數，具體的仿真結果參見表3。

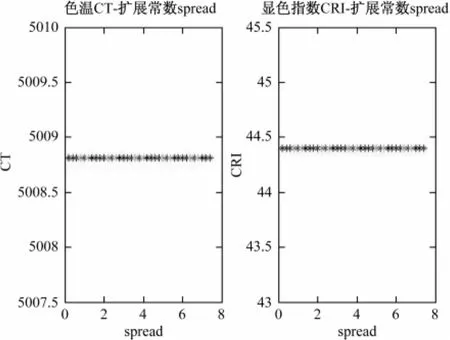
圖4 不同擴展常數下的SSE變化趨勢Fig.4 SSE trends under different extensions constant

表3 網絡模型仿真結果Table 3 The simulation results of the network model

在表3中，顯然隨著中心個數的不斷增加，RBF具有無限逼近的能力，輸入和輸出數據得到很好的模擬。同時從表中可以看出通過聚類方法，中心數為5或者6的網絡模型，在MSE相同時，網絡綜合性能都很優異，不僅輸出誤差適中，而且擴展常數值符合常態，但對于這兩種網絡模型，通常情況下，RBF網絡的設計在精度滿足的情況下，會選取具有最小結構的神經網絡［19］～［20］，以保證神經網絡的泛化能力，因此，本文最終選取第4個網絡模型用于第6號樣本的驗證，見圖5。

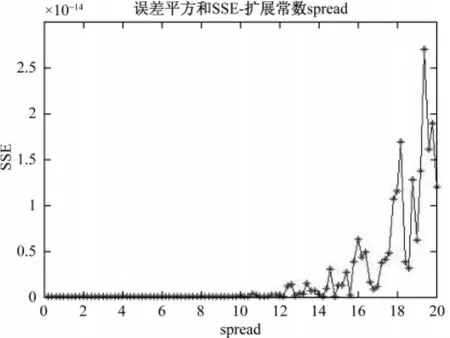
圖5 不同擴展常數時的輸出結果 (反歸一化后)Fig.5 Results under different extensions constant

由圖5可以看出，該網絡模型針對測試樣本6號輸出結果與期望結果始終徘徊在個位數差值，尤其是顯色指數方面，誤差不超過0.5，與實際偏離值都在要求范圍內，顯示該網絡模型的性能優越性，通過網絡運行，此時的MSE在擴展常數為7.4時達到最小，數值為38.9，因此，最后確定擴展常數為7.4，結合7號樣本進行預測，其結果見表4，此時中心個數為5，擴展常數為7.4。

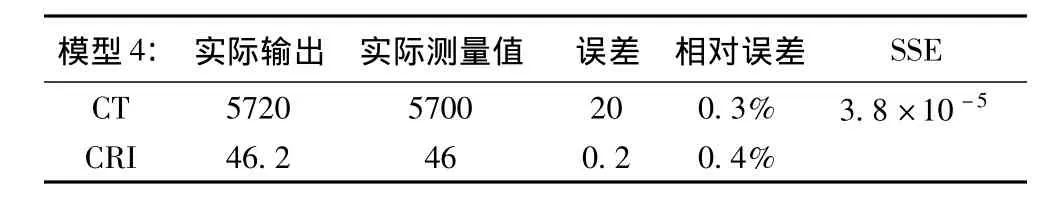
表4 第7號樣本預測結果Table 4 No.7 prediction results

表4結果顯示，該網絡模型預測數據有效，表現在預測色溫和實測數據僅相差20k，優越于飛利浦照明標準對產品色溫的要求，同時顯色指數偏離值只有0.2，相差值不超過1，符合輸出結果要求。輸出結果與測量值相對誤差非常小，色溫和顯色指數的輸出相對誤差幾乎一樣;同時SSE精度很高，表現了該網絡模型的泛化能力仍然具有很高的水平，因此該預測數據完全可以代替測量數據，省去測量步驟。采用該網絡模型可以有效對三基色配比預測色溫和顯色指數，應用于光源的生產和評價。

4 結論

通過RBF神經網絡建立的網絡模型，采用聚類的方法，針對參照樣本進行了學習和仿真，結果顯示，該網絡具有局部逼近的能力，只需三基色比例，就可同時獲得理想的色溫和顯色指數，快捷有效。與傳統的方法相比較，不僅簡單實用，而且功能強大，可同時實現色溫和顯色指數的獲得，對光源生產和及時有效的評價具有重要意義。

［1］Robertson A R． Computation of correlated color temperature and distribution temperature ［J］．J．Opt．Soc．Am．，1968，58(11):1528～1535．

［2］林岳，葉烈武，劉文杰等．二分法優化計算LED光源相關色溫 ［J］．光學學報，2009，29(10):2791～2794．

［3］代彩紅，于家琳，于靖等．顏色溫度和相關色溫的不確定度評定方法 ［J］．光學學報，2005，25(4):547～552．

［4］徐示波，呂毅軍．陳煥庭等．基于二分法的RGB-LEDs配色研究 ［J］．光電技術應用，2009，24(6):7～10．

［5］張浩，徐海松．光源相關色溫算法的比較研究．光學儀器，2006年2月．

［6］譚力，劉玉玲，余飛鴻．光源顯色指數的計算方法研究．光學儀器，2004年8月．

［7］丘行中．光源顯色指數計算的沃爾特方法改進 ［J］．照明，2000，(2):28～321．

［8］殷錄橋，楊衛橋，李抒智，程備，張建華．基于三基色的動態色溫白光發光二極管照明光源．光學學報，2011年5月，第31卷第5期．

［9］彭浩，劉東月，聶叢偉，茹志芹，黃杰．白光LED的顯色指數模型研究．第十二屆全國LED產業研討與學術會議論文集，2010年．

［10］Buhmann M D． Radial Basis Functions:Theory and Implementations［M］．Cambridge Univ．Press，2003:56～104．

［11］張雅，向虎，郭芳瑞．RBF網絡模型參考自適應控制在溫度控制中的仿真研究 ［J］．系統仿真學報，2008，28(2):429～432．

［12］陳琪．基于RBF的語音情感識別方法的研究．碩士論文，長沙理工大學，2010年3月．

［13］李彬．徑向基函數神經網絡的學習算法研究．碩士論文，2005年4月，山東大學．

［14］劉文菊，郭景．RBF神經網絡中心選取OLS算法的研究 ［J］．天津工業大學學報，2002，21(2):71～73．

［15］王紅萍，金彥豐，曹海軍，陳曉輝．基于徑向基函數網絡的水聲信號預測模型研究．艦船電子工程，2008年第10期．

［16］CIE Technical Report 177:2007．Color rendering of white LED light sources．ISBN 9783901906572．

［17］Wendy Davis，Yoshi Ohno．Towards an improved color rendering metric．Proc．of SPIE Vol．5941 59411G．

［18］Artūrasukauskas， Rimantas Vaicekauskas， Michael Shur．Solid-state lamps with optimized color saturation ability，OPTICSEXPRESS，2010，Vol．18，No．3．

［19］Niyogo P， Gorisi F． On the Relationship between Generalization Error，Hypothesis Complexity and Sample Complexity for Radial BasisFunction ［J］． Neural Computation，1996(8):819～842．

［20］Moody J．The Effective Number of Parameters:A Analysis of Generalization and Regularization in Nonlinear Learning System ［J］．NIPS4，1992:847～854．