無線傳感網OFDM 系統中信道估計與均衡技術的算法設計*

郭旻軒，瞿 曉，奚錦程，王 軍，張 萌

(東南大學電子科學與工程學院，南京 210096)

正交頻分復用OFDM(Orthogonal Frequency Division Multiplexing)是一種高效多載波調制技術，能有效降低多徑干擾和信道頻率選擇性衰落的影響［1］，被認為是4G 無線系統的核心技術之一。目前已應用于數據音頻廣播、高清晰度數據電視、無線城域網等系統［2－4］。信道估計與均衡是OFDM 系統中關鍵技術，現有的信道估計與均衡算法如最小二乘法(LS)、最小均方誤差法(MMSE)等在精確度或復雜度上不盡如人意。無線傳感器網絡(WSN)的OFDM 系統中，信道估計可采用基于輔助導頻的信道估計方式實現［5］。

1 OFDM 系統

1.1 OFDM 系統簡介

OFDM 系統模型如圖1所示。在發射端，發送的數據經信道編碼，映射，串并轉換送入插入導頻和虛擬子載波單元，再經過IFFT 完成OFDM 系統的調制操作，添加循環前綴作為保護間隔，通過并串轉換將數據送入中頻調制的IF 信號;在接收端，經過信道后的數據，進行同步操作，串并轉換，去掉循環前綴后送入FFT 完成OFDM 系統的解調操作，對進入頻域的數據做信道估計，得到當前實時的信道響應，通過均衡處理以消除信道的影響;隨后，再經過解映射和譯碼最終得到接收的傳輸碼流［6］。其中信道估計與均衡直接影響系統性能。

1.2 信道估計與均衡

設在插入循環前綴前的時間序列為xi，k，變換到頻域為在經過信道后為Xi，k，則接收端接受到的信號為Yi，k，則有:

其中，Hi，k是信道對第i個OFDM 符號第k個子載波位置的頻率響應，Wi，k是信道對第i個OFDM 符號第k個子載波產生的噪聲。

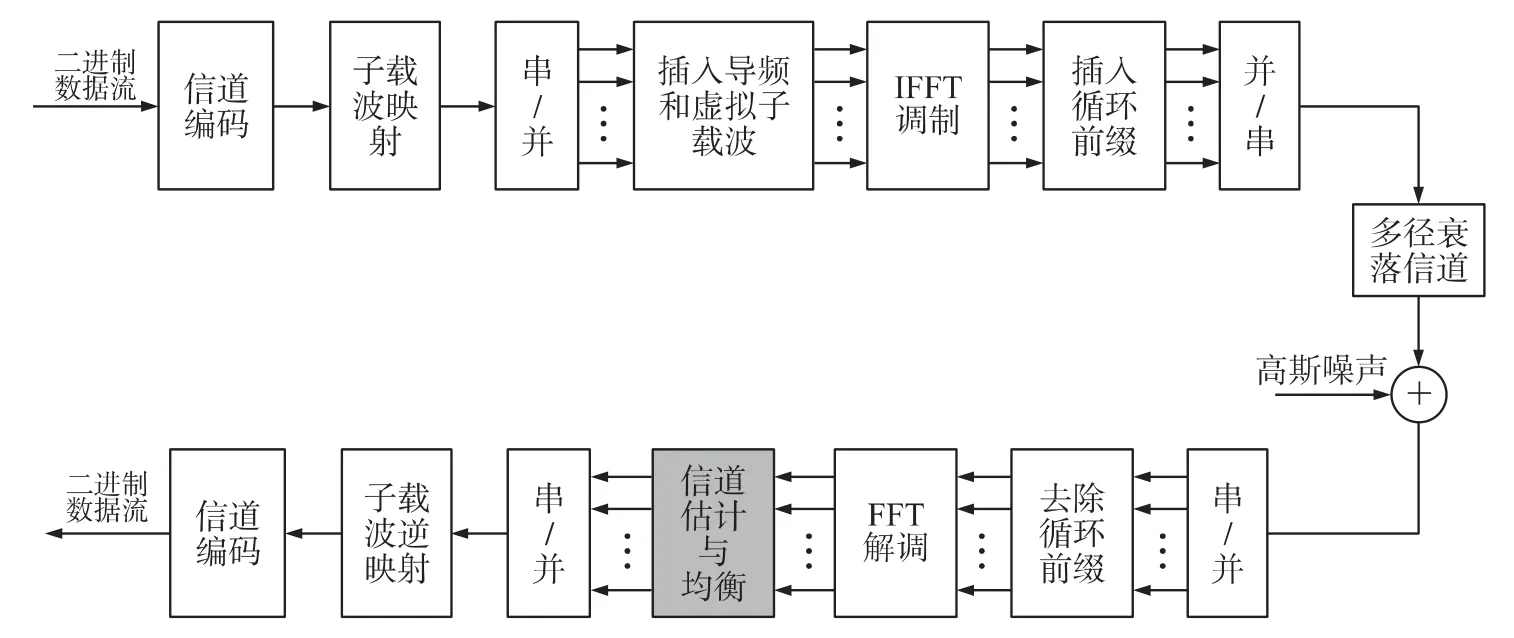
圖1 OFDM 系統結構

信道估計的目的在于通過有限的已知數據點估算出整個信道特性Hi，k的估計值～Hi，k，而信道均衡的目的在于通過信道估計得到的～Hi，k，根據接收機接收到的Yi，k計算出原始的發送數據Xi，k。

導頻輔助的信道估計常用兩種導頻圖案［7］:塊狀導頻和梳狀導頻(如圖2)。塊狀導頻在若干時間點上的所有頻率插入導頻，能夠適應緩慢衰減的信道。而梳狀導頻是在所有時間點的若干頻率上插入導頻，可以適應快速變化的信道，本文選用梳狀導頻方式。

圖2 導頻圖案

2 算法

2.1 經典信道估計算法

經典算法主要有最小二乘法(LS)［8］和最小均方誤差法(MMSE)［9］。規定:發送端調制后發出的數據用X 向量表示(頻域);接收端接收到的解調前的數據用Y 向量表示(頻域);信道頻響用H 向量表示;下標p 表示導頻;導頻個數為Np。列向量Hp表示導頻信息經過信道的頻響:

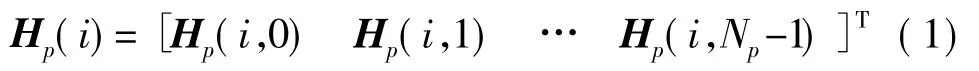
Hp(i，k)表示信道對第i個OFDM 符號中的第k個導頻的頻域響應。

根據LS 算法，信道估計為:

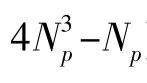
同時，在用LMMSE 進行估計時，自相關矩陣RHpHp和信噪比SNR 的值需要事先設定。這種依賴于經驗值的做法非常不利于算法的硬件映射。并且，如果信道改變或者估計錯誤，會對系統的精確性造成破壞性的影響。

2.2 改進的LMMSE 信道估計算法

針對LMMSE 依賴于經驗值的問題，論文“A Study of Channel Estimation for OFDM Systems Capacity for OFDM System and System Capacity for MIMO-OFDM Systems”改進的LMMSE 算法中選擇最大的抽頭系數MST(The Most Significant Taps)［11］，根據主要路徑的特征進行估計RHpHp和SNR，然后計算導頻點信道LMMSE 估計值。估計方法如下:

首先計算出時域中的導頻響應:

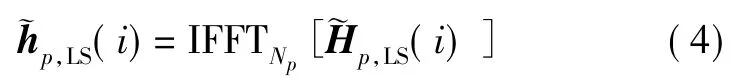
計算得到每個導頻附近NMST個OFDM 符號的平均能量:

并選出L′個使PLS(k)最大的k，將這些k值組成的集合記為Ω。保留這些導頻值，將其余導頻的沖擊響應(時域)置零。于是可以得到:

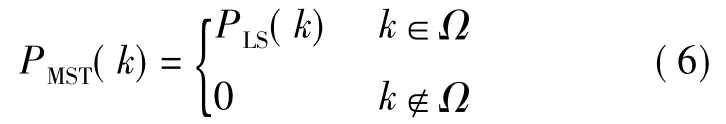
可以證明，估計的自相關矩陣～RHpHp是一個循環矩陣，矩陣的第一行～A 可以這樣得到［12］:

其中估計的信噪比為:

最后得到估計的信道頻域響應:

2.3 信道估計與均衡的快速算法

上述的信道估計算法雖然解決了LMMSE 估計中依賴經驗值的問題，并且利用循環矩陣降低運算量，但是計算復雜度仍較高。必須注意到的是，上述算法涉及2 次IFFT/FFT 運算，若加上插值，就有3次IFFT/FFT 運算。這種運算非常消耗硬件資源，在做算法的硬件映射時，會大大提升硬件成本并且降低系統的運行速度。

為此，本節設計了以下快速算法(Fast LMMSE)。

注意到式(11)中是循環矩陣與～Hp，LS的相乘，這樣的運算可以用循環卷積來代替:

由DFT 運算的共軛對稱性及IFFT 與FFT 關聯性可以進行如下變換:

用(·)*表示共軛矩陣，?表循環卷積。

由循環卷積特性DFT［f1(k)?f2(k)］=DFT［f1(k)］DFT［f2(k)］與二重FFT 運算式FFT{FFT［f(k)］}=Nf((N－k)modN)，k=0，1…(N－1)可得:

經過這樣的化簡后不難發現，以移位與向量乘法取代復雜的矩陣乘法化簡了運算。此外，結合下文的補零DFT 插值算法，還可以減少兩次IFFT 的運算量。

2.4 插值算法

因為導頻是呈梳狀均勻插入在有效數據中傳輸的，故得到信道估計矩陣～Hp，LMMSE后，只需對有效數據所在點進行插值便可以得到有效數據對應的信道頻域響應。

DFT 插值算法依據時域補零操作等效于頻域插值的原理［13］，可以發現FFT和IFFT 運算在之前的運算中包括在整個OFDM 系統中被反復的應用。所以盡管可以進行插值的算法很多，考慮到插值算法對前面算法的承接關系，這里選用基于補零DFT插值。導頻點數量為Np(偶數)，相鄰導頻點間數據點數為Nd，插值過程分3 步進行，具體如下:

(3)插值得數據點信道頻響估計值:

其中Ndp=Np(1+Nd)。對應抽取～H(i)向量中數據點頻響估計值便可進行信道均衡。

不難發現，結合插值算法后，算法進一優化，比上文改進的LMMSE 算法節省了兩次IFFT 運算，僅需一次NpIFFT，一次NdpFFT和一次Np位向量乘法，共(Np/2)lb(Np)+(Ndp/2)lb(Ndp)+3Np+2 次乘除運算和少量加減運算，整個算法復雜度更低，更易于硬件實現。但需注意，此算法適用于導頻點等間距的、邊緣點均為導頻的情形，并非所有的導頻圖案都適用，因此在具體的導頻設計時應該加以注意。

3 OFDM 系統參數與MATLAB 仿真分析

3.1 OFDM 導頻結構與算法步驟

結合本文所提出的快速算法，確立OFDM 符號導頻結構如圖3所示。

圖3 OFDM 符號導頻結構

在用于發送有用數據的子載波為48個時，最少的IFFT點數為64。為便于后續IFFT 估計和插值計算，每隔7個數據點插入一個到頻點。剩余8個不傳輸數據的虛擬子載波。將這些虛擬子載波分布在直流信道和頻譜中央。這樣可以消除信號直流成分，節省功率，同時能夠降低信號的峰均比0，降低對器件的性能要求。所以56個非零信道映射到64點輸入的IFFT 當中采用圖4所示指定方式。

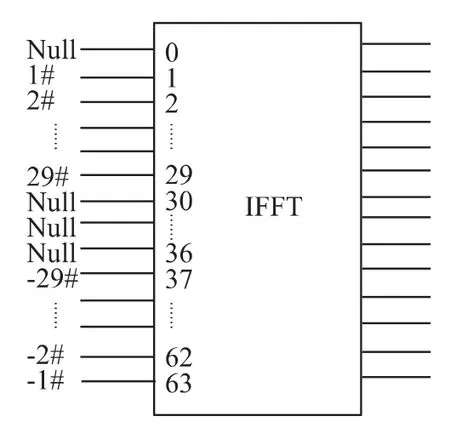
圖4 IFFT 輸入方式

這種導頻結構將使信道估計與均衡算法復雜度更低，更易于電路實現。

3.2 Matlab 仿真

按3.1 節導頻結構與上文算法，進行信道估計與均衡的Matlab 仿真以驗證其性能。針對無線傳感網的特征，仿真信道采用帶多普勒頻移的6 徑瑞利衰落信道，選取參數如表1所示。

我們對文中提及的四種算法進行了Matlab 仿真:分別用四種算法對經過相同信道的相同數據進行信道估計與均衡，并將均衡后的數據與原數據比較，得到的誤碼率作為衡量算法精確度的標準。為保證仿真結果的可信度并表征算法的效果，我們增加了不經過估計與均衡的數據作為參考組。

仿真結果如圖5所示。由圖5 可以看出，經驗值偏差對LMMSE 算法誤碼率產生的破壞性影響——它的精確度比LS 算法還要差。而經過改進后的簡化算法(Simplified LMMSE)的誤碼率則明顯降低，在信噪比16 dB 時誤碼率為0.000 2，僅為16 dB 時LS 算法誤碼率的8.7%。從圖中還可以看出，基于改進算法的快速算法(Fast LMMSE)與改進算法的精確度一樣，說明我們對算法的改進是無損于其精確度的。

圖5 Matlab 仿真結果:誤碼率－信噪比圖線

表1 Matlab 仿真參數選擇

除精確度意外，我們的另一個關注點，算法復雜度可以通過計算加以比較。在算法的FPGA 實現時，復雜度主要取決于乘除運算，故可用乘除運算次數衡量。各種算法復雜度比較如表2。

由表2，在本文所采用的OFDM 系統64點FFT，8點導頻構架時，基于本文改進算法的快速算法復雜度比LS 算法提高8.49%，比LMMSE 降低73.98%，算法復雜度有大幅度降低。同時，算法所達到的誤碼率表明，結合適當的編碼技術以及幀結構后，完全可以滿足目前通信系統要求的精確度。

以上結果說明，本文提出的快速算法，在保證信道估計較高性能的同時，降低了運算復雜度，這更利于高性能OFDM 信道估計與均衡器的FPGA 硬件實現。

表2 本文所述幾種算法復雜度的比較

4 結束語

本文在分析WSN 的OFDM 系統基于導頻輔助信道估計與均衡算法的基礎上，改進了LMMSE 算法，并結合DFT 插值算法，設計了一種既有較高精確度又具有較低復雜度的快速算法，避免了復雜的矩陣運算和多余的FFT 運算。確立OFDM 系統64點FFT，8點梳狀導頻構架，用Matlab 進行系統仿真驗證了算法的準確性。進一步的工作將放在信道估計與均衡的FPGA 硬件實現上。

［1］Weinstein S B，Ebert P M.Data Transmission by Frequency-Division Multiplexing Using the Discrete Fourier Transform［J］.IEEE Trans Common，1971，19:628－634.

［2］ETSI，European Telecommunications Standards，Radio Broadcasting Systems.Digital Audio Broadcastingto Mobile，Portable and Fixed Receivers［S］.2nd ed.EN 401 v1.4.1 1997a:493－497.

［3］ETSI，European Telecommunications Standards，Digital Video Broadcasting.Framing Structure，Channel Coding ＆ Modulation for Digital Terrestrial Television［S］.EN 421 v1.1.2，1997b:300－421.

［4］lEEE.IEEE Standard for Local and Metropolitan Area Networks Part 16:Air Interface for Fixed and Mobile Broadband Wireless Access Systems Amendment 2:Physical and Medium Access Control Layers for Combined Fixed and Mobile Operation in Licensed Bands and Corrigendum 1［S］.IEEE Std 802.16e－2005，2006.

［5］張繼東，鄭寶玉.基于導頻的OFDM 信道估計及其研究進展［J］.通信學報，2003，24(11):116－124.

［6］史治國，洪少華，陳抗生.基于XILINX FPGA 的OFDM 通信系統基帶設計［M］.杭州:浙江大學出版社2009:1－11.

［7］趙冬，閆發軍，王文博.OFDM 系統中導頻設置方式對信道估計算法性能的影響［J］.中國無線電，2006，5:57－61.

［8］Jeon W G，Pail K H，Cho Y S，An Efficient Chanel Estimation Technique for OFDM Systems with Transmitter Diversity［J］.Indoor and Mobile Radio Communication，London，UK，2000，9:1246－1250.

［9］Morelli M，Mengali U.A Comparison of Pilot Aided Channel Estimation Methods for OFDM Systems［J］.IEEE Trans Signal Processing，2001，49(12):3065－3073.

［10］Edfors O，Sandell M，van de Beek J J，et al.OFDM Channel Estimation by Singular Value Decomposition［J］.Communications，IEEE Transactions on，1998，46(7):931－939.

［11］Zhou Wen.A Study of Channel Estimation for OFDM Systems Capacity for OFDM System and System Capacity for MIMO-OFDM Systems［D］.Hongkong:University of Hongkong，2010:65－68.

［12］Minn H，Bhargava V K.An Investigation into Time-Domain Approach for OFDM Channel Estimation［J］.Broadcasting，IEEE Transactions on，2000，46(4):240－248.

［13］胡廣書.數字信號處理理論、算法和實現［M］.北京:清華大學出版社，2009:137－138.

［14］胡樂.多載波系統降低峰均比技術的研究［D］.南昌:南昌大學，2007:30－30.