四象限非對稱風場對風暴潮的改進研究

傅賜福，于福江，2，劉秋興，李濤

（1.國家海洋環境預報中心，北京 100081；2.國家海洋局海洋災害預報技術研究重點實驗室，北京 100081）

臺風風暴潮是我國頻發的重大海洋災害，其造成的經濟損失從20世紀90年代后已有明顯增加的趨勢，風暴潮的預報及研究是海洋防災減災的重要研究課題。經過國內外眾多學者幾十年的研究揭示了風暴潮發生的主要機制和一般規律，總的而言，風暴潮是氣象因素占主導、多種海洋要素綜合作用的結果，包括風、氣壓、天文潮、近岸海浪、河口徑流等，風暴潮與海洋各要素的耦合作用在近海尤為復雜。

風場作為引發風暴潮的主要因子，對風暴潮預報和研究起到關鍵作用。到目前為止，人們只能利用有限的手段去研究臺風風壓場，歸納起來，主要有三大類：第一類是圓對稱風場模型（高橋，1939；藤田，1952；Jelesnianski，1965；Holland，1980）；第二類為改進的非對稱風場模型，如非對稱結構風場模型（章家彬等，1986），橢圓形對稱的風壓模型（陳孔沫，1994），特征等壓線風場模型（朱首賢等，2003）；第三類為氣象數值預報模型，如MM5，WRF。這三類風場模型對臺風風壓場的刻畫各有優劣：第一類模型便于描述計算，但未能客觀反映不同類型臺風的風壓場結構特征；第二類模型則要考慮天氣形勢、時空變化，較難去定其經驗參數；氣象數值預報模式對初始場資料要求較高，且空間分辨率較低，臺風路徑和強度預報也有待進一步提高。

隨著風暴潮預報往精細化發展，更準確風場的獲得成為了一個重要研究方向，本文將引入一個基于Holland模型風場改進的四象限非對稱模型風場，并參考美國NOAA熱帶氣旋實時產品提供的7級、10級、12級風圈資料，利用ADCIRC模型建立的高分辨率風暴潮模式對1117號熱帶氣旋“納沙”引起的強風暴潮進行數值模擬，對比四象限風場和Holland風場對風暴潮改進效果并分析結果。

1 四象限模型風場

1.1 Holland模型風場

Holland模型風場是較常用的臺風模型風場（Holland et al，1980），臺風氣壓場分布見公式（1）：

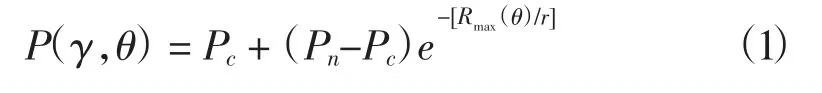
其中，P（γ，θ）是距臺風中心γ處的海表面氣壓值，為徑向距離γ、方位角θ的函數；Pc為臺風中心氣壓，Pn為臺風以外不受干擾的背景氣壓，取為1 012百帕；Rmax是臺風最大風速半徑，為方位θ角的函數。

在Holland臺風風場的計算中，假設梯度風平衡，即氣壓梯度力、離心力與科氏力的平衡所得到切向風速，見公式（2）。

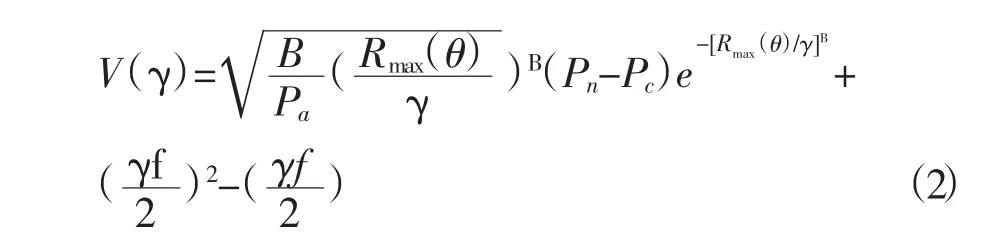
其中，V（γ）為距離臺風中心的切向風速，ρa為空氣密度，f為科氏參數；B是臺風輪廓參數，表征臺風眼區直徑和切向速度梯度，一般取值1.0～2.5。該模型計算得到的風場是軸對稱的，在臺風移動方向的右半圓科氏力作用使得切向風速加強，左半圓切向風速減弱。

1.2 四象限非對稱風場模型

而實際上，大部分的熱帶氣旋風場結構是非對稱的，這樣的熱帶氣旋在靠近或者登陸時會對風暴潮預報帶來較大誤差。而如果能將所觀測較精確的風場資料分為四個象限使我們構造出來的風場更接近觀測，就能進一步減少預報誤差。Xie等（2006）提出了四象限非對稱風場模型，具體的風場構造及計算如下：

假設已知1117號強臺風“納沙”實況見表1。為了易于求解，將Rmax寫成方位角θ的多項式函數，見公式（3）。

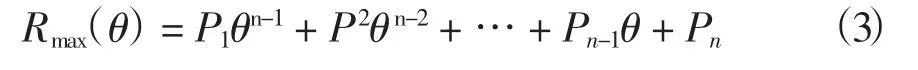
對于公式（2）中，已知實況點的信息，在Vmax=V(γ=Rmax)的情況下（Vmax是最大風速），可得：

對于某個象限的風力（例如7級）的風圈半徑是已知的，利用公式（2）即可求解得到Rmax。通過每個象限算出的Rmax（共4個）代入公式（3）中，其中n=5，通過多項式擬合即可求解出P1、P2、P3、P4、P5，這樣就可以求得距離臺風中心任意位置點的風速。由于每個象限某個風力風圈半徑不盡相同，因此所計算的風場分布是非對稱的。

表1 1117號熱帶氣旋“納沙”某一時刻的風場特征信息

2 風暴潮模式及數據來源

2.1 ADCIRC風暴潮模式

ADCIRC模式是基于有限元方法的跨尺度（大洋、近岸、河口）水動力計算模型，采用非結構三角形網格（Westerink et al，2006）。通過基于垂直平均的原始連續方程和運動方程來求解自由表面起伏、二維流速等3個變量，在球坐標系下，連續方程和運動方程可表示為：初始條件為：ζ=u=v=0；海岸邊界條件為：邊界的法向速度為0；

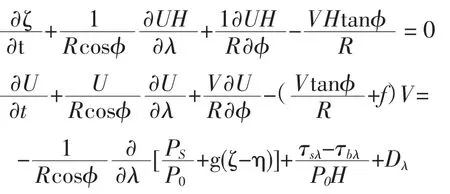
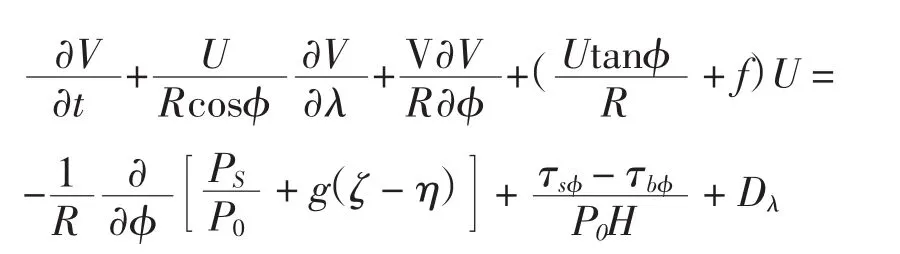
開邊界條件：靜壓邊界；

模式中求解所需物理變量的過程中，空間采用有限元法離散，時間采用有限差分法。將連續方程和運動方程通過引入空間變量數值加權參數進行結合求解，提高了計算結果的穩定性，時間步長取為20 s；

底摩擦力與深度平均流呈二次平方律關系，底摩擦系數采用線性與二次律混合形式；海面風應力與風速呈二次平方律關系，風拖曳系數采用Garratt公式，Cd=0.001×（0.75+0.667）×W，（2‰≤Cd≤3‰）。

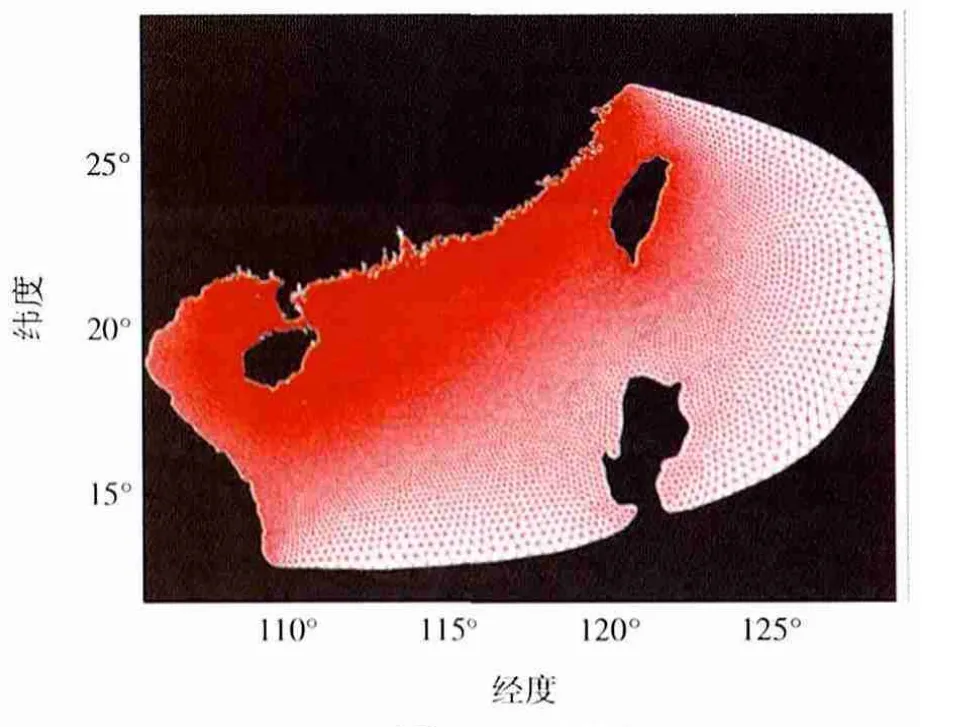
圖1 計算區域網格劃分

模型的計算區域及網格分布見圖1所示，計算區域包括了東海南部和大部分南海，開邊界網格分辨率為20～30 km，除粵西的近海網格分辨率為1～4 km，粵西近海網格分辨率為0.4～0.8 km，整個計算區域包括121 880個計算格點，236 554個計算單元。

2.2 臺風數據來源

文中四象限臺風資料采用美國國家颶風中心（NHC）的熱帶氣旋最佳路徑資料，該資料同化了被動微波傳感器資料（Special Sensor Microwave Imager，簡稱SSM/I）、快速遙感主動散射計數據（Quick Scatterometer，簡稱SCAT）、微波探測風場數據（Advanced Microwave Sounding Unit，簡稱AMSU）等海面觀測風場資料（Mueller et al，2006）。目前，NHC所提供的熱帶氣旋最佳路徑資料（包含四象限風圈半徑預報信息）已被美國海洋與大氣管理局（NOAA）業務化使用。

文中的另一個風場Holland模型的資料也是取自NHC的熱帶氣旋最佳路徑資料。這樣可以客觀地比較兩種不同模型風場對風暴潮的影響。

3 1117“納沙”風暴潮模擬分析

3.1 1117“納沙”概況

2011第17號強臺風“納沙”（NESAT）于2011年9月24日上午在西北太平洋洋面上生成，9月26日夜間和29日7時兩度加強成為強臺風，并以強臺風的強度于29日14時30分前后在海南文昌市登陸，29日21時前后在廣東徐聞再次登陸，是2011年登陸我國強度最強的臺風。受其影響，9月28日至30日，從廣東省、海南省、廣西省沿海先后出現了一次強風暴潮過程，廣東三灶、閘坡、湛江、南渡、海南秀英潮位站均出現了超過當地警戒潮位的高潮位，以上三省直接經濟損失超過30億元。圖2為9月29日-30日上午的臺風路徑、驗潮站和浮標分布及關心區域水深分布。

3.2 風暴潮模擬

利用已建立的風暴潮模式，分別用原Holland模型風場和四象限非對稱模型風場驅動計算風暴潮進行對比分析。

圖3和圖4分別為珠海、臺山、海安、秀英、水東、硇洲、湛江、南渡等8個潮位站模擬與實測的對比圖，表1為各站模擬最大風暴增水與實測的對比及誤差。從圖和表中可以看出，位于雷州半島東岸的水東、硇洲、湛江、南渡潮位站在兩種風場的驅動下模擬風暴潮曲線、最大風暴增水數值均相差不大，與實測值接近；而位于珠江口東岸和瓊州海峽的潮位站在四象限風場的驅動下模擬效果明顯優于原Holland風場驅動，更接近實測值，原Holland風場驅動的最大風暴增水平均相對誤差為23.3%，而四象限風場驅動的最大風暴增水平均相對誤差僅為5.4%。

3.3 風暴潮模擬差異分析

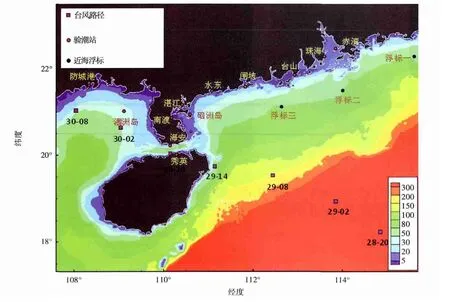
圖2 關心區域水深、“納沙”路徑（紫）及所涉及驗潮站、浮標（紅）示意

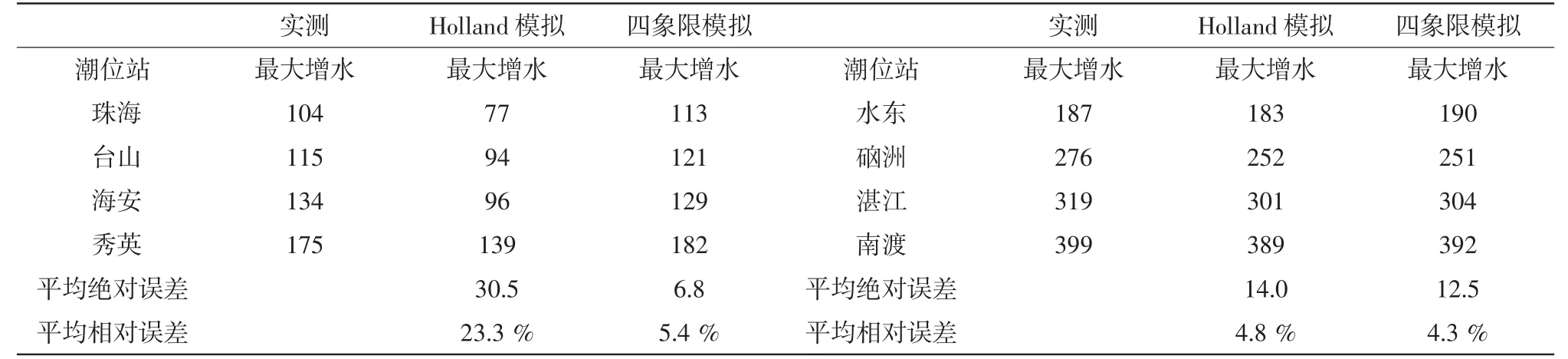
表2 各站最大風暴增水模擬與實測對比（單位：cm）

“納沙”是較典型的西北路徑影響粵西的熱帶氣旋，在500 hpa高空圖天氣形勢是副高穩定地位于熱帶氣旋的北側，反映在地面天氣圖上是熱帶氣旋的北側為高壓控制，因此此路徑下熱帶氣旋東北和西北象限的風力及風圈往往要比東南和西南大。

為了考察風暴潮差異的原因，本文選取了廣東近海3個浮標的風資料進行對比，這3個浮標均位于“納沙”路徑的北側（詳見圖2），圖5為其在兩個風場模型輸出風速、風向與實測的對比。從圖中可以看出，通過同化更多風場資料的四象限風場參數所構造的風場在“納沙”路徑的北側得到了加強，無論風速還是風向均比Holland模型構造得到的風場更加接近實測值。

此外，為了全面考察兩種風場模型構造風場對風暴潮的差異，本文選取了最大風暴增水出現時段、即恰好也是臺風登陸前和登陸后陸后的兩個時次（29日14時和29日18時），考察上述兩種風場模型構造的臺風風場差異及對風暴潮引起的差異。

圖6為29日14時和29日18時兩個時次兩種模型構造的風場、風暴潮差值（四象限-Holland）。從圖6a、圖6b和圖6c、圖6d來看，四象限模型所構造的風場在西北和東北象限的風圈明顯大于Holland模型且呈現出明顯的非對稱性，即西北和東北象限比西南和東南象限的風力和風圈明顯要大。從圖6e和圖6f來看（四象限-Holland的風暴潮差值，在這段落簡稱“風暴潮差值”），在“納沙”登陸前（29日14時），在珠江口到珠江口以西、海南省東北部沿海風暴潮差值為0.2～0.4 m；在“納沙”登陸后（29日18時），在珠江口到珠江口以西沿海的風暴潮差值減小為0.1～0.3 m，在瓊州海峽附近沿海的風暴潮差值增加為0.3～0.5 m；而在粵西到雷州半島東岸沿海的風暴潮差值幾乎為0。這些變化反應在潮位站的時間序列上正如圖3和圖4所示。

圖4 水東（a）、硇洲（b）、湛江（c）、南渡（d）潮位站風暴潮模擬值與實測值比較（原Holland風場-黑色，四象限風場-藍色，實測-紅色）

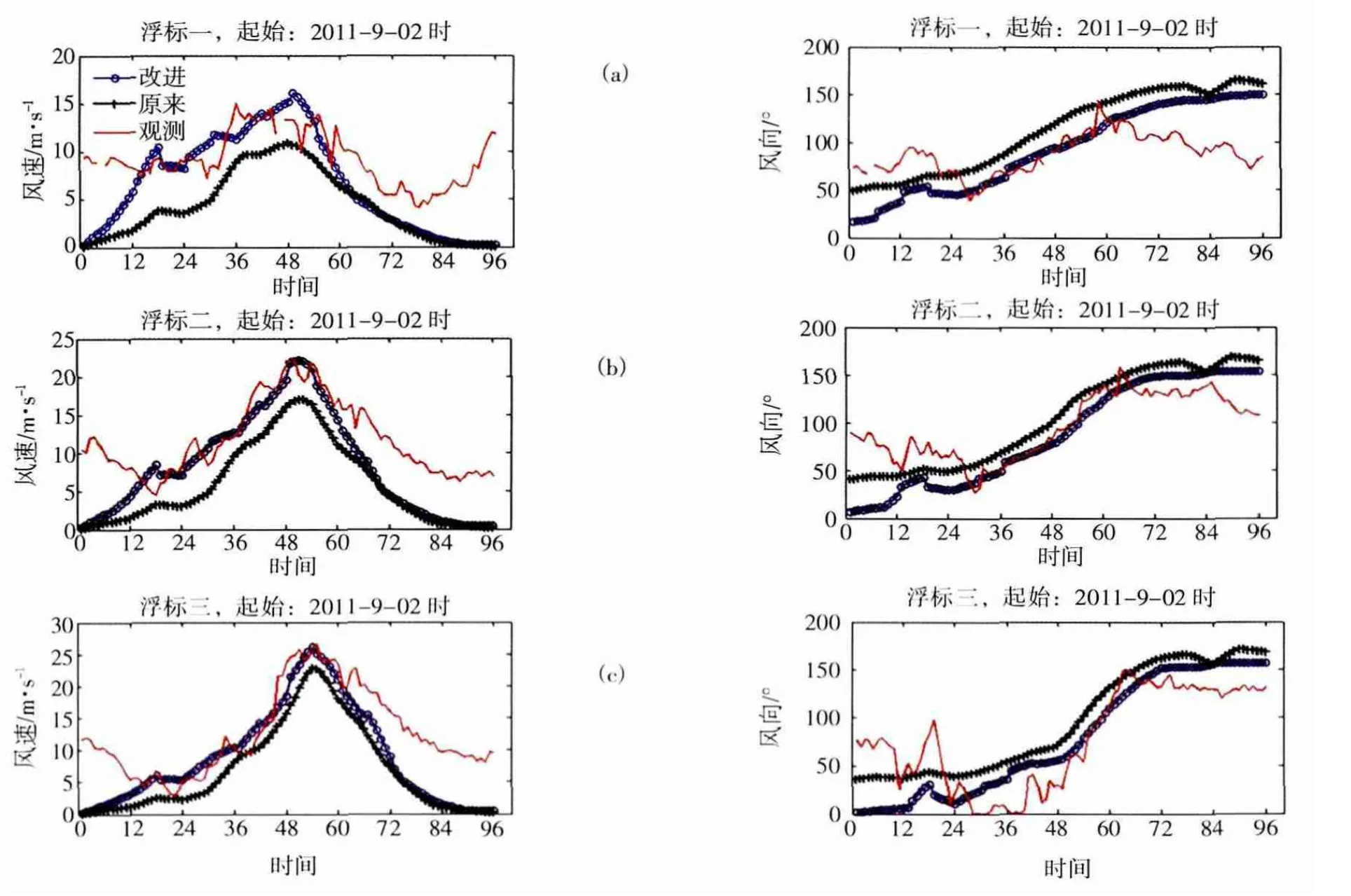
圖5 近海浮標一（a）、浮標二（b）、浮標三（c）的風速風向兩個模型計算值與實測值比較（原Holland風場-黑色，四象限風場-藍色，實測-紅色）

究其原因：Holland模型在臺風實況已知的情況下只能通過改變來調整風圈大小，容易造成熱帶氣旋各象限風場的顧此失彼，而四象限模型可調整風場參數較多，因而四象限模型能夠比Holland模型更好地刻畫“納沙”臺風風場的非對稱性。

4 結論

（1）本文介紹了Holland模型風場和四象限非對稱模型風場的求解思路，并分析了兩者所構造風場的差異和適用性。

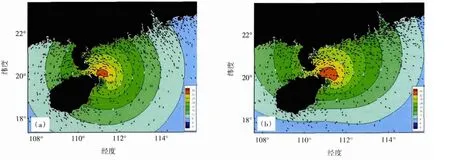
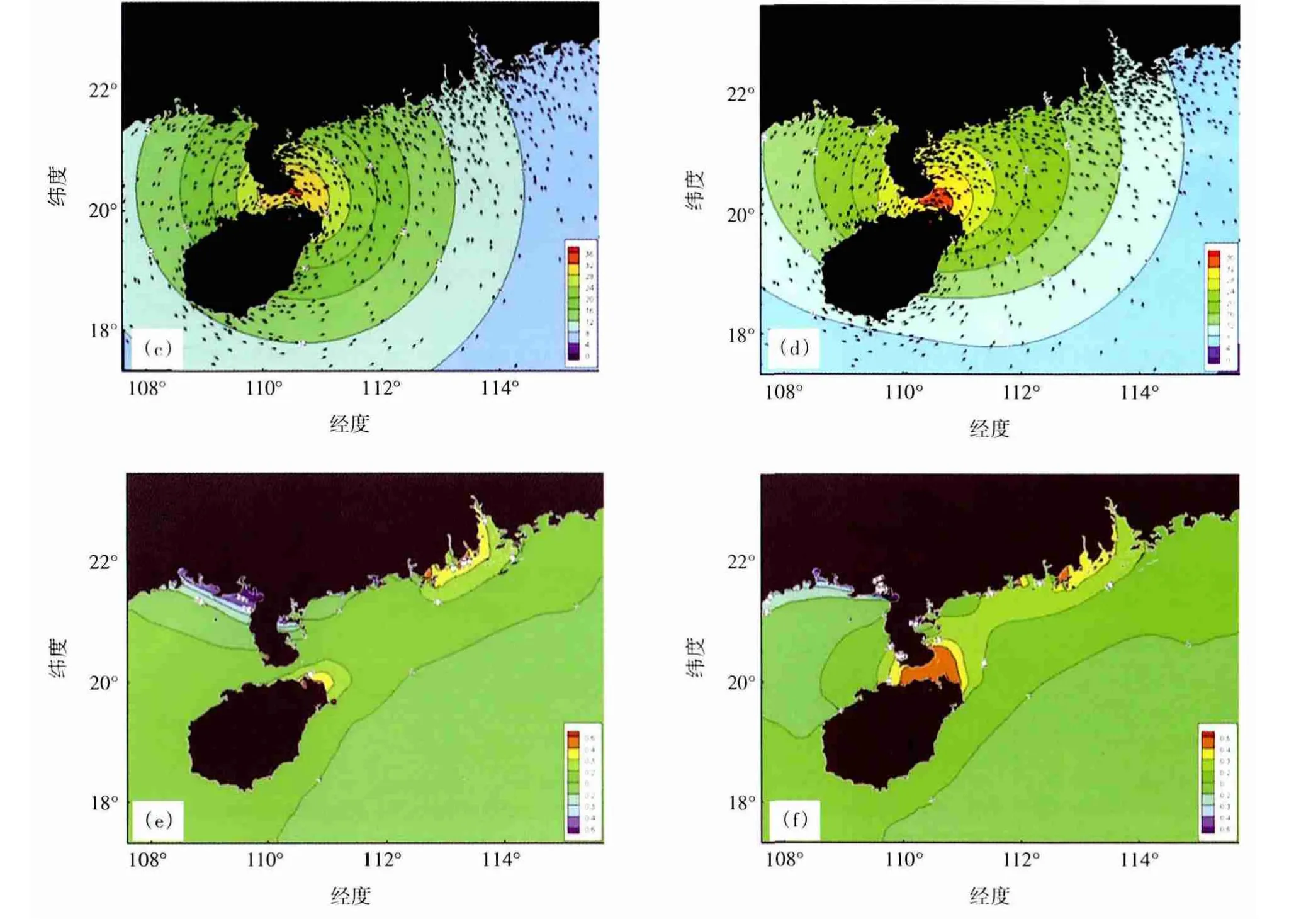
圖6 29日14時和29日18時兩種模型構造的風場、風暴潮差值

（2）利用ADCIRC模型建立了適合華南沿海的高分辨率風暴潮模式，將上述兩種模型風場作為強迫場模擬1117號強臺風“納沙”風暴潮過程，證明該模型是可信的。

（3）通過風暴潮模擬結果可知：在雷州半島東岸沿海潮位站模擬最大增水平均相對誤差基本一致的情況下，珠江口到粵西沿海、瓊州海峽附近沿海潮位站模擬最大增水平均相對誤差由23.3%降低到5.4%，能夠全面地刻畫整個受影響岸段的風暴潮發生發展情況。究其原因：四象限模型相比Holland模型更靈活、能夠更好刻畫“納沙”臺風非對稱風場。

Holland G J，1980.An analytic model of the wind and pressure profiles in hurricanes.Mon Wea Rev，108：1212-1218.

Mueller K J， DeMaria M， Knaff J， 2006.Objective Estimation of Tropical Cyclone Wind Structure from Infrared Satellite Data.Weather And Forecasting，21：990-1005.

Westerink，Joannes J，Coauthors，2008：A basin to channel scale unstructured grid hurricane storm surge model applied to Southern Louisiana.Mon Wea Rev，136：833-863.

Xie L，Bao S W，Leonard J，2006.A real-time hurricane surface wind forecasting model： formulation and verification.Mon Wea Rev，134，1355-1370.

陳孔沫，1994.一種計算臺風風場的方法，熱帶海洋，13（2）：41-48.

朱首賢，沙文鈺，丁平興，等，2002.近岸非對稱臺風場模型.華東師范大學學報（自然科學版），3：66-71.