雙驅動六點支承平臺設計及調平算法*
王大志,謝占功,何 凱,杜如虛
(1.廣州中國科學院先進技術研究所 精密工程研究中心,廣東 廣州 511458;2.中國科學院深圳先進技術研究院 精密工程研究中心,廣東 深圳 518055)
引 言
調平是精密儀器及機械領域常見的一類問題。如經緯儀、陀螺羅盤以及雷達等儀器設備的工作都需要一個水平基準[1-3]。調平對充分發揮這些儀器設備的精度和工作能力,提高其機動性具有重要意義。因此,作為軍事及民用等領域廣泛應用的一項基礎技術,平臺調平受到國內外相關研究人員的普遍關注。
三點支承是精密機械設計中的一個重要概念,它是指不共線的三點可以確定一個平面。因此,具有三個可調支承點的調平機構是一種自然的設計方案,一個容易忽視的問題是:三點支承平臺屬于欠約束、欠驅動系統。在自然狀態下仍具有某些自由度,平臺的穩定性差,不利于設備的精度保持;在輸入狀態下,平臺處于欠驅動狀態,為實現平臺調平,需要考慮平臺運動的幾何因素及平臺支承與底面之間的摩擦力,在控制上比較復雜[4-5]。針對這一問題,提出了一種雙驅動六點支承平臺,并介紹了該平臺的調平算法及實驗結果。
1 雙驅動六點支承平臺
歷史上有兩種六點支承夾具,分別稱為3V夾具和Kelvin夾具[6-7],如圖1和圖2所示。
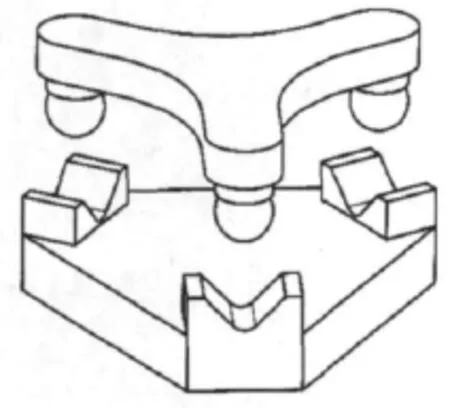
圖1 3V夾具Fig.1 3Vclamp
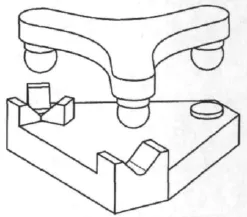
圖2 Kelvin夾具Fig.2 Kelvin clamp
這兩種夾具主要用于精密定位,已經存在100多年了。它們在自然狀態下均具有確定位姿,不存在三點支承結構的欠約束問題。因此,考慮用它來做調平機構的支承。然而這兩種夾具均是圓周對稱結構,加入三個螺旋輸入后,在調平時會出現運動干涉,而使用正交結構則有可能避免這一問題。鑒于這些原因,提出了雙驅動六點支承平臺結構,如圖3所示。
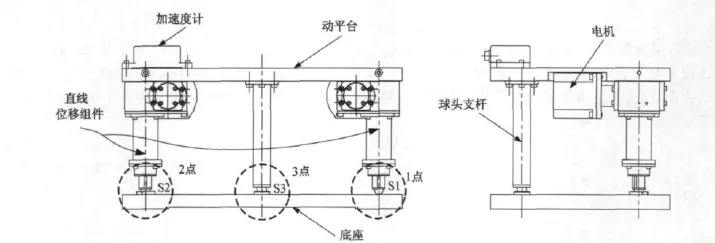
圖3 雙驅動六點支承平臺Fig.3 Leveling stages with six-point supports and two inputs
該平臺僅具有兩個直線位移輸入組件,減少了驅動元件的數目。所謂六點是指球頭S1與平面形成一點接觸,S2與V型槽形成兩點接觸,S3與錐孔形成3個非冗余約束點,由此形成六個非冗余接觸點。這種約束模式保證了機構的確定位姿和確定運動,由此解決了三點支承平臺的欠約束和欠驅動問題。需要說明的是這里的六點是指六個非冗余約束點。
在結構上,雙驅動六點支承平臺包括動平臺、底座、加速度計、直線位移組件以及球頭支桿。在電機的驅動下,直線位移組件的球頭支承產生直線位移,用以驅動平臺轉動。球頭支桿的球頭與底座上的錐孔構成平臺的運動支點。
2 調平算法
調平的目的是使儀器工作的基準面與水平面重合。所謂水平面是指與重力加速度方向垂直的平面。因此,調平本質上是使平臺的法線與重力加速度方向重合。從這一角度出發,本文提出一種基于重力加速度方向矢量的調平算法。如圖4所示平臺處于水平狀態,則平臺法線矢量N與重力加速度方向矢量G重合。如圖5所示平臺處于非水平狀態。此時平臺的法線矢量N與重力加速度矢量G之間存在一個夾角。本質上,如果使平臺的法線矢量與重力加速度矢量重合,那么就實現了調平。因此,無需直接關注平臺的運動變化,而僅需關注平臺的法線矢量與重力加速度矢量是否重合,由此將平臺的調平問題轉化為平臺法線矢量的空間運動變換問題。
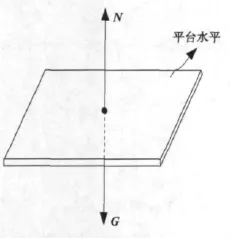
圖4 平臺水平狀態Fig.4 Leveling conditions of stages
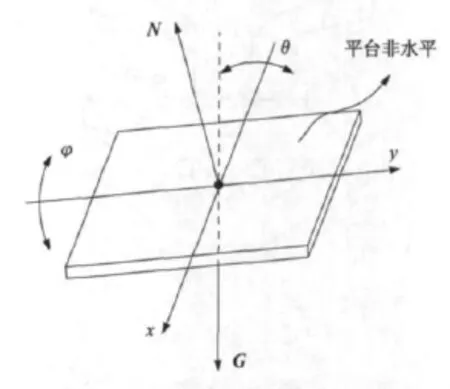
圖5 平臺傾斜狀態Fig.5 Tilt conditions of stages
設平臺的法線矢量N和重力加速度矢量G分別為:

設存在過渡矢量M,則平臺法線矢量N繞x軸轉動θ到過渡矢量M,然后過渡矢量M繞y軸轉動φ到重力加速度矢量G。且設過渡矢量M=(mxmymz)T,分別確定平臺法線矢量N和過渡矢量M 在x軸的投影,過渡矢量M和重力加速度矢量G在y軸的投影。令X0和Y0分別表示x軸和y軸方向的單位矢量,則:

可得:

則:

由此可得過渡矢量:

設法線矢量N繞x軸轉動θ到過渡矢量M,然后過度矢量M繞y軸轉動φ到重力加速度矢量G,PX與QX分別是N和M 在垂直于x軸方向平面的投影,則:
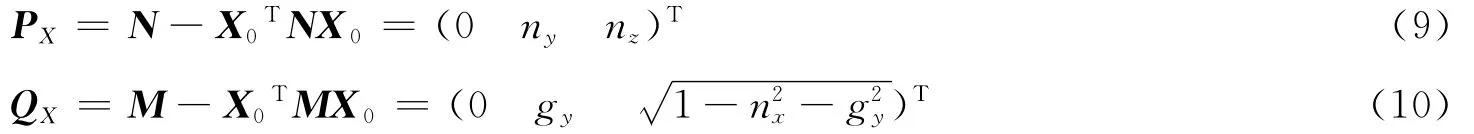
可得轉動角度θ:
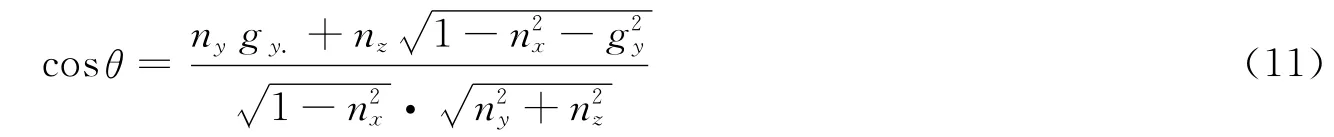
同理,設PY和QY分別是M 和G在垂直y軸方向平面的投影,則
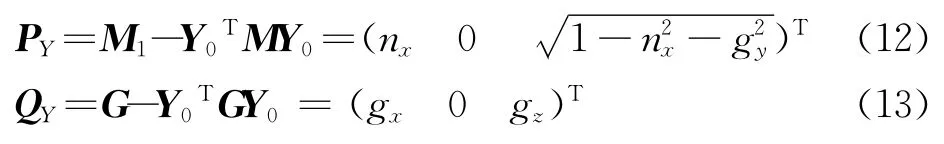
可得轉動角度φ:
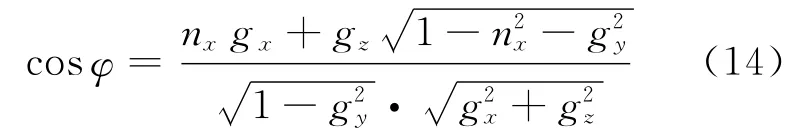
轉角θ和φ的存在證明了僅通過兩個輸入可以實現平臺的調平,同時給出了實現調平的轉動角度。
在此基礎上編寫了調平軟件,軟件主要包括控制卡初始化,數據采集、平臺轉角等程序模塊。通過調用初始化函數可對控制卡進行初始化;數據采集模塊的功能是為了獲取平臺的重力加速度數據;平臺轉角模塊可使系統根據轉角并通過脈沖當量計算電機需要發送的脈沖數。調平程序流程如圖6所示。
當平臺傾角不大于0.002°時即認為平臺達到水平,并以此作為程序的判斷條件。
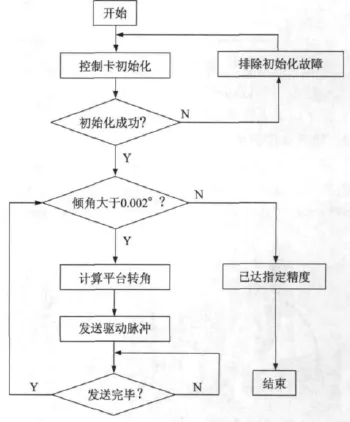
圖6 調平程序流程圖Fig.6 Flow chart of leveling program
3 調平實驗
調平實驗旨在驗證兩輸入調平算法,并對平臺重復精度進行測試。調平實驗系統主要包括平臺本體、加速度計、步進電機、驅動器、控制卡以及PC機。將加速度計量值通過三角關系轉化可得角度值,傾角模型如圖7所示。
3.1 兩輸入調平算法驗證
首先通過傳感器測量平臺當前的傾角θx和θy,可以將加速度計量值轉化為傾角;然后,根據雙輸入調平算法可計算兩驅動器的直線位移Δlx和Δly。那么,當兩直線驅動器相應的伸長或縮短Δlx和Δly時,理論上,平臺應達到水平,即平臺此時的傾角Δθx和Δθy應等于零。考慮到零件加工以及傳動誤差等因素,傾角Δθx和Δθy應接近于零。為此,對平臺隨機測量10次,實驗數據如表1所示。
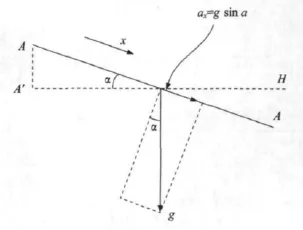
圖7 傾角模型Fig.7 The tilt model
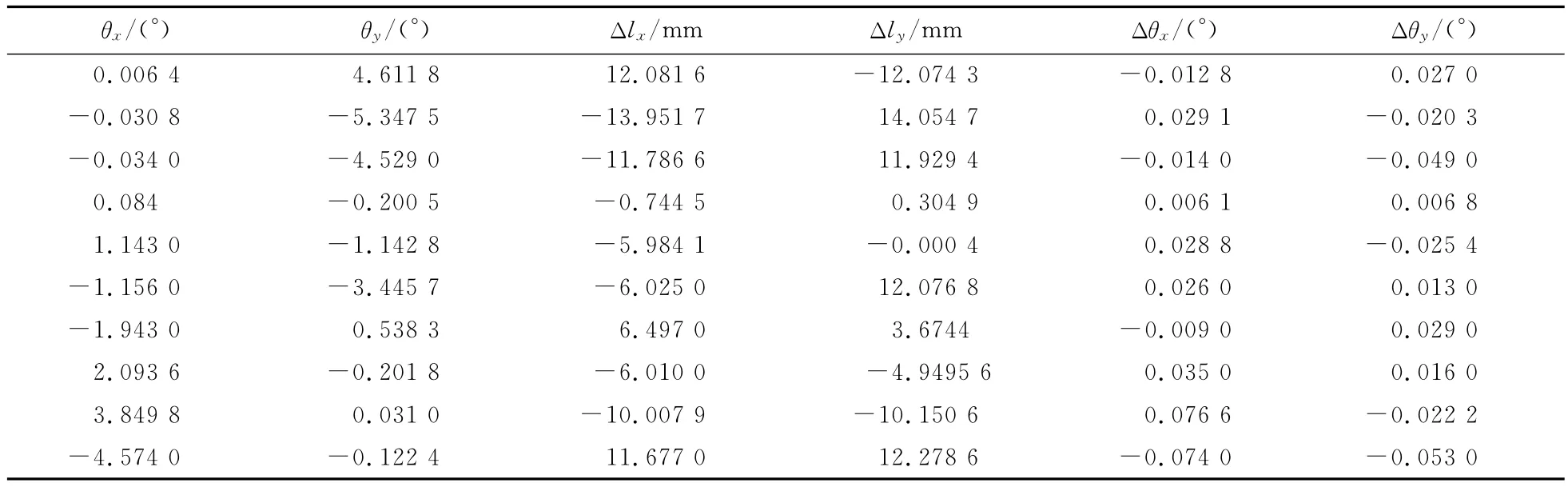
表1 兩輸入調平算法驗證數據Tab.1 The validation data of leveling algorithm using two inputs
由表1可以看出,平臺在一定的傾角θx和θy下,輸入一次位移控制量移Δlx和Δly后,平臺傾角Δθx和Δθy趨近于零,這表明算法具有較好的收斂性。如通過閉環控制,則可使平臺達到指定的水平精度,由此驗證了兩輸入調平算法的正確性。
3.2 重復精度測試
調平平臺實驗系統主要包括平臺機械本體、加速度計、步進電機、驅動器、控制卡以及PC機。實驗中分為兩個測試狀態。測試狀態1是指將兩直線位移組件的球頭均調至最高點,如圖8所示。測試狀態2是指將一個直線位移組件的球頭調至最高點,另一個直線位移組件的球頭調至最低點,如圖9所示。

圖8 測試狀態1Fig.8 Testing condition 1
圖9 測試狀態2Fig.9 Testing condition 2
在每組狀態下,依次使球頭變化3mm,連續測試6組數據,兩個狀態所測得數據如表2和表3所示。
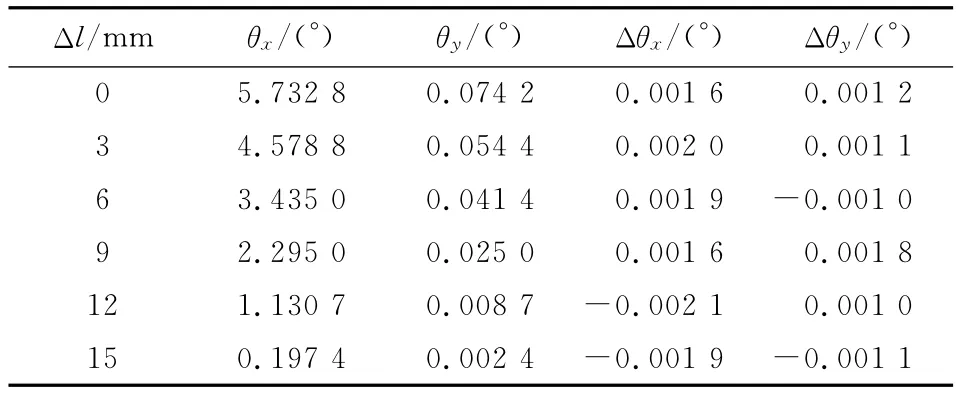
表2 最高點狀態Tab.2 Condition of highest points
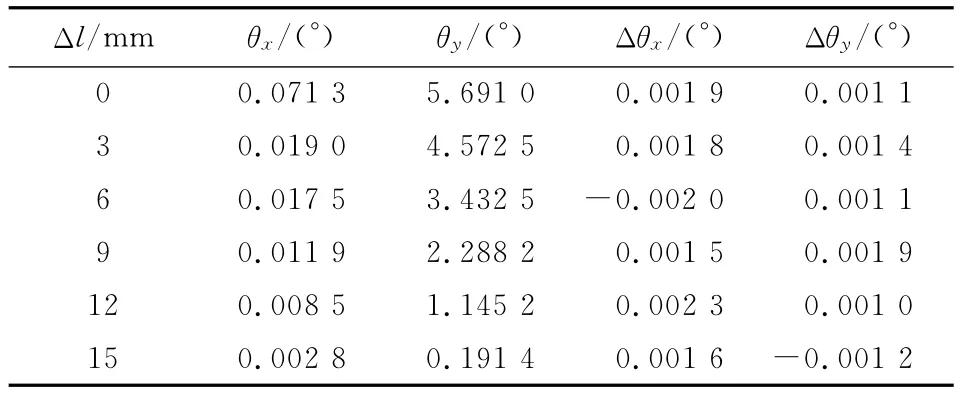
表3 最高點和最低點狀態Tab.3 Condition of highest points and lowest points
平臺在兩個方向的重復精度分別為σx=0.001 7°和σy=0.001 1°,兩個方向的水平重復精度優于0.001 7°。
4 結 論
雙驅動六點支承平臺采用機電式自動調平,水平重復精度優于0.001 7°,調平范圍 ±5°。相比于三點支承平臺,該平臺具有如下幾個特點:
(1)六點支承結構,即在自然狀態下具有確定位姿,在輸入狀態下具有確定運動,由此解決了傳統三點支承平臺的欠約束和欠驅動問題;
(2)僅使用兩個驅動,并可聯動輸入進行調平,減少了驅動元件的數目,簡化了系統的結構;
(3)使用加速度計作為傳感元件,相對于傾角傳感器,該方法更加簡單、響應速度快;
(4)重力加速度矢量調平算法具有物理概念清晰,數學方法嚴格的特點,可準確建立平臺的運動模型。
此外,本文的工作深化了對調平問題的認識,分析了“三點確定一個平面”與“調平”的問題。三點可以確定一個平面,但這并不意味著調平需要使用三個腳螺旋。三點確定一個平面僅是一個幾何概念,它與物體的調平是不同的兩個問題。從運動學的角度,調平是對物體兩個轉動自由度的調整。
雙驅動六點支承平臺是一種新型二自由度球面并聯機構,動平臺的運動屬于二自由度定點運動。由于光束在空間的指向僅需兩個參數即可確定。因此,平臺的這種二自由度定點運動對光束的指向控制具有潛在的應用價值。例如用作大口徑反射鏡架[8-10]或并聯光電跟蹤平臺等,未來將就這方面的研究進行報道。
[1]姜偉偉,高云國,馮棟彥.大型光電設備基準平面自動調平系統[J].光學 精密工程,2009,17(5):1039-1045.
[2]高福暉.機械零件強度許用值新標準及大型經緯儀機械設計[M].成都:成都科技大學出版社,1998:202-210.
[3]李勇建,魏貴玲,鄧勁松,等.自動調平技術研究[J].壓電與聲光,2010,32(6):949-952.
[4]王大志.應用運動學原理的雙驅動六點支承平臺設計與調平方法研究[D].北京:中國科學院研究生院,2012.
[5]王大志,何 凱,杜如虛.精確約束二自由度微動角位移機構設計[J].光學 精密工程,2011,19(8):1874-1882.
[6]HALE L C,SLOCUM A H.Optimal design techniques for kinematic couplings[J].Precision Engineering,2001,25(2):114-127.
[7]SLOCUM A H.Precision machine design[M].Michigan:Prentice-Hall Inc.,1992.
[8]朱耆祥.ICF用陣列鏡腔及陣列伺服反射鏡的新型反射鏡結構[J].光電工程,2001,28(5):24-27
[9]章亞男,沈麗麗,沈衛星,等.大口徑透鏡姿態調整機構的支承分布[J].光學 精密工程,2010,18(12):2624-2632.
[10]沈麗麗,章亞男.大口徑非圓透鏡的夾持設計[J].光學儀器,2011,32(5):49-53.

