水下聲自導武器目標跟蹤方法研究

楊向鋒，楊云川，陳亞林

中國船舶重工集團公司 第705研究所，西安 710075

1 引言

目標跟蹤是水下聲學觀測系統的重要功能之一，卡爾曼濾波方法是進行目標跟蹤的主要方法[1]，利用卡爾曼濾波方法對水下目標進行跟蹤近年來得到了廣泛的研究[2-6]，但主要是針對水下聲學觀測系統基于被動觀測方式的純方位目標跟蹤方法研究，其觀測平臺靜止或按固定航路低速運動，其采樣間隔固定。水下聲自導武器因其多采用主動觀測方式并且具有高速運動特性，其目標跟蹤方法研究不多。水下聲自導武器工作在主動方式時，通過發射聲信號并接收目標反射信號對目標進行檢測、參量估計，獲得目標相對的空間信息后通過彈道機動向目標運動，在向目標運動過程中繼續進行檢測、參量估計、按一定規律調整運動方向跟蹤目標，由此可見水下聲自導武器作為觀測平臺一直處于高速機動狀態。在作戰過程中，水下聲自導武器與目標的相對位置不斷變化，水下聲自導武器會根據與目標的距離實時調整探測波形和檢測周期，同時水下聲自導武器進行彈道機動時需要一定的時間實現，最終導致其采樣間隔處于變化之中。綜合以上兩方面的因素，水下聲自導武器跟蹤目標的過程表現為一個動基座時變過程。本文主要研究水下主動聲自導武器標跟蹤問題，分析了水下主動聲自導武器的工作特點并建立了水下主動聲自導武器主動目標跟蹤模型，對跟蹤模型進行了仿真實驗。

2 跟蹤建模

卡爾曼濾波方法對目標進行跟蹤時，要求目標的多次觀測必須處于同一個觀測坐標系下，而采樣間隔必須是確知的，因此水下聲自導武器利用卡爾曼濾波方法對目標進行跟蹤必須解決基座運動和觀測時變的問題。

2.1 坐標變換

定義O1x1y1z1為水下聲自導武器坐標系，原點O1為水下聲自導武器質心，軸向指向頭部方向為O1x1軸，O1y1軸垂直于O1x1并指向正上方，O1z1軸垂直于O1x1z1平面并符合右手坐標系[7]；空間任一點目標在水下聲自導武器坐標系中的檢測信息為(r,α,β)，如圖1所示。

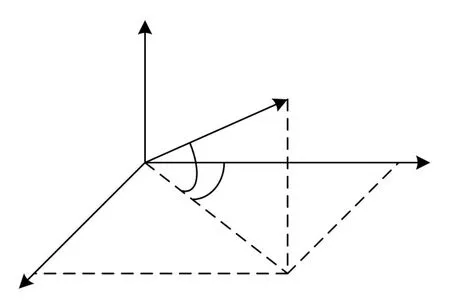
圖1 水下聲自導武器坐標系

由幾何關系可知其水下聲自導武器坐標系的坐標計算公式如下：

定義O xyz為大地坐標系，原點O為發射點，O y軸垂直向上，Ox軸為發射方向，Oz軸垂直于Oxy平面并符合右手坐標系[8]；水下聲自導武器作為一個具有六自由度的剛體，其坐標系相對于大地坐標系的位置就由六個坐標來確定，即水下聲自導武器坐標系原點在大地坐標系中的坐標(x0,y0,z0)和水下聲自導武器坐標系與大地坐標系之間的三個夾角(ψ,θ,φ)。三個角度分別表示水下聲自導武器的偏航角ψ、俯仰角θ和橫滾角φ，偏航角從尾部看向左為正，俯仰角向從尾部看向上為正，橫滾角從尾部看向右為正，水下聲自導武器坐標系與大地坐標系的旋轉關系如圖2所示。

由幾何關系可知，水下聲自導武器坐標系到大地坐標系的旋轉轉換矩陣可以表示為：

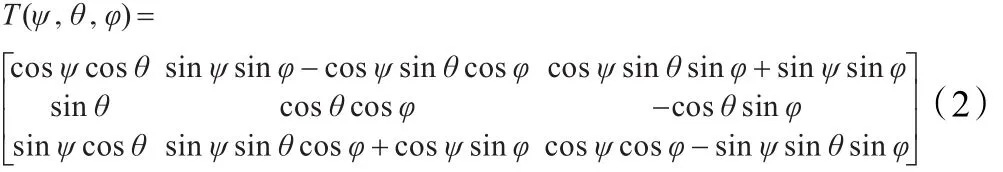
若水下聲自導武器坐標系原點在大地坐標系中的坐標為(x0,y0,z0)，與大地坐標系之間的三個夾角為(ψ,θ,φ)，則水下聲自導武器坐標系中任一點目標(x1,y1,z1)在大地坐標系下的坐標(x,y,z)可以表示為：

水下聲自導武器導航定位系統可以實時提供其在大地坐標系的六個坐標(x0,y0,z0,ψ,θ,φ)，通過坐標變換將目標坐標從水下聲自導武器坐標系變換到大地坐標系，解決了觀測基座運動的問題。坐標變換使得目標的多次觀測處于同一個觀測坐標系下，滿足卡爾曼濾波器觀測平臺靜止的要求。

2.2 目標狀態方程

對水下目標而言，在未受到攻擊時，在水下可能靜止或勻速運動；在受到水下聲自導武器攻擊時的運動不外乎加速、轉彎、下潛等，在運動過程中其加速度一般恒定或變化不大可認為恒定，因此目標的坐標方程、速度方程、加速度方程如下：

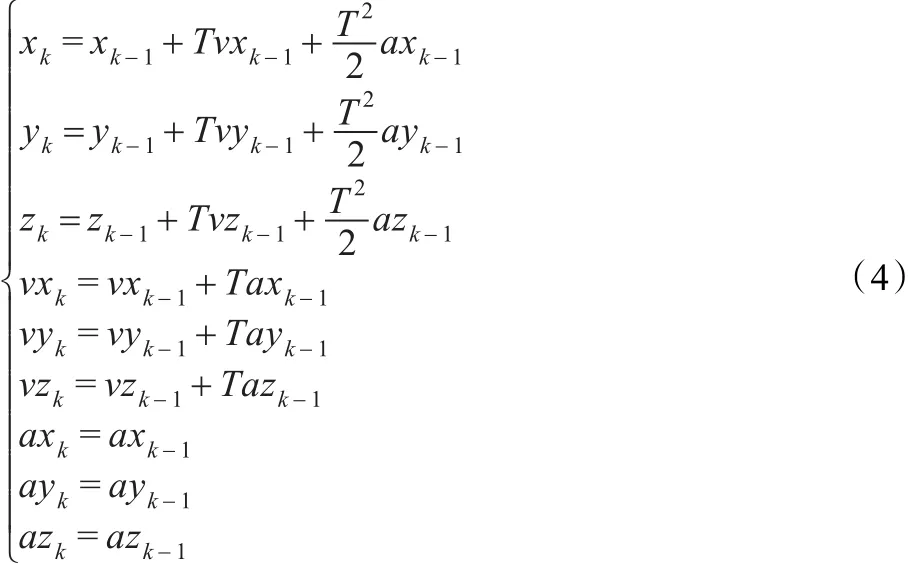
式中，xk、yk、zk，vxk、vyk、vzk，axk、ayk、azk分別是目標在大地坐標系x軸、y軸、z軸上的坐標、速度、加速度，T是采樣周期。

水下聲自導武器攻擊目標的過程是一個時變過程，相鄰兩次檢測之間可能存在水下聲自導武器彈道的變換過程，同時根據自導系統配置可能存在周期時間調整，而且在自導工作過程中可能出現某周期丟失目標，下周期又檢測到目標的情況，即式（4）中的T是變化的，而卡爾曼濾波方法要求系統采樣周期必須是確知且等間隔，T變化導致狀態轉移矩陣不確定，因此無法直接使用卡爾曼濾波方法。

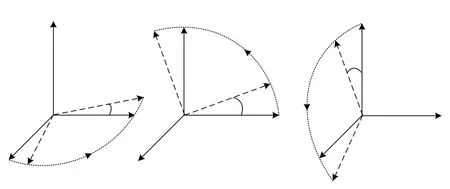
圖2 水下聲自導武器坐標系與大地坐標系的旋轉關系

水下聲自導武器自導系統可以在統一時鐘下提供每次檢測的精確時間，采樣周期可以通過相鄰兩次觀測的時間進行實時計算，即

tk為第k次觀測時間，通過實時計算采樣周期Tk,k-1就解決了觀測時變問題。實時計算采樣周期Tk,k-1后，雖然不能滿足標準卡爾曼濾波方法對采樣周期等間隔的要求，但狀態轉移矩陣可以利用Tk,k-1進行實時計算，能滿足卡爾曼濾波方法遞推計算的需要。

2.3 跟蹤模型

水下聲自導武器攻擊目標的過程相對短暫，可以忽略外界的環境對目標運動的干擾，選擇目標在大地坐標系x軸、y軸、z軸上的坐標、速度、加速度為狀態向量。

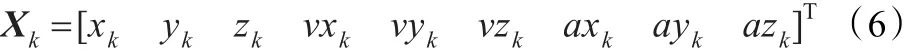
則狀態方程及狀態轉移矩陣可表示為：

水下聲自導武器檢測目標是直接測量，考慮到測量噪聲nk，觀測方程可表示為：

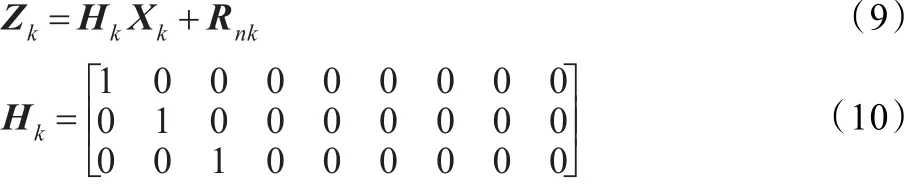
得到狀態方程和觀測方程后就可以給出Kalman濾波的遞推公式如下：

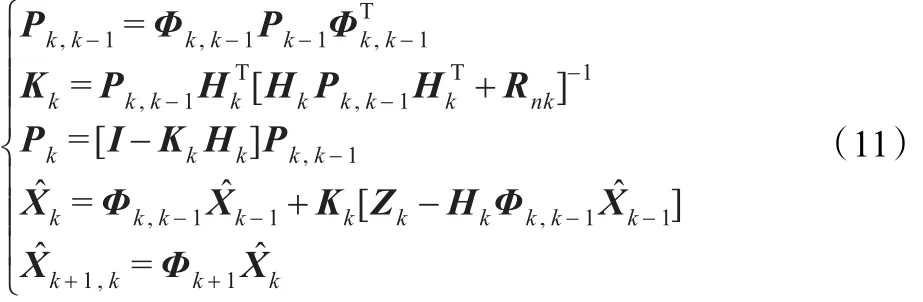
該模型為了降低復雜度而忽略了外界的環境對目標運動的干擾以及假設運動過程中其加速度恒定，該簡化近似可能導致系統模型的不準確。卡爾曼濾波是無限增長記憶的濾波，k時刻的最優估計要用到k時刻以前的全部觀測數據，隨著k的增大，濾波值中的老數據比重太大，而新數據比重太小，當系統存在模型誤差和計算誤差時，新的觀測數據對修正狀態估計的作用太小，不能有效地抑制誤差對狀態估計值的影響，從而導致卡爾曼濾波精度下降甚至濾波發散。為了減小模型的不準誤差，人們對傳統的增長記憶卡爾曼濾波器進行了改造[8-9]，衰減記憶卡爾曼濾波器便是比較成功且易于實現的一種改進方法。

在Kalman遞推公式（11）中，計算 Pk,k-1時以 S Pk-1替代Pk-1，S稱為衰減因子。當S＞1時，當前數據的作用得到加強，歷史數據的作用隨著遞推計算慢慢弱化，實際應用中衰減因子的選取對濾波結果產生很大影響，若采取固定值的方法，在一些情況下可能會發生異常，甚至導致濾波發散。文獻[8]利用新息序列與量測值匹配程度自動調整衰減因子取得較好的結果，本文利用目標坐標量測值與坐標濾波估計值的匹配程度自動調整衰減因子，自適應約束條件如下：

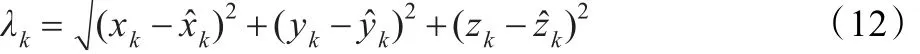
式中，xk、yk、zk為 k 時刻坐標量測值，?、、為 k 時刻坐標濾波估計值。

k+1時刻的衰減因子Sk+1按下式選取：

式中，a為一個正實數，λ為判別門限。

如果濾波正常，則經過濾波得到的坐標濾波估計值與坐標量測值在一定誤差范圍內是匹配的，此時取Sk=1，在k時刻不進行衰減記憶濾波；如果濾波異常或發散，則經過濾波得到的坐標濾波估計值與坐標量測值會出現較大的偏差，此時取Sk=aλ＞1，在k時刻進行衰減記憶濾波，使得新數據對狀態估計的修正得到加強。

在工程上通常以初次檢測值為坐標初值并認為初始速度和加速度為零，若初次檢測值為[x0,y0,z0]，則狀態變量初值如下：

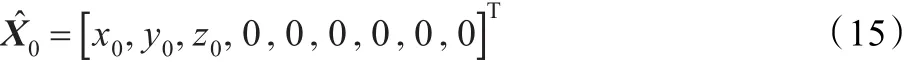
式（9）的Rnk是量測誤差矩陣，反映水下聲自導武器檢測造成的誤差，與檢測算法、信號波形、頻帶及水聲環境等有關，本文根據工程經驗按下式選取。

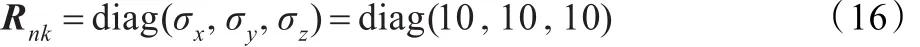
根據上式可知：

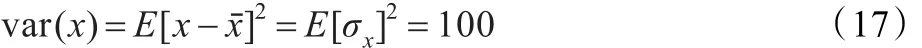
由于任意兩次觀測相互獨立，所以有：

由式（17）、（18）、（19）可知：

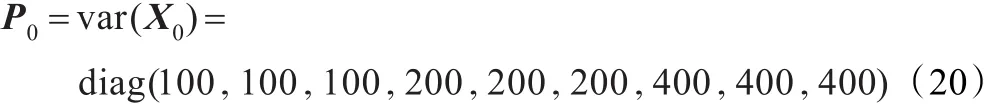
衰減因子選擇的判別門限λ反映的是量測值與濾波估計值匹配時的偏差，可以依據量測值的方差選擇，文中給出了量測值的方差工程經驗值σx,σy,σz，λ按下式計算：

已知觀測值（水下聲自導武器檢測值經過坐標變換）Zk、觀測時間tk，本文提出的水下聲自導武器自適應衰減記憶Kalman濾波跟蹤算法流程如圖3。

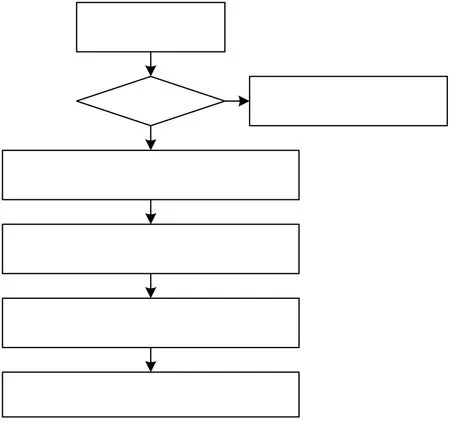
圖3 自適應衰減記憶Kalman濾波跟蹤算法流程圖

3 仿真實驗與分析

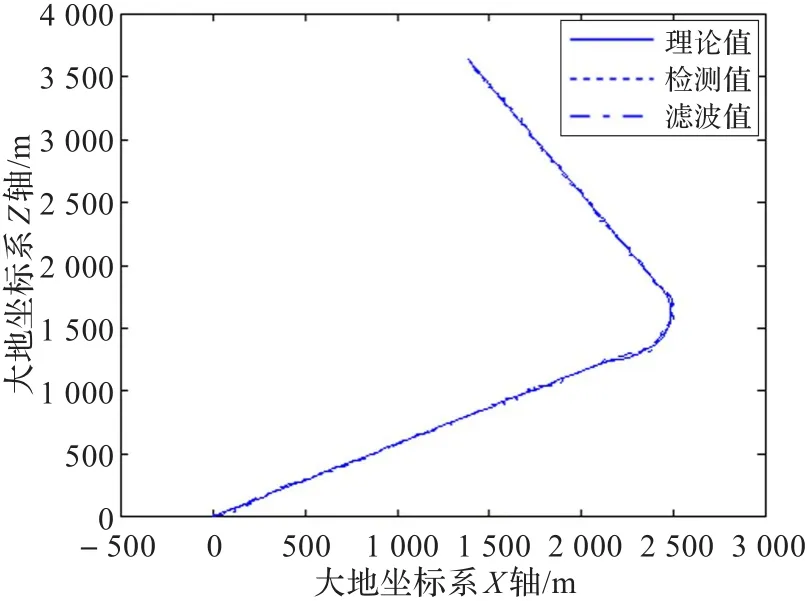
圖4 自適應衰減記憶Kalman濾波跟蹤結果

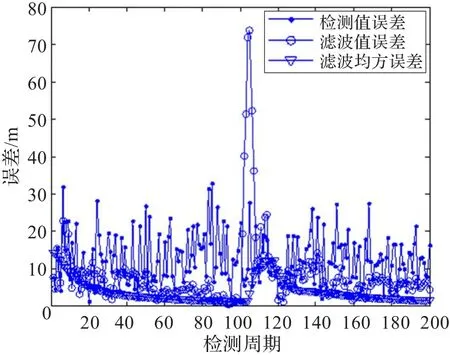
圖6 自適應衰減記憶Kalman濾波誤差曲線

為了驗證跟蹤模型的有效性，進行了數學仿真實驗。目標以大地坐標系原點為起點，先在Oxz平面以5 m/s的速度沿與x軸夾角30o方向勻速直線運動，一段時間后以0.43 m2/s的加速度加速并以7.5o/s的角速率逆時針轉彎，加速到10 m/s，運動方向轉到與x軸夾角150o方向時勻速直線運動；采樣間隔在完成轉彎前為5 s加入方差為2 s隨機高斯分布噪聲，完成轉完后為3 s加入方差為1 s隨機高斯分布噪聲，目標量測值根據采樣間隔計算得到的理論值加入方差為10 m的隨機高斯分布噪聲。濾波初值=[0,0,0,0,0,0,0,0,0]T,P0=diag(100,100,100,200,200,200,400,400,400),Rnk=diag(10,10,10)，衰減因子初值S0=1，計算Sk+1時a=0.01，λ=30.0。該數據樣本模擬了水下聲自導武器檢測并跟蹤目標的典型過程，開始水下聲自導武器距離目標較遠，檢測周期較長，水下聲自導武器跟蹤目標一段時間后，目標開始通過加速轉彎方式進行機動逃逸，此時水下聲自導武器已經距離目標較近，檢測周期縮短。數據樣本由計算機模擬生成，分別應用本文提出自適應衰減記憶Kalman濾波跟蹤算法和普通Kalman濾波跟蹤算法對該數據樣本進行了計算機仿真對比實驗，跟蹤及運動參數估計結果如圖4～11所示。

仿真結果表明，在轉彎之前的勻速直線運動過程中，自適應衰減記憶Kalman濾波與普通Kalman濾波實際上是相同的，經過10個觀測周期約50 s后濾波誤差明顯小于原始檢測值誤差，運動學參數估計值收斂于數據樣本設計值，而傳統的純方位目標跟蹤方法一般需要數百秒的時間才能完成跟蹤收斂。在加速轉彎過程及之后的勻速直線運動過程中，兩種濾波方法的濾波結果出現了明顯的差異，雖然自適應衰減記憶Kalman濾波在加速轉彎期間出現了較大的誤差，但是通過進行自適應衰減記憶，在完成加速轉彎后，經過10個觀測周期約30 s后很快再次跟蹤上目標，其運動學參數估計二次收斂，估計值正確，而普通Kalman濾波從轉彎開始濾波出現了發散，不僅沒有跟蹤上目標，而且運動學參數估計錯誤。自適應衰減記憶Kalman濾波跟蹤方法與傳統的純方位目標跟蹤方法相比具有較快的收斂速度，與普通Kalman濾波跟蹤方法相比具有較強的機動目標跟蹤能力。

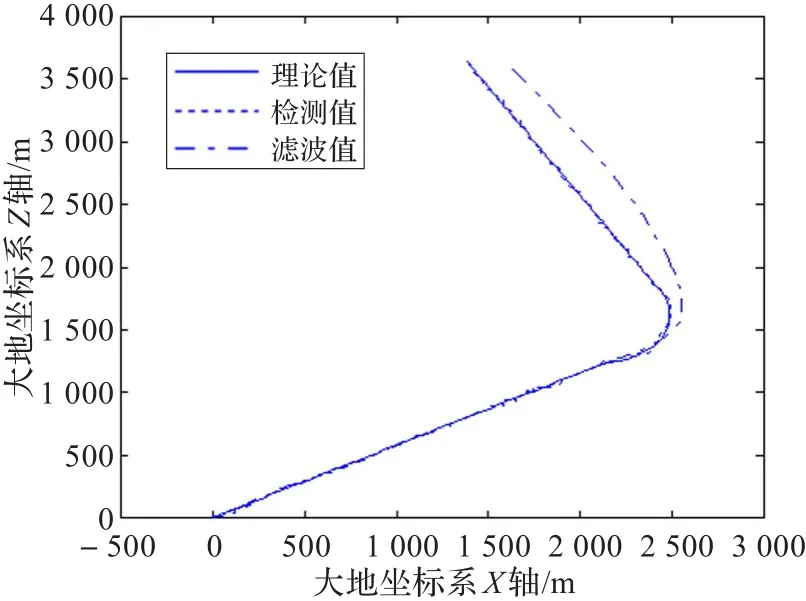
圖5 普通Kalman濾波跟蹤結果

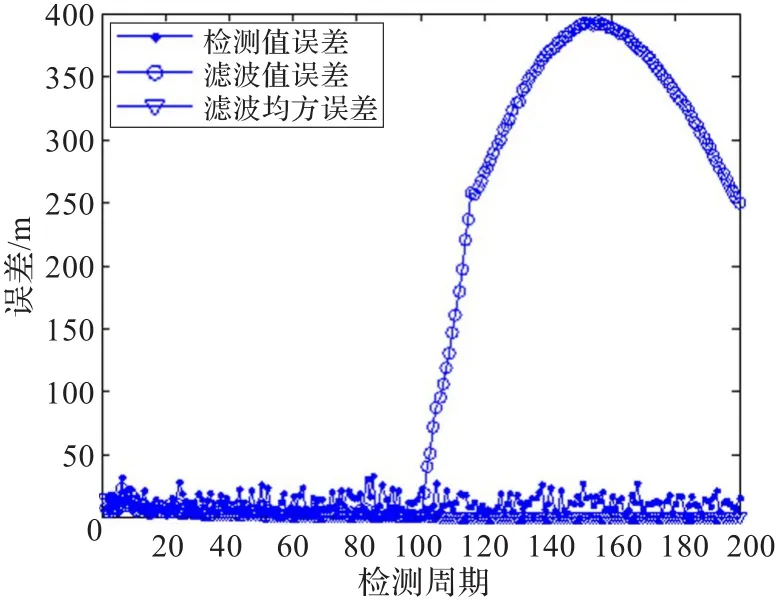
圖7 普通Kalman濾波誤差曲線

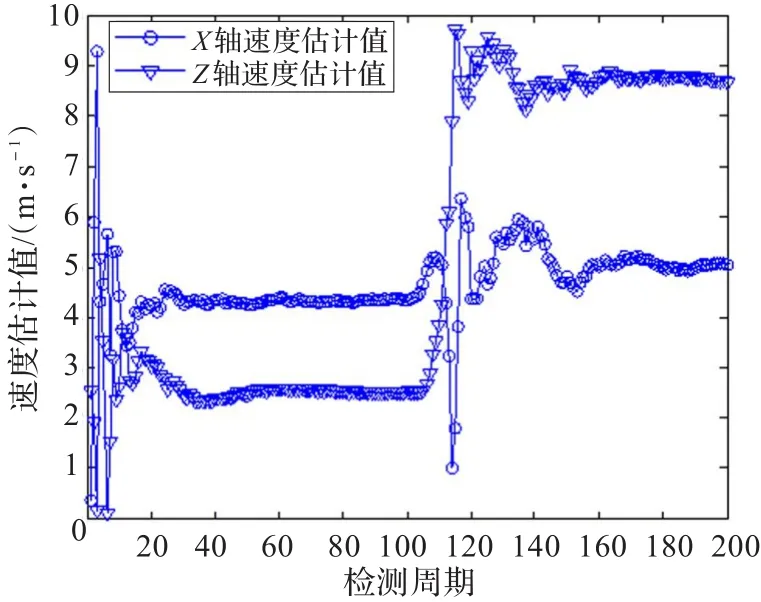
圖8 自適應衰減記憶Kalman濾波速度估計結果

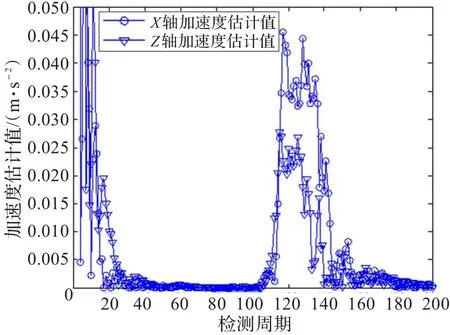
圖10 自適應衰減記憶Kalman濾波加速度估計結果

4 結束語

主動水下聲自導武器根據目標檢測信息將自身導向目標的過程中一直處于高速機動狀態，水下聲自導武器變換檢測周期、實施彈道機動以及受水聲環境影響某周期丟失目標后下周期又檢測到目標均會導致其觀測時變。本文通過分析主動水下聲自導武器的工作特點，通過坐標變換及實時計算采樣時間解決了其觀測基座運動和觀測時變的問題，并建立了基于自適應衰減記憶Kalman濾波的主動水下聲自導武器目標跟蹤模型，給出了濾波初值在工程應用中的選取方法，仿真實驗證明自適應衰減記憶Kalman濾波算法不僅具有較快的收斂速度和較高的運動學參數估計精度，而且能有效地跟蹤高速機動目標，具有一定的工程應用價值。

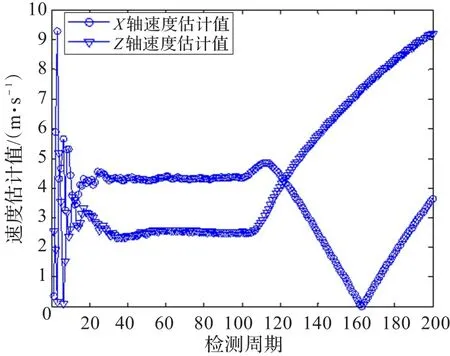
圖9 普通Kalman濾波速度估計結果

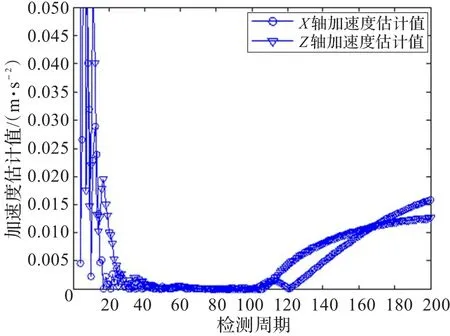
圖11 普通Kalman濾波加速度估計結果

[1]權太范.目標跟蹤新理論與技術[M].北京：國防工業出版社，2009.

[2]劉偉，王昌明，趙輝.基于卡爾曼濾波的水下近距目標運動分析[J].彈道學報，2008，20（4）：28-31.

[3]吳盤龍，孔建壽.基于平方根UKF的水下純方位目標跟蹤[J].南京理工大學學報：自然科學版，2009，33（6）：751-755.

[4]石章松，劉忠.單站純方位目標多模型卡爾曼濾波跟蹤算法的研究[J].系統仿真學報，2006，18（7）：1802-1805.

[5]曲毅，劉忠，屈津竹.基于時延的水中目標純方位跟蹤算法[J].系統工程與電子技術，2007，29（1）：107-109.

[6]葉靈軍，曲毅，劉忠，等.水下純方位目標運動分析的UKF濾波算法[J].火力與指揮控制，2009，34（8）：132-134.

[7]嚴衛生.魚雷航行力學[M].西安：西北工業大學出版社，2005.

[8]劉健，劉忠，曲毅.純方位目標運動分析的自適應衰減記憶濾波算法[J].中國海洋大學學報，2006，36（4）.

[9]章飛，周杏鵬，陳小惠.基于衰減記憶濾波的平方根UKF被動目標跟蹤算法[J].測控技術，2010，29（4）：22-26.