蒙特卡羅模擬在財務預測中的運用
上海愛爾眼科醫院 陸靜
財務工作者不可避免地在工作中需要根據企業過去一段時期財務活動的資料,結合企業現在面臨和即將面臨的各種變化因素,運用數理統計方法,以及結合主觀判斷,來預測企業未來財務狀況。財務預測過程是對未來的展望和規劃的過程,也是增強企業在執行戰略計劃信息的有效途徑。
企業進行經營決策時,必然要涉及成本費用、收益以及資金需要量等問題,而這些大多需要通過財務預測進行估算。因此,財務預測直接影響到經營決策的質量。同時,財務預測中涉及大量的科學方法以及現代化的管理手段,財務預測與分析能力,將直接影響企業應變求存的能力。準確性越高,作用越大;反之,則越小。
1 傳統財務預測的方法及弊端
傳統財務預測主要分為定性預測和定量預測。定性預測是建立在經驗判斷、邏輯思維和邏輯推理基礎之上的,其主要特點是利用直觀的材料,依靠個人經驗的綜合分析,對事物未來狀況進行預測。定量預測是通過分析事物各項因素、屬性的數量關系進行預測的方法。它的主要特點是根據歷史數據找出其內在規律、運用連貫性原則和類推性原則,通過數學運算對事物未來狀況進行數量預測。在預算編制方法的選擇上,多數企業仍采用傳統的固定預算、定期預算等方法編制,所有的預算指標在執行過程中都保持不變,運行結束時將結果直接與預算指標進行比較。這種靜態預算編制方法適用于業務量波動不大的企業。當企業銷售量、價格和成本等因素變化較大時,靜態預算指標則表現出盲目性、滯后性和缺乏彈性,難以成為考核和評價員工的有效基準。
為了彌補這些缺陷,企業通常會使用敏感性分析(Sensitivity Analy. sis)和場景分析(Scene Analysis)。然而,這種分析在現實世界中也存在一定的局限性。敏感性分析只允許在同一時間只能有一個變量在變化;場景分析則要求多個變量間存在特定的關聯關系。比如通貨膨脹因素、政府投資額和競爭者數目,顯然也不能包括所有的變量因素。
我們設計財務預測模型的目的是為了滿足企業現實的管理需求,預測需要建立在各項參數動態的情形之上,將各項可能發生的事件應用隨機數來進行計算機模擬,同時展現該事件發生時出現的結果及累計概率分布,使得企業能做好充分的應對準備,而通過蒙特卡洛模擬方法恰能實現此項目標。
2 蒙特卡羅方法簡介
蒙特卡羅(Monte Carlo)方法于20世紀40年代由美國在第二次世界大戰中研制原子彈的“曼哈頓計劃”計劃成員S.M.烏拉姆和J.馮·諾伊曼首先提出。數學家馮·諾伊曼用馳名世界的賭城——摩納哥的Monte Carlo——來命名這種方法,為它蒙上了一層神秘色彩。其是一種應用隨機數來進行計算機模擬的方法,此方法對研究的系統進行隨機觀察抽樣,通過對樣本值的觀察統計,求得所研究系統的某些參數。
基于Excel的蒙特卡羅模擬實現步驟如下:(1)建立數學模型;(2)收集模型中風險變量的數據,確定風險因素的分布模型;(3)確定模擬次數、產生隨機數;(4)由產生的隨機數在各風險變量的分布函數中隨機抽樣,帶入模型求出目標變量的一個樣本值;(5)重復第4步N次,產生N個樣本值,對得到的N個樣本值進行統計分析。
3 蒙特卡羅模擬財務預測實證
案例:產品A的銷售額主要受行業整體銷量、市場份額、銷售單價影響,產品A的年銷售額=整個行業產品A的銷售量×該企業產品A的市場份額×產品A的單位價格。
對下一年整個行業的銷售量做以下分布預測:

表1
下一年市場份額的概率分布:

表2
產品A單位價格模型=190+2×行業總銷售量(單位:百萬)±3(即50%的幾率出現+3元,50%的幾率出現-3元 )
要求:預測下一年企業產品A的銷售額。
3.1 在Excel中建立已知數據,建立數據模型
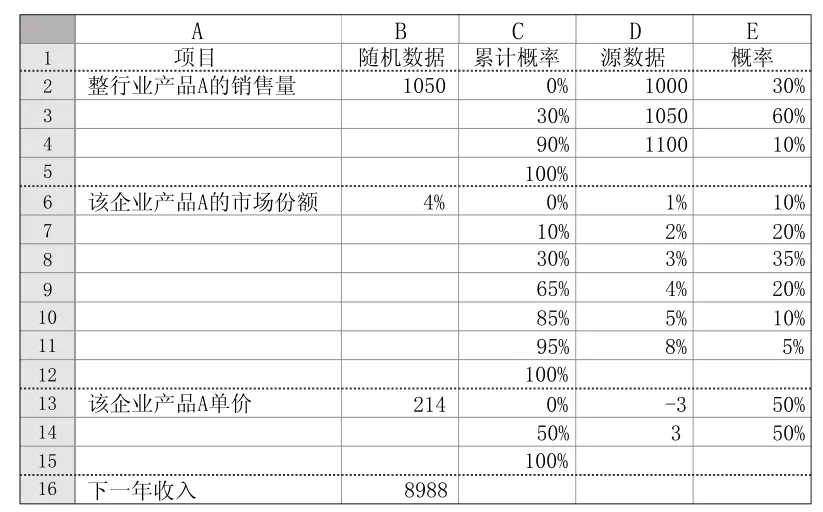
圖1
利用Excel的VLOOKUP和RAND函數,聯合使用生成具有給定概率分布的隨機變量的觀測值,在本例中三個不可控的隨機變量分別為:整個行業產品A的銷售量、該企業產品A的市場份額、該企業產品A的單價,由這三個指標相乘得出了該企業A產品下一年的收入。
關鍵指標公式輸入如下:

表3
3.2 對該企業產品A的下一年收入進行模擬運算
在空白區域創建一個模擬運算表,運用Excel的自動填充功能,生成一個起始為1,終止值為5000,步長為1的等差數列,以此表示模擬實驗中的不同序列號,利用模擬運算表功能得出了隨機5000次后該企業下一年產品A的銷售收入。
3.3 統計分析
對模擬運算表隨機產生的5000組數據統計分析,利用AVE RAGE、STDEV、MAX、MIN函數進行基礎分析,得出數據如下:

表4
(1)平均值:表示的是該企業A產品下一年收入的平均值;(2)標準差:表示的是各數據偏離A產品下一年收入平均數的距離的平均數,反映一個數據集的離散程度。一個較大的標準差,代表偏差較大,風險也較大,反之則相反;(3)最大值、最小值:表示A產品下一年收入的變動區間;(4)編制累積頻率分布圖。
為了便于數據統計,我們將已產生的5000組數據劃分為40個段位,引用其最小值、最大值,計算得出相應的步長(STEP)為432(即(18920-2070)/39=432),由此得到了分組數值。利用EXCEL的FREQUENCY函數得到了5000組數據在各分段區域出現的頻次,進而求得了頻率及累積頻率。下表為部分分組數據的截圖:
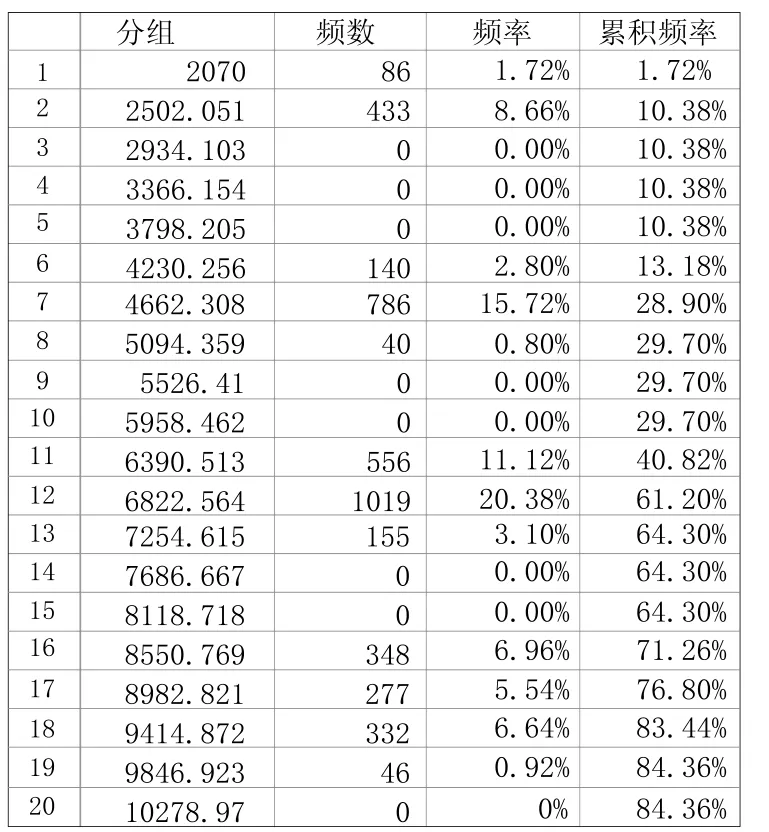
圖2
選取“分組”、“累積頻率”作為圖表數據,以散點圖方式編制成累積頻率分布圖。
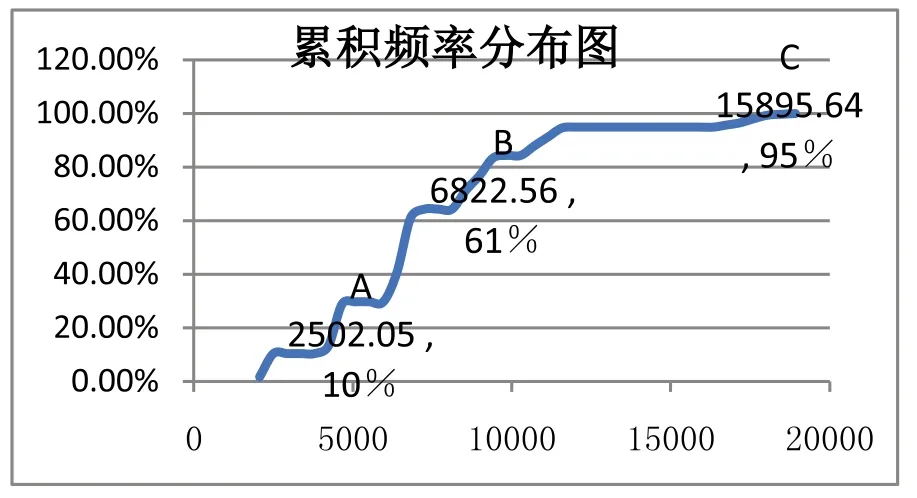
圖3
由圖3可知,該企業A產品下一年收入在2500萬元以下的概率為10%,收入在6800萬元以下的概率超過50%,收入超過15900萬元的概率幾乎很小。
當然,企業可以結合自身實際情況,任意設置關鍵點指標,如通過企業資金需求情況、測算產品線的保本點、各種互補產品的利潤比較等來反推產品收入是否能達到企業需求的概率,為企業投資融資決策提供高效的財務支撐。
4 運用蒙特卡羅模擬時需注意的事項
該模擬方法可以模擬多元素風險因素變化對結果的影響,但其也有一定的局限性。其要求的數據量較多,且模擬的數據變量要求是相互獨立的,如果必須輸入一個模式中的隨機數并不像設想的那樣是隨機數, 而卻構成一些微妙的非隨機模式, 那么整個的模擬(及其預測結果)都可能是錯的。雷曼企業所用風險模型中大量使用模擬技術,模型假設與現實嚴重割裂,加之模型過度包裝導致信息嚴重不對稱被認為是其倒閉的因素之一。因此,在財務預測中對一些復雜重大的問題,想要達到較高的模擬精度除了需進行較多的模擬次數外,仍不可忽視與現實狀況的匹配度原則。
[1] 李志偉.風險型決策的蒙特卡羅模擬——風險項目投資決策案例分析[A].當代管理會計新發展——第五屆會計與財務問題國際研討會論文集(下)[C].2005.
[2] Broadie P.Glasserman P Monte Carlo methods for securities pricing.1997.
[3] 王克強,劉洪衛,劉紅梅.Excel在工程技術經濟學中的應用[M].2005.
[4] 徐全華,王華,梁權熙.會計穩健性、財務困境與公司風險轉移[A].2011學術年會論文集[C].中國會計學會,2011.

