云計算中數據資源的安全加密機制

程玉柱 胡伏湘

（長沙民政職業技術學院軟件學院，湖南長沙410004）

隨著通信技術和云計算技術的高速發展，人們在互聯網上的數據共享和訪問日益頻繁，數據的安全性面臨著更為嚴峻的挑戰，安全問題已成為阻礙云計算發展的關鍵因素，也是云計算得以普及的前提。概括地說，云計算是將大量的、可規模化的IT資源作為一種服務通過因特網提供給多個外部用戶。在云計算這種新的服務模式下，數據提供者和數據訪問者不再是簡單的一對一關系，數據提供者將數據存放在第三方云計算服務提供商提供的數據存儲中心，數據訪問者通過云計算服務提供商提供的多種開發接口而訪問數據提供者發布的重要數據。然而，如云安全聯盟白皮書所指出的那樣，存儲在云服務端的數據很可能被非可信的云計算服務提供商或非法用戶竊取。因此，針對當前云計算中數據資源所面臨的威脅，如何利用有效的安全加密機制來加強數據的安全性、防止數據泄露和加強隱私保護是云安全的一個關鍵問題。

1.數據加密的基本原理

1.1 數據加密的基本概念和一般原理

數據加密的基本過程就是對原來為明文的文件或數據按某種算法進行處理，使其成為不可讀的一段代碼，通常稱為“密文”。其只能在輸入相應的密鑰之后才能顯示出本來內容，通過這樣的途徑來達到保護數據不被非法竊取、閱讀的目的。該過程的逆過程為解密，即將該編碼信息轉化為其原來數據的過程[1]。

一個典型的數據加密模型如圖1所示：

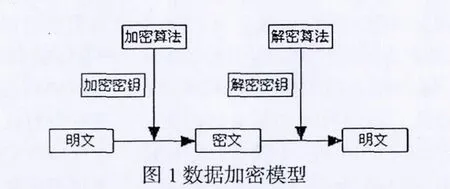
一個安全的加密技術應該滿足五個基本要求：一是必須提供高強度的安全性。二是具有高強度的復雜性，使得破譯的開銷超過可能獲得的利益，同時又便于理解、掌握和推廣應用。三是安全性應不依賴于算法的保密，其加密的安全性僅以加密密鑰的保密為基礎。四是必須適用于不同的用戶和不同的場合，加解密變換必須對所有密鑰均有效。五是理想的加密算法應該是對系統性能幾乎沒有負面的影響。

1.2 加密算法分類

從密鑰的特點來分類，加密算法可以分為對稱密碼算法和非對稱密碼算法[1]。對稱密碼算法又稱為傳統密碼算法，其特點是在加密與解密過程中使用相同的密鑰，而與之相對應的是非對稱密碼算法。顧名思義，非對稱密碼算法的加密密鑰不同于解密密鑰，加密密鑰（公鑰）公之于眾，而解密密鑰（私鑰）卻只有解密人自己知道。日常生活中，非對稱密碼算法又稱為公鑰密碼算法。

1.2.1 對稱密碼體制

對稱密碼體制是指加密與解密密鑰相同或等價，而且通信雙方必須都要獲得這把密鑰，并保持其機密性。當給對方發信息時，用自己的加密密鑰進行加密，而在接收方收到數據后，用對方所給的密鑰進行解密。因為加解密密鑰相同，需要通信的雙方必須選擇和保存他們共同的密鑰，各方必須相信對方不會將密鑰泄密出去，這樣就可以實現數據的機密性和完整性。由于安全強度高，加密速度快，對稱加密技術是最常用的加密技術，典型的對稱密碼算法有 DES、AES、IDEA等。

DES（Data Encryption Algorithm）數據加密標準，是一個對稱的分組密碼算法。加密前將明文分成固定長度的組，用同一密鑰對每一塊加密，輸出也是固定長度的密文，加密過程使用64位密鑰來對64位數據塊進行加密，并對64位數據塊進行16輪編碼。64位一組的明文從算法的一端輸入，64位密文從另一端輸出。DES加密數據速度快、效率高，被廣泛用于大量數據的加密。

IDEA（International Data Encryption Algorithm）是國際數據加密算法，它使用128位密鑰，每次加密一個64位的數據塊。IDEA算法的安全性相對DES算法有很大的提高，其密鑰是128位，而且它比DES在軟件實現上快得多。

AES（Advanced Encryption Standard）即高級數據加密標準，是一個迭代的對稱密鑰加密標準，是基于排列和置換運算，現在已經成為新一代的數據加密標準。AES加密的分組長度都是可變的，其密鑰可以是128、192和256位密鑰，一般較常用的密鑰長度是128位，并且可以根據自己的需要選擇分組的長度和加密的輪數來保證數據的安全。AES加密與DES相比有很強的保密強度，安全級別較高，且能經受住時間的檢驗和攻擊。密鑰的長度及速度都高于DES，且資源的消耗較低，但是同樣為對稱密鑰，密鑰必須通過安全的途徑傳送，密鑰管理困難。

1.2.2 非對稱密碼體制

非對稱密碼體制要求密鑰成對使用，加密和解密分別用兩個密鑰來實現。每個用戶都有一對選定的密鑰，一個可以公開，即公共密鑰，用于加密；另一個由用戶安全擁有，即秘密密鑰，用于解密，非法用戶根據公開的加密密鑰在計算上并不能算出解密密鑰。該技術就是針對對稱密碼體制的缺陷被提出來的[2]。如果一個人選擇并公布了他的公鑰，另外任何人都可以用這一公鑰來加密傳送給那個人的消息。私鑰是秘密保存的，只有私鑰的所有者才能利用私鑰對密文進行解密。非對稱密碼系統可提供以下功能：

（1）機密性（Confidentiality）：保證非授權人員不能非法獲取信息，通過數據加密來實現。

（2）確認（Authentication）：保證對方屬于所聲稱的實體，通過數字簽名來實現。

（3）數據完整性（Dataintegrity）：保證信息內容不被篡改，入侵者不可能用假消息代替合法消息，通過數字簽名來實現。

典型的公鑰密碼算法有RSA和ECC。RSA是當前最著名的、應用最廣泛的公鑰算法，安全性基于大整數素因子分解問題的困難性，它是一種分組加密算法，該算法原理簡單，易于使用[3]。ECC（Elliptic Curve Cryptosystem）即橢圓曲線密碼體制，是建立在求橢圓曲線離散對數困難基礎上的，它的安全性依賴于橢圓曲線離散對數問題的安全性，是目前最流行的一種公開密鑰密碼體制。ECC與RSA方法相比，它的安全性更高，只需要160位的密鑰就可以達到1024位RSA算法提供的安全等級，有更好的加密強度，計算量小且處理速度快。

2.云計算環境下數據資源的加密技術分析

在云計算環境中，針對用戶數據資源所面臨的安全威脅，目前所采用的最基本、最核心的技術是數據加密技術，其利用密碼學里的相關技術對信息進行替換或者移位，實現信息隱藏，從而保護信息的安全。然而，隨著近年來云計算技術的高速發展，用戶在互聯網上的數據共享日益頻繁，傳統的加密體制和方法已經不能適應新的網絡環境下層出不窮的應用需求。云計算中數據資源安全加密體制遇到了一些新的挑戰，同時也引起了研究界的廣泛關注。

2.1 對稱密碼體制

數據擁有者首先與數據訪問者協商一對加、解密密鑰，然后利用加密密鑰對數據進行加密，數據訪問者則從數據擁有者或密鑰管理中心KCC處獲取相應解密密鑰（對稱密碼體制中，解密密鑰=加密密鑰）。該方案存在的兩個主要問題是：第一，每一個數據訪問者均需要與數據擁有者協商一對密鑰，當訪問用戶很多時，需要協商的密鑰數量將會很龐大；第二，在不安全的網絡環境中，密鑰將通過什么安全通道進行協商或分發？

2.2 非對稱密碼體制

基于對稱密碼體制下密鑰的協商和分發難題，非對稱密鑰體制用公鑰加密，而用私鑰來解密，從而實現了加密密鑰和解密密鑰的分離，但該體制存在兩個典型問題：第一、如何確認公鑰的正確性？目前確認加密用公鑰的正確性一般是通過設立一個可信第三方（即證書中心CA）來對公鑰進行認證，在云計算環境下，用戶數量可能會非常龐大，這就對CA的安全性和管理負荷帶來了一定的挑戰。第二、當數據擁有者希望共享自己的數據時，需要獲得每一個訪問用戶的公鑰來對數據進行加密，而訪問用戶則憑借自己的私鑰對密文進行解密。這種方式對數據擁有者的共享帶來了很大的操作負擔，每增加一個授權訪問用戶，就需要去CA獲得該訪問用戶的公鑰，對共享數據加密后再進行發布。

2.3 基于身份的加密體制[4]

針對非對稱密碼體制下公鑰正確性證明需要提供一個CA中心的問題，在基于身份的加密體制下，采用用戶的身份信息作為其公鑰，從而避免了額外設立CA中心的負擔。也就是說，公鑰真實性問題和證書管理問題在基于身份加密的系統中就不再需要。但基于身份的加密體制仍存在的問題是，如果數據擁有者希望所共享的數據可以為多個授權用戶訪問，則同樣需要分別采用每個訪問用戶的身份信息作為公鑰來對數據進行加密。

2.4 基于屬性的加密體制

基于用戶的身份信息唯一，但其屬性可能會有共性的特點，Sahai和Waters在2005年歐洲密碼年會上發表了《模糊基于身份加密方案》一文[5]，首次提出了基于屬性加密的概念。與基于身份的加密體制中采用用戶的唯一身份信息作為公鑰不同，基于屬性的加密體制采用用戶的屬性集合作為公鑰來對數據進行加密，如果一個訪問用戶能夠解密一個密文，當且僅當該用戶的屬性集合和密文的屬性集合共有屬性的數量達到門限要求。在該加密體制中，引入了包含與、或、非，以及門限能力的訪問樹結構，使得密文可以被多個用戶共享。

舉一個例子說明：假設系統中門限為3，因此只有用戶的屬性集合中至少有3個屬性與密文屬性集合相同，用戶才能解密。設a,b,...h表示系統中的屬性，若系統中有三個用戶分別為:A(a,b,c,d,e)，B(b,c,e,f)，C(a,d,g)。現有一個密文，其密文的屬性集合為(b,c,d,f)。因為系統的門限是3，這就要求解密用戶的屬性集合至少含(b,c,d,f)中三個或三個以上的屬性。從A,B,C三個用戶的屬性集合可以看出A和B滿足條件，他們的屬性集合滿足了解密條件，能夠解密密文。而用戶C屬性集合不滿足要求，因此不能解密。

因為基于屬性加密方案中加密和解密具有動態、靈活的特性，能夠實現對系統中用戶的解密能力和密文的保護方面的細粒度控制。近幾年來，基于屬性加密成為公鑰密碼學的研究熱點[6-8]。

3.云計算環境下數據加密的發展趨勢

綜合對目前主流的加密方案進行分析，對稱密碼體制在加解密速度上占有一定的優勢，但在云計算環境下，其密鑰管理和分發的障礙更為突出。非對稱密碼體制一定程度上解決了對稱密碼體制在密鑰管理和分發的難題，但在公鑰管理和分發上需要設立一個公鑰認證中心，在云計算環境下該認證中心很容易成為黑客重點攻擊的目標，且一旦其被攻破，則用戶數據安全性不再得到保證。基于身份的加密體制可以不再需要認證中心，但其仍然存在的問題是用戶希望共享數據時，需要獲取所有訪問用戶的身份信息來對數據進行加密，其代價比較大。而基于屬性的加密體制從原理上較適合云計算環境下的針對多用戶的數據共享問題，在很多應用場景下不再需要認證中心來管理和分發密鑰，而且針對多訪問用戶，可以用他們的共有屬性集來設計加密方案，實現了對用戶解密密文的細粒度控制。然而據我們所知，到目前為止，基于屬性的加密體制在某些擴展應用場景中還存在一些問題，比如針對所有屬性情況下的訪問樹設計是否可行？能否在不設立認證中心的前提下，處理新增用戶訪問的要求？如何處理在云計算環境下，基于屬性加密體制的用戶單點登錄問題？

4.結束語

數據作為一種資源，其安全的重要性顯而易見，業已成為云計算技術發展的關鍵與難點。而加密則是目前保障數據安全的重要措施。隨著云計算技術的發展，對數據加密技術提出了越來越高的要求，各種加密算法陸續被提出、應用、否定和改進。目前來看，由于不同體制的加密算法各有所長，所以在今后相當長的一段時期內，各類加密體制將會共同發展。而基于屬性的加密算法在近年得到廣泛的關注，不僅僅是因為其在理論設計上的復雜性，更因為基于屬性密碼以及相關研究的巨大應用價值。基于屬性的加密算法在把對身份的控制和認證擴充為對用戶擁有的屬性集合的認證，提供了豐富的控制手段。通過門限，與門和或門等控制單元構造出可以適應多種情況的訪問控制結構。但是現有的一些基于屬性的加密算法以及相關的方案還存在一些需要改進和關注的問題，有待研究的繼續深入。

[1]吳世忠.應用密碼學－協議、算法與C源程序[M],北京:機械工業出版社,2000.

[2]W Diffie,M E Hellman.New directions in cryptography[J],IEEE Transon Inf.Theory,1976,22(6):644-654.

[3]R L Rivest,A Shamir,L Adleman.A method for obtaining digital signatures and public key cryptosystem[C].Comm.ACM.1978.21:120-126.

[4]D Boneh,M K Franklin.Identity-based encryption from the weil pairing[C].CRYPTO,2001,213-229.

[5]Sahai A,Waters B.Fuzzy identity based encryption[C].Advances in Cryptology(EUROCRYPT 2005).Lecture Notes in Computer Science(3494),Berlin:Springer-Verlag,2005.457-473.

[6]Bethencourt J,Sahai A,Waters B.Ciphertext-policy attribute-based encryption[C].Proceedings of IEEE Symposium on Security and Privacy,2007.321-334.

[7]Attrapadung N,Imai H.Dual-Policy Attribute Based Encryption[C].Proceedings of Applied Cryptography and Network Security.Lecture Notesin Computer Science(5536),Berlin:Springer-Verlag,2009.168-185.

[8]Guo Z Z,Li M C,Cui Y R,Fan X X.Dynamic multi-attribute based encryption[J],JDCTA:International Journal of Digital Content Technology and its Applications,2011,Vol.5:281-289.