小型電子產品流水化生產線設計模型的研究

潘繼承，姜雪松*，李東宸

（1.東北林業大學工程技術學院，哈爾濱150040;2.東北林業大學機電工程學院，哈爾濱 150040）

流水線［1］質量的高低直接影響著產品的質量和生產效率，每年因為產線不平衡問題而導致流水線停產檢修，嚴重影響了企業的效益［2］。據不完全統計，僅2009年珠三角地區小型電子產品（Small Size Electronic Products，簡稱SSEP）制造企業因為產線不平衡問題，導致產品出現質量問題，產線停產，甚至企業倒閉，造成直接經濟損失達幾十億元人民幣。

采用流水線方式生產的企業，流水線平衡［3］成為一個重要的生產管理問題。流水線平衡問題自1955年Salveson首次提出以來，許多研究人員對此展開了大量的研究，主要可分為精確算法和近似算法兩大類，并在不同程度上取得了可喜的成果［4］。

但是流水線平衡問題的根源還是源于流水線最初的設計，只有設計出一條好的生產線，在此基礎上才能進行進一步的優化［5－7］。本文將針對HX—118—2型號收音機，結合SSEP流水線本身的特點，在了解收音機內部電子元器件構造的基礎之上，通過分析電子元器件裝配的優先等級，依據生產計劃，得出合理的生產節拍，建立流水線工序分配的運籌學模型，使流水線的各工序之間時間差最小。

1 HX－118－2型號收音機資料收集

收音機的原始資料包括內部電子元器件的組成，需要根據其特點對其分類，見表1。除此之外，同一種類別的電子元器件，也需要根據其自身的不同屬性，依據不同的標準，見表2，進行分析和編號分類，見表3。同時，一條流水線的設計還需要產品零件圖、裝配圖、生產工具、產品質量驗收標準等。

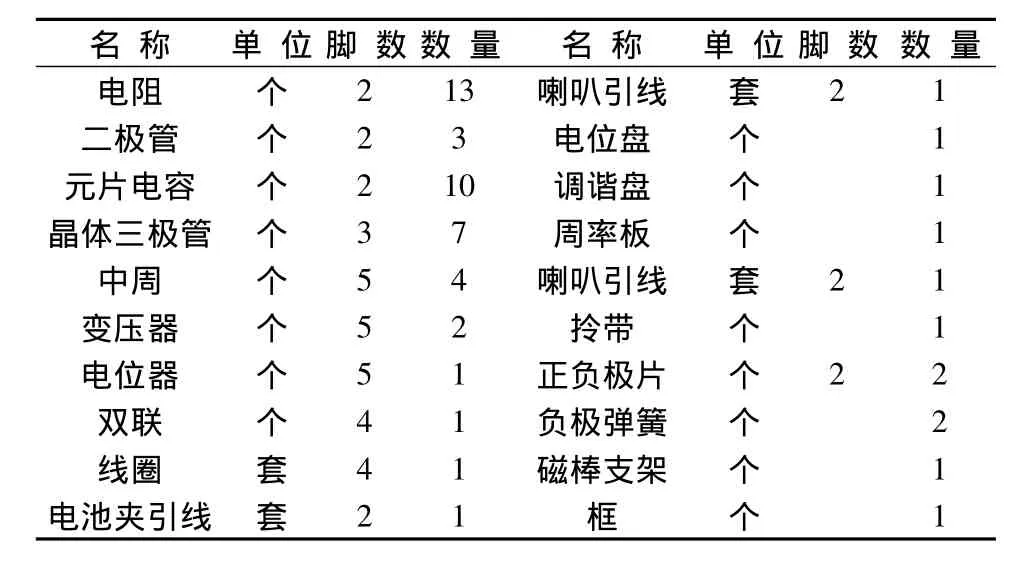
表1 收音機電子元器件表Tab.1 Electronic components of a radio

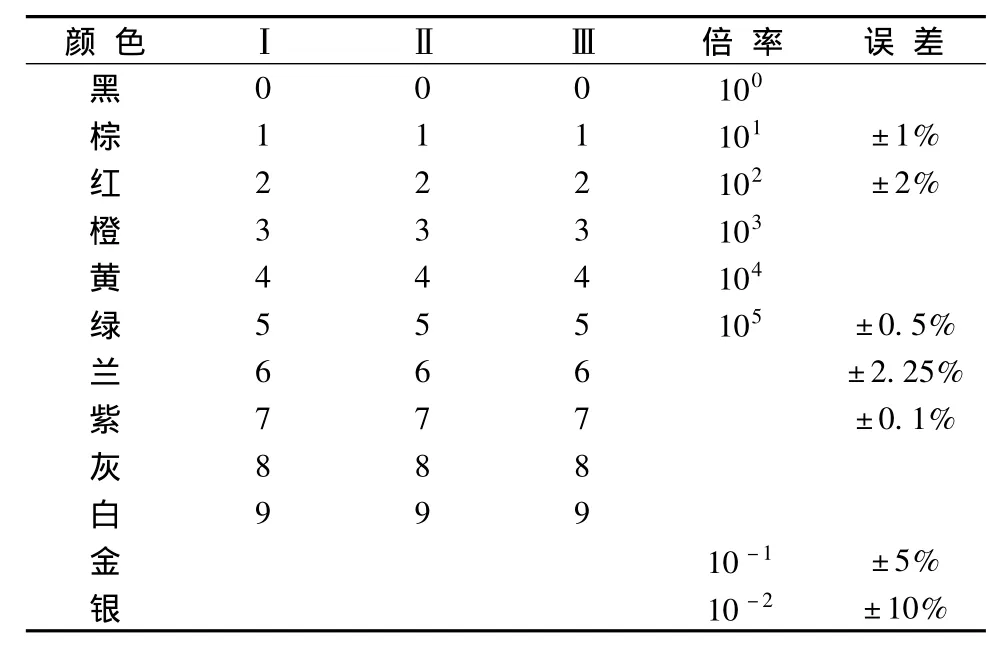
表2 顏色阻值對照表Tab.2 The color of different electric resistivity

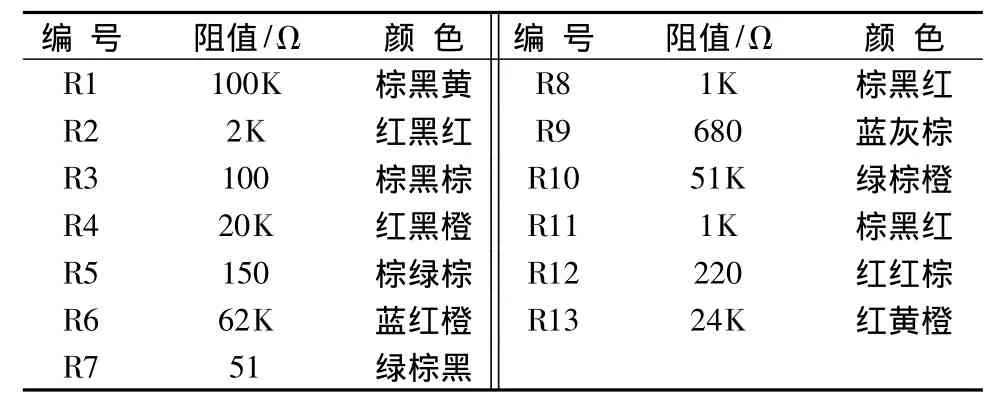
表3 電阻編號表Tab.3 The numbering of different electronic resistivity

2 數據分析與建立模型

2.1 確定流水線的節拍

節拍的長短由計劃期的產量和計劃其有效工作時間的長短來決定［8］。計劃期產品產量包括計劃期出產量（合格品）、預計廢品量和儲備量的變化量。本文計劃收音機流水線的計劃日產量為900件，每天工作8 h，采用兩班制生產，每班停休20 min，計劃廢品率為2%，則:

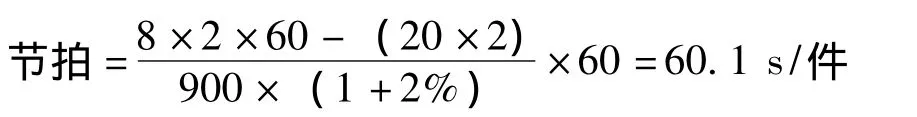
2.2 確定裝配元件的優先等級

參照收音機的裝配說明書，分析產品內部電子元器件的構造，根據元件尺寸大小和其他裝配準則，確定元器件的裝配優先級。電子元件編號見表4，裝配優先等級如圖1所示。

表4 電子元件編號表Tab.4 The numbering of different electronic components

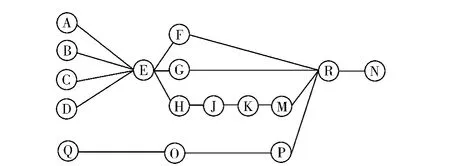
圖1 裝配優先圖Fig.1 The priority of assembling

2.3 計算生產節拍

在產品實際投入生產之前，我們無法知道每個步驟所需要的時間，就需要利用模特法［9］預先估計出裝配每一個電子元件所需的時間作為參考。各元件裝配時間見表5。

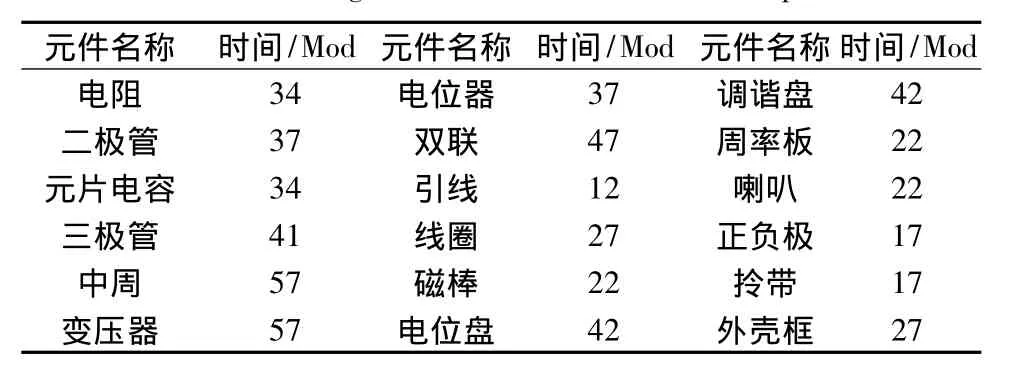
表5 裝配時間表Tab.5 Assembling time of different electronic components

由于模特法估計出來的時間在實際中根本無法達到，必須考慮寬放，設寬放率為30%，即參考時間=估算時間×1.3。前面確定的生產節拍為60.1 s，所以單個大工序的時間約為60/0.129=465Mod。依此時間對個小工序進行線性組合，建立線性規劃的模型，合成單個大工序。

2.4 模型的建立

運籌學模型一般包含三個組成要素:

（1）決策變量，指決策者為實現規劃目標采取的方案措施，是問題中要確定的未知量。

（2）目標函數，指問題要達到目的的要求，表示為決策變量的函數。

（3）約束條件，指決策變量取值時受到的各種可利用資源的限制，表示為含決策變量的等式或不等式［10］。

在本文中，需將不同的電子元器件分配到不同的工序去完成，每個工序所需要完成的電子元器件的個數為決策變量，設xiyi為第yi個工序所需要完成的第i個元件的個數;ai為完成一個i元件裝配所需要的時間，ai為已知量;yi為進行第i種元件裝配所在的工序數。

首先需要確定目標函數，每個工序的時間越小越好，但是完成原件裝配的總時間加在一起是不變的，即工序越多每個工序的時間就越小，但是工序過多會需要較多的工人，我們要求的是在有限的工序里，通過合理的分配，使在所有工序中時間最長的那個工序的時間越短越好，這樣完成單個產品的時間就會縮短。設T為單個工序的時間，則目標函數為

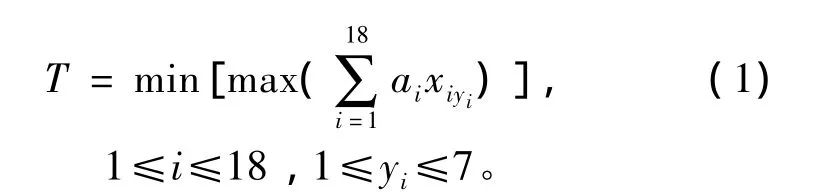
對于單個大工序，它的時間大約為465Mod，對此我們進行約束，它的所有單個大工序時間都不能超過465Mod，即

元件的裝配是有先后順序的，如果裝配的先后順序混亂將造成最后有的元件由于大小或其它問題無法裝配。由于同種電子元件的個數不止一個，所以可能將分配在多個工序中進行裝配，所以設yim表示集max{yi}，即yi的最大值，則由優先圖可得y1≤y5;y2≤y5;y3≤y5;y4≤y5;y5≤y6;y5≤y7;y5≤y8;y8≤y9;y9≤y10;y10≤y11;y11≤y12;y12≤y13;y11≤y12;y13≤y18;y6≤y18;y7≤y18;y17≤y15;y15≤y16;y16≤y18;y14≤y18;y15≤y16。

在很多實際問題中，全部或部分變量的取值必須是整數，如人或機器設備等不可分割。在本文中，電子元件是不可分割的，所以個數必須取整數，工序之間是相互獨立的，所以也都必須取整數，即i、yi、xiyi為整數。

2.5 模型的求解

目標函數和約束條件共同構成了生產排產的模型，可以進行人工計算求解，也可以利用計算機軟件求解。人工計算求解計算量是比較大的，計算準確度和精度不夠好，但求解思路很明晰簡單;利用計算機軟件求解，如Lingo，求出的解準確度和精度比較好，但需要有較高的軟件應用水平［11］。

人工計算法:約束條件不等式限定了裝配的先后順序，基于優先圖，可先初步劃分各個工序所分配的裝配元件組合，只要時間是在465Mod以內都是合理的，然后從所有工序時間中找出時間最大的工序，將其所要裝配的元件中的一部分分配到工序時間較小的工序中，但分配的元件裝配順序必須要滿足優先圖。然后再找出工序時間最長的工序，再進行拆分、分配，循環的進行，直至各工序時間相差不多，這樣元件的分配就排出來了，這樣得出的結果一直在向最優逼近。基于Lingo軟件的求解:使用Lingo軟件求解運籌問題可以分為兩個步驟來完成:

（1）根據實際問題，建立模型。

（2）利用Lingo來求解模型，主要是把模型轉移成計算機語言，借助于計算機來求解，所以要求必須能夠熟練地進行模型編譯。

本文將通過人工計算法給出求解的結果，得到最優大工序組合見表6。

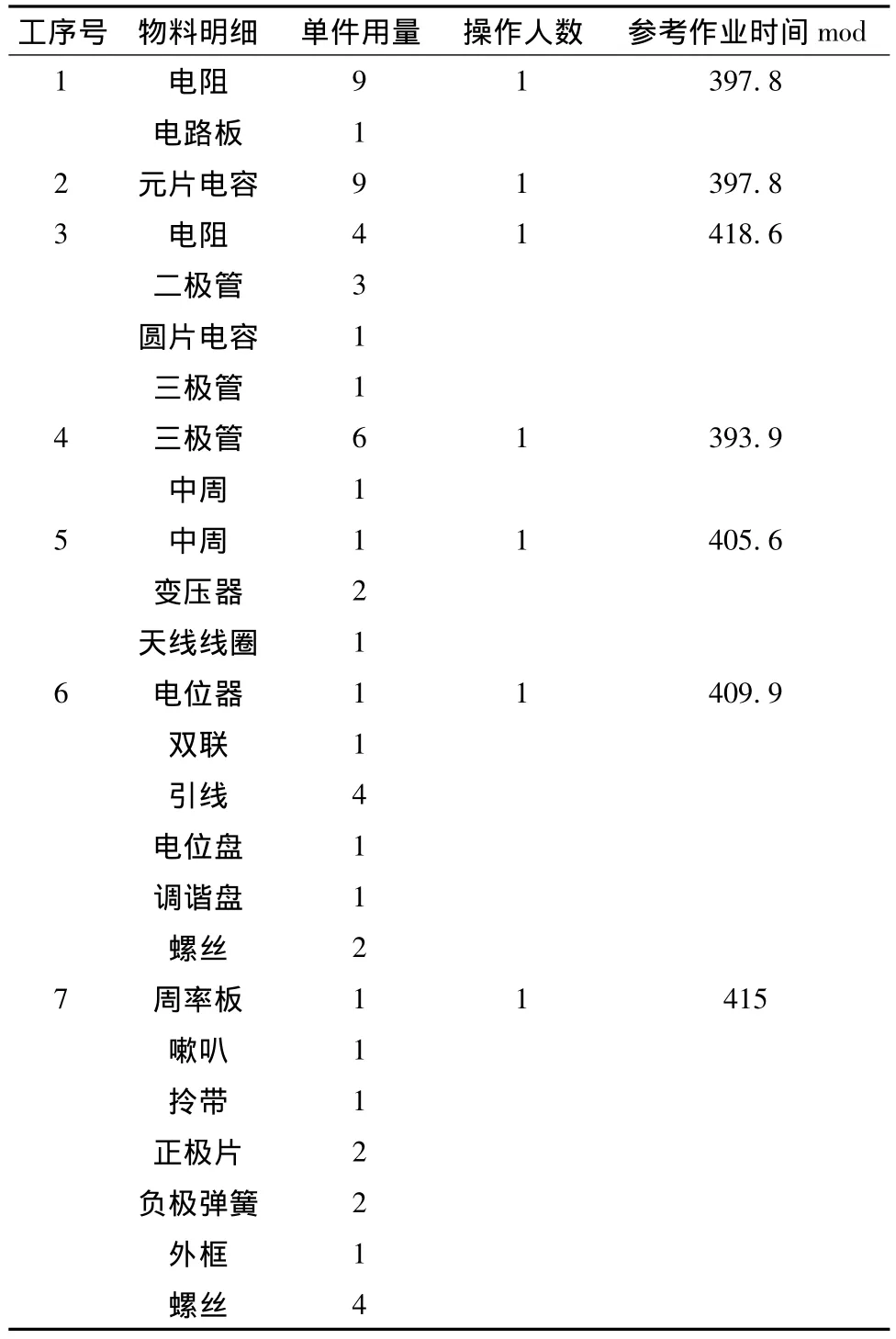
表6 組裝順序表Tab.6 Assembling order

3 模型的檢驗

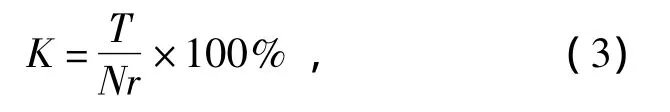
式中:K為流水線負荷系數;T為流水線各工序作業時間之和;N為平衡后流水線實際工作地數;r為節拍。本文中流水線負荷系數K為87.2%。流水線損失時間;

本文中計算出損失時間S為53.72 s。流水線時間損失系數

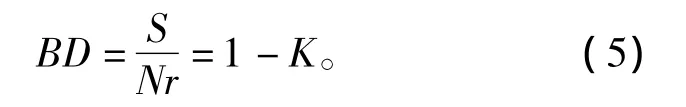
流水線負荷系數:

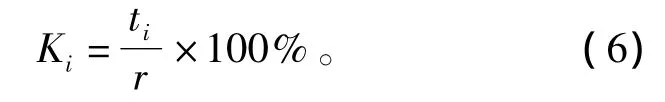
流水線負荷系數決定了流水線作業的連續程度，一般機器工作流水線的負荷系數不應低于75%，以手工為主的裝配線限負荷系數不應低于85%。本文中計算出K1=0.86，K2=0.86，K3=0.90，K4=0.85，K5=0.87，K6=0.88，K7=0.89。計算出的Ki均在85%以上，所以流水線作業的連續程度較好。

本文中計算出BD為12.8%。為了評估各工作地效率，還要計算出各個工作地的負荷系數。設第i個工作地作業時間為ti，則該工作地負荷系數Ki為:

4 結論

本文針對SSEP流水線的現狀，從產線優化設計角度對產線進行研究，以HX－118－2型號收音機為例，將運籌學模型應用到SSEP流水線的設計之中，得出電子元器件裝配的分配工序，使工序間的時間差達到最小，從優化設計角度使流水線獲得較高的平衡率。流水線設計中的運籌學模型建立及多元方程的求解方法，為國內現有的以手工操作為主的SSEP流水線設計，提供了理論方法和實踐依據。

】

［1］易樹平，郭 伏.基礎工業工程［M］.北京:機械工業出版社，2007.

［2］羅杰·G施羅德.運作管理［M］.韓伯棠.北京:北京大學出版社，2002.

［3］齊二石.現代工業工程與管理［M］.天津:天津大學出版社，2007.

［4］孫建華，高廣章，蔣志強.生產線平衡的手段與方法研究［J］.現代生產與管理技術，2004，21（4）:34 －36.

［5］王 晶，葛安華.液晶顯示器裝配生產線平衡與優化研究［J］.森林工程，2009，25（1）:28 －32.

［6］包才慶.單一對象流水線的組織設計和應用［J］.林業機械與木工設備，2012，（10）:4055 －4056.

［7］劉家發.新型雙齒條差動扎鉤裝置的應用［J］.林業機械與木工設備，1996，24（4）:29 －30.

［8］甘 凱，李隨成，王 銳.某電器公司裝配流水線平衡研究［J］.人類工效學，2006，12（3）:36 －38.

［9］郭 伏.模特法在生產線能力平整中的應用［J］.東北大學學報，2003，1（5）:31 －32.

［10］胡運權.運籌學基礎及應用［M］.北京:高等教育出版社，2004.

［11］萬義國，游小青.優化建模軟件Lingo在運籌學中的應用［J］.山西建筑，2007，33（15）:367 －368.