多服務窗等待制M/M/n排隊模型

付馨雨，羅國旺

(重慶師范大學數學學院，重慶 400047)

在日常生活中，經常可以看到許多排隊模型同時具有可變輸入率與可變服務率的特性，如銀行儲蓄排隊、大型超市付款臺排隊等均屬此類排隊模型。即當服務窗口前排隊顧客較多時，顧客會猶豫是否加入系統排隊等待;而服務人員為了避免損失顧客，就會適當地提高服務速度。關于具有不耐煩顧客的排隊模型已有很多學者進行了研究，文獻［1－5］研究了具有不耐煩顧客的M/M/1及M/M/n排隊模型。然而，有關將可變輸入率和可變服務率與具有不耐煩顧客相結合的M/M/n排隊模型還未得到學者關注。本文研究了輸入率可變且具有兩類服務率及不耐煩顧客的M/M/n排隊模型。

1 模型假設

為了方便對多服務窗等待制M/M/n排隊模型的研究，做如下假設:

1)系統中有n個服務窗口，容量無限。

2)顧客到達系統的時間間隔服從參數為λ的指數分布。

3)假定顧客到達系統后加入隊列的概率為αk(0＜αk＜1)，即 αk依賴于隊長 k。當 k→∞時，αk→0，此時的輸入率 λk=αkλ。在此僅討論

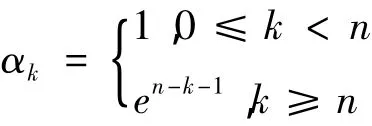
4)多個服務臺間相互獨立，當系統中排隊長度超過n時，服務窗用快速服務率μ2，反之則用慢速服務率μ1。

5)服務時間與顧客到達的時間相互獨立，且系統中的顧客排成一個隊。

6)記βk為具有不耐煩顧客離開的概率，k表示等待隊長(此時系統中已有n+k個顧客)。隊伍中不耐煩顧客離開隊伍的強度δ≥0。

2 數學模型

根據上面的假設不難得到以下定理:

定理1 令X(t)表示時刻t系統中的顧客數(隊長)，則{X(t)，t≥0}是以狀態空間為 E={0，1，2，3，…}且

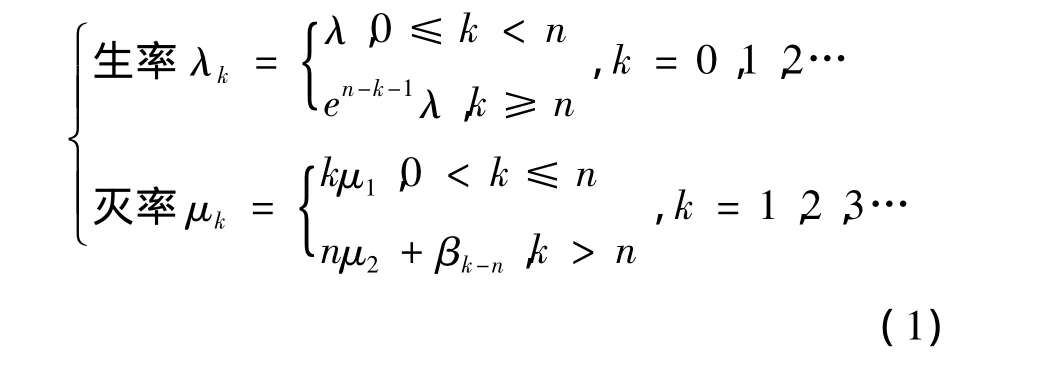
的生滅過程。

證明 略，可參見文獻［3－4］。

畫出系統狀態流圖，見圖1。

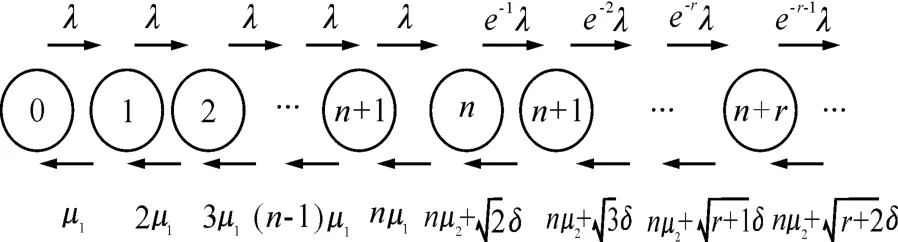
圖1 多服務窗等待制M/M/n模型的狀態流圖

3 平穩分布

由以上的數學模型得到模型的平穩分布，即定理2。

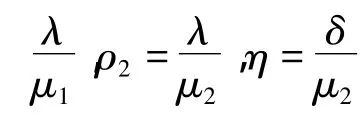
證明 由圖1可列出平衡條件下的k氏代數方程，并求出其平穩分布，解析表達式為:

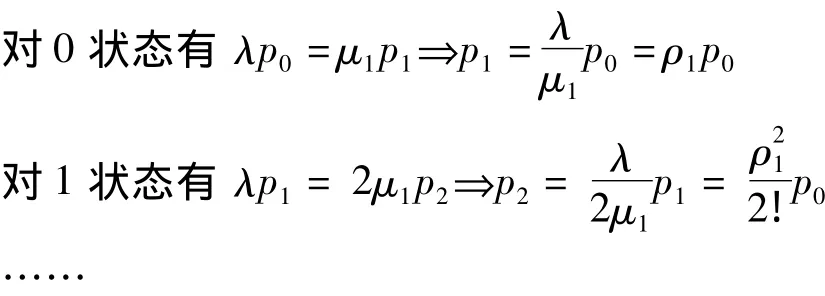
4 主要指標

根據平穩分布，得到如下主要數學指標。

1)顧客排隊等待的概率。由式(2)可得顧客排隊等待的概率為

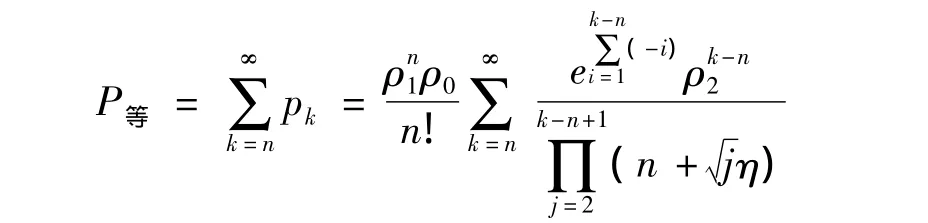
2)平均等待隊長(系統內排隊等待顧客數的均值)。首先等待隊長lq有如下分布列:

3)平均繁忙中的服務窗個數。注意到繁忙中的服務窗個數Y有如下分布列:

4)系統的平均隊長(系統內顧客數的均值)為

5)單位時間內平均離開隊列的不耐煩顧客數為

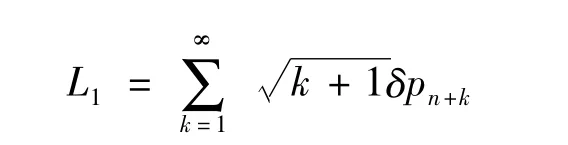
6)絕對通過能力(單位時間內被服務完的顧客均值)為

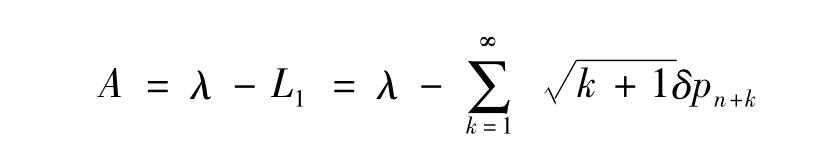
7)相對通過能力為

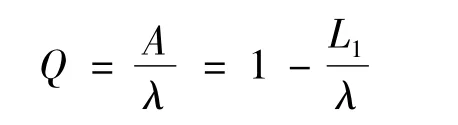
8)由little公式得顧客在系統中的平均逗留時間和平均等待時間:

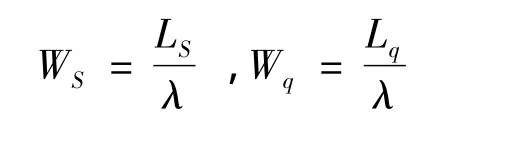
5 結束語

本文研究了可變輸入率且具有兩類服務率及不耐煩顧客的M/M/n排隊模型，充分考慮了輸入率、服務率以及不耐煩顧客與系統中隊長的關系，并獲得了該模型的平穩分布和主要指標。該模型可以幫助解決銀行、超市、商場等服務行業中的不同輸入率、不同服務率以及不耐煩顧客問題，從而將文獻［2］推廣到更為一般的情形，使其更具有普遍性，為實際運用提供了一定的理論基礎。

［1］陸傳賚.排隊輪［M］.北京:北京郵電大學出版社，2009.

［2］李煥.具有可變輸入率和不耐煩顧客M/M/n的排隊模型［J］.重慶師范大學學報:自然科學版，2011(3):49 －52..

［3］孫榮恒，李建平.排隊論基礎［M］.北京:科學出版社，2002.

［4］孫榮恒.隨機過程及其應用［M］.北京:清華大學出版社，2004.

［5］臺文志，高世澤.一類具有可變輸入率的M/M/1排隊模型［J］.重慶師范大學學報:自然科學版，2009，26(1):69－72.

［6］劉次華.隨機過程及其應用［M］.北京:高等教育出版社，2004.

［7］唐應輝，唐小我.排隊論基礎與分析技術［M］.北京:科學出版社，2006.