基于小波能量的簇絨地毯跳紗疵點的檢測方法

翟琳琳，陳廣鋒

(東華大學紡織裝備教育部工程研究中心，上海201620)

簇絨地毯的外觀檢測是對其進行質量控制的重要項目之一［1］。長期以來，對于簇絨地毯中的疵點都是通過人工檢測，檢驗人員按照個人經驗對地毯等級做出評定，這種方法受檢驗人員的主觀因素影響較大［2］，效率低、漏檢率高，且勞動強度大，難以得到準確的檢驗結果。基于機器視覺的疵點檢測技術具有快速、準確和低成本等特點，可以有效解決地毯疵點的在線檢測問題。

簇絨地毯的疵點種類很多，有破損、臟污、跳紗、斷紗等，均呈現復雜的外觀形態。疵點可以產生于生產過程中的任何階段，而且地毯紗線較粗，紋理粗糙，地毯的顏色和式樣也多種多樣，這都為疵點檢測帶來一定的難度。目前，針對布匹表面疵點檢測的相關理論研究很多，檢測技術也已經比較成熟，比如紋理分析方法、傅立葉變換法等，但由于簇絨地毯上疵點的復雜性，針對于地毯上疵點檢測的研究還很少。筆者針對簇絨地毯的跳紗類疵點進行了研究，并提出一種基于小波能量的疵點檢測方法，有效地實現簇絨地毯上此類疵點的檢測。圖像疵點檢測流程為:1)利用圖像采集系統對地毯圖像進行采集;2)對采集到的圖像進行預處理;3)對地毯圖像進行判斷，判斷其是否存在疵點;4)對存在疵點的圖像進行疵點分割，提取疵點信息并在源圖像中進行定位。

1 簇絨地毯圖像預處理

采集到的地毯圖像存在著噪聲信號，需要對圖像進行處理以修正灰度和校正畸變。圖像預處理的主要目的是消除地毯圖像中的正常紋理，增強疵點圖像信息的可檢測性和最大限度地簡化數據［3］，從而改進圖像分割和疵點識別的可靠性。本文使用空間域濾波的方法對簇絨地毯上的跳紗疵點圖像進行濾波處理，以達到平滑正常紋理，突出疵點信息的目的。

空間濾波器是由一個鄰域和對該鄰域所包圍的圖像像素執行的預定義操作組成的，其濾波的過程為:對圖像中的每一點(x，y)，重復下面的操作:1)對預先定義的以(x，y)為中心的鄰域內的像素進行運算;2)將1)中運算的結果作為(x，y)點的新響應。

如果鄰域中的像素計算為線性運算，則又稱為線性空間域濾波，否則稱為非線性空間域濾波。在圖像中的任意一點(x，y)，濾波器的響應g(x，y)是濾波器系數與該濾波器所包圍的圖像像素乘積之和:

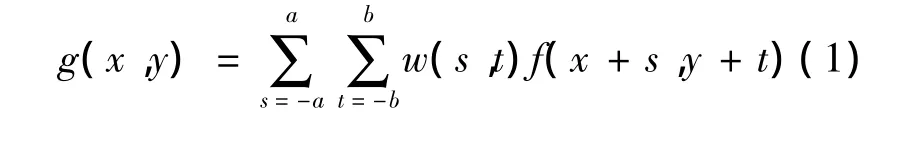
2 疵點圖像的判定

文中使用小波能量對地毯圖像中是否存在疵點進行判斷。小波是傅立葉分析的發展，二維的小波變換可以分離為對圖像數據的行和列分別作一維的小波變換;每次濾波后的下采樣使數據總量保持不變。所以小波變換的方法可以很方便地應用于疵點的實時檢測中，同時小波變換具有良好的時頻局部特征，對奇異信號有很好的檢測能力。地毯圖像中正常織物紋理信號可以看成是平穩光滑的低頻信號，而疵點區域因為灰度值的突變，而成為高頻信號。對疵點圖像進行小波分解，提取其高頻細節分量，對細節圖像進行小波能量的計算便可以判斷出圖像中是否有疵點的存在［4］。

2.1 二維離散小波變換檢測原理

二維小波將紋理圖像在不同尺度的伸縮和平移變換中每一層次的圖像都分解為4個不同頻率的圖像，其中包含1個平滑逼近子圖像和3個細節分量圖像，每個圖像為原圖像的四分之一大小［5］。設二維圖像信號為f(x，y)，則二維小波變換的快速分解算法為:

文中采用小波3級分解地毯圖像。如圖1所示，其中LL是平滑逼近，LH是垂直細節分量，HL是水平細節分量，HH是對角細節分量［6］。

圖1 二維小波三層分解示意Fig.1 Schematic diagram of three-layer decomposition of two-dimensional wavelet

經過小波分解后，各細節的能量可以分別表示為［7，9］:

第i層近似細節圖像的能量:

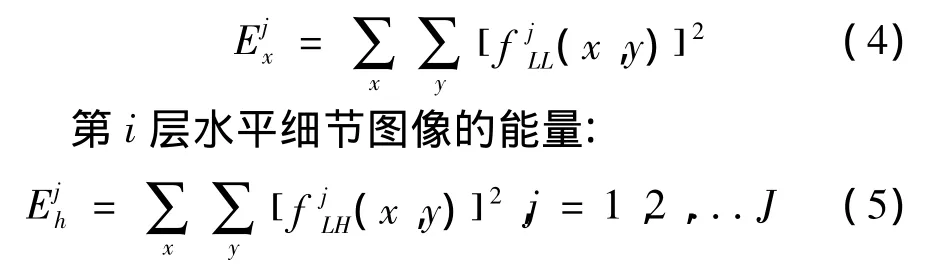
第i層垂直細節圖像的能量:

取一組無疵點地毯圖片，根據小波分解得到的細節圖像，分別計算各圖片的能量值，并設定一個能量值作為判斷有無疵點的依據。地毯疵點的判定準則為:設常量ξ＞0，Ei為第i層子圖能量，LevelN為分解總層數，當對某一i值成立時，可判定該圖像中包含有疵點。

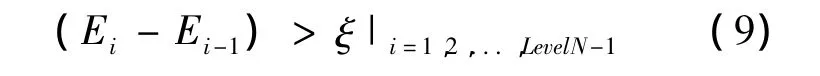
3 疵點分割

文中使用Otsu法實現疵點圖像的自動閾值分割，Otsu算法是在判決分析最小二乘法原理的基礎上推導出來的，是比較常用的計算方法［8］。

設圖像中灰度為i的像素數為ni，灰度范圍為［0，L-1］，則總的像素數為 N= ，各灰度值出現的概率為:Pi=ni/N。

把圖像中的像素用閾值T分成兩類C0和C1，C0由灰度值在［0，T-1］的像素組成，C1由灰度值在［T，L-1］的像素組成，則兩個區域的總方差為:

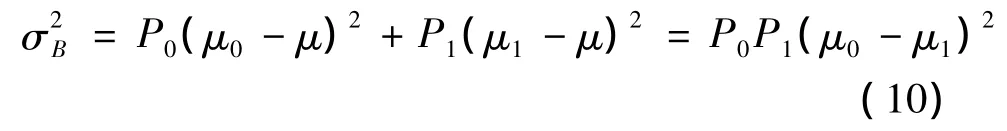
式中，讓T在［0，L-1］范圍內取值，使σB2最大的T值便是最佳區域分割閾值。

使用此方法不需要人為設定其他參數，是一種自動選擇閾值的方法。由于地毯表面粗糙，閾值的選擇與地毯的紋理粗細、密度等密切相關，僅僅使用自動閾值不能得到很好的效果，所以根據實際情況將閾值設定為自動閾值的0.56倍。

4 疵點檢測測試

對采集到的地毯圖像進行測試，其中圖2(a)～(c)為正常地毯圖像，圖2(d)～(i)為有跳紗疵點的地毯圖像。

圖2 地毯樣品Fig.2 Carpet samples

根據對無疵點地毯圖像的測試結果可設定ξ為1 000，則對地毯樣品圖的判定結果如表1所示。

將含有疵點的地毯圖像進行二值化并提取疵點，由于簇絨地毯的紗線較粗，約為2.5 mm，所以測試中將直徑小于3 mm的疵點視為正常紋理部分，對于小的疵點區域采用空洞填充使其成為背景紋理，得到二值化結果如圖3所示。

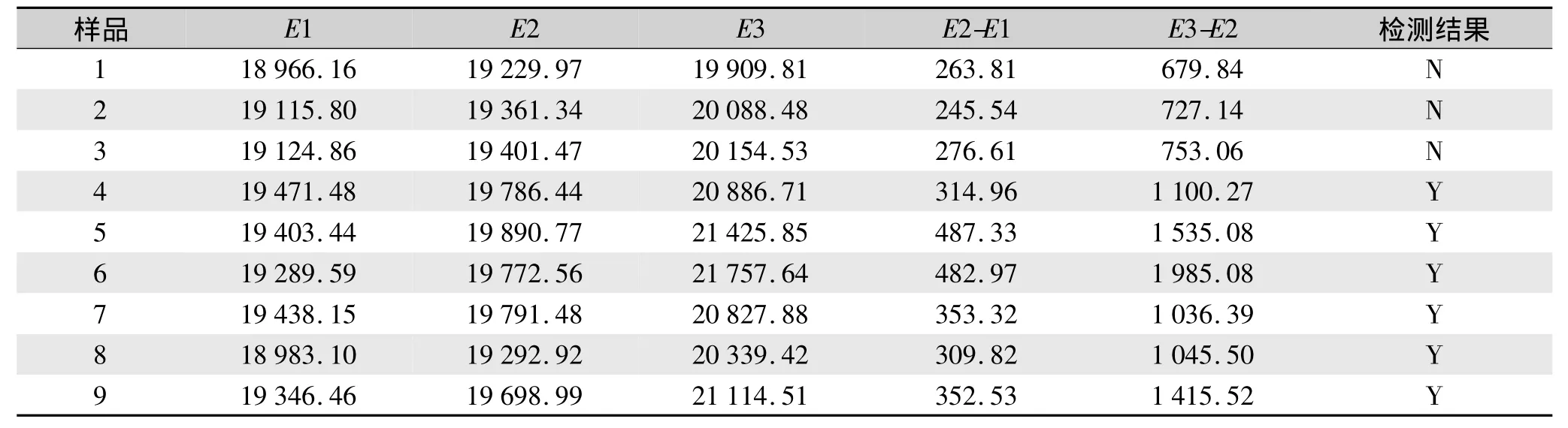
表1 地毯樣品測試結果Tab.1 Test results of carpet samples

為了方便檢測，根據二值化結果將疵點部分在源圖像的灰度圖中進行定位，首先采用sobel邊緣檢測算子提取疵點的輪廓，將得到的輪廓信息在灰度圖中進行疊加，定位結果如圖4所示。

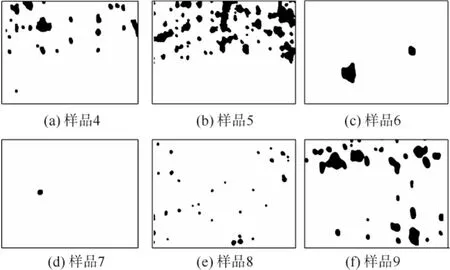
圖3 地毯樣品圖二值化結果Fig.3 Binaryzation result of carpet samples

圖4 地毯疵點定位結果Fig.4 Positioning result of carpet defects

5 結論

本文針對簇絨地毯的跳紗類疵點圖像，設計了一種基于小波能量的算法，將采集到的地毯圖像經小波3層分解得到各級細節子圖，計算各子圖的能量值。通過與正常圖像細節子圖的能量值比對判斷所檢測的圖像中是否含有疵點，對含疵點圖像進行二值化，并在源圖像的灰度圖中進行疵點定位，最后通過實驗驗證了此方法的可行性，此方法可以有效地將地毯圖像中的跳紗類疵點檢測出來。

［1］OM H，BISWAS M.An improved image denoising method based on wavelet thresholding［J］.Journal of Signal and Information Processing，2012，3(1):109-116.

［2］蔣蕾，尹業安，常利利.一種基于計算機視覺的織物疵點自動檢測方法［J］.計算機與現代化，2008(12):153-156，159.JIANG Lei， YIN Yean， CHANG Lili. Anautomatic processing method to inspect and recognize fabric defects based on computer vision inspection［J］.Computer and Modernization，2008(12):153-156，159.

［3］步紅剛，黃秀寶.基于計算機視覺的織物疵點檢測的近期進展［J］.東華大學學報:自然科學版，2006，32(3):128-133.BU Honggang，HUANG Xiubao.Recent research of fabric defect detection based on computer vision［J］.Journal of Donghua University:Natural Science Edition，2006，32(3):128-133.

［4］BELGE M，KILMER M E，MILLER E L.Wavelet domain image restoration with adaptive edge preserving regularization［J］.IEEE Transactions on Image Processing，2000，9(4):597-608.

［5］NGAN H Y T，PANG G K H，YUNG N H C.Automated fabric defect detection-A review［J］.Image and Vision Computing，2011，29(7):442-458.

［6］BANHANM M R，KATSAGGELOS A K.Spatially adaptive wavelet-based multiscale image restoration［J］. IEEE Transactions on Image Processing，1996，5(4):619-634.

［7］LI W C，TSAI D M.Wavelet-based defect detection in solar wafer images with inhomogeneous texture［J］.Pattern Recognition，2012，45(2):742-756.

［8］VIJAVAREKHA K. Segmentation techniques appliedto citrus fruit images for external defect identification［J］.Research Journal of Applied Sciences(Engineering and Technology)，2012，4(24):5313-5319.

［9］馬鑫宇，林意.基于小波子圖映射的疵點織物判定方法［J］.計算機工程與應用，2012，48(6):166-168，195.MA Xinyu，LIN Yi.Defect fabric determining based on wavelet subgraph mapping［J］.Computer Engineering and Applications，2012，48(6):166-168，195.