基于復合暗標拍賣的工程量清單招標模式

呂 煒，賀昌政，丁時勇

(1.四川大學工商管理學院，四川成都 610064;2.重慶市審計局，重慶 401177)

基于復合暗標拍賣的工程量清單招標模式

呂 煒1，2，賀昌政1，丁時勇2

(1.四川大學工商管理學院，四川成都 610064;2.重慶市審計局，重慶 401177)

針對投標人在工程量清單招標的不平衡報價問題，文章在研究暗標拍賣理論招標的基礎上，提出了將暗標一級、二級和三級密封拍賣結合起來建立復合暗標拍賣工程量清單招標合同清單招標模式。然后運用博弈論分析了投標人在工程量清單招標模式下的最優戰略就是不平衡報價，接著證明了復合暗標拍賣工程量清單招標能有效減少投標人的不平衡報價給招標人帶來的不利影響，節約工程投資。最后通過案例驗證了模型的證明。

暗標拍賣;工程量清單招標;模式

招標與投標活動起源于18世紀的英國，世界各國政府于19世紀初開始在工程建設領域實行招投標制。中國于20世紀80年代開始逐步在建設領域推行招投標制度，2000年頒布實施的《中華人民共和招標投標法》標志著中國建設工程招投標邁入了規范化發展階段。隨后為了與國際接軌，中國于2003年7月開始在工程建設領域實行工程量清單招標。國際上有不少國家和組織均采用此種招標方法，如英、美等發達國家。在工程量清單招標模式下，招標人提供工程量清單細目及相應的工程量，并對此負責，結算時按清單細目工程量按實結算，而投標人競標時填報的清單細目單價一般不予調整。但在工程招投標實踐中，投標人通常具有多年的工程建設經驗，其對工程變更的預測能力遠勝招標人，因此一些投標人利用工程量清單招標數量按實結算的特點采取不平衡報價，即在確定投標總報價的前提下，有意識地調整某些清單細目單價，旨在從工程變更(設計變更或地質條件變更)中獲得額外的收益，這就給招標機制設計帶來了新的挑戰。

當前，建設項目招標通常是采用一級密封拍賣的逆向形式，一些專家學者研究了基于價格(一維)信息的投標報價模型與策略［1-5］，也有學者以投標人的報價及相應的交易成本作為招標的商務目標函數，工程質量和工期等要求作為技術條件，并構建了與招標模型相適應的評標程序［6］;Che研究了基于價格和質量的二維招標模型［7］，隨后Branco等研究了多維信息拍賣招標機制［8-9］，趙冬梅等研究了多維信息招標模式下招標代理機構與投標人的串謀的博弈模型，研究結果表明通過加強懲罰力度等措施能降低腐敗發生的概率［10］。上述研究均未涉及投標人的不平衡報價問題。盡管也有一些學者研究了不平衡報價問題，但其主要研究基于一級密封拍賣招標的不平衡報價策略［11］，未從機制設計層面去考慮如何設計一個拍賣招標機制，以減輕或消除投標人的不平衡報價給招標人帶來的不利影響。在建設工程招標過程中，參加競標的投標人的工程成本是潛在投標者心中的秘密，這就導致招投標的不完全信息問題。為了解決不完全信息的投標人不按其真實成本報價問題，Vickrey于1961年提出了一種有效的帕累托拍賣機制，二級密封價格拍賣［1］，這種拍賣機制下，投標人的占優策略是按其真實支付出價(“說真話”)。但Robinson研究發現，二級密封價格拍賣更容易導致投標人合謀損害招標人利益［12］，而且一旦放棄招投標雙方的風險中性假設，一級密封價格拍賣與二級密封價格拍賣相比就具有某種優勢，因此風險厭惡的招標人更愿意選擇一級密封價格拍賣［13］。

建設工程招標是暗標拍賣的逆向形式，且根據投標人的總報價來確定贏標人，工程量清單招投標的一個特點就是通過招投標確定工程量清單細目價格，招標工程數量僅供投標報價參考，這就為投標人的不平衡報價提供了機會［11］。而不平衡報價的實質就是低價中標，高價結算，增大工程投資，因此有必要設計一個招標機制，以減輕或消除不平衡報價給招標人帶來的不利影響。筆者在上述文獻研究的基礎上，將暗標拍賣理論予以擴展，構建了基于復合暗標拍賣的工程量清單招標模式。與Che［7］研究的包含質量與價格二維信息拍賣招標不同，本招標模式屬于一維(價格)信息招標，但與傳統一維信息拍賣招標略有不同，傳統拍賣招標贏標人的清單細目價格系其自身清單細目價格，而本招標模式下中標人的清單細目價格系由贏標人自身填報清單細目價格與第二及第三低投標人清單細目價格的復合而成。

論文首先在介紹暗標拍賣的基礎上提出了復合暗標拍賣工程量清單招標，接著運用博弈理論分析了投標人在工程量清單招標模式下的最優投標戰略就是采取不平衡報價戰略，隨后論文證明了復合暗標拍賣工程量清單招標能有效減少不平衡報價給招標人帶來的不利影響，接著通過案例驗證了論文提出的招標模式，最后是論文的結論。

一、基于復合暗標拍賣的工程量清單招標模式

拍賣或招標的基本功能有兩個:一是揭示信息，二是減少代理成本。現有的拍賣方式很多，基本的拍賣方式分為公開口頭拍賣和暗標拍賣，而暗標拍賣(sealed bid auction)是指參與拍賣的競標人在互不知道其他競標人報價的情況下各自密封出價，統一時間開標，價高者中標。暗標拍賣方式又可分為一級密封價格拍賣(the first-price sealed auction)、二級密封價格密封拍賣(the second-price sealed auction)和 k 級密封價格拍賣［1］。

一級密封價格拍賣是指投標人(bidders)同時將自己的出價寫下來裝入一個信封，密封后交給拍賣人，拍賣人打開信封，出價最高者是贏者，按他的出價支付價格，拿走被拍賣的物品。二級密封價格拍賣也稱為Vickrey拍賣，其程序與一級密封價格拍賣基本一致，唯一不同的就是報價最高者中標，但其支付價格為第二高價。第k(k=1，2，…，K )價格暗標拍賣與二級密封價格拍賣一樣，其拍賣程序與一級密封價格拍賣基本相同，招標人打開信封后，報價最高者贏得拍賣物，其支付價格為比投標人報價低的第k價格。如在拍賣品市場上參與競拍的投標人有n家，其報價由高到低的排序為b1≥b2≥…≥bk≥bk+1…≥bn，所謂第k價格是指報價為b1的投標人贏得拍賣物，但其結算價格為bk。

從上述暗標拍賣方式來，決定中標人的關鍵就是拍賣(或招標)的總報價。筆者針對暗標拍賣這一特點，提出了基于復合暗標拍賣的工程量清單招標模式:競價程序是投標人將自己的技術方案(含商務文件)和報價寫下來，分別裝入不同的信封，密封后按招標文件約定遞交給招標人或招標代理機構，評標委員會先評技術方案，然后打開技術方案評審合格的投標人報價信封，報價最低者贏得建設工程承包合同，其投標報價即為合同支付價格，其他投標人支付為零，但中標人清單細目價格按以下方式確定:(1)當中標人i(即其投標報價最低時，但低于成本除外)、次低投標人與第三低投標人同一清單細目單價不呈同規律變化(即報價最低的三個投標人相同清單細目單價不存在)時，則中標人合同清單細目修正價格為投標人i、次低投標人與第三低投標人的清單細目單價加權之后乘以一個調整系數δ1;(2)當中標人i、次低投標人與第三低投標人同一清單細目單價呈同規律變化時，則中標人合同清單細目修正價格為投標人i、標底清單細目單價加權之后乘以一個調整系數δ2。即修正清單細目子項單價p1ji為:

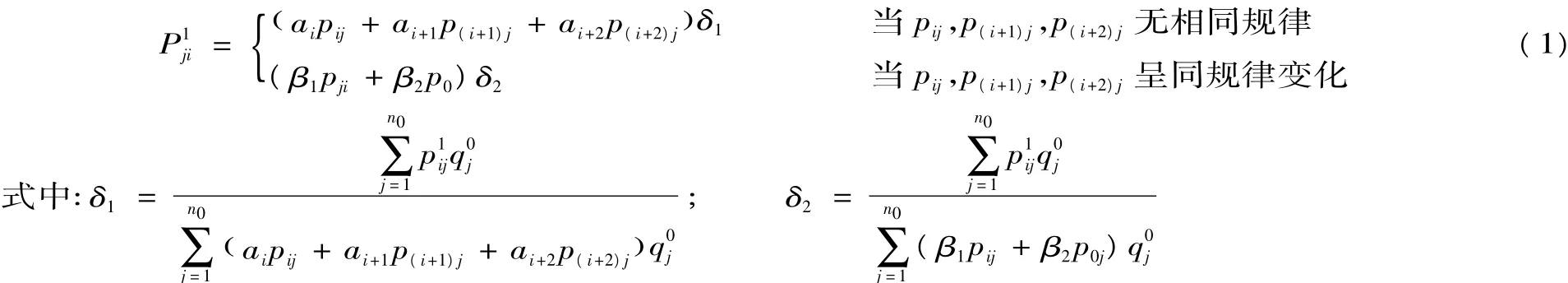
pij為投標人i的第j項清單細目單價;p0j為標底第j項清單細目單價;為第j項清單工程數量;n0為招標清單細目數量;0≤αi，αi+1，αi+2≤1 且 αi+αi+1+ αi+2=1;0 ≤ β1，β2≤1 且 β1+ β2=1。

αi，αi+1，αi=2，β1，β2的值可采取指數平滑法或根據招標人經驗確定，稱為先驗值，然后再通過招投標實踐進行修正。顯然，當αi=1或β1=1即為一級密封拍賣招標，而αi，αi+1，αi=2，β1，β2∈0，()1為新的招標模式。因此論文所討論的基于復合暗標拍賣的工程量清單招標模式，實際上是一種新的招標模式。

二、基于復合暗標拍賣的工程量清單招標模型

模型基本假設:(1)假設所有投標人都是風險中性的;(2)假設招標人先評技術標，技術標合格的投標人才能進行投標報價，確定最后的贏標人，論文根據國際慣例，采取低價中標;(3)假設所有投標人不存在合謀和共同知識。

因此模型的建立與經典一級密封拍賣招標模型相同，只是投標人的效益函數包括了工程變更收入。工程變更收入通常包括兩部分:一是工程量清單細目數量變更;二是工程變更導致新增工程量清單細目(即工程變更導致原有工程量清單細目單價不適用而需要重新組價的工程量清單細目)。而后者的清單細目單價通常可認為是甲、乙雙方根據招標文件或合同條款約定重新租價。為了簡化分析，論文僅考慮清單數量變更增加收入，那么投標人的期望支付為:

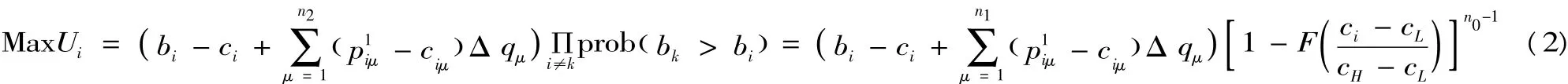
式中:bi為投標人i的投標總報價;ci為投標人i完成招標工程量清單全部內容的成本;n2為工程結算時發生數量變更的清單項數;p1iμ為投標人 i第 μ項清單細目修正單價;ciμ為投標人i完成第μ項清單的單位成本;Δqμ為第μ項清單細目工程量增減數量;cL為所有投標人完成招標工程量清單全部內容的最小成本;cH為所有投標人完成招標工程量清單全部內容的最大成本;n1為參與競標的人數。

三、投標人的投標報價策略分析

對投標人來說，先根據招標工程量清單細目測算工程成本，并結合其他人的報價決定整體報價;然后根據總報價、清單細目成本、現場踏勘以及投標人經驗確定各清單細目報價。投標人所提供的報價不僅包括總投標報價，而且包括清單細目單價。由于均衡時贏標人所提供的總報價與其自身成本和其他投標人的私有信息相關，而其提供的清單細目單價僅與其自身的清單單位成本、工程實際情況以及經驗確定，因此在投標過程中，贏標人在確定總體報價水平時需要考慮其他競標人的整體報價水平。

命題1:一級密封價格拍賣工程量清單招標基準模型，投標人存在對稱的Bayes-Nash均衡，總投標報價策略，就是b*()c，即(5)式;在總報價金額一定時，不平衡報價是投標人的弱占優戰略。在此戰略下，通過提高其預測設計變更導致清單細目工程量增加的清單細目子項報價，減少預測設計變更導致清單細目工程量減少的清單細目子項目報價，即可增加其結算期望收益。

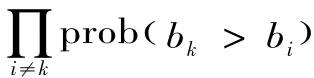
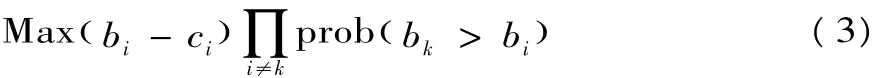
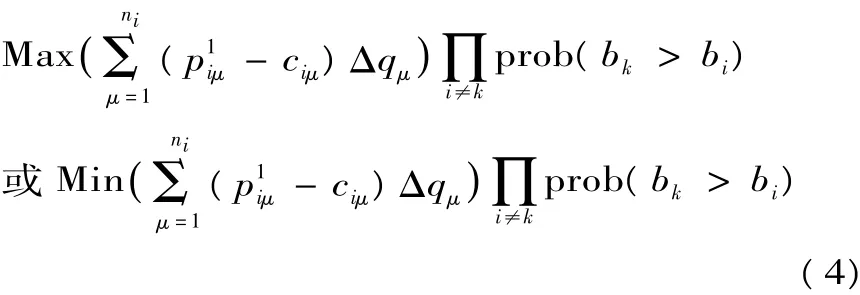
因此其均衡報價策略，可以通過(3)式對ci求導，并令其等于零即可得到微分方程，解此微分方程即可得到均衡投標報價，因此投標人的最優總報價策略為［6］:

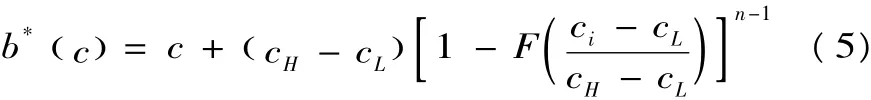
接著證明在均衡整體報價水平下，投標人通過采取不平衡報價戰略即可增加其工程結算期望收益。由前文知，在一級密封價格拍賣工程量清單招標模式下，αi=1，于是=piμ，因此有 piμ-ciμ≥0，即投標人清單細目單價大于完成該清單細目單位成本。

當Δqμ=0時，結算時所有清單細目工程數量保持不變。無論piμ值如何變化，( piμ-ciμ)Δqμ=0，投標人無論采取不平衡報價與否，其結算收益均相等。

當Δqμ＞0時，結算時該項清單細目工程數量增加:因此增加工程結算收益就是最大化(4)式，即增大 ( piμ-ciμ)函數值。因此當ciμ取值一定時(即投標人完成某一清單細目的單位工程成本為一常數)，函數 ( piμ-ciμ)Δqμ是 piμ的 增 函 數，piμ值 越 大，( piμ-ciμ)Δqμ函數值也就越大。所以投標人提高結算工程量清單細目工程數量增加子項的清單細目單價，即可增大其結算收益。

當Δqμ＜0時，結算時該項清單細目工程數量減少，因此增加工程結算收益就是最小化(4)式，即減少 ( piμ-ciμ)Δqμ函數值。因此，當 ciμ取值一定時，函數 ( piμ-ciμ)Δqμ是 piμ的 減 函 數，piμ值 越 小，( piμ-ciμ)Δqμ函數值反而越大。所以投標人減少結算工程量清單細目工程數量，減少子項的清單細目單價，即可增大其結算收益。

綜上所述，當b*(c)值一定時，不平衡報價是投標人的弱占優戰略。

證畢。

命題1的結論與David W C，Paul A B和Ammar P K的研究結論相似［11］，他們通過案例解析得知不平衡報價將給投標人帶來額外收益;而筆者通過運用博弈理論分析不完全信息條件下均衡時投標人的報價策略發現，不平衡報價是投標人的弱占優戰略。兩者研究方法雖然不同，卻得到類似的結論，即在工程量清單計價招標模式中，不平衡報價可以給投標人帶來額外收益。盡管David W C，Paul A B和Ammar P K分析了不平衡報價的三種類型，但卻未考慮設計一種拍賣招標方式，以減少或消除不平衡報價給招標人帶來的不利影響。筆者接下來分析復合暗標拍賣工程量清單招標模式給招標人帶來的影響。

命題2:在復合暗標拍賣工程量清單招標模式下，投標人同樣存在對稱的Bayes-Nash均衡總投標報價策略，就是b*()c;在總報價金額一定時，不平衡報價是投標人的弱占優戰略，在此條件下，投標人通過不平衡報價戰略可以提高其結算期望收益。但在同等條件下，投標人采取不平衡報價戰略增加的結算期望收益低于一級密封拍賣工程量清單招標采取此戰略的結算期望收益。

證明:首先，復合暗標拍賣的工程量清單招標模型與一級密封價格拍賣工程量清單招標基準模型不同點就是 αi，β1取值不同。前者中 αi，αi+1，αi=2，β1，β2∈0，()1，而后者αi=1或β1=1。兩者的均衡條件均是(3)式對ci求導，因此他們具有相同的整體報價戰略——對稱的Bayes-Nash均衡b*()c ，該均衡的具體求解見前一命題證明。

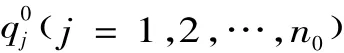
不妨假設結算時各清單細目工程數量如贏標人i所預計那樣，則:

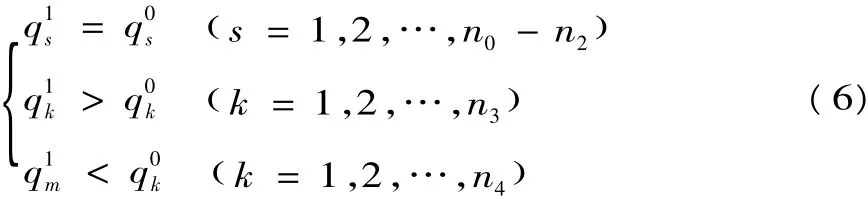
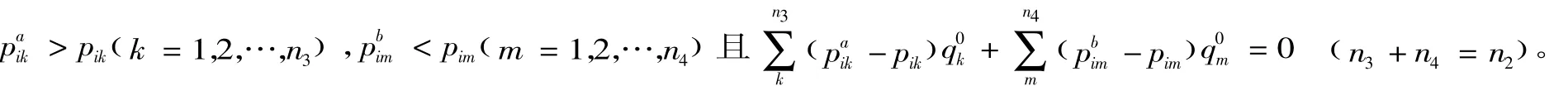
假設投標人不存在合謀，論文以報價最低三人各清單細目單價不呈同規律變化進行分析，如其相反，則可采取類似方法得到相同的結論。

又因αi，αi+1，αi=2∈0，()1，贏標人i采取不平衡報價戰略，其合同清單細目單價(即結算清單細目單價)為:

贏標人不采取平衡報價戰略，其合同清單細目 單價(結算清單細目單價)為:

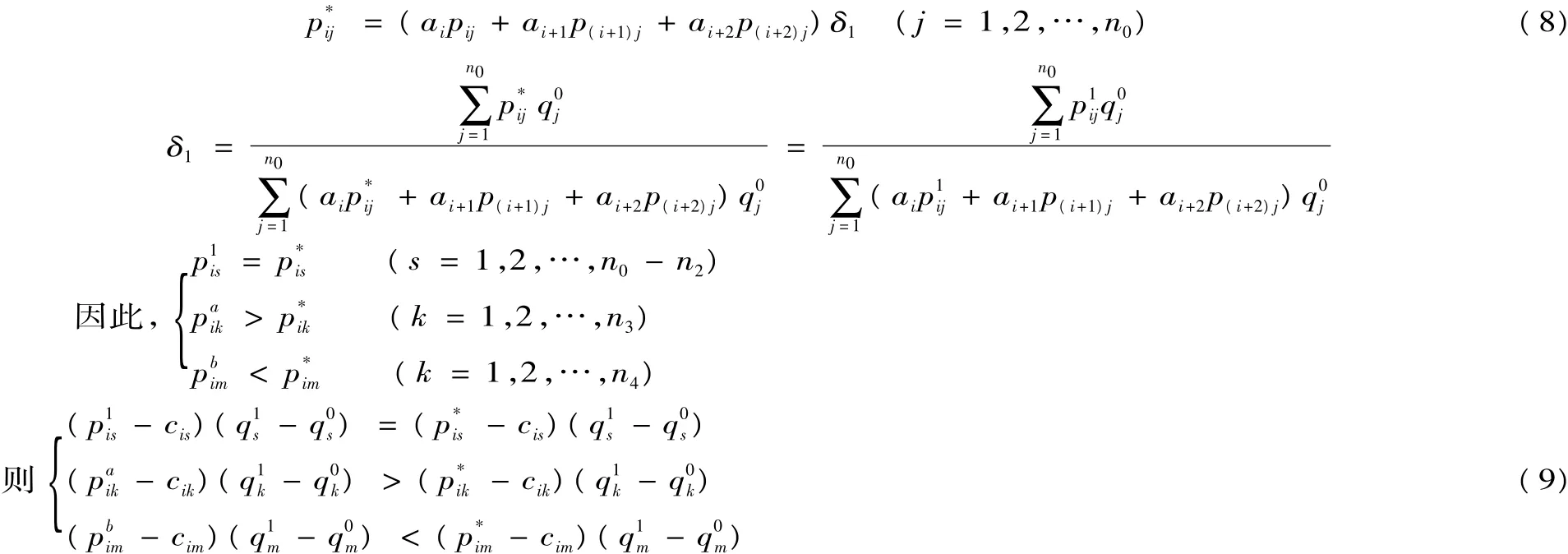
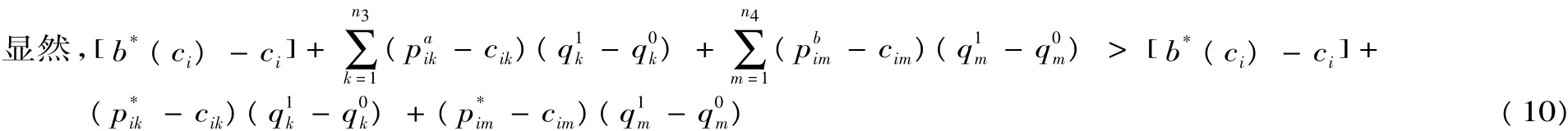
即不平衡報價戰略是贏標人i的占優戰略。

然后，分析比較復合暗標拍賣工程量清單招標和一級密封拍賣工程量清單招標投標人采取不平衡戰略的期望收益。

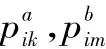
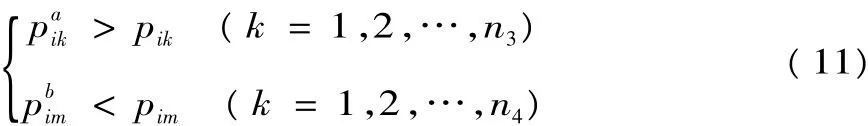
其中pik，pim分別為贏標人i采取不平衡報價戰略提高和降低的清單細目單價。因此:

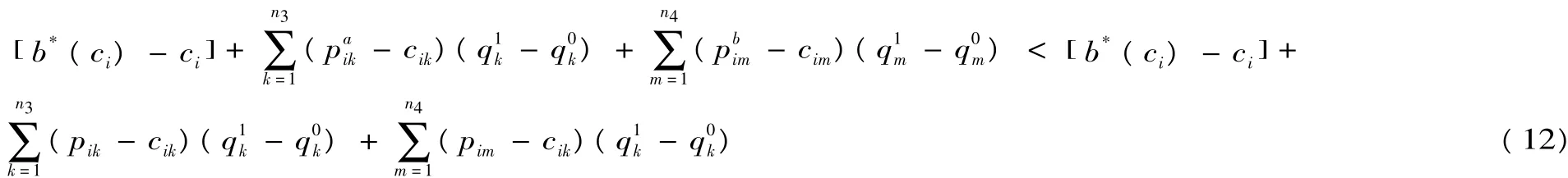
即在相同情況下，贏標人采取不平衡報價戰略增加的結算期望收益低于一級密封拍賣工程量清單招標采取此戰略的結算期望收益。

證畢。

Myerson研究了投標者的類型為一維的最優拍賣機制設計［18］，但該拍賣機制未考慮工程量清單拍賣招標的不平衡報價問題。而從命題2可以看出，招標人采用復合暗標拍賣工程量清單招標能減少或消除投標人不平衡報價給其帶來的不利影響，即可以減少支付。在復合暗標拍賣工程量清單招標模式下，贏標人的合同清單細目價格不僅與其自身私有信息有關，而且還與其他競標人的私有信息有關，因此有必要分析命題2中所體現的經濟含義。

首先在不考慮工程數量變更的條件下，交易達成之后承包商的生產剩余為

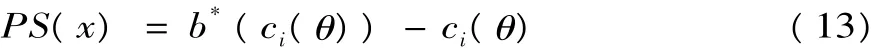
而在考慮工程數量變更的條件下，此時工程數量變更勢必影響承包商的支付，此時承包商的生產剩余為

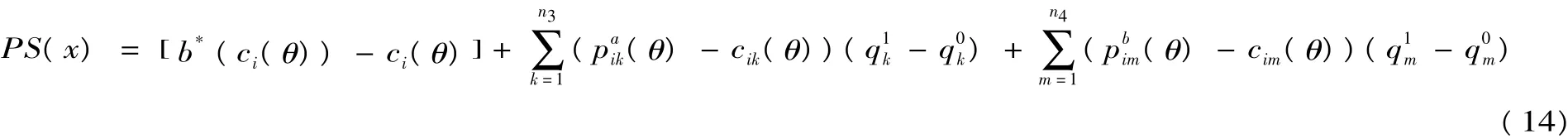
從上式可知:第一項為不存在工程變更時贏標人的生產剩余;第二項為清單細目工程量增加的生產剩余;第三項為清單細目工程量減少的生產剩余。在類型θ確定后，(θ)-cik(θ)為工程量增加清單細目k的邊際收益，而(θ)-cim(θ) 為工程量減少清單細目m的邊際收益。為簡化分析，論文僅分析pij，p(i+1)j，p(i+2)j不呈同規律變化的情形，將(aipij+ai+1p(i+1)j+ai+2p(i+2)j)δ1代入，則工程量增加清單細目k的邊際收益為

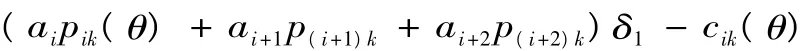
由命題2的證明知，要增大贏標人工程量增加清單細目 k的邊際收益就是得增大 aipik(θ) +ai+1p(i+1)k+ai+2p(i+2)k，而 ai，ai+1，ai+2，p(i+1)k，p(i+2)k均是贏標人的外生變量，因此贏標人唯一最優策略就是盡可能提高其報價。在工程實施過程中，贏標人的支付等于招標人的支付，增大贏標人的支付就相應減少了招標人的支付。因此站在招標人的角度就是減少 aipik(θ) +ai+1p(i+1)k+ai+2p(i+2)k，而 pik(θ) 是贏標人的報價，p(i+1)k，p(i+2)k則為報價第二、三低投標人的清單細目單價，上述三者均是招標人的外生變量，招標人的最優決策就是選擇合適的ai，ai+1，ai+2，以減少自己的支付。對理性的招標人來說，他知道贏標人的最優報價是盡可能提高清單細目工程量、增加清單細目單價pik(θ)，因其最優戰略就是減少ai的權重。當ai=1時，贏標人的合同清單細目單價完全由贏標人填報的清單細目單價決定，即傳統一級密封拍賣工程量清單招標為復合暗標拍賣招標的特殊形式;當ai=0時，贏標人的清單細目單價由第二、三低投標人清單細目單價決定，此時工程量增加清單細目k的邊際收益 (ai+1p(i+1)k+ai+2p(i+2)k)δ1-cik(θ)，即為信息租金，其產生的根源是信息不對稱。潛在投標人擁有自己的私人成本信息，因而這種信息租金是招標人所必須向贏標人支付。招標人減少信息租金的有效辦法就是增加競爭，因此復合暗標拍賣工程量清單招標的關鍵就是確定 αi，αi+1，αi=2，β1，β2值，其方法很多，有簡單平均法、移動加權平均法以及指數平滑法等，招標人還可以根據自己的經驗或已有的信息進行確定，然后在招投標實踐中予以修正。同理，可對工程量減少清單細目m的邊際收益進行類似分析。

在復合暗標拍賣工程量清單招標模式下，合同總是授予成本最低的競標人，因此這個最終分配是有效的。命題2還表明，招標人采取復合暗標拍賣工程量清單招標，只要 αi，αi+1，αi=2，β1，β2值選擇合理，就能減少支付，增大其期望收益。

四、案例驗證

為了直觀理解論文提出的復合暗標拍賣工程量清單招標，現給出一個具體的算例來說明其運行方式。假設某政府工程進行招標，業主單位的招標工程量清單見表1第1欄內，共有11個投標人參與競標，其中技術標審查合格的投標人有8家，將贏標人的正常報價計入表1第3欄內，將贏標人的不平衡報價以及另外兩個報價最低的工程量清單細目單價分別填入表1第4欄、第7欄和第8欄內。

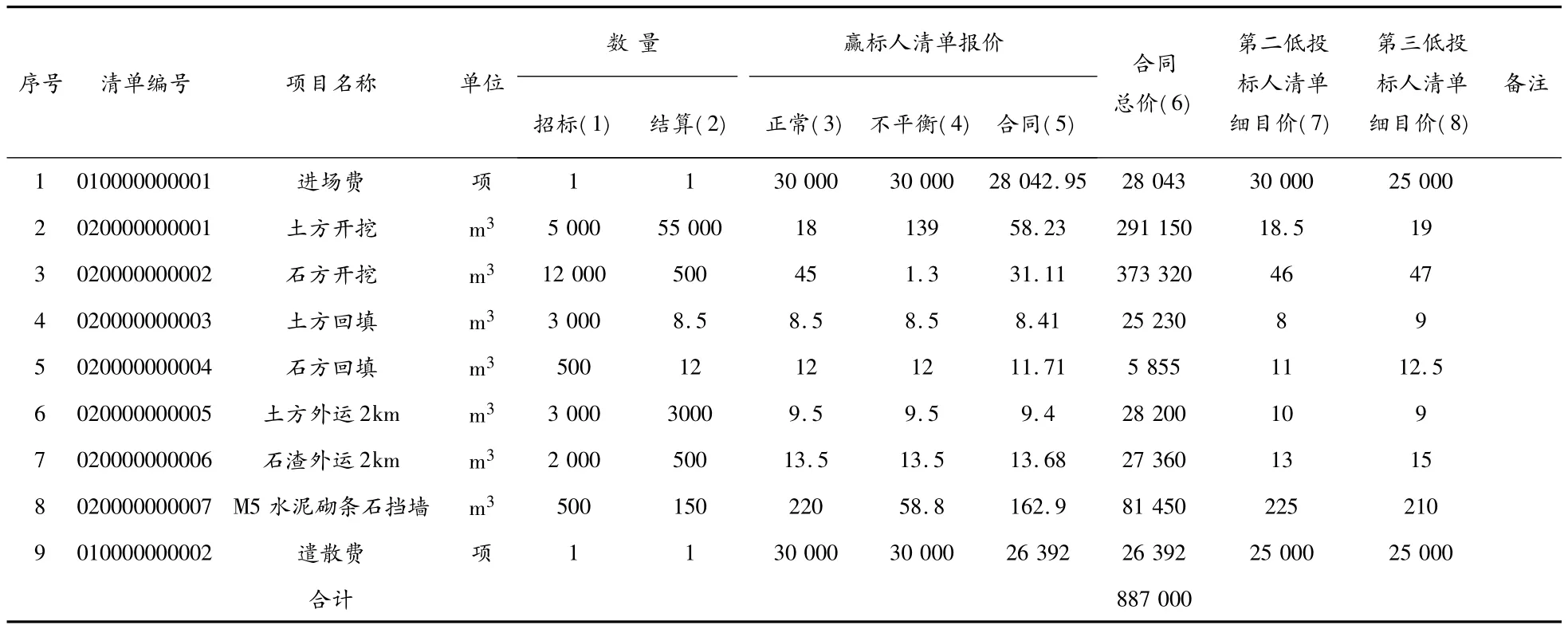
表1 復合暗標拍賣工程量清單招標報價表 金額單位:元

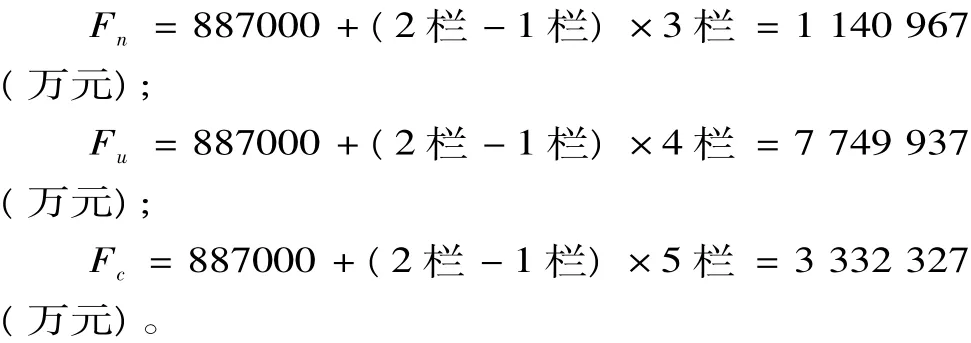
顯然，Fu＞Fc＞Fn，即站在投標人的角度，當投標總報價確定之后，采取不平衡報價是占優策略，而筆者提出的招標模式可以減少投標人的不平衡報價給招標人帶來的影響，間接驗證了論文的證明。

五、結論

論文基于暗標拍賣理論，將暗標一級、二級和三級密封拍賣結合起來，建立了復合暗標拍賣工程量清單招標合同清單招標模式。接著運用博弈理論的基本原理分析了競標人在一級密封拍賣工程量清單招標和復合暗標拍賣工程量清單招標的報價策略，競標人投標總報價確定以后的最優報價策略就是采取不平衡報價。隨后論文證明了站在招標人的角度，復合暗標拍賣工程量清單招標能有效消除投標人不平衡報價戰略的影響，節約工程投資。最后通過案例驗證了論文的證明。

論文針對投標人在工程量清單的不平衡報價問題，提出復合暗標拍賣工程量清單招標模式。既豐富充實招投標理論，又能減少不平衡報價給招標人帶來的影響，節約工程投資。但在工程招投標實踐中，由于競標人已承攬的工程任務以及建筑區域等因素的影響，很難確定一種最優的招標模式，應根據工程實際予以選擇。

［1］VICKERY W.Counterspeculation，auction and competitive sealed tenders［J］.Journal of Finance，1961，16(1):8-37.

［2］FRIEDMAN L.Competitive-bidding strategy［J］.Operation Research，1956，82:104-112.

［3］GATES M.Bidding strategies and probabilities［J］.Journal of Construction Division，1967，93:75-107.

［4］ IRTISHAD A.Decision-support system for modeling bid/no-bid decision problem［J］.Journal of Const ruction Engineering and Management，1990，116:595-608.

［5］呂煒，任玉瓏，季玉華.基于一級密封的工程量清單投標報價的博弈模型［J］.管理工程學報，2007(1):122-126.

［6］王卓甫，楊高升，刑會歌.建設工程招標模型與評標機制設計［J］.土木工程學報，2010(8):140-145.

［7］CHE Y K.Design competition through multi-dimensional auctions［J］.RAND Journal of Economics，1993，24:668-680.

［8］BRANCO F.The design of multidimensional auctions［J］.RAND Journal of Economics，1997，28(1):63-81.

［9］王宏，陳宏明，楊劍俠.多維信息招投標中的最優機制及其實施［J］.管理科學學報，2010(8):1-14.

［10］趙冬梅，王園園.多維信息招標下招標代理機構與投標方串謀的博弈模型及分析［J］.數學的實踐與認識，2012(8):28-37.

［11］CATTELL D W，BOWEN P A，KAKA A P.Review of unbalanced bidding models in construction［J］.Journal of Construction Engineering and Management，2007(8):562-573.

［12］ROBINSON M S.Collusion and choice of auctions［J］.Rand Journal Economics，1985，16:141-145.

［13］殷紅.多物品拍賣機制設計理論與方法［M］.上海:學林出版社，2009.

［14］MONDERER D，TENNENHOLTZ M.K-Price auction［J］.Games and Economics Behavior，2000，31(2):220-244.

［15］KLEMPERER P.Auction theory:a guide to the Literature［J］.Journal of Economics Surveys，1999，13(3):227-286.

［16］MONDERER D，TENNENHOLTZ M.K-price auctions:Revenue inequalities，utility equivalence，and competition in auction design［J］.Economic Theory，2004，24(2):255-270.

［17］MILGROM P.Putting auction theory to work［M］.Cambridge:Cambridge University Press，2004.

［18］MYERSON R B.Optimal auction design［J］.Mathematics of Operation Research，1981，6(1):58-73.

The Bidding Mode of Bill of Quantities Based on Composite Sealed-bid Auction

LYV Wei1，2，HE Changzheng1，SHI Yongding2
(1.School of Business，Sichuan University，Chengdu 610064，P.R.China;2.Chongqing Audit Bureau，Chongqing 401177，P.R.China)

At first， to aim at the unbalance bidding skill of tenders under the bill of quantities bidding mode，this paper puts forward the bidding mode of bill of quantities based on composite sealed-bid auction by study on basis of sealed-bid auction bidding theory.Secondly，the authors make use of game theory to analyze the bidders'optimal offer strategy which is unbalance bidding under the bidding model of bill of quantities.Thirdly，it is proven that the bidding mode of bill of quantities can effectively reduce the adverse effect which is bring by the tenders'unbalanced bidding， and to reduce the investment.At last， the authors validate the results of model by using the example.

sealed-bid auction;bill of quantities;bidding mode.

F22，F062.4

A

1008-5831(2013)02-0035-07

2012-09-17

呂煒，男，四川大學商學院博士研究生，主要從事項目管理、博弈論與信息經濟學研究。

(責任編輯 傅旭東)