基礎－結構耦合系統受地震作用的非線性振動

楊志安，常文潔，李高峰

（唐山學院 唐山市結構與振動工程重點實驗室，河北 唐山063000）

地震是一種自然災害，它對建筑物的破壞與基礎－結構耦合系統非線性響應有關。其中共振區的動力性質對建筑系統破壞作用的影響明顯。地震通常被看做下臥基巖上的周期激震源，通過上臥土層的傳遞途徑再被分解為一系列的激振頻率。［1］所以，作用于基礎和上部結構的地震荷載與地基土的性質有關，地基參數如土層厚度、剪切波速等的變化，會使結構上地震荷載的性質和量值有明顯的差異，從而產生結構地震響應動力性質的差異。特別對于非線性動力系統，地基參數引起的地震荷載變化，使系統的地震響應產生顯著差別。只有把地基和結構作為整體系統來考慮，記入土體－結構的動力相互作用，才能夠真實反映地基性質對結構地震特性的影響。［2－3］以下以文獻［4－6］為基礎，從系統能量出發，將基礎－結構作為整體考慮，應用分析力學原理推導系統的非線性動力方程，而后應用多尺度法分析系統的三頻率組合共振問題，并進行數值計算，比較系統不同參數變化對共振曲線的影響。

1 基本方程

圖1所示為基礎－結構耦合系統受地震激勵的簡化動力模型。其中地基為均勻的彈性土層，地震作用為下臥基巖的水平運動。與土體相比，結構的整體剛性較大，可以把結構視為地基上的質點－彈性桿（即彈簧）體系。圖1中，H代表地基土厚度，m代表質點的質量，k代表結構的等效彈簧系數，s（t）代表質點相對于地面的位移，ug（t）代表基巖的水平振動位移，η代表粘滯阻尼系數。

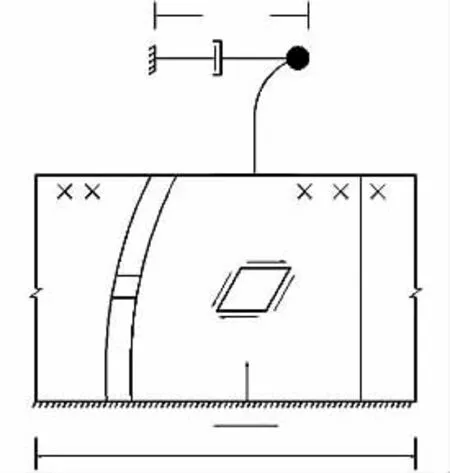
圖1 基礎－結構耦合系統地震分析動力模型

將結構和土體上的水平地震力可分別表示為

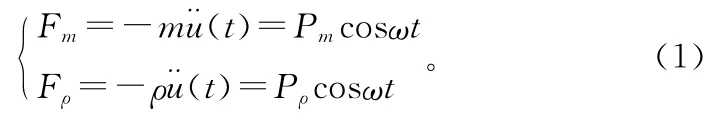
式中Pm＝αmg，g代表重力加速度，α代表水平地震影響系數；Pρ＝αρg，ρ代表土的質量密度，ω代表地震激振頻率。結構彈簧的性質與結構材料的性質有關，為了反映結構材料的非線性，把彈簧視為具有恢復力－變形關系的非線性彈簧，即

式中β代表彈簧的非線性因子。對于硬彈簧和軟彈簧的情況，β分別取正負值。

地基土對地震的反應為水平剪切運動，相對于基巖的剪切位移為u＝u（z，t）。以下把基礎和結構作為系統整體考慮，從能量角度出發，截取一定范圍進行計算，由分析力學拉格朗日方程導出系統在地震作用下的非線性動力學方程。當截取的計算范圍很大時，得到系統的動力學方程

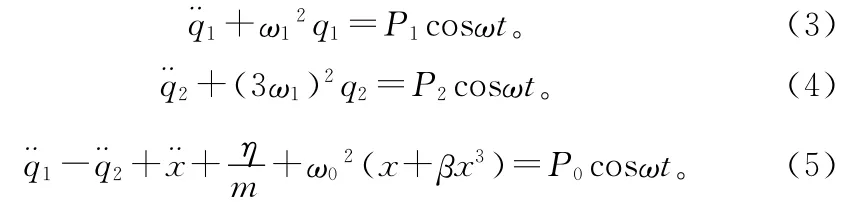
其中

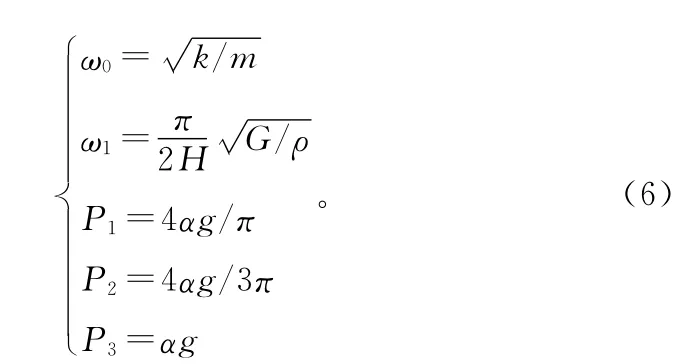
由式（3）解得

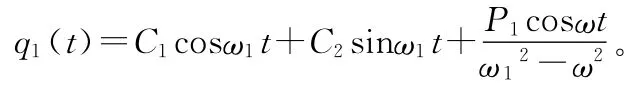
令t＝0時，q1（t）＝0，1（t）＝0，將其分別代入上式，得

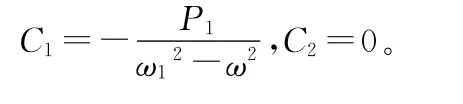
所以

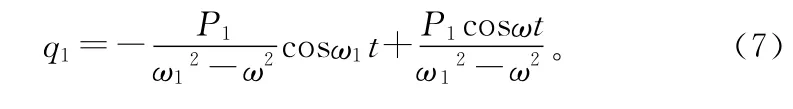
同理

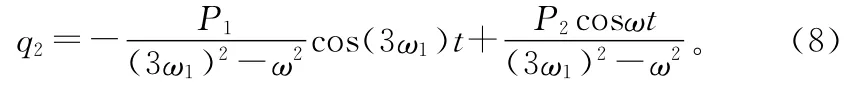
將式（7）和式（8）代入式（5），得

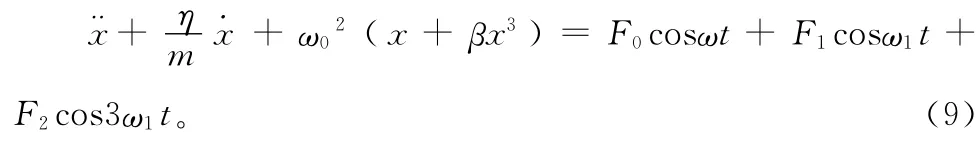
其中

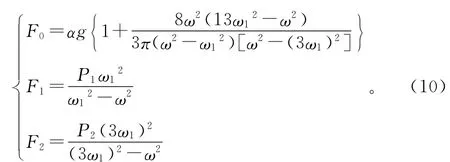
2 基礎－結構耦合系統的三頻率組合共振理論分析

以下以ω0≈ω＋ω1－ω2為例，分析組合共振，引入組合共振調諧參數σ，上述共振關系可表示為

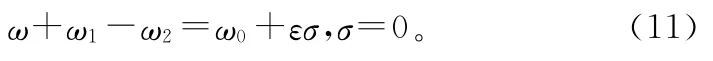
由多尺度法［7－9］得消除永年項的條件為

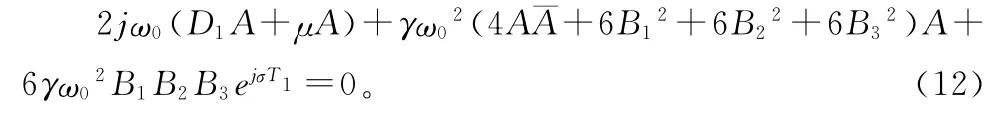
引入

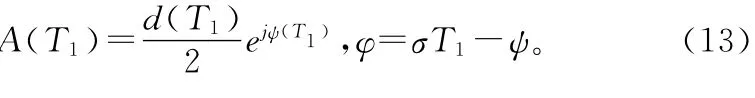
將式（13）中第一式代入（12）得

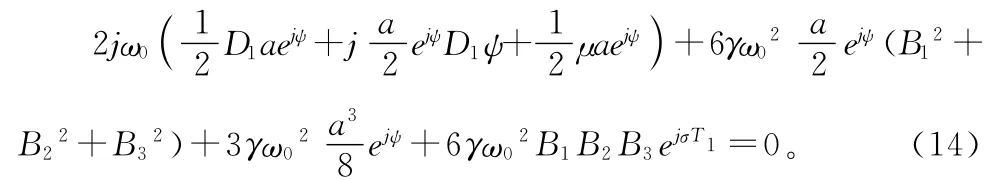
將式（13）中第二式代入上式并整理得

分離實部虛部后得到組合共振的慢時變振幅a和相位φ應滿足的自治微分方程組

其中

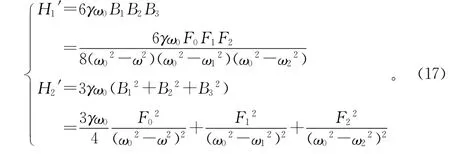
為確定對應穩態運動的定常解幅頻響應方程，在式（16）中令D1a＝0，D1φ＝0，得到振幅a和相位φ滿足的代數方程為

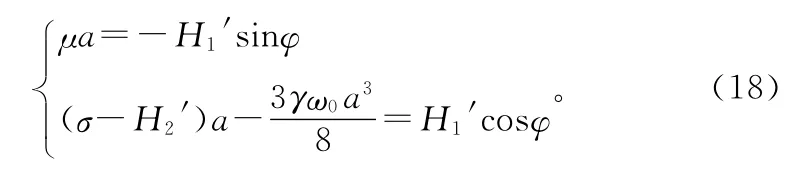
兩式平方后相加消去φ，得到組合共振的幅頻響應方程和相頻響應方程：

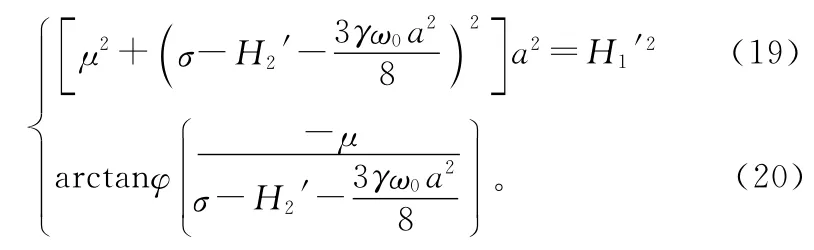
式（19）可以表示為

由式（19）可得組合共振的最大振幅：

它發生在

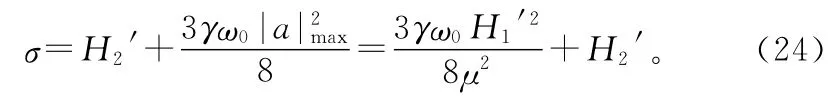
將方程（16）在（a，φ）處線性化，形成關于擾動量Δa和Δφ的自治微分方程：

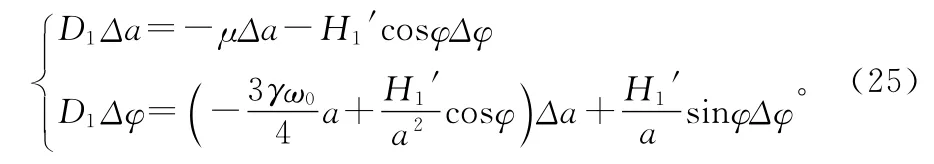
利用式（18）消去上式中的φ，得到

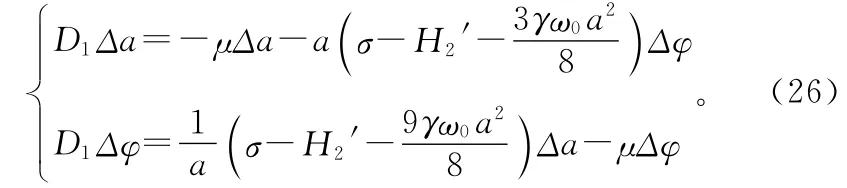
進一步得到特征方程：

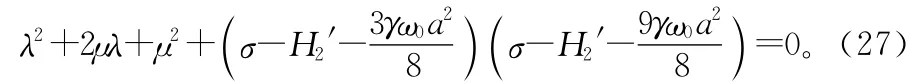
對于μ＞0，由Routh－Hurwitz判據可得定常解失穩的條件：

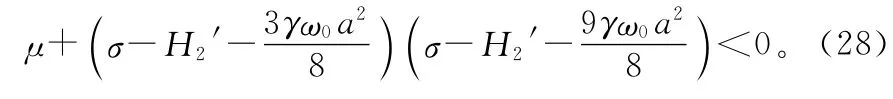
3 數值計算與結果分析

由式（10）和式（11）得

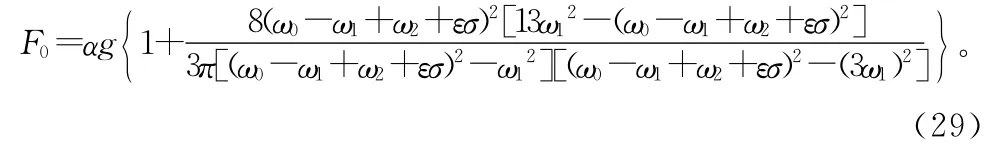
按式（21）可以繪制計算系統組合共振的各種響應曲線。圖2至圖7為不同參數條件下系統組合共振的幅頻響應曲線。

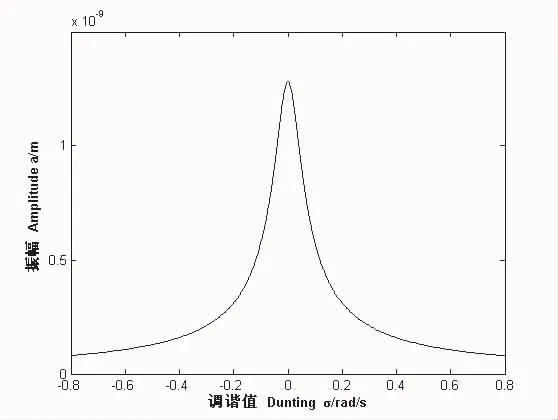
圖2 幅頻響應曲線

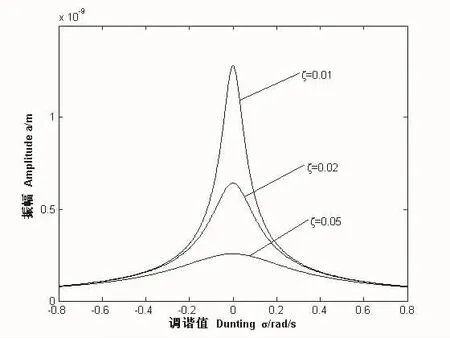
圖3 幅頻響應曲線（ξ）

圖4 幅頻響應曲線（H）

由圖2可知此種組合共振幅頻響應曲線不存在跳躍和滯后現象。圖3反映阻尼比對系統組合共振幅頻響應曲線的影響，由圖3可知減小阻尼比可以增大系統組合共振的振幅和共振區。圖4反映地基土層厚度對系統組合共振幅頻響應曲線的影響，由圖4可知減小地基土層厚度可以減小系統組合共振的振幅和共振區，H的變化會引起共振區的強烈變化。圖5反映剪切波速時系統組合共振幅頻響應曲線的影響，由圖5可知剪切波速越大，系統組合共振的振幅和共振區越小。圖6當改變彈簧非線性因子β的符號時，考慮振幅a與調諧值σ間的關系。從圖6中可以看出，只要β的數值確定，無論其是正還是負，系統的組合共振幅頻響應曲線均重合。結合式（29）可知，激勵幅值隨小參數ε的變化而變化，但是弱非線性的條件要求小參數ε的取值不應過大。當改變小參數ε時，考慮振幅α與調諧值σ間的關系。圖7為3種不同小參數取值時對應的系統組合共振幅頻響應曲線。由圖7可知，隨著小參數的增大，系統組合共振的振幅不變，但共振區相應減小。

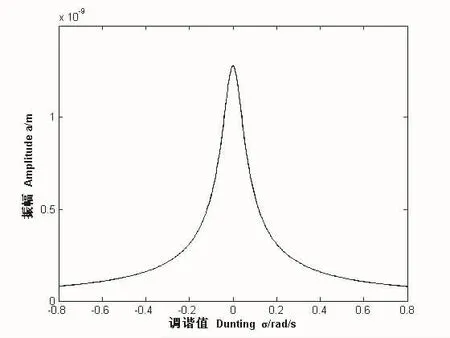
圖6 幅頻響應曲線（β）

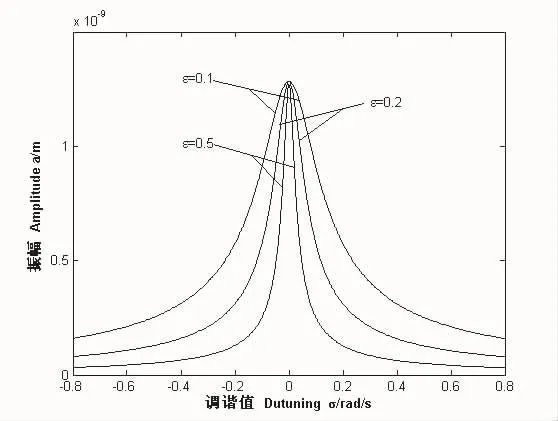
圖7 幅頻響應曲線（ε）

4 結論

應用常微分方程理論，將三自由度基礎結構耦合系統受地震激勵動力學方程，變換為單自由度受三頻激勵的杜芬方程。采用非線性振動的多尺度法，求得系統三頻率組合共振的一次近似響應曲線，分析了系統參數對共振響應曲線的影響。小參數變化會引起激勵幅值的變化，這是此種組合共振的特征。系統組合共振的振幅隨著地基土層厚度的增加而增加，隨著地基剪切波速的增加而減小，且這兩種地基參數對共振區的影響較明顯。這一點在基礎選址和工程動力學設計中要給予重視。

［1］ 張克緒，謝君裴．土動力學［M］．北京：地震出版社，1989：56－75．

［2］ Constantinou M C，Keneifati M．Dynamics of soilbase－isolated structure system［J］．Joural of Structural Engineering，1988，114（1）：211－221．

［3］ Stewart J，Fanves G．System identification for evaluating soil－structure interaction effects in buildings from strong motion recordings［J］．Earthquakes Engineering and Structure Dynamics，1998，27（8）：869－895．

［4］ 房營光．非線性地基－結構系統的地震共振突變分析［J］．巖石力學與工程學報，2004，23（9）：1509－1514．

［5］ 房營光，曹洪．地基－結構系統地震響應的突變模型分析［J］．巖土力學，2003，24（5）：729－732．

［6］ 許強，黃潤秋．地震作用下結構非線性響應的突變分析［J］．巖土工程學報，1997，19（4）：25－29．

［7］ Nayfeh A H，Mook D T．Nonlinear Oscillations［M］．New York：Wiley Interscience，1979：198－216．

［8］ 楊志安，席曉燕，李文蘭．彈性直桿在溫度場中的非線性振動與奇異性［J］．工程力學，2006，23（6）：50－53．．

［9］ 胡海巖．應用非線性動力學［M］．北京：航空工業出版社，2000：98－116．