超衍射成像中雙螺旋點擴展函數的三維定位精度*

陳鶴 于斌 陳丹妮 李恒 牛憨笨

(深圳大學光電工程學院,光電子器件與系統(教育部/廣東省)重點實驗室,深圳 518060)

(2013年3月7日收到;2013年3月29日收到修改稿)

1 引言

得一了種

近較是年大基來的于,發縮遠展小場有[1納].效米目激分前發辨最光熒為斑突光,出顯 通的微 過方成 直法像 接有技 減兩術 小種取點,擴展函數的半高寬來提高分辨率,包括受激輻射耗盡(stimulated emission depletion,STED)、基態耗盡(ground state depletion,GSD)、飽和結構激發顯微術(saturated pattern excitation microscopy,SPEM)等;另一種則是基于單分子定位技術,包括隨機光學重建顯微術(stochastic optical reconstruction microscopy,STORM)、光敏定位顯微術(photoactivated localization microscopy,PALM)及熒光PALM(fl uorescence photoactivation localization microscopy,fPALM)等.前者是利用受激態或基態耗盡的方式,壓縮熒光有效發射區域;后者則是利用熒光標記本身的開關效應,通過稀疏激發、分時成像、質心定位以及圖像合成來實現納米分辨成像,并已經實現20 nm的橫向空間分辨率成像.

然而,傳統的單分子定位方法只能對分子進行二維也就是橫向定位,但對于軸向分辨率并沒有提高.結合某些改進軸向分辨率的方法,如柱面鏡定位[2]、雙焦面探測[3]、雙螺旋點擴展函數法(double helix point spread function,DH-PSF)[4]以及熒光干涉法[5]等,能將軸向分辨率提高到50 nm的水平.其中,DH-PSF是通過特殊設計相位板,改變系統的點擴展函數形成雙螺旋的形式,并且旋轉的方向與熒光分子的軸向位置有關,從而獲得熒光分子的軸向定位.該方法具有相比其他方法更長的可探測焦深范圍,并且在整個成像深度內,點擴展函數的形狀近似不變,僅隨軸向位置發生旋轉,而不像其他方法需要通過精確形狀圖像比對來得到軸向位置,從而定位精度可以做得更高.

考慮到單分子定位超分辨方法中,定位精度直接決定了其極限分辨率,因此有必要對DH-PSF的三維定位精度進行詳細的分析.本文通過兩種方法來分析DH-PSF的三維定位精度：首先,基于費希爾信息量(Fisher information,FI)理論分析了DH-PSF的三維FI理論定位精度;此外,基于高斯擬合質心定位算法,利用誤差傳遞理論求得DH-PSF的三維模擬質心定位精度,并對二者進行了比較和分析.結果表明,在光子數大于1000的情況下,二者得到的定位精度接近.本文重點分析了光子數、背景噪聲、軸向位置對定位精度的影響,這將對于DH-PSF的三維定位實驗提供理論指導.

2 DH-PSF實現三維納米定位原理

DH-PSF實現三維納米定位是基于一種被稱為自成像的現象.DH-PSF是一種三維光學響應,具有隨離焦量不斷旋轉的圓形不對稱橫截面輪廓.實現DH-PSF的主要方法是通過位于Laguerre-Gauss(LG)模式平面上特定直線上的LG模式的線性疊加.LG光束模式的線性疊加構成自成像光束.LG光束模式為[6]

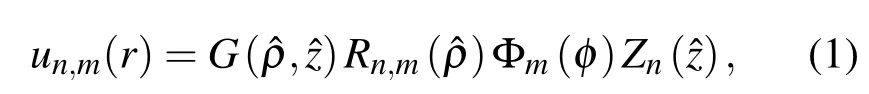
式中r=(ρ,φ,z)為空間點的柱坐標,ρ?=ρ/ω(z?)是高斯光斑的經向坐標,為束腰半徑,z?=z/z0縱向坐標,z0=πω02/λ為瑞利長度,un,m(r)的組成為

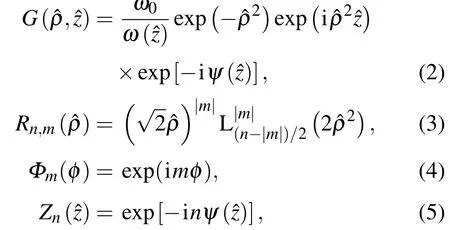
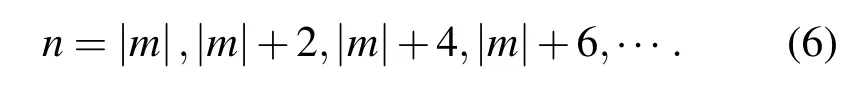
將(1,1),(3,5),(5,9),(7,13),(9,17)五個LG模式進行等權重疊加,形成一個新的光場分布函數,即雙螺旋旋轉光束(圖1(a)).基于LG函數的傅里葉變換不變特性,該函數如作為光學傳遞函數應用到光學成像系統中,光學系統的點擴展函數將變為DH-PSF,且隨離焦量變化而旋轉的速度與LG模式平面上所選取的直線斜率成正比,在聚焦區速度最大(圖1(c)).一個DH-PSF系統是在標準成像系統的傅里葉平面加入一個特殊設計的相位板,此相位板是其透射率函數在傅里葉變化的聚焦區形成雙螺旋的形式.更特別的是它展示了兩個圍繞著光軸旋轉的旁瓣,其中一個繞著光軸順時針旋轉,而另一個則是逆時針旋轉.用DH-PSF進行三維納米定位時,分子的橫向定位點通過兩個旁瓣的中點來估計,而其軸向位置則根據兩個旁瓣中心連線的旋轉角度(圖1(b))確定[7].

3 基于FI理論計算DH-PSF的三維定位精度

FI是一種測量隨機變量X與取決于X概率的未知參數θ的信息量.X的概率函數也就是θ的似然函數,記作 f(X,θ).似然函數的對數對θ的偏導數叫作得分函數.在特定的條件下,得分函數的一階矩為0,二階矩為FI,則FI表達式為

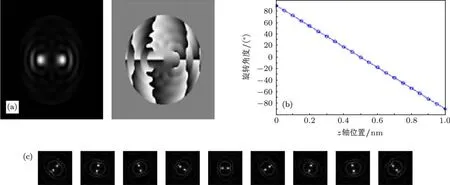
圖1 DH-PSF (a)DH-PSF的強度與相位分布;(b)DH-PSF兩個旁瓣的旋轉角度與Z軸位置的關系曲線圖舉例;(c)DH-PSF在不同軸向位置處的圖形

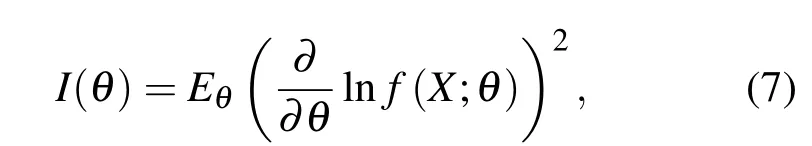
就基于DH-PSF的單分子定位而言,似然函數就是DH-PSF,感興趣的參量就是單分子的橫向和軸向位置根據Cramer-Rao不等式,一個未知參數θ的無偏估計值θ?的變化往往大于或者等于FI逆矩陣[8].

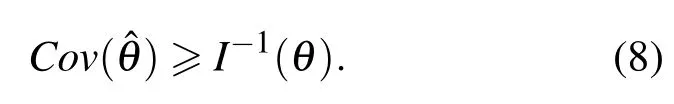
DH-PSF的Cramer-Rao邊界(Cramer-Rao bound,CRB)代表了無偏估計值的最小可能位置的估計方差,通過選擇適當的噪聲分布,可計算不同信噪比下的CRB.對于單分子的3D定位問題,3D定位精度的極限為FI逆矩陣的對角線元素的平方根,其計算如下[9]：

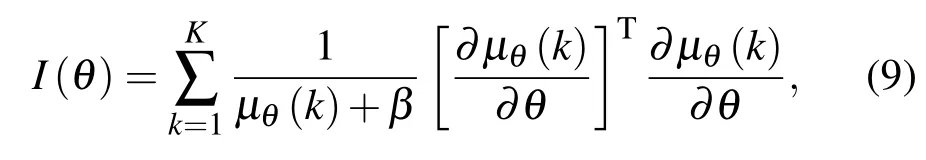
其中θ=(x0,y0,z0),μθ為PSF在每個像素點上的概率密度函數,β為每個像素點上的泊松背景噪聲,K為總的像素數.

則其光子受限系統中的CRB為

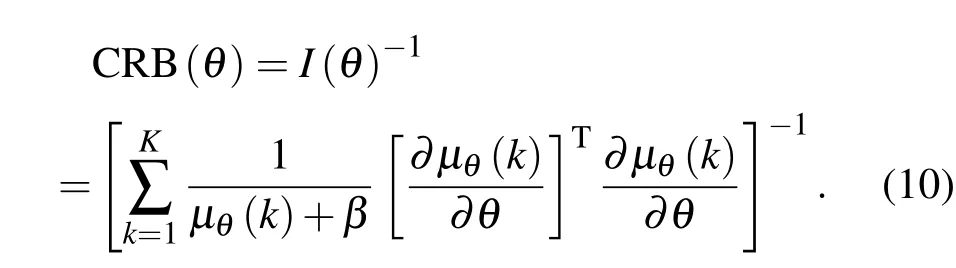
由前面可知3D的定位精度與CRB的平方根是一致的,所以光子受限系統中的三維定位精度表達式如下：

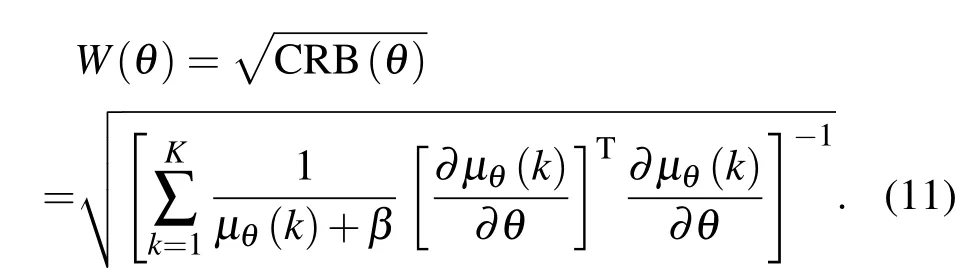
為了計算DH-PSF的FI矩陣,我們必須求解成像函數的PSF及其偏導數.在基于雙螺旋點擴展函數的熒光顯微系統中,位于點(0,0,z)處的熒光分子所成的像,即為系統的DH-PSF,其3D-PSF數學模型如下[10,11]：

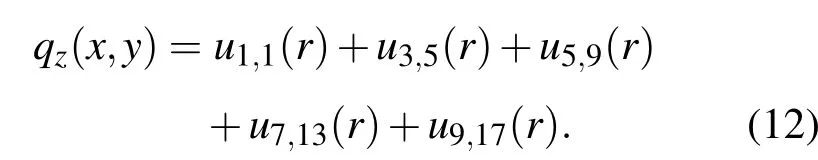
把qz(x,y)代入(9)—(12)式得：

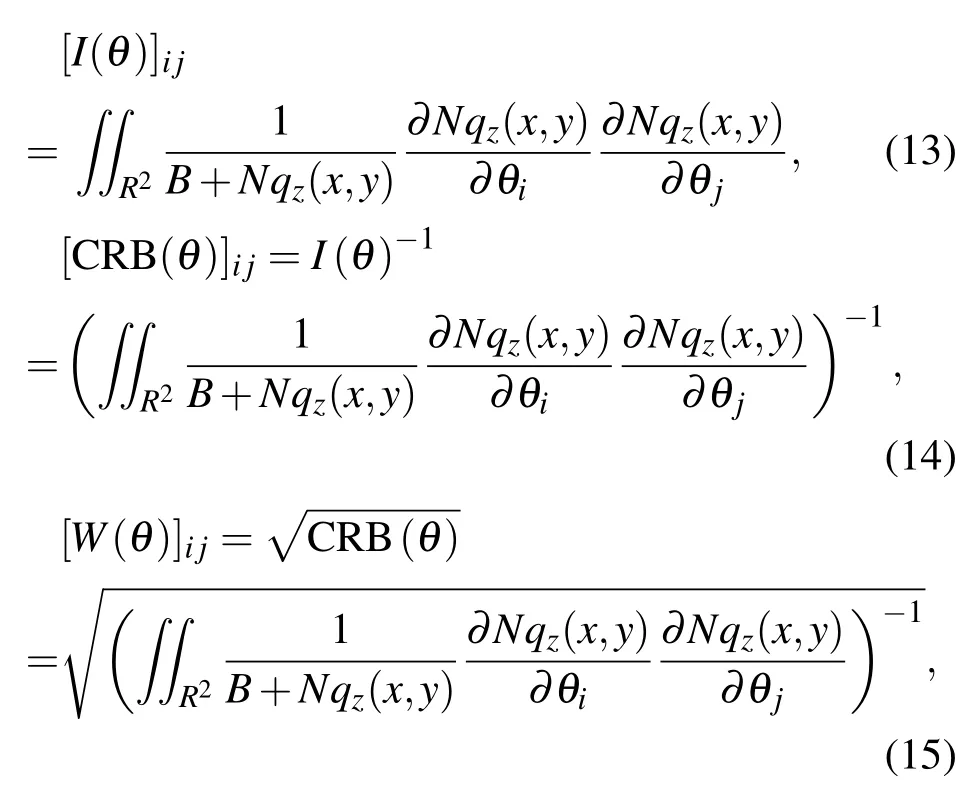
i,j=1,2,3;θ∈{x,y,z},N表示總光子數,B為背景噪聲.

為了計算DH-PSF的理論定位精度,我們重點分析了光子數、背景噪聲、軸向位置對其定位精度的影響.所有的理論定位精度的模擬計算均在Matlab編程環境下實現.模擬參數如下：熒光波長λ=670 nm,物鏡放大倍率M=100,數值孔徑N=1.4,探測器像元大小為16μm.通過探測光子數的不同,可以分別求出其不同的三維定位精度,如圖2(a)所示.由于定位精度與光子數的開方成反比,所以隨著光子數的增加,所求得的W(θ)值就越小,也就是其定位精度越高.如圖2(b)所示,光子數為1000時,通過所加背景噪聲的不同,可以分別求出其不同的三維定位精度.隨著背景噪聲的增加,定位點的分布就越寬,所求得的W(θ)值就越大,也就是其定位精度越低.光子數為1000和5000時,通過z的取值不同(-1—1μm),可分別求得各個位置處的三維定位精度,如圖2(c)—(e)所示.在x,y軸定位精度上,由于其橫向定位精度與光斑的大小有關,光斑越小其定位精度就越高.在不同的z軸位置上,最中間的光斑最小,旁邊的都隨著離焦而有所增大,所以在中點位置的定位精度最高,隨著中點依次降低;在z軸定位精度上,其定位精度不僅與光斑尺寸有關,還與兩個光斑之間的距離有關,距離越遠定位精度越高.離焦越遠,兩個點之間的距離越大,所以在中點位置的定位精度最低,隨著中點依次升高.通過對軸向及橫向定位精度隨分子所處離焦量的變化曲線可以看到,在焦點位置,橫向定位精度達到最高,而軸向定位精度最低.

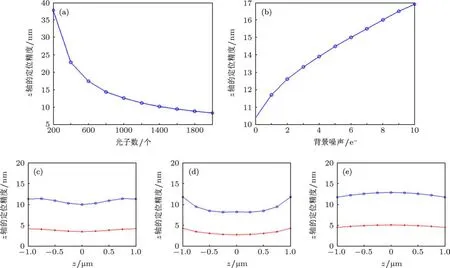
圖2 DH-PSF定位精度模擬圖 (a)不同光子數情況下的軸向定位精度;(b)不同背景噪聲的軸向定位精度;(c),(d),(e)不同位置處的x,y和z軸定位精度(藍色為光子數N=1000,紅色為光子數N=5000)

4 運用誤差傳遞定律計算DH-PSF的三維質心定位精度

DH-PSF的軸向質心定位精度是由兩個旁瓣相對于軸向距離的旋轉角來確定的,根據其產生原理,可知旋轉角θ為[12]

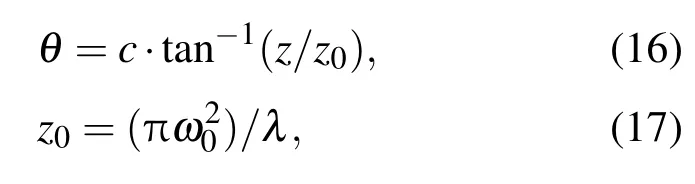
c為在LG模式平面上所取點的斜率,z0為瑞利長度,ω0為束腰半徑.由數學知識我們可知,兩個點相對于水平方向的夾角為

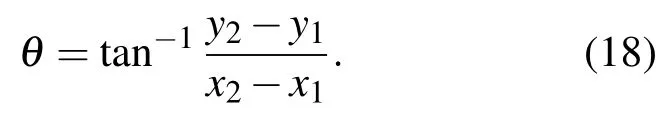
把(18)式代入(16)式可得：

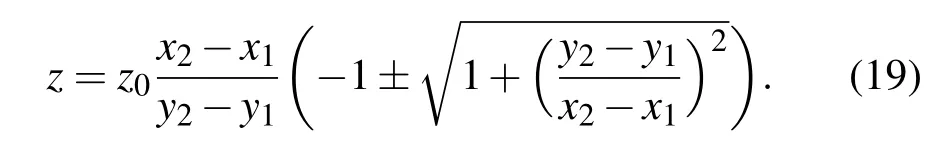
誤差傳遞函數定律為[13]

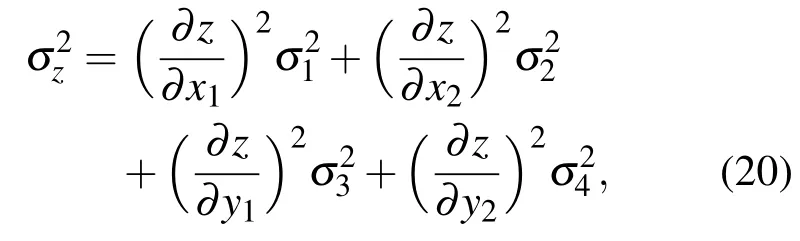
式中σ1(σ2,σ3,σ4)為x1(x2,y1,y2)的標準差,把(19)式代入(20)式則σz為DH-PSF的軸向定位精度.

下面,我們通過計算機進行DH-PSF定位精度的模擬,所有計算均在Matlab編程環境下實現[14].模擬參數如下：樣品尺度為12×12個像元,熒光波長λ=670 nm,物鏡放大倍率M=100,數值孔徑NA=1.4,探測器像元大小為16μm.如圖3(a)所示,源圖像的生成方法如下：首先,通過(1,1),(3,5),(5,9),(7,13),(9,17)五個LG模式疊加得到DH-PSF的圖像;然后,再加上泊松分布的光子散彈噪聲和高斯分布的背景噪聲,最終獲得用于定位的2000幅源圖像.模擬實驗中,背景噪聲均值為2e-/pixel.

圖像重構步驟如圖3(b)所示.首先,對上面的源圖像進行濾波降噪;再把圖像分成兩個區域,分別求得兩個區域的最大值的坐標,并作為高斯擬合的初值,用高斯擬合質心定位算法進行定位,獲得4000個定位點,求得這4000個定位點的標準差,代入(20)式即可求得其軸向的定位精度.

通過上面定位算法所求得的軸向質心定位精度與前面計算CRB所得出的FI理論定位精度比較,如圖4所示,藍色為計算CRB所得出的FI理論定位精度,紅色為質心定位算法所求定位精度.通過質心定位算法求得的定位精度比FI理論定位精度低(誤差數值高),且在光子數比較少的情況下差距比較大,但在光子數比較多時,兩個數值基本相同.

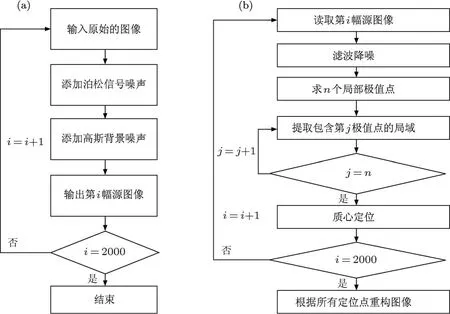
圖3 定位算法步驟原理圖 (a)源圖像的生成;(b)圖像的重構

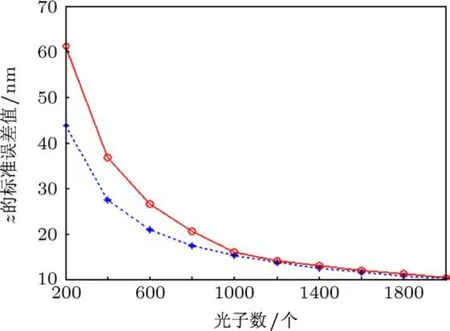
圖4 質心定位算法(紅色)所求得的軸向定位精度與計算CRB(藍色)所得出的FI理論定位精度比較

5 總結與討論

通過對DH-PSFFI矩陣的計算,求得其CRB值,表示了它的FI理論三維定位精度.同樣,根據質心定位算法也求出了其定位精度.兩者相比較可知,運用質心定位精度算法求出的定位精度要比直接運用公式計算CRB所得的FI理論定位精度要低;但是,在光子數大于1000的條件下,二者的差別還是比較小的,基本上一致.由于在光子數少的情況下,信噪比較差,運用高斯擬合質心定位時,造成對質心位置的定位偏差過大,從而造成質心定位精度算法求出的定位精度標準誤差增大,即定位精度降低;而在光子數多的情況下,噪聲對質心位置定位的偏差較小,因此二者之間的定位精度基本一致.

[1]Chen D N,Liu L,Yu B,Niu H B 2010 Acta Phys.Sin.59 6948(in Chinese)[陳丹妮,劉磊,于斌,牛憨笨2010物理學報59 6948]

[2]Holtzer L,Meckel T,Schmidt T 2007 Appl.Phys.Lett.90 053902

[3]Toprak E,Balci H,Blehm B H,Selvin PR 2007 Nano Lett.7 2043

[4]Pavani SRP,Thompson M A,Biteen JS,Lord SJ,Liu N,Twieg RJ,Piestun R,Moerner WE 2009 PNAS106 2995

[5]Shtengel G,Galbraith J A,Galbraith C G,Lippincott-Schwartz J,Gillette J M,Manley S,Sougrat R,Waterman C M,Kanchanawong P,Davidson M W,Fetter RD,Hess H F 2009 PNAS106 3125

[6]Piestun R,Schechner Y Y,Shamir J2000 JOSA A 17 294

[7]Pavani S R P,Greengard A,Piestun R 2009 Appl.Phys.Lett.95 021103

[8]Thompson M A,Lew M D,Badieirostami M,Moerner WE 2010 Nano Lett.10 211

[9]Ober RJ,Ram S,Ward ES 2004 Biophys.J.86 1185

[10]Badieirostami M,Lew M D,Thompson M A,Moerner WE 2010 Appl.Phys.Lett.97 161103

[11]Ram S,Prabhat P,Chao J,Ward E S,Ober R J 2008 Biophys.J.95 6025

[12]Khonina SN,Kotlyar V V,Soifer V A,Honkanen M,Lautanen J,Turunen J1999 J.Mod.Opt.46 227

[13]Liu Z M 1981 Error and Interpretation of Data(Beijing：Atomic Energy Press)p21(in Chinese)[劉智敏1981誤差與數據處理(北京：原子能出版社)第21頁]

[14]Chen D N 2010 Ph.D.Dissertation(Wuhan：Huazhong University Of Science And Technology)(in Chinese)[陳丹妮2010博士學位論文(武漢：華中科技大學)]