Bargmann約束下一個新的有限維可積系統

李章，張金順

（華僑大學 數學科學學院，福建 泉州362021）

有限維可積系統一直是人們感興趣的研究課題.特征值問題的非線性化方法溝通了有限維可積系統與無限維可積系統之間的聯系，是構造有限維可積系統的重要途徑［1-4］.本文通過引入映射，導出遞推算子和孤立子方程族.在Bargmann約束下，將Lax非線性化為有限維Hamilton系統，并利用母函數方法導出對合的守恒積分.

1 Lenard算子與對孤子方程族

考慮2×2特征值問題，即

定義一個線性映射［5］σλ∶C3→sl（2，C），即

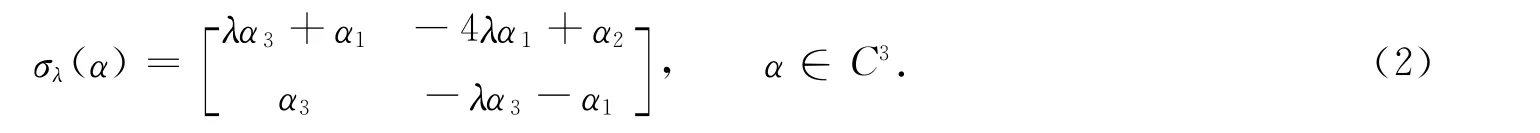
則U＝σλ（u，v，1）T.

令V＝σλ（G），G∈C3，則

式（3）中：K，J為Lenard的算子對，即

命題1 矩陣V＝σλ（G）滿足Lax方程Vx-［U，V］＝0的充分必要條件是：Kgj＝Jgj+1，Jg-1＝0，其中：j＝-1，0，1，….

利用命題1，可以計算出Lenard序列｛gj｝和向量場｛Xj｝，即

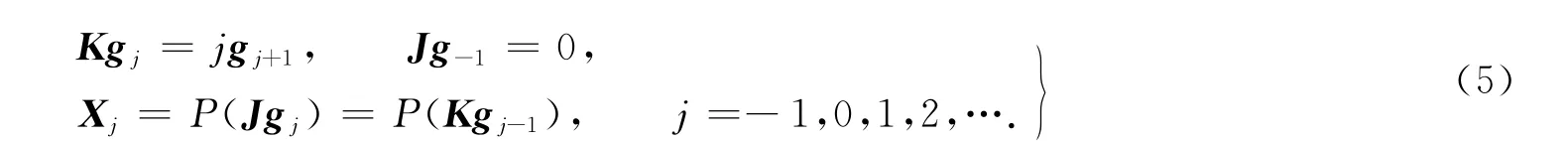
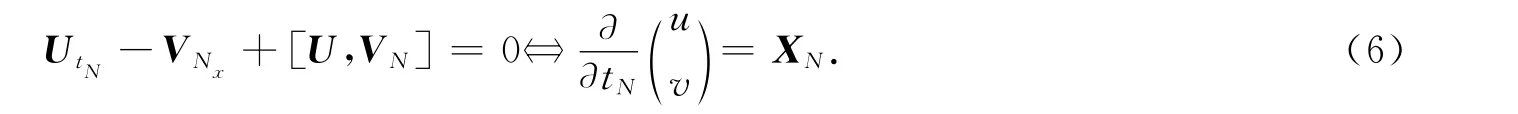
特別地，當N＝1，2時，由式（8），分別可得孤立子方程為

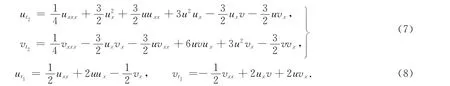
Lax對為

2 Bargmann系統

令φ＝（φ1，φ2）T是方程（1）的一個解，定義一個映射［5］τλ∶C2→C3為

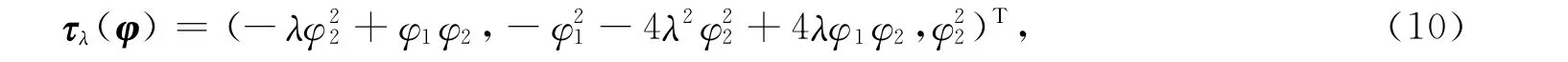
則τλ（φ）滿足方程

設λj（j＝1，2，…，N）為方程（1）的N個互異特征值，對應的特征函數滿足方程

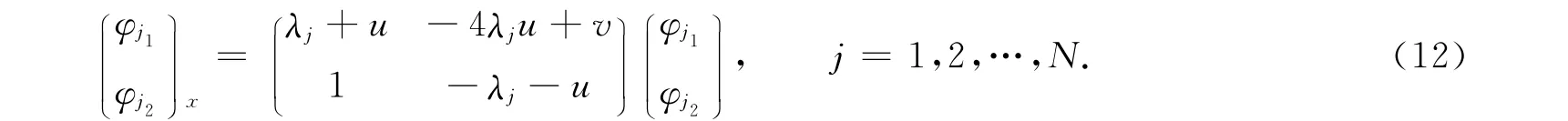
其映射定義為

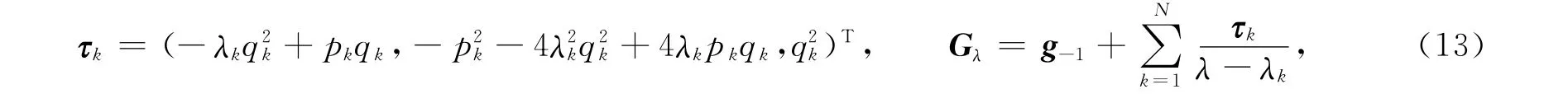
式（13）中：qk＝φk2，pk＝φk1.由式（13），可得到一個Lax陣，即

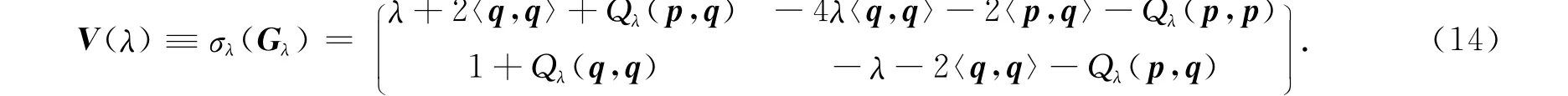
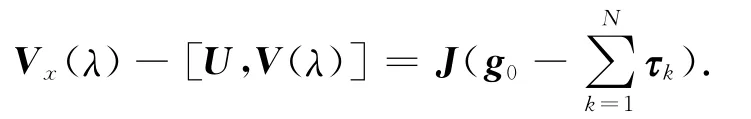
證明 通過式（3），（11）即可證明.

引入Bargmann約束

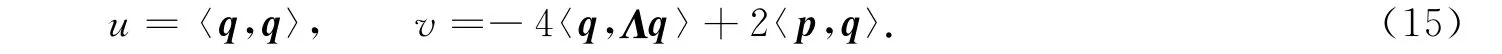
式（15）中：p≡（p1，…，pN）T；q≡（q1，…，qN）T；Λ＝diag（λ1，…，λN）.

則特征值問題（1）被非線性化為N維Hamilton系統，即

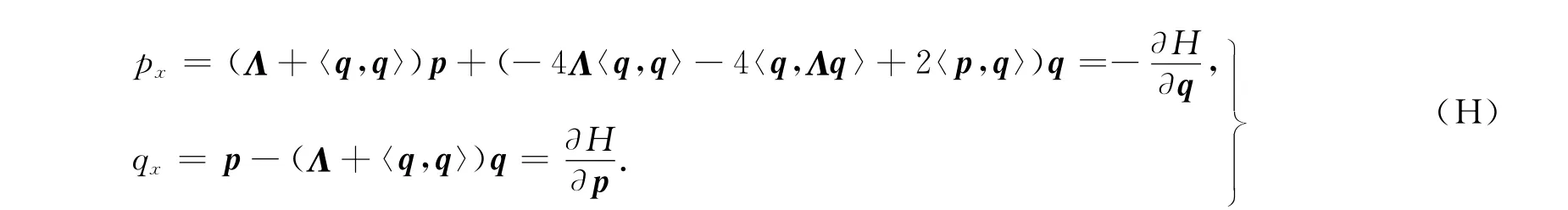
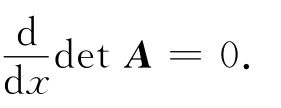
證明 利用A，B∈sl（2，C）的特殊性質，及Lax方程Ax＝［A，B］，直接計算可證.

將母函數F（λ）展開為λ的洛朗級數，得到

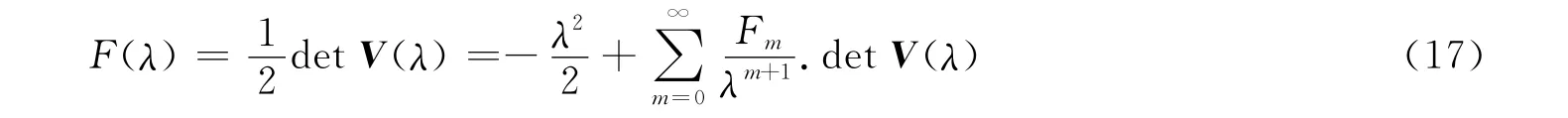
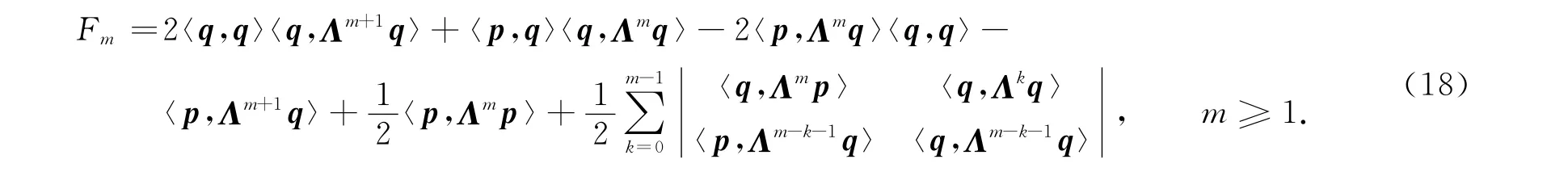
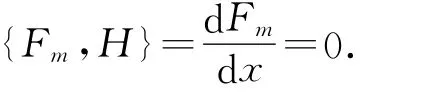
［1］ 曹策問.AKNS族的Lax方程組的非線性化［J］.中國科學：A輯，1989，32（7）：701-707.

［2］ 杜殿樓.產生有限維可積系統的一個新途徑［J］.鄭州大學學報：自然科學版，1997，29（1）：1-7.

［3］ CAO Ce-wen，GENG Xian-guo.Classical integrable systems generated through nonlinearization of eigenvalue problems Nonlinear［C］∥Research Reports in Physics.Berlin：Springer，1989：68-78.

［4］ CAO Ce-wen，WU Yong-tang，GENG Xian-guo.Relation between the Kadometsev-Petviashvili equation and the confocal involutive system［J］.J Math Phys，1998，40（8）：3948-3970.

［5］ WU Yong-tang，ZHANG Jin-shun.Quasi-periodic solution of a new （2+1）-dimensional coupled soliton equation［J］.J Phys A：Math Gen，2001，34（1）：193-210.