海洋管道單點提放的若干數學模型研究

曾霞光，段夢蘭，陳景皓

(中國石油大學(北京)機械與儲運工程學院，北京 102249)

隨著中國深海油氣開發的進程，中國必須掌握深水管道鋪設和安裝的分析設計技術。深水海洋油氣開發中，主要的鋪管安裝方式有S型鋪設，J型鋪設等。鋪管和安裝作業中，回收和棄置管道操作非常普遍。在這些作業過程中，管道的軸力，彎矩，應力，應變等需要控制在一定的范圍內以保證管道完好，因此海洋管道鋪設和收棄作業方案，尤其是船舶位置移動設計和纜繩的收放速度非常重要。為了進行設計分析，需要建立海洋管道的收棄作業過程分析模型和方法。

鋪管作業可以看作棄管作業的前期工作或者收管作業的后期工作，因此用于分析的力學模型與收棄管分析模型相同。棄置時海洋管道通常將脫離托管架或其他支撐結構，A＆R絞車的鋼繩通過海洋管道封頭將管道從海面緩慢下放到海底，回收時A＆R絞車的鋼繩通過海洋管道封頭將管道從海底緩慢拉升到海面上，此過程被稱為海洋管道的單點提放。在這個往復過程中，管道經歷了一個大變形和小變形相互轉化的變形過程。

1 控制微分方程

海洋管道從海底提升到海面或者從海面下放到海底，這兩個物理過程是互逆的，可以用同一個數學模型進行描述。在管道提放作業時通常要求海洋環境平穩，管道提升或者下放速度緩慢，因此可把問題處理成靜態問題。另外可認為海底為剛性水平面［1］，海洋管道由各向同性材料組成，且提升和下放過程中始終處于彈性狀態。在上述條件下，不考慮海水流動效應，取懸空管段進行研究，如圖1所示。以懸空管道與海床的接觸點(觸地點)為原點o，建立笛卡爾坐標系。再沿管線建立自然坐標系，顯然該管線上的物理量均為管線弧長的單變量函數。令管道與水平方向的夾角為θ，長度為L，材料彈性模量為E，截面慣性矩為I，水中的單位線重為w，上端點受拉力T0作用，與水平方向成夾角θ0，管線原點處橫截面的水平力為H0，鉛垂力為V0。其中鉛垂力V0的可能來源有且僅有兩個，一個是左邊管道對其剪力，另一個是剛性接觸海床對其向上的支撐力。由于通常認為左邊管道沒有彎曲變形，其彎矩為零，因此其相互剪力也為零，否則左邊管道必然彎曲。由此可知原點處的鉛垂力就是剛性海床對其向上的支撐力。

根據文獻［2-5］，如圖1所示的海管提放問題可以用如下微分方程描述:

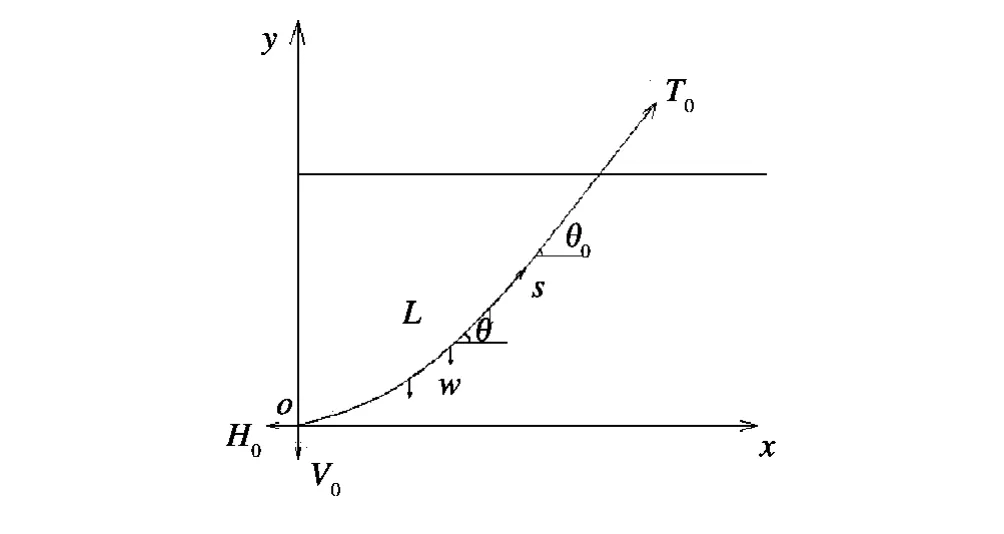
圖1 管道單點提放力學模型Fig.1 Mechanical model of pipe lifting or lowering by one point

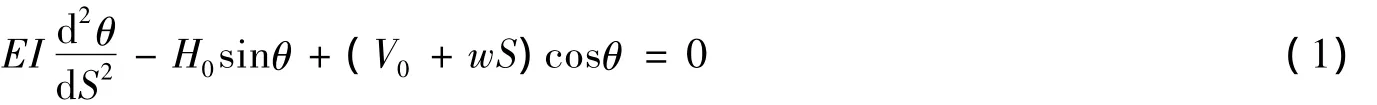
根據水平和垂直方向上力的平衡有:

將式(2)、(3)代入方程(1)得:

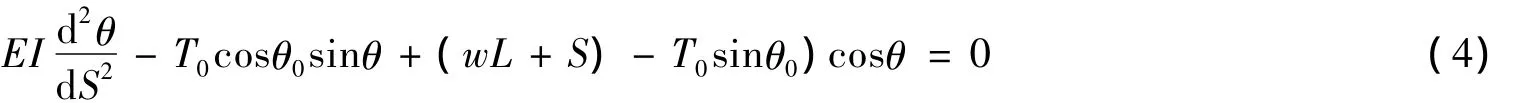
根據文獻［6］，該問題也可以用以下控制微分方程組描述:

用這兩種微分方程對管道收放問題進行分析，結果差異何在?這兩種控制微分方程是否都能很好地描述海洋管道的提放過程?哪種微分方程更好地描述海洋管道的提放過程?為了回答上述及相關問題，將以兩種微分方程為核心建立海洋管道提放過程的三個分析模型，并借助數值計算方法分別進行求解，然后對計算結果進行分析。

2 邊界條件

分析海洋管道提放過程中邊界處的形態和受力情況，通常認為有如下邊界條件［3，5-7］:

觸地點處:撓度 y(0)=0，轉角 θ(0)=0，水平力 H0=T0cosθ0，彎矩 M(0)=0。

上部端點處:彎矩M(L)=0，拉力為T0。

3 懸空管道長度

懸空管道長度L是求解本問題的關鍵參數，不能預先確定。文獻［1］認為剛性海床情況下提起段長度等于2倍的提升力除以管道線重，文獻［2-3］根據幾何條件確定懸空管道長度，而文獻［5-8］都用各自的迭代方法確定該參數。與這些方法不同，將根據力學原理提供一個新的確定懸空管道長度的公式。

考慮懸空管道的外力對管道上部端點的彎矩，根據彎矩平衡原理有:

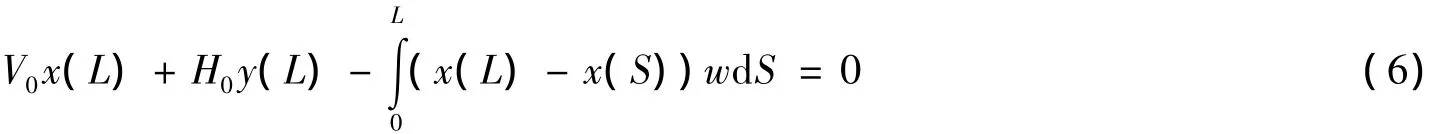
將式(2)、(3)代入式(6)得:

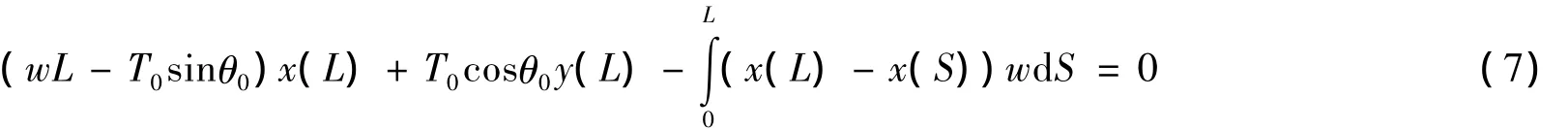
式(7)中只有一個獨立未知量變量L，L一旦確定，x(L)，y(L)和x(S)就隨之確定，因此可以求解該方程來確定懸空管道長度。求解方法是迭代法，思路為不斷假設一個懸空管道長度L，求解以式(4)或式(5)為控制微分方程的定解問題得到管道形態，直到下式成立:

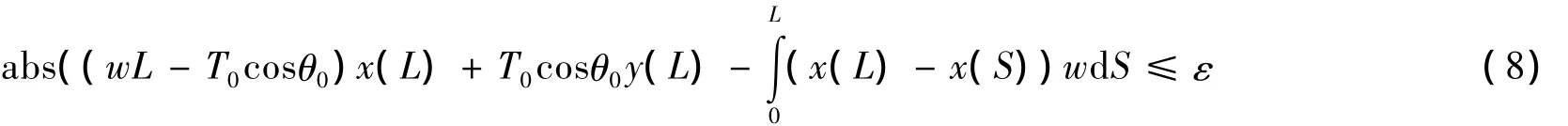
此時即可認為該長度就是管道懸空長度，其中ε為迭代計算誤差限。

4 數學模型

取微分方程(4)，選擇如下邊界條件:觸地點處的轉角為零，上部端點處的彎矩為零，再結合式(7)，得到分析模型1，即:

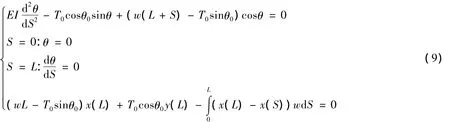
取微分方程(4)，選擇如下邊界條件:觸地點和上部端點處的彎矩都為零，再結合式(7)，得到分析模型2，即:

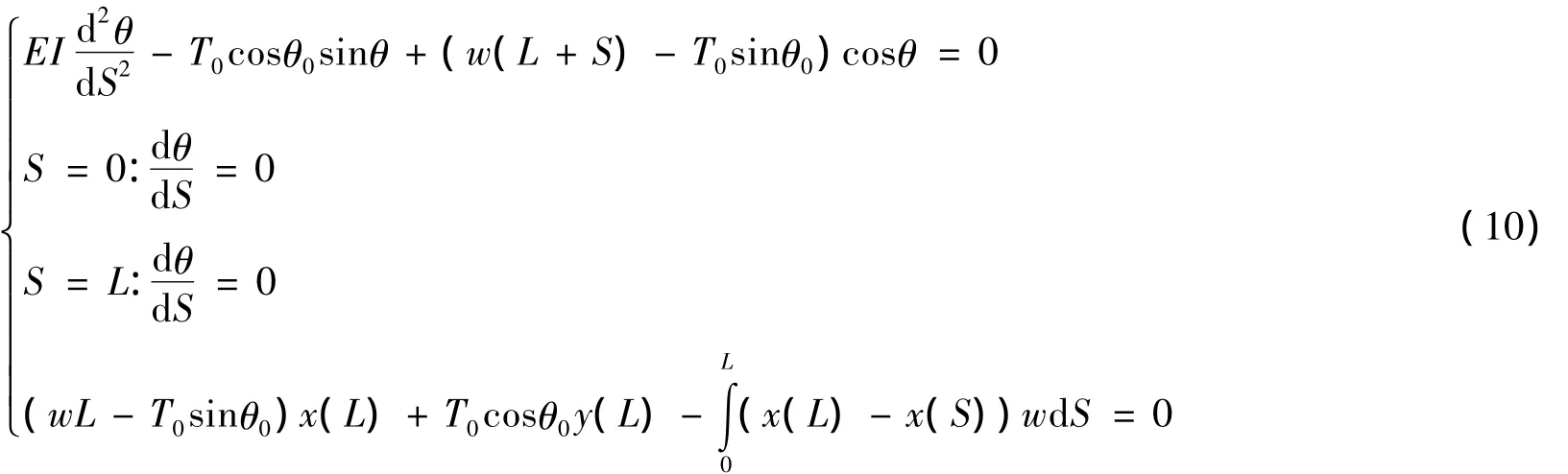
取微分方程組(5)，選擇如下邊界條件:觸地點處的轉角為零，彎矩為零，水平力為T0cosθ0，上部端點處的彎矩為零，再結合式(7)，得到分析模型3，即:

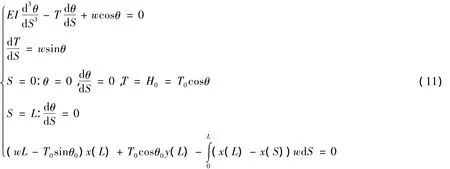
5 數值求解算例及結果分析

模型1和模型2的未知函數是θ(S)，模型3的未知函數是θ(S)和T(S)，由于上述微分方程均是高度非線性方程，無法得到其解析形式的解。為了分析這些模型的差異，并找出準確描述海洋管道提放物理過程的數學模型，下面對它們進行數值求解。

采用MATLAB作為求解環境，利用其中的內置函數bvp4c［9］求解如表1、2所示的一組具體參數對應的分析模型1、2和3，計算結果如圖2所示。

圖2 不同拉力作用時管道的轉角、形態和彎矩Fig.2 Angle，configuration and bending moment of pipe loading under different tension

從計算結果圖2中可以發現以下主要特點:

1)模型3確定的懸空管道長度在三個模型中是最大的，模型2確定的懸空管道長度最小;

2)模型1的彎矩極值在三個模型中是最大的，發生在觸地點處，模型2的彎矩極值總是最小，模型2和3的彎矩極值都不發生在觸地點處;

3)彎矩極值隨著懸空管道長度的變化而變化，其先隨懸空管道長度增加而增加，之后隨懸空管道長度增加而減小，最大值發生在懸空管道約100 m處;

4)隨著載荷增大三個模型的解越來越接近，在懸空管道長度小于1 000 m時，三個模型的轉角、形態和彎矩的結果差別較大，且長度越小差別越大。在懸空管道長度大于1 000 m時，模型2和模型3的轉角、形態和彎矩的計算結果幾乎相同，但是模型1的結果與其它兩個模型在彎矩的極值及其發生位置存在較大差異;

5)從圖2(a)～(d)中可以清楚看出，模型1的彎矩極值發生在觸地點，這與實際情況矛盾，而模型2在觸地點的轉角值也與該問題的邊界條件矛盾。

表1 材料幾何參數Tab.1 Geometrical and material parameters

表2 載荷參數Tab.2 Loading parameters

根據計算結果的特點，可以初步判定描述海洋管道提放全程的數學模型應該采用分析模型3。為了進一步證實該模型的正確性，作者以分析模型3為理論模型，編寫開發了海洋管道提放靜力學分析軟件DRICAS，采用上文中的管道材料幾何參數，重新計算了如表3所示載荷情況下的管道形態。

表3 載荷參數Tab.3 Loading parameters

將其形態計算結果與專業海洋工程有限元分析軟件OrcaFlex的計算結果進行對比，可以看到兩者的計算結果在各個載荷情況下都是一致的，如圖3所示。這進一步證實了模型3的正確性。

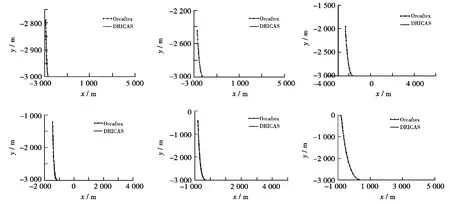
圖3 DRICAS和OcraFlex形態結果對比Fig.3 Configuration results comparison between DRICA and OcraFlex

6 結語

通過三個模型的數值求解和分析表明:

1)對海洋管道緩慢單點提放進行全程分析宜采用模型3，它能準確描述管道提放的完整過程;其中該問題的邊界條件是觸地點處水平轉角為零，彎矩為零，受到提升載荷水平分量大小的拉力，上部端點處彎矩為零;另外懸空管道長度可以根據彎矩平衡原理確定。

2)因為彎矩極值位置不合理，模型1不能準確描述海洋管道單點提放過程并用于管道的力學分析。

3)懸空管道長度小于900 m時，模型2不能準確描述海洋管道單點提放過程;懸空管道長度大于1 000 m時，模型2與模型3計算結果的相對誤差很小，且懸空管道越長相對誤差越小，因此在懸空管道長度大于1 000 m時可用模型2代替模型3，從而減少計算機數值計算時間。

4)彎矩極值隨著懸空管道長度變化而變化，其先隨著懸空管道長度增加而增加，之后隨著懸空管道長度增加而減小，最大值往往發生在管道提升過程的中前期或者下放過程的中后期。

［1］ 邢靜忠.海底管道離地點的接觸條件探討［J］.力學與實踐，2005，27(5):57-60.

［2］ 宋甲宗，戴英杰.海洋管道鋪設時的二維靜力分析［J］.大連理工大學學報，1999，39(1):91-94.

［3］ 戴英杰，宋甲宗，馮 剛.海底管道收棄管作業分析［J］.海洋工程，2000，18(3):75-78.

［4］ 邢靜忠，柳春圖，曾曉輝.海洋石油管道單點提升分析［J］.海洋工程，2002，20(3):29-33.

［5］ 曾曉輝，柳春圖，邢靜忠.海底管道鋪設的力學分析［J］.力學與實踐，2000，24(2):19-21.

［6］ Charles P.Sparks.Fundamentals of Marine Riser Mechanics［M］.Tulsa，Oklahoma:PennWell，2007:254-256.

［7］ 詹 侃，陸仁華.海底管道在鋪設過程中的二維靜態分析［J］.海洋工程，1991，9(4):14-20.

［8］ 帥 健，呂英民，張進國.用動坐標迭代法分析海洋管道敷設時的應力［J］.油氣儲運，1996，15(10):21-24.

［9］ Shampine L F，Gladwell I，Thompson S.Solving ODEs with MATLAB［M］.New York:Cambridge University Press，2003:133-211.