一種相控陣雷達數據處理中的雜波抑制方法

熊美英，陳 靜

（船舶重工集團公司723所，揚州225001）

0 引 言

現代雷達已采用先進的信號處理技術，運用了很多對雜波抑制的手段，如動目標顯示（MTI）、動目標檢測（MTD）、恒虛警率（CFAR）等，能夠有效地抑制虛警雜波，保持適當的檢測能力；但在氣象條件惡劣、地勢地形復雜的工作環境下，仍然會出現較高的雜波剩余現象［1］。這些剩余雜波增加了數據處理的運算量和存儲量，產生的虛假點跡干擾了真實目標的航跡起始，增加了監控區域內航跡相關的復雜度，在相控陣雷達體系中對自動轉入跟蹤任務的虛假航跡還會占用系統調度資源，干擾作戰決策，嚴重影響對正常目標的探測。因此，在進行常規的數據處理前，預先對回波信號進行一系列的雜波抑制處理，盡可能減少雜波對數據處理的影響，具有重要的實際意義。

1 雜波特性分析

雷達雜波種類復雜繁多，對檢測能力影響較大的主要有地雜波和海雜波。地雜波是一種面雜波，它的平均回波功率為：

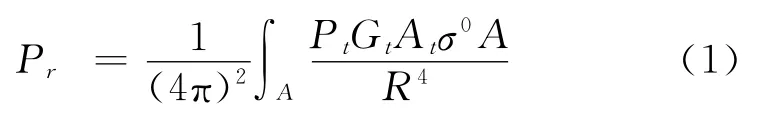
式中：Pr為接收功率；Pt為發射功率；Gt為發射天線增益；At為接收天線面積；R為距離；A為雷達天線的照射區域，σ0為地面散射系數。

發射波束覆蓋雜波區面積越大和后向反射系數越大，地雜波越強。地雜波的隨機起伏特性可以用概率密度分布函數和功率譜來表示，地雜波的起伏特性符合高斯分布，其高斯概率密度函數為：

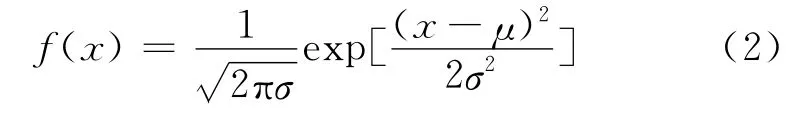
式中：μ為x的均值；σ2為x的方差。

地雜波的幅度符合瑞利分布，其瑞利分布的概率密度函數為：

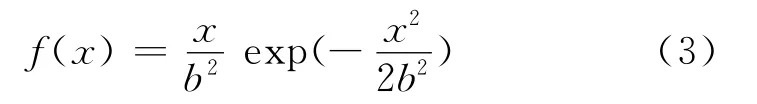
式中：b為瑞利系數，瑞利分布的均值μ和方差σ2分別為：

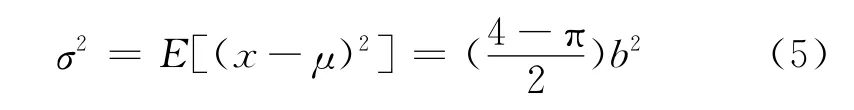
海雜波概率也可以用高斯分布來表示，其幅度概率密度分布也符合瑞利分布，但它受到風速、風向、洋流、水溫等海面狀態因素的影響而更為復雜，其概率分布時常會偏離高斯分布，有時需要采用更多的非高斯模型來分析，如對數正態分布、韋布爾分布和K分布等模型。

2 數據處理中雜波抑制

盡管在數據處理階段對雜波的抑制可利用的信息不如信號處理多，實時性不如信號處理強，但是通過對雜波特性的分析、回波信息的積累、比較及綜合判斷，也可以有效地濾除雜波信號。分析某型相控陣雷達真實發射狀態下的信號處理輸出回波信息，嘗試在數據處理中做了以下改進。

2.1 單波束內雜波濾除

每次收到來自信號處理的搜索波束數據時，對每個距離單元上過門限數據進行第1次雜波濾除。采集數據如表1所示，該數據為一個發射波束指向，方位上固定間隔的相鄰四接收波束連續距離單元上，過門限回波信號幅值和跨距離寬度。

表1 回波信號幅值和跨距離寬度

回波信號幅值反映目標回波的能量，回波跨距離寬度是指回波模擬信號經過采樣量化和信號處理幅度檢測后占據的連續距離單元個數。分析數據發現雜波和真實目標的回波信號在幅度和跨距離寬度上都有所區別，利用這個特征設置門限，剔除一部分雜波。通過數據統計發現，真實目標回波跨距離寬度一般都占據連續2個距離單元以上，所以可以將回波跨距離寬度設置為2，則表1中209、273、282的距離單元上孤立的回波被當作雜波濾除掉。接下來，對于連續占據2個距離單元的回波加設幅度門限，根據距離遠近調整不同幅度門限值，幅度低于門限值的點跡予以剔除。幅度門限值設置的基本依據是雷達方程［2］和平面相控陣天線方向圖函數［3］，分別見公式（6）和公式（7）：

式中：Pr為接收功率；Pt為發射功率；Gt為發射增益；Gr為接收增益；σ為目標RCS；λ為當前發射頻率頻點折算的波長；Ft為發射方向圖；Fr為接收方向圖；R為目標距離。

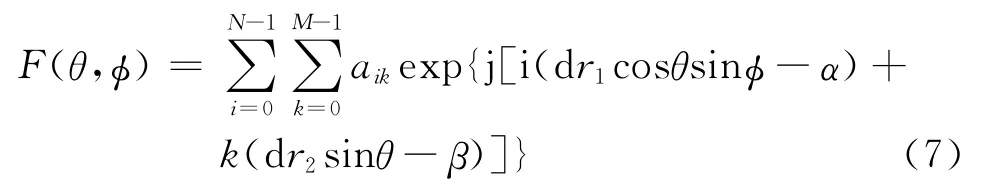
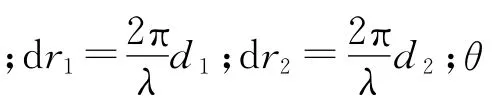
公式（6）、（7）中各項根據雷達的實際參數進行設置，幅度門限值即為接收功率的開平方，依據雷達各項參數設置幅度門限后，表1中距離單元為425、426的回波被排除。由于該方法計算量較大，考慮到數據處理的實時性要求，可以預先裝訂好雷達參數和關注目標特性，將幅度門限按照距離制成表格文件直接調用。

此外，數據處理中還可以針對每個回波的MTD通道號來進行雜波抑制，可以將徑向速度在零附近的回波數據剔除。

2.2 全掃描區域雜波圖門限比較

對于已經進行過單波束雜波濾除的數據，再進行一次全掃描區域的雜波圖門限比較，只有高于門限的回波才會進行數據處理。全掃描區域雜波圖是掃描范圍內按方位－距離單元分布的回波強度圖。方位－距離單元的劃分方法［4］如圖1所示，陰影部分為1個方位－距離單元。

1個方位－距離單元包括多個接收波束的連續幾個距離單元，將其中的回波幅度信息進行平均，得到幅度均值，每次掃描后得到的均值通過公式（3）進行迭代，即可獲得雜波圖中方位－距離單元上的雜波均值［4］：

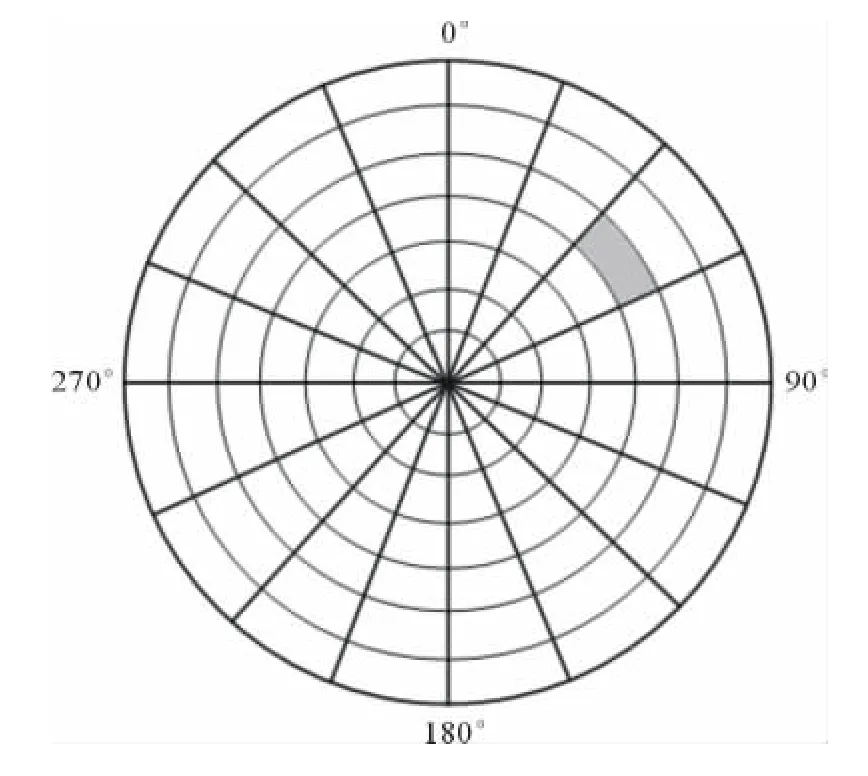
圖1 方位－距離單元的劃分方法

式中：n、m分別為方位、距離單元索引；l為天線掃描周期數；ω為濾波系數，一般取經驗值0.125。

由于雜波影響最嚴重的一般為低仰角，所以全掃描區域雜波圖采用了低仰角的掃描層數據進行更新，對雜波干擾嚴重的低仰角數據才進行雜波圖門限比對。對于快速目標（如飛機、導彈等），從一次掃描到下一次掃描一般移動幾個距離單元，所以雜波圖對運動目標影響不大。

2.3 雜波圖的空間重定位

空間雜波圖方位－距離單元的劃分建立在絕對坐標系的劃分方法上，所以需要分析雷達載體處于運動狀態時對建立的雜波圖的影響和解決辦法。在平臺運動方向的坐標系中，雜波圖的空間重定位可以通過公式（9）、（10）進行計算：

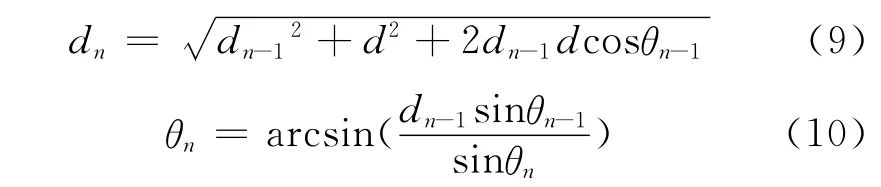
式中：d為雷達載體從周期Tn－1到Tn之間的運動距離；dn－1、θn－1分別為雜波圖中的任意一個方位－距離單元在Tn－1時刻的距離、方位；dn、θn分別為該方位－距離單元在Tn時刻的距離、方位。

當雷達載體位置發生變化時，對雜波圖中的每個方位－距離單元進行上述的空間重定位的計算量是非常大，工程應用中難以實現。因此，需要針對公式進行進一步簡化處理。首先，d遠小于dn－1、dn，可以將式（9）簡化為：

此外，在雜波圖的建立過程中，迭代周期內方位－距離單元還沒有形成一個比較可靠的閥值，可以粗略地在距離向做歸一化處理。通過事先做好方位－距離變化的對應表格，在實際工作中直接查表計算由于雷達載體運動造成的空間重定位，減少了復雜三角運算的計算量，能更準確實時地更新雜波圖數據。

3 雜波抑制效果比對

選取1組真實發射數據，搜索區域為法線方向（－30°，30°），掃描周期為1s，累計100個周期，統計結果如表2所示，顯示效果如圖2、圖3所示。

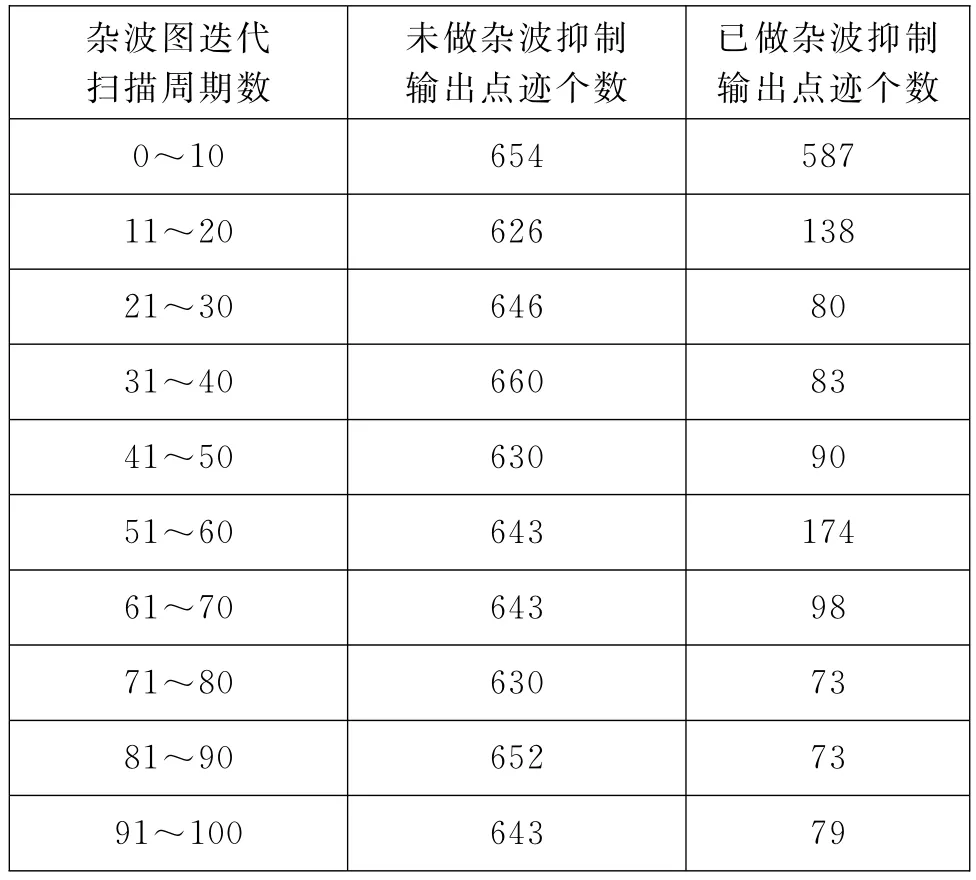
表2 雜波圖迭代數據

圖2為未做雜波抑制處理的數據處理結果顯示，每10個周期累計點跡數在600以上，100個掃描周期內虛警航跡數15條，受雜波點影響，真實目標航跡無法起始，而且由于單個波束點跡處理能力飽和，造成距離較遠的回波無法得到處理。

圖3為已做雜波抑制處理的數據處理結果顯示，剛開始10個周期內的累計點跡數在500以上，經過雜波抑制后，10個周期內的點跡累計數基本降到100以內，并且在100個掃描周期內，虛警航跡0條，真實航跡1條，該目標航速在60m／s，表明運用雜波抑制處理后，較慢速的真實目標回波并沒有被抑制掉，因此該抑制方法對運動目標的影響不大。此外由于雜波抑制后，單波束的點跡處理負擔減弱，遠距離的回波也能被處理為點跡輸出，保證了設備發現目標的能力范圍。

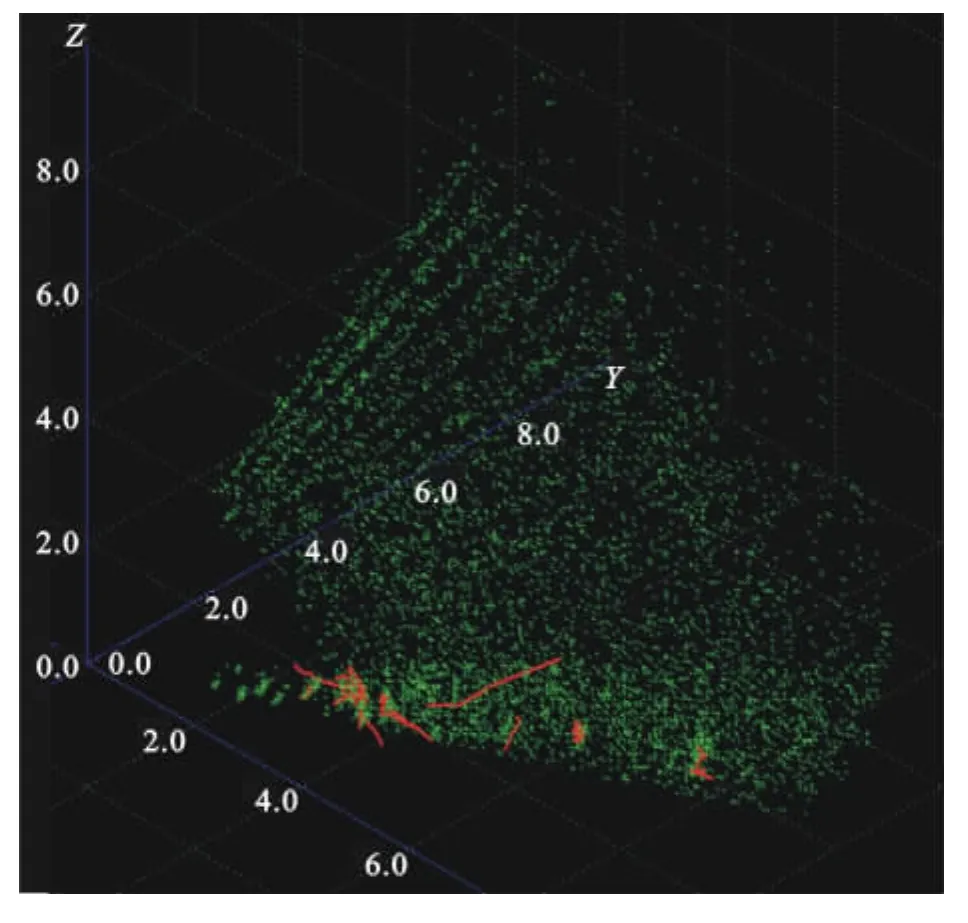
圖2 未做雜波抑制數據處理結果顯示

經過比對，上述方法對雜波抑制效果比較明顯。雜波抑制在數據處理階段的運用比較靈活，可以針對某個區域，可以選擇做哪種抑制處理，可以選擇抑制參數大小，這些都可以隨著現場雜波環境和設備關注目標類型進行選擇和調整，有效防止了真實目標丟失現象。

4 結束語

本文介紹了相控陣雷達數據處理中一種雜波抑制的方法，通過試驗數據效果比對，該方法對雜波的抑制作用明顯，但仍然存在雜波剩余，需要進一步對雜波特性進行分析，使得雷達性能獲得更好的改善。

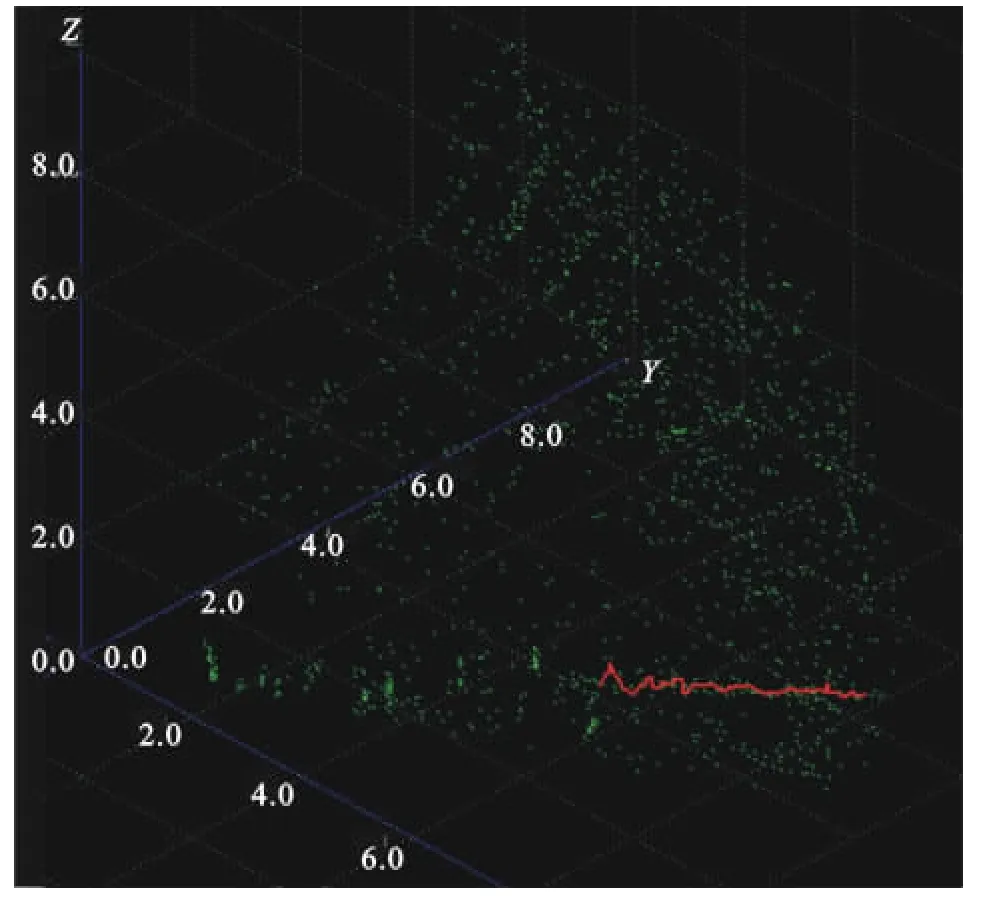
圖3 已做雜波抑制數據處理結果顯示

［1］何友.雷達數據處理及應用［M］.北京：電子工業出版社，2009.

［2］［美］斯科尼克.雷達手冊［M］.王軍譯.北京：電子工業出版社，2003.

［3］張光義.相控陣雷達技術［M］.北京：電子工業出版社，2006.

［4］吳順君.雷達信號處理和數據處理技術［M］.北京：電子工業出版社，2008.