一種基于STFT的數字信道化方法

王 開，束 坤

（船舶重工集團公司723所，揚州225001）

0 引 言

當前電子戰接收機通常要求具有大的瞬時帶寬、高頻率分辨率、大動態范圍、多信號并行處理等性能［1］。數字信道化接收機可以很好地實現上述性能。

本文闡述了一種基于短時傅立葉變換（STFT）的數字信道化方法［2］，能夠測量單脈沖信號的脈沖載波頻率fRF、脈沖到達時間tTOA、脈沖重復周期TPRI、脈沖寬度τPW、脈沖幅度AP等脈沖信號參數，并能夠分辨同時刻到達的2個信號。

1 數字濾波器組與信道化

數字信道化可以看成一個數字濾波器組［3］，即具有一個共同輸入端、多個輸出端的一組濾波器。

圖1中s （n）為輸入信號，yk（n），k＝0，1，…，K－1為輸出信號，hk（n），k＝0，1，…，K－1為第k個濾波器的沖擊響應。信號 s （n）的整個帶寬被這K個濾波器均勻分成K個子頻帶，然后分別進行濾波輸出，這K個濾波器就叫做信道化濾波器組。將1個實信號帶寬劃分成3個信道的濾波器組的情況如圖2所示。

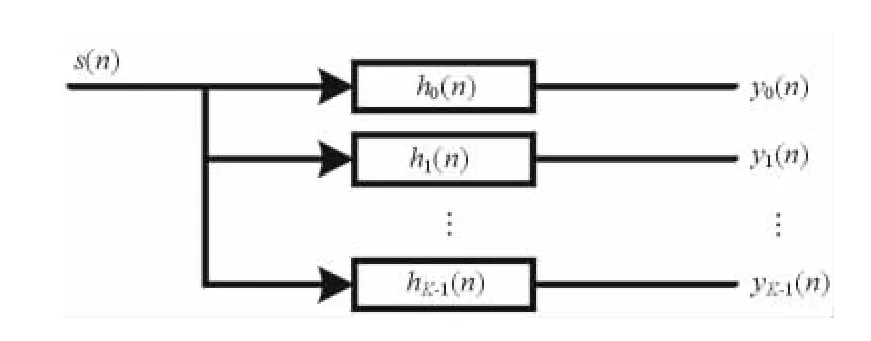
圖1 信道化濾波器組

構建上述濾波器組有很多辦法，其中最直接的方法是單獨設計這些濾波器。從理論上講，這些單獨設計的濾波器具有不同的帶寬和濾波器特性，但在實際工程中這種方法有以下幾個缺點：一是偵察接收機的頻率分辨率可能不一致，這是由于每個濾波器具有不同的帶寬和濾波特性導致的；二是濾波器組工作時運算很復雜；三是占用硬件資源多。顯然，這在實際工程中是不可行的。因此，需要設計一種各個濾波器具有相同帶寬和濾波特性、頻率分辨率一致并且運算量少的信道化接收機。

圖2 實信號三信道化濾波器組

2 基于STFT的數字信道化原理

時間序列 x （n）的N點加窗快速傅立葉變換（FFT）公式：

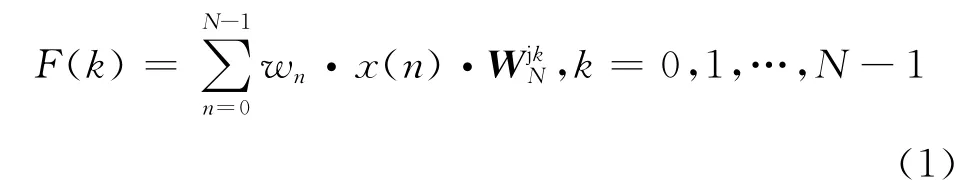
要處理一個連續的信號，就必須在不同時刻對分段的數據進行FFT運算。可以利用STFT，下式為STFT的表達式：

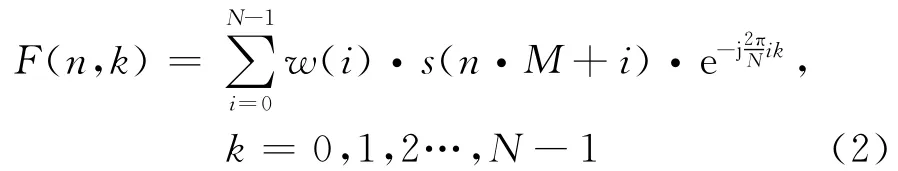
式中：n為時刻點；k為信道號；F （n ，k）為n時刻第k個信道的頻域復信號；w （n）為窗函數，其寬度為N。

窗函數的寬度決定了頻率分辨率，N越大則頻率分辨率越高；但是如果窗函數的寬度過大，就不能檢測到瞬時信號，所以這需要根據實際設計要求進行折衷。

STFT的輸出是多次、連續FFT運算的結果。此外，由于STFT引入了時間變量，因此STFT不僅能夠測量輸入信號的載頻fRF，還能夠測量輸入信號到達時間tTOA、脈沖重復周期TPRI、脈沖寬度τPW、脈沖幅度AP等參數。

基于STFT的數字信道化系統的組成和工作原理如圖3所示。

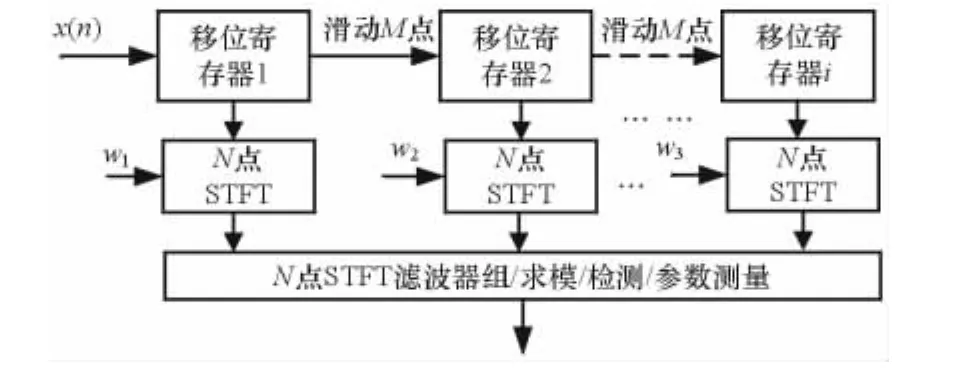
圖3 基于STFT的數字信道化系統結構

門限檢測：

脈沖到達時間：

脈沖寬度：

脈沖幅度：

VT為檢測門限電壓：

式中：Pfa為恒虛警率；Pn（i， k）為各子信道無信號時的輸出功率，即噪聲功率。

短時窗每次的滑移寬度直接影響時間分辨率。從理論上講，短時窗的滑動點數越小越好，因為這時能夠達到很高的時間分辨率，并且能夠降低檢測時信號信息的丟失。因此最理想的情況是逐點滑動，即每次短時窗只向前滑動一點，這種方式也叫做逐點滑動STFT［4］。

圖4 逐點滑動STFT示意圖

逐點滑動STFT的時間分辨率能夠達到Ts，Ts＝1／fs，fs為采樣頻率。這種情況數據重疊近乎100%。無論脈沖寬度有多短，總能夠在某一個短時窗內捕捉到，從而能夠保證信號信息無丟失。但這只是一種理想情況，如果要做逐點滑動STFT，就必須使短時窗每隔Ts滑動一次并做一次FFT，這對硬件的運算速度要求非常高，而且運算量很大，需要的硬件資源非常多。所以實際中需要在測量的時間分辨率和運算速度、運算量之間折衷考慮，一般滑動點數取N／4或者N／2。

3 仿真及結果分析

3.1 單個信號輸入

（1）輸入信號參數設置

假設輸入信號為單載頻脈沖信號，脈沖重復周期TPRI為2.56μs，占空比為50%，首脈沖的到達時間tTOA為0，脈內信號為頻率30MHz的正弦信號，幅度為1V，輸入信噪比為13dB，仿真時間長度為10個脈沖重復周期。

信號經過模數轉換采樣（采樣頻率為100MHz，信噪比為13dB）后到達STFT濾波器組，輸入信號時域波形如圖5所示。

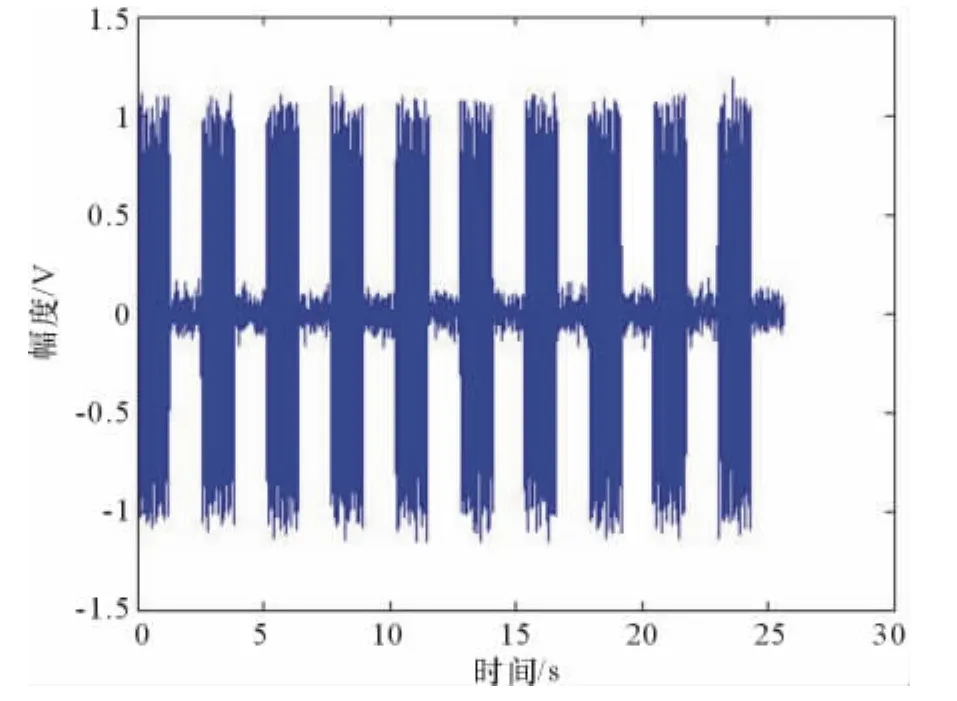
圖5 輸入信號時域波形

（2）STFT參數設置

假設STFT所用的窗函數為矩形窗，窗函數長度為128點，窗函數滑動點數M＝N／2＝64點，FFT的點數與窗函數長度相同，也為128點。經過Matlab仿真，輸入信號經過STFT濾波器組處理后輸出的信號如圖6所示。

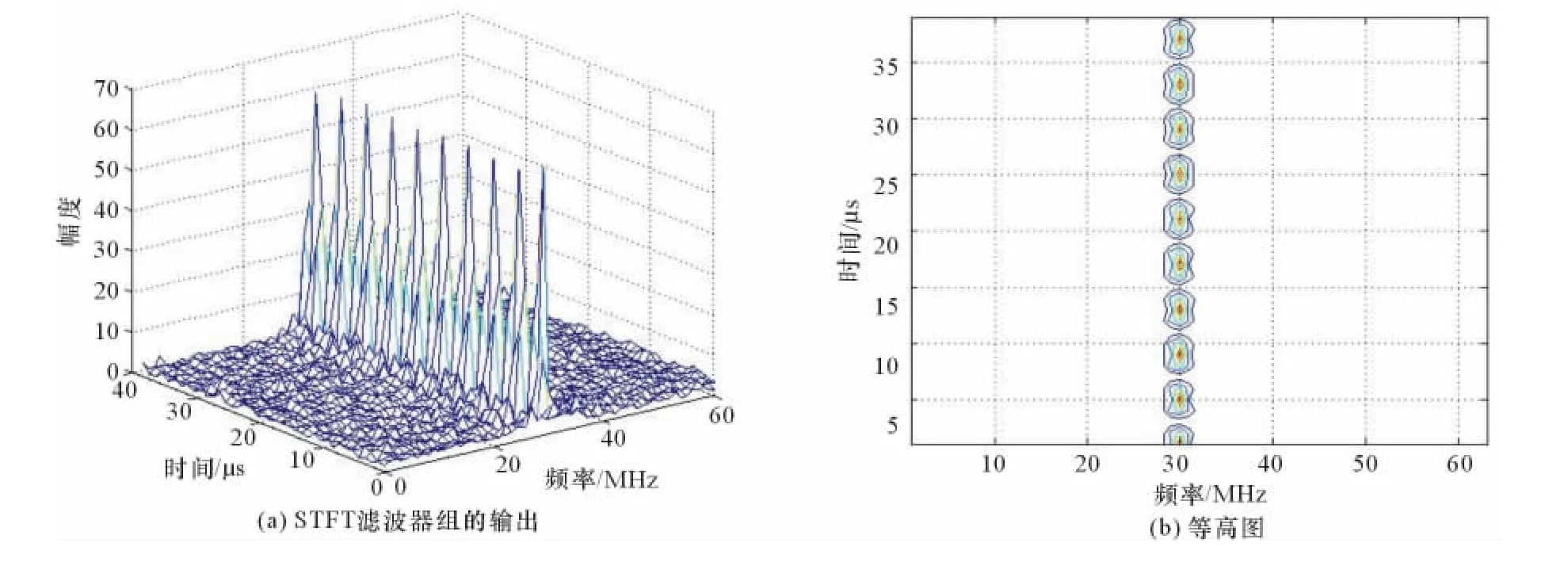
圖6 經過STFT濾波器組輸出信號的三維圖和等高圖

（3）檢測門限設置

假設發現概率為0.9，虛警率為10－6，輸入信噪比為13dB。根據公式（7）、（8）可計算出檢測門限VT≈27.6。

（4）信號時域參數測量

隨著窗函數的移動，每隔N／2點做一次FFT，得到此時刻輸出信號的功率，并與之前設置好的檢測門限比較，如果功率大于檢測門限則說明有信號存在，如果小于檢測門限判則說明沒有信號存在。經過 Matlab仿真，時域檢測結果為第1、2、4、5、6、8、9、10、…個時間窗內有信號，圖7給出了第1～16次FFT濾波器輸出的頻譜圖。

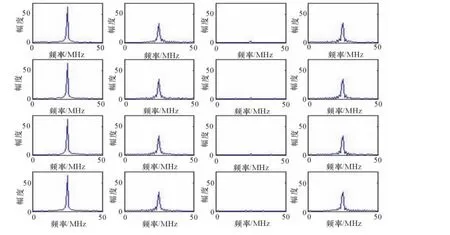
圖7 第1～16次FFT輸出的頻譜圖

從圖7中可以看出，信號在第1次FFT時已經存在，由于第1次FFT對應的時間是0時刻，由公式（4）可以得到脈沖到達時間tTOA＝0；由公式（5）可以計算出脈沖寬度τPW＝ （3－1 ）·N／2·Ts＝1.28μs，其中Ts＝1／fs為采樣周期；脈沖周期TPRI＝（8 －4 ）·N／2·Ts＝2.56μs；由公式（6）可以計算出AP＝1.2≈1。

經過檢測得出信號位于STFT濾波器組的第39信道內，由于與第1個信道相對應的頻率為0，故可得fRF＝ （39 －1 ）·fs／N ≈29.7MHz。

3.2 2個信號輸入

（1）輸入信號參數設置

假設輸入信號為時域重疊但頻域不重疊的2個單載頻脈沖信號，2個信號的脈沖重復周期、占空比和幅度都相同，分別為TPRI＝2.56μs、占空比50%、幅度1V，脈沖到達時間都為0時刻，信號1的載頻為20MHz，信號2的載頻為30MHz，仿真時間長度為10個脈沖重復周期，STFT參數設置和檢查門限設置均與前面的設置相同。輸入信號經過STFT后的輸出圖形如圖8所示。

時域檢測結果為第1、2、4、5、6、8、9、10、…個時間窗內有信號，圖9給出了第1～16次FFT濾波器輸出的頻譜圖。

圖8 經過STFT后輸出信號的三維圖和等高圖

圖9 第1～16次FFT輸出的頻譜圖

經過頻譜圖分析并計算可得出：脈沖到達時間tTOA＝0；脈沖寬度τPW＝ （3－1 ）·N／2·Ts＝1.28μs，脈沖周期TPRI＝ （8－4）·N／2·Ts＝2.56μs；AP＝1.2≈1。時域重疊的2個信號經過FFT后在頻域上能夠清楚地分辨出來。經計算得出信號1的載頻為20MHz，信號2的載頻為29.7MHz。

以上實驗說明短時傅里葉變換具有分辨多信號的能力。

4 結束語

在現代電子戰數字化接收機的設計中，信道化處理是重要的環節之一，目前也被認為是用現代技術實現寬帶數字化的主要途徑［5－6］。基于STFT的信道化方法不僅能夠測量脈沖信號的載頻fRF、脈沖到達時間tTOA、脈沖寬度τPW、脈沖幅度AP等參數，還具有多信號分辨的能力。

［1］王宏偉，趙國慶，王玉軍，等.一種寬帶數字信道化接收機［J］.西安電子科技大學學報，2010，37（3）：487－491.

［2］趙國慶.雷達對抗原理［M］.西安：西安電子科技大學出版社，1999.

［3］James Tsui.寬帶數字接收機 ［M］.楊小牛，陸安南，金飚譯.北京：電子工業出版社，2002.

［4］王宏偉.基于傅立葉變換的數字信道化及相關技術［D］.西安：西安電子科技大學，2010.

［5］楊春華，管振揮.數字信道化技術在空時聯合陣列信號處理中的應用［J］.艦船電子對抗，2009（4）：72－75.

［6］江海清，陸志宏，高梅國，等.一種數字信道化接收機參數編碼方法［J］.北京理工大學學報，2011，31（6）：713－716.