基于相位差變化率定位算法的研究

李 帥，鈕俊清，田明輝，馬 敏

（中國電子科技集團公司38所，合肥230088）

0 引 言

對于非合作輻射源的單站無源定位技術在電子對抗、偵察、監視等領域具有重要地位，受到廣泛關注［1］。傳統的單站無源定位體制是依靠單個運動觀測平臺在不同時刻測量到達角進行交叉定位［2］，其定位收斂時間長，定位精度不夠精確。

無源定位技術正朝著高精度、高速度的方向發展，主要依賴于參數測量和處理能力的提高［3－4］。現階段，相位差變化率定位算法［5－6］是依據運動學原理，提取輻射源目標和觀測平臺的相對運動信息進行定位，定位速度和精度都有了一定程度的提高，在現代戰爭中具有廣闊的應用前景。

本文結合工程使用并借助衛星工具開發包（STK）軟件對基于相位差變化率的定位算法進行了詳細的仿真實驗，研究定位算法中不同參量對定位結果的影響。

1 定位算法

1.1 基于相位差變化率的單站定位算法原理

設載機飛行速度是VA，雷達位于固定位置P，雷達與載機處于同一個平面，到達角是θ，機動單站無源定位的動力學原理如圖1所示。

當載機沿著圖1所示航線飛行時，載機與雷達之間的視線將按照角速度旋轉，即：VAsinθ＝R·，由此可得：

推導可得載機與雷達之間距離為：

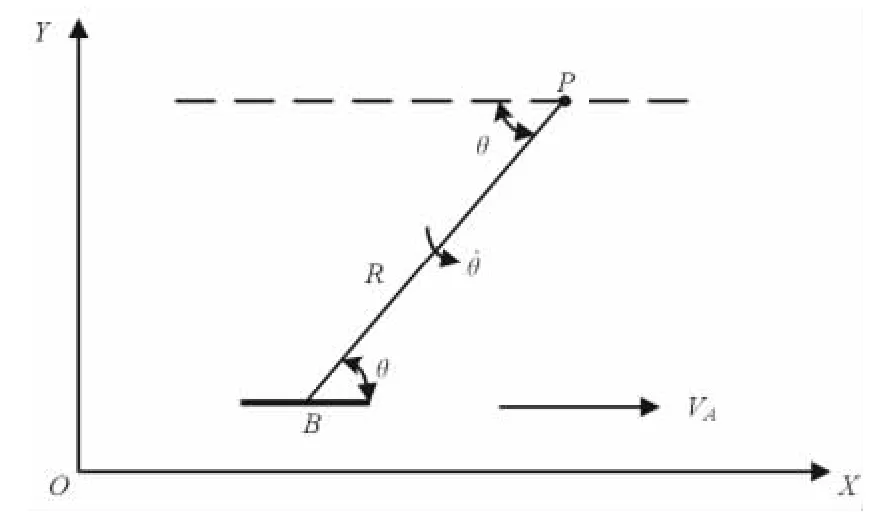
圖1 機動單站無源定位的動力學原理

式中：λ為信號波長；θ為雷達的方位角；φ·為信號相位差變化率；B為干涉儀基線長度。

再利用雷達的方位角θ，雷達的位置可以表示為：

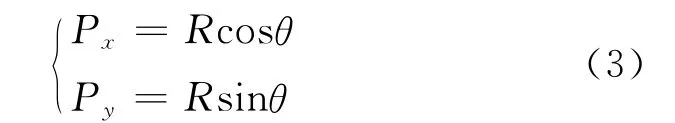
通過以上的分析可知，通過測量飛機直線運動引起的相位變化率可以獲得目標距離R，再結合雷達的到達角θ，即可確定雷達的位置（Px、Py）。

該算法的輸入參數包括測向、相位差變化率、目標頻率及對應的基線長度。現階段測向誤差和相位差變化率誤差是無法避免的，并且定位結果對其敏感。為了提高最終的目標定位速度和精度，采用以下方式進行優化解決：

（1）提高測量數據率；

（2）對高數據率的測向和相位差變化率進行卡爾曼濾波算法處理，降低隨機誤差的引入；

（3）對定位結果進行擴展卡爾曼濾波算法（EKF）［5］處理，提高定位速度和精度。

1.2 濾波算法

在實際算法應用中，由于不可避免的測量誤差，必須使用合適的濾波算法來收斂定位結果，本文選用EKF濾波算法進行定位結果濾波。

通常EKF采用的線性化方法是將非線性狀態方程按泰勒級數展開。

探測目標微分方程為連續狀態方程，記為：

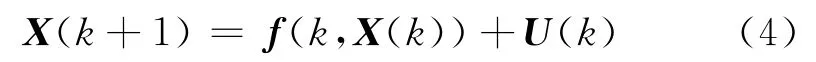
量測方程：

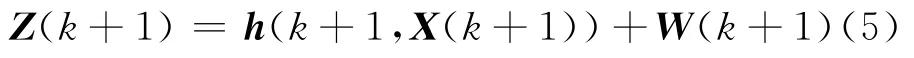
式中：U（k）為過程噪聲；W（k＋1）為量測噪聲；兩者均為高斯零均值噪聲。

泰勒級數的展開式只保留一階項，即可得到一階擴展卡爾曼濾波的狀態方程：

式中：fX（k）為雅各比矩陣。

狀態的一步預測：

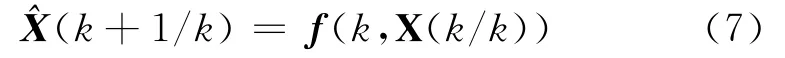
協方差的一步預測：

式中：Q（k）為過程噪聲協方差。

量測預測值：

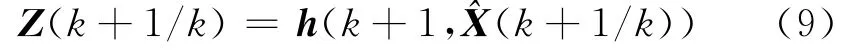
相伴的協方差：

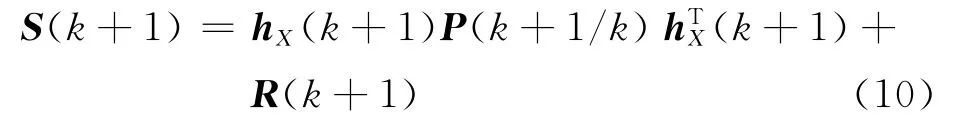
式中：hX（k＋1）為雅各比矩陣；R（k＋1）為量測噪聲協方差。

增益矩陣：

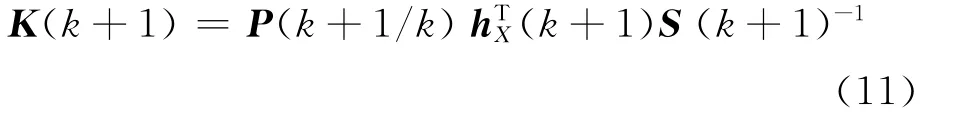
狀態更新方程：

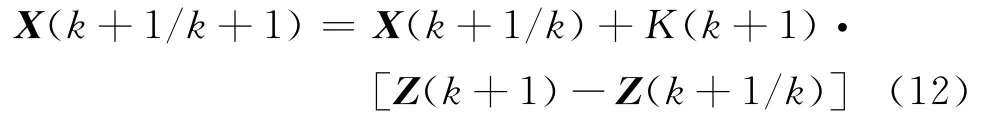
協方差更新方程：

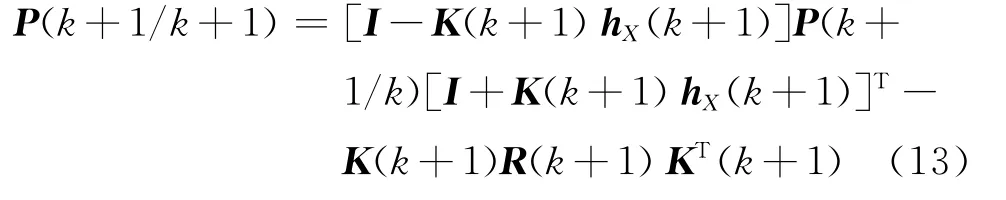
式中：I為與協方差同維的單位矩陣。

EKF在應用于非線性不強的問題上具有不錯的性能，同時其計算復雜度不高，總體上看其費效比較高。

1.3 定位算法流程

基于相位差變化率的輻射源定位流程如圖2所示。對于數據處理分系統的輸入（測向信息、相位差信息），在其進行定位結算之前進行二維卡爾曼濾波，減少隨機誤差對測量值的影響，提高定位結算的精度；結合測向濾波值、相位差變化率濾波值進行定位結算，并對定位結算結果再次進行EKF濾波，進一步提高定位解算精度；最后，通過坐標變換，可得定位目標的經緯度。

2 仿真實驗

仿真實驗借助STK軟件，進行了仿真實驗參數的設置，包括機載平臺的速度、高度、目標截距等，同時在仿真時也引入了工程中需要考慮的測向測量誤差、航向角誤差等。仿真實驗包括以下4個方面：

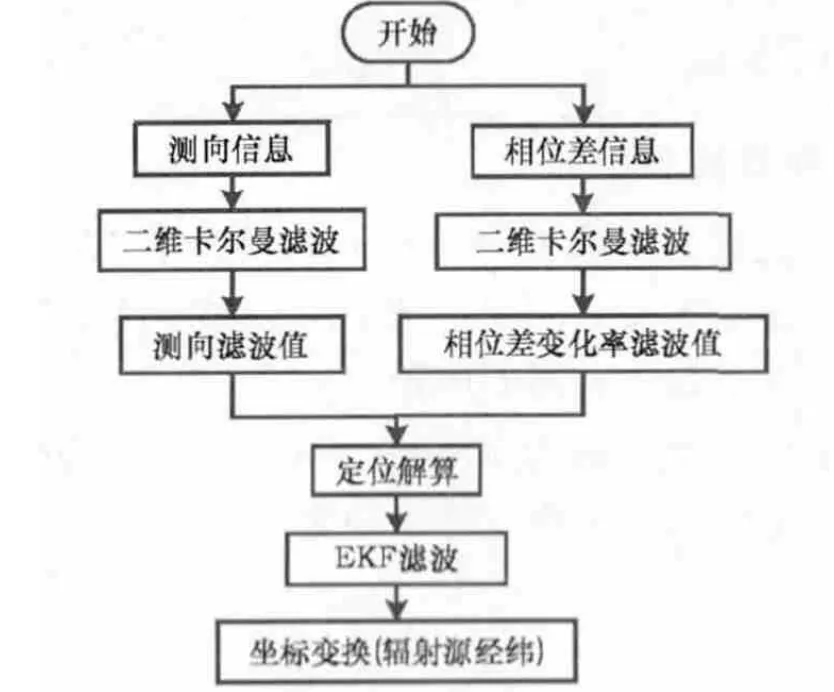
圖2 基于相位差變化率定位算法流程

（1）相同的仿真實驗參數和仿真場景，研究測向精度對定位結果的影響；

（2）相同的仿真實驗參數和仿真場景，研究相位差變化率對定位結果的影響；

（3）相同的仿真實驗參數和仿真場景，研究目標頻率對定位結果的影響；

（4）相同的仿真實驗參數和仿真場景，研究截距對定位結果的影響。

針對上面所述的4個方面，對應以下的4個仿真實驗，通過計算給出定位結果，并分析總結不同參數對本文算法定位結果的影響。

2.1 仿真實驗1

在其他仿真實驗參數相同的情況下，研究目標探測方位角精度不同對本文算法定位結果的影響。方位精度分別為1.0°、1.6°、2.2°、2.8°，測向精度對定位結果的影響如圖3所示，不同測向精度對應的定位結果如表1所示。

圖3 測向精度對定位結果的影響

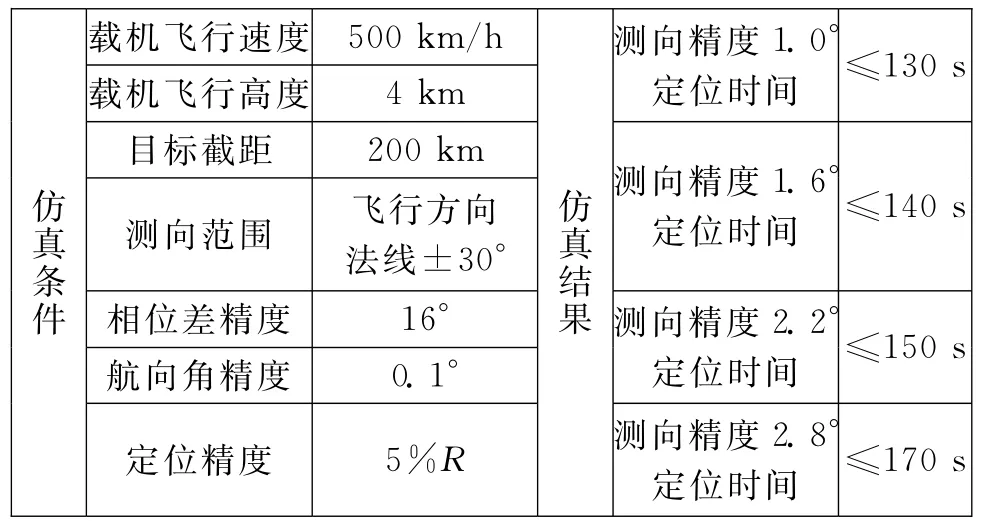
表1 不同測向精度對應的定位結果

2.2 仿真實驗2

在其他仿真實驗參數相同的情況下，研究不同目標探測相位差精度對本文算法定位結果的影響。相位差精度分別為10°、14°、18°、22°，相位差精度對定位結果的影響如圖4所示，不同相位差精度對應的定位結果如表2所示。

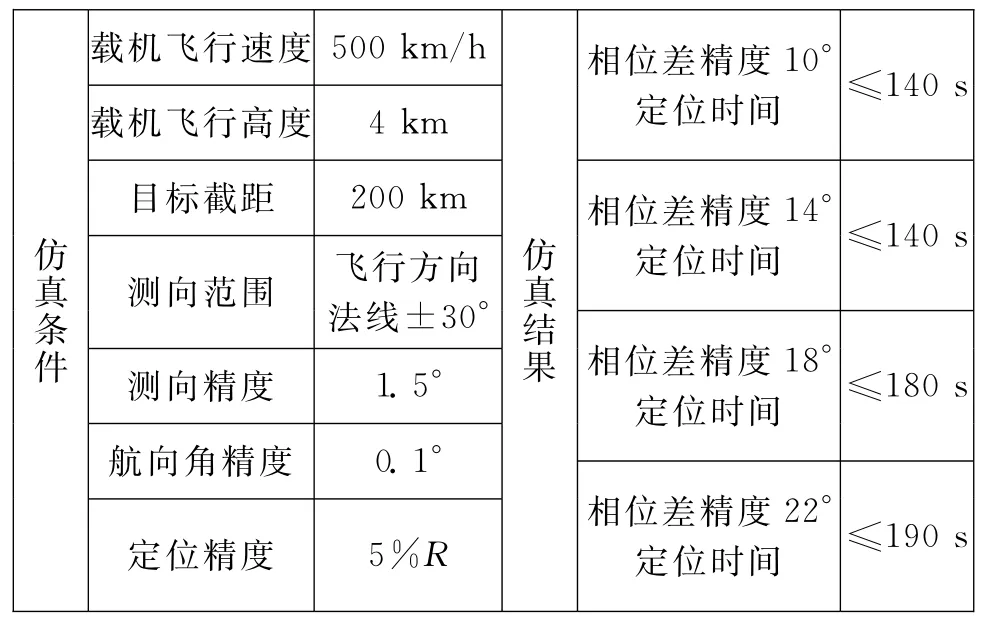
表2 不同相位差精度對應的定位結果

2.3 仿真實驗3

在其他仿真實驗參數相同的情況下，研究不同探測目標頻率對本文算法定位結果的影響。目標頻率對定位結果的影響如圖5所示。目標頻率及基線長度參數對照如表3所示。

圖4 相位差精度對定位結果的影響

表3 目標頻率及基線長度參數

2.4 仿真實驗4

在其他仿真實驗參數相同的情況下，研究不同目標截距對本文算法定位結果的影響。目標截距對定位結果的影響如圖6所示。

目標截距分別為100km、150km、200km。不同目標截距對應的定位結果如表4所示。

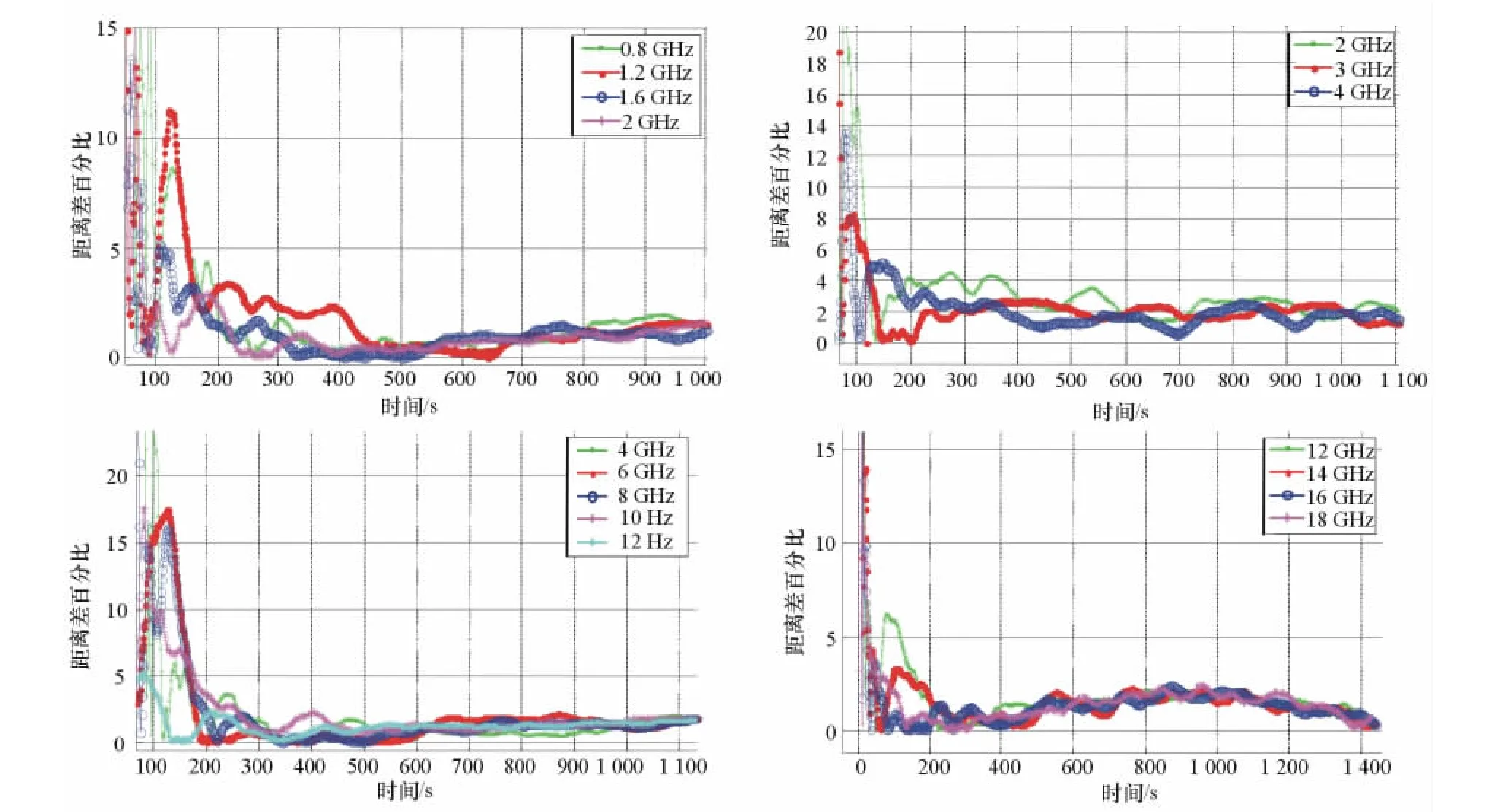
圖5 目標頻率對定位結果的影響

圖6 目標截距對定位結果的影響

從仿真實驗結果可知：隨著測向精度的增加，定位時長也在逐漸增加；隨著相位差精度的增加，定位時長也在逐漸增加；隨著目標頻率的增加，定位時長相對比較穩定，但仍有減少的趨勢；隨著目標截距的增加，定位時長相對穩定。

表4 不同目標截距對應的定位結果

3 結束語

綜上所述，基于相位差變化率定位算法引入了卡爾曼濾波和擴展卡爾曼濾波，通過仿真實驗，驗證了該算法的可行性和魯棒性。在同等的定位精度要求下，隨著測向精度和相位差精度的逐漸增加，定位時長逐漸增加，但仍在工程應用可以接受范圍之內。

隨著目標頻率的增加，定位時長在保持穩定的基礎上有減少的趨勢，而目標截距對定位時長影響不大。總的來說，基于相位差變化率定位算法具有很強的實用性，可以滿足實際工程應用快速精確定位的需要。

［1］孫仲康.基于運動學原理的無源定位技術［J］.制導與引信，2001，22（1）：40－44.

［2］姚坤，陳天麒，李立萍.單站無源定位跟蹤方法研究［D］.成都：電子科技大學，2003.

［3］許耀偉，孫仲康.利用相位差變化率對固定輻射源的無源被動定位.系統工程與電子技術，1999，21（3）：34－37.

［4］Xi W，Yu B Z，Wang S S.Theoretical analysis of direct finding targets with rolling－airframe passive radar by phase interference technique［A］.Proceedings of International Conference on Radar［C］，2006：1－4.

［5］程詠梅，潘泉，張洪才，等.基于擴展卡爾曼濾波的多站被動式融合跟蹤［J］.系統仿真學報，2003，15（4）：548－550.

［6］張國毅，宋德亮，陳楓.PRI變化雷達信號相位差變化率定位法研究［J］.艦船電子對抗，2010，33（3）：35－38.