基于數字正交變換的雙模DRFM技術研究

呂東澤，喻旭偉，王 俐，蔡易君

（中國電子科技集團公司29所，成都610036）

0 引 言

數字射頻存儲器（DRFM）可以產生與雷達信號相干的干擾信號，對采用多普勒、脈沖壓縮等技術的相干雷達具有很好的干擾效果，因此DRFM在電子對抗領域得到了廣泛的關注和應用［1］。DRFM根據其量化方式分為幅度量化和相位量化2種。其中幅度量化DRFM具有輸出信噪比高、無模糊帶寬較大等優點，但是其在對干擾信號進行相位調制時較為復雜；相位量化DRFM具有動態范圍大、實現結構簡單等優點，但是當存在多信號時，會出現小信號抑制現象［2］。

為了使DRFM可根據實際情況靈活選取量化方式，本文提出了幅度和相位雙模量化的DRFM系統。但是傳統DRFM采用的模擬正交變換方法的鏡像抑制比最高只能達到30dB［3－4］。為了簡化結構、提升性能，本文在雙模DRFM中采用數字正交變換方法形成兩正交支路。該DRFM系統具有結構簡單、應用靈活、鏡像抑制比高等優點。

1 正交雙模DRFM結構

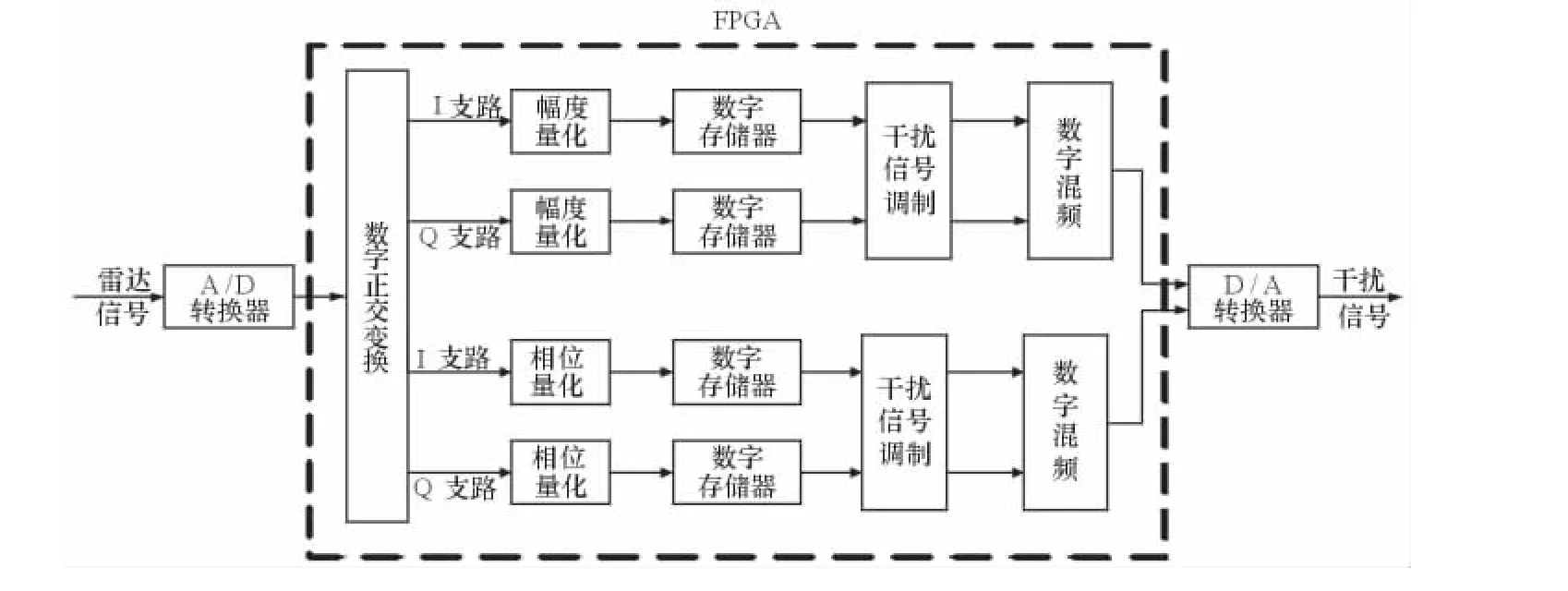
圖1 數字正交雙模DRFM系統結構

基于數字正交變換方法的雙模DRFM系統的結構如圖1所示。該DRFM只需要采用1個模擬／數字（A／D）轉換器、1個現場可編程門陣列（FPGA）和1個數字／模擬（D／A）轉換器，利用FPGA實現數字正交變換、量化、雷達信號存儲、干擾信號調制、混頻等功能。該DRFM系統相比傳統DRFM系統具有結構簡單、功能豐富、易于實現等優點。

2 數字正交變換法

DRFM接收到的雷達帶通信號表示為：

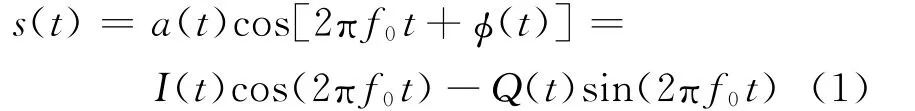
式 中： I（t）＝ a（t）cos［φ（t）］；Q（t）＝a（t）sin［φ（t）］。

利用采樣頻率fs＝4f0／（2m－1）且fs≥2B對s（t）進行采樣，其中m表示正整數，B表示信號帶寬，可得采樣序列為：

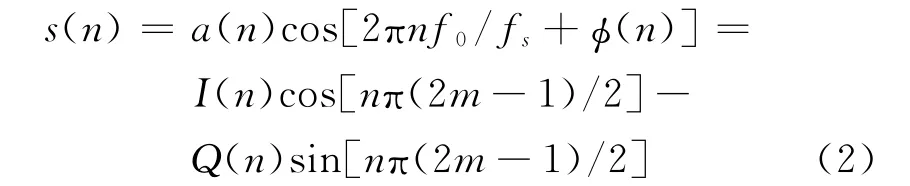
式 中： I（t）＝ a（t）cos［φ（n）］；Q（t）＝a（t）sin［φ（n）］。

常用的數字正交變換方法有Hilbert變換法、低通濾波法和多相濾波法，本文分別對其進行分析。

2.1 基于Hilbert濾波法的DRFM

Hilbert變換的理想頻譜為［5］：

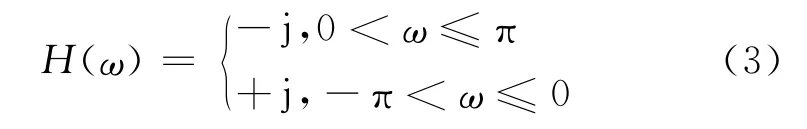
由上式可知，Hilbert變換為90°移相器，通過該變換后信號只有相位變換，幅度沒有變化。DRFM接收到的雷達實信號經過Hilbert變換后變為解析信號，變換后頻譜為：

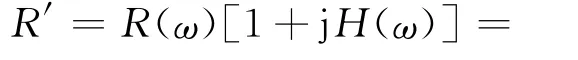
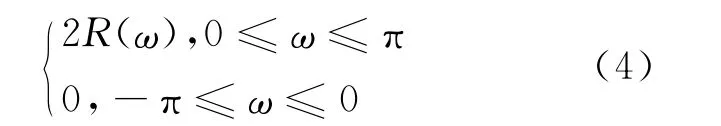
一般利用數字濾波器來實現Hilbert濾波器，理想Hilbert濾波器沖擊響應為：

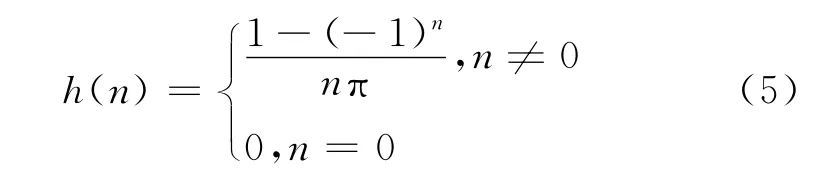
經過Hilbert濾波器后，信號會產生（M－1）／2個采樣點的延遲，M為濾波器階數。由于采用偶數階Hilbert濾波器會使得延遲為非整數采樣點，從而增加延遲匹配的難度，因此一般Hilbert濾波器都采用奇數階數。

綜上，基于Hilbert濾波法的數字正交變換示意圖如圖2所示。將A／D轉換后的雷達信號通過Hilbert濾波器使其與原信號正交，再將另一支路進行延時處理使2個支路時間匹配，然后對其量化。

圖2 Hilbert濾波法示意圖

2.2 基于低通濾波法的DRFM

基于低通濾波法的數字正交變換如圖3所示，將經過A／D轉換器的雷達信號分為2路，分別利用數控振蕩器（NCO）產生的正交信號相乘，然后經過低通濾波器濾除高頻分量，再對2個支路分別量化。

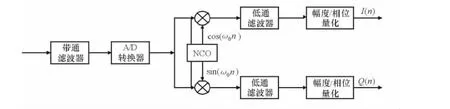
圖3 低通濾波法示意圖

NCO分別產生cos（ω0n）和sin（ω0n），與s（n）相乘（ω0＝2πf0／fs）可得［6］：

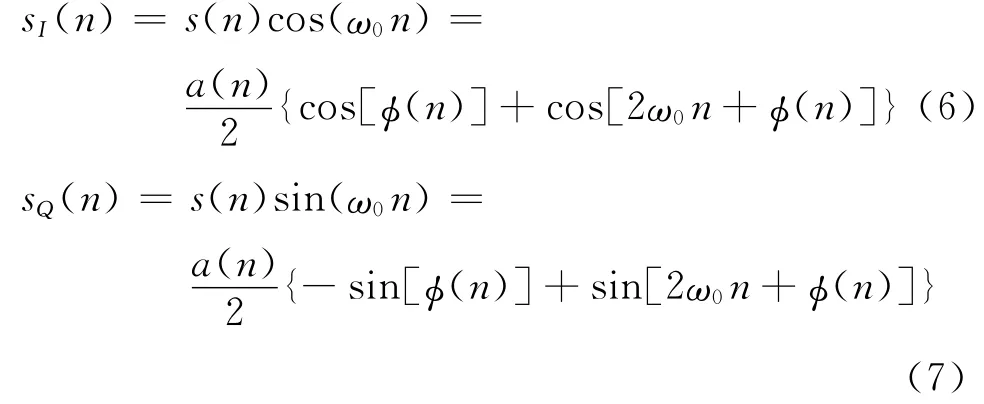
對式（6）、（7）再進行低通濾波后，可得：

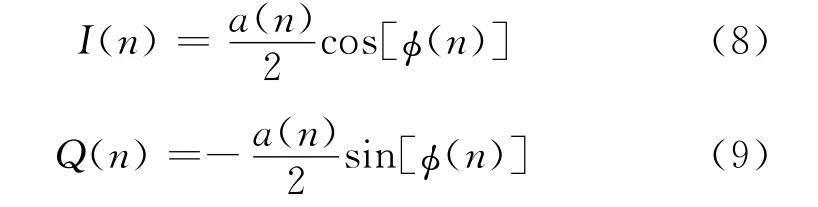
低通濾波法中由于I、Q 2個支路采用相同的低通濾波器參數，因此2個支路具有較好的一致性。

2.3 基于多相濾波法的DRFM

由式（2）中采樣后的序列可得：

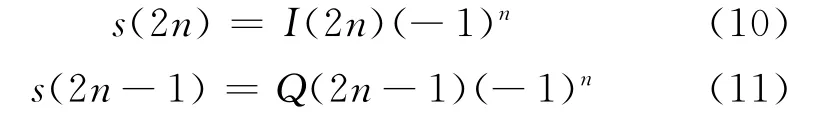
對s（n）進行奇、偶抽取和符號變換可得：

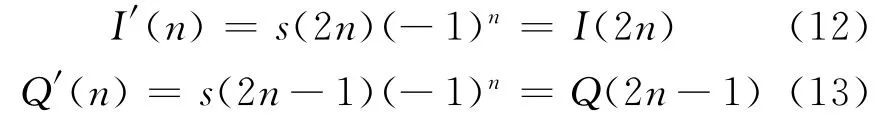
式中：I′（n）和Q′（n）分別為I（n）和Q（n）的2倍抽取，由抽取原理可知，只要I′（n）和Q′（n）數字譜小于π／2即fs≥4B，則其2倍抽取可以無失真地表示原序列［7］。它們的頻譜相差1個相位因子ejω／2，相當于時域相差1／2個采樣時間，可以采用2個延時濾波器對其偏差進行校正，延時校正濾波器可以采用內插因子為4的多項濾波內插器的分支濾波器［8－9］：HI1（ejω）＝1，HQ1（ejω）＝ejω／2或者 HI2（ejw）＝ejω／4，HQ2（ejω）＝ejω3／4。

因此基于多相濾波法DRFM的正交變換結構如圖4所示，首先對經過A／D轉換器的雷達信號進行奇、偶抽取和符號變換獲得I、Q 2個支路，然后利用多項濾波器的分支濾波器實現不同的分數相移從而使I、Q 2路信號時序匹配。

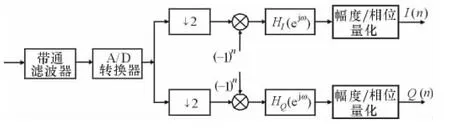
圖4 多相濾波法示意圖

3 仿真分析

利用Matlab對基于數字正交變換的雙模DRFM進行仿真分析：接收到的雷達信號頻率為f0＝120MHz，幅度量化位數為8bit，相位量化位數為3bit，Hilbert濾波器、低通濾波器的階數均為33，多相濾波器的分支濾波器為8階。

處理前信號頻譜及經過3種雙模DRFM的信號頻譜如圖5所示，圖（a）表示處理前原始信號頻譜；（b）、（c）、（d）分別表示利用3種方法經過濾波器后，再進行8bit幅度量化、3bit相位量化后信號頻譜。從圖5可見，處理前的信號頻譜存在干擾峰值，雙模DRFM可以有效對信號進行幅度和相位量化，3種正交變換方法均可有效抑制干擾。

采用3種方法的DRFM隨不同頻移其鏡像抑制比（IR）的變化如圖6所示。由圖6可見，低通濾波法隨著頻移的變化其IR一直保持較好的性能；多相濾波法在頻移較小的范圍內可以保持較好的IR性能，但隨著頻移變大，IR性能隨之大幅度下降；Hilbert法最大IR低于其他2種方法，但是相比多相濾波法可以在更廣的頻移范圍內保持IR性能，超過范圍后隨著頻移的增大IR性能下降速度低于多相濾波法。

4 結束語

本文首先提出了雙模體制的DRFM系統，該DRFM結構僅需1個A／D轉換器、1個FPGA和1個D／A轉換器，可以有效對雷達信號進行幅度、相位量化，其結構簡單且功能豐富。雙模DRFM中采用數字正交變換方法相比模擬方法可以大幅度提升DRFM的鏡像抑制比，其中Hilbert法可達到的最優IR在3種方法中最低，超出一定頻移范圍后多相濾波法隨頻移變化性能下降最快，低通濾波法鏡像抑制性能隨頻移變化較小。

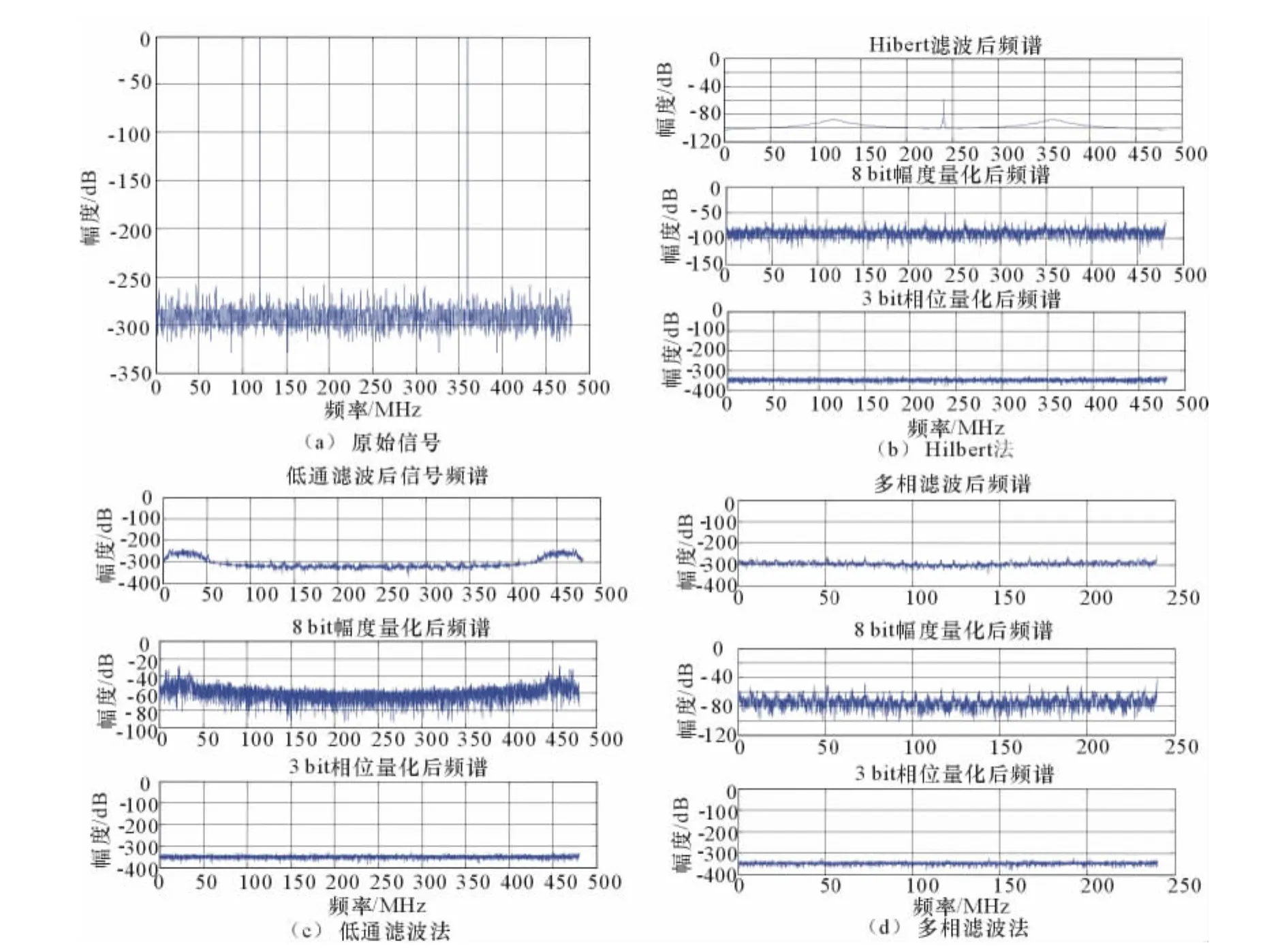
圖5 雷達信號及3種方法雙模DRFM處理后頻譜

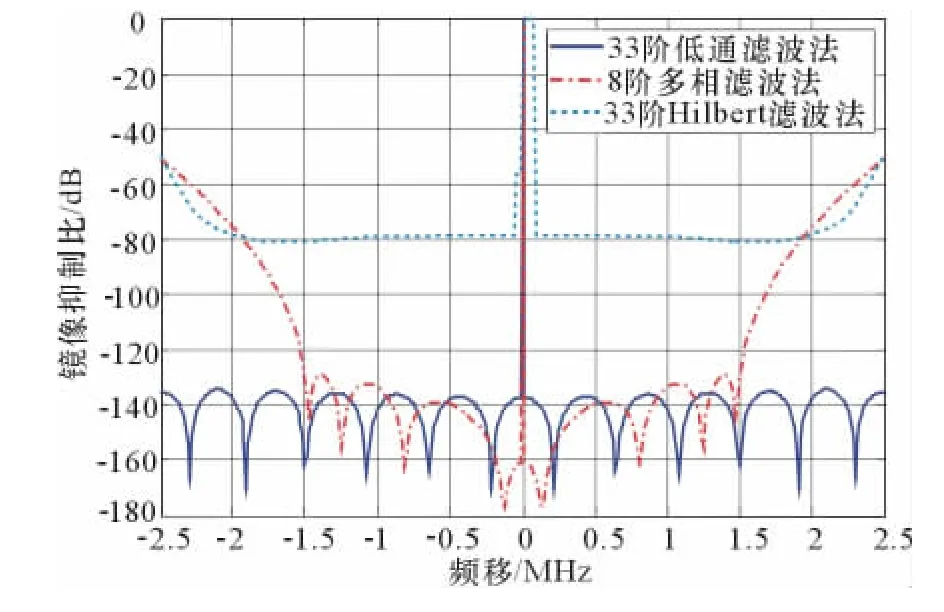
圖6 鏡像抑制比隨頻移變化

［1］Schleher D C.Electronic Warefare in The Information Age［M］.Boston：Artech House，2000.

［2］李菊.基于幅相量化的DRFM 技術［J］.上海航天，2008（5）：57－60.

［3］邱兆坤.基于Hilbert變換的正交檢波器設計新方法［J］.系統工程與電子技術，2010，10（32）：2045－2048.

［4］曾濤，龍騰，毛二可.一種新的中頻采樣濾波器的設計與實現［J］.電子學報，2000，28（6）：51－54.

［5］謝小娟，楊凌云.數字正交分解算法的研究［J］.山西電子技術，2007（6）：83－87.

［6］徐新.數字接收機中I／Q解調算法的研究［D］.成都：電子科技大學，2005.

［7］藍金巧，孫曉聞，吳順君.基于多相濾波器的數字正交檢波濾波器的選擇［J］.計算機工程與應用，2004（18）：215－224.

［8］楊小牛，樓才義，徐建良.軟件無線電原理與應用［M］.北京：電子工業出版社，2001.

［9］Pellon L E.A double Nyquist digital product dector for quadrature sampling［J］.IEEE Transactions on Signal Processing，1992，40（7）：1670－1681.