模糊自適應PID控制在主動磁懸浮系統中的研究

鄭仲橋，張燕紅

（1. 常州工學院 電子信息與電氣工程學院，常州 213002；2. 上海大學 機電工程與自動化學院，上海 200072）

0 引言

由于主動磁懸浮軸承能夠實現非接觸支承，具有無機械磨損、無需潤滑、工作溫度范圍大、工作極限轉速高等優點，在國內外得到了迅速的發展，已經在軍工、航天等國防工業部門中逐步應用，并向民用工業，如航空、機床、化工、能源等工業領域推廣[1,2]。但是在主動磁懸浮控制系統中，由于電磁鐵磁性材料的非線性及外界干擾信號的影響，使得主動磁懸浮控制系統是一個典型的非線性、參數不確定的控制系統，以往使用的常規PID控制算法很難使系統獲得較好的響應特性，而且參數的調整也比較困難，很難滿足控制系統的高穩定性和強抗擾性的要求。而在整個主動磁懸浮控制統中，磁懸浮軸承的動態特性及轉子的穩態精度和設計的控制器的好壞有直接的關系，因此，主動磁懸浮系統中的控制器的設計成了一個研究的熱點問題。本文根據磁懸浮系統的非線性、參數不確定的特點，結合模糊控制和PID控制的特點，設計了模糊自適應PID控制器，來改善主動磁懸浮控制系統的控制精度和穩態特性。

1 主動磁懸浮控制系統模型

單自由度主動磁懸浮支承系統的原理圖如圖1所示，其結構采用差動的連接方式，單自由度主動磁懸浮控制系統由位移傳感器、轉子（懸浮體）、控制器、功率放大器和電磁鐵五部分組成。轉子的平衡位置為x0，當轉子的實際位置發生偏移量x時，位移傳感器檢測到這一偏移信號并轉換成相應的電信號Ux，Ux與轉子平衡時的期望電壓Ur進行比較，得到偏差信號Ue，進入控制器進行相應的運算，得到控制信號Uc，經過功率放大器輸出控制電流信號，從而調節了電磁線圈中的電流的大小，改變了電磁鐵產生的電磁力的大小，最終使得轉子的位置減小偏移直至穩定懸浮。

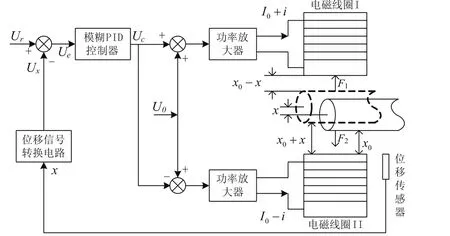
圖1 單自由度磁懸浮支承系統的結構圖

在圖1中，Ur為轉子處于平衡位置時對應的輸入電壓值，Ux為轉子實際位置所對應的電壓值，Ue=Ur-Ux為偏差信號，Uc為模糊自適應PID控制器的輸出信號，U0為上下兩個電磁線圈的偏磁電流所需的電壓值，I0為偏磁電流分量。

當質量為m的轉軸在兩個磁鐵之間處于平衡時，假設忽略繞組漏磁、鐵芯和轉子中的磁阻及磁性材料的磁滯和渦流，那么上下兩電磁鐵產生的電磁力在轉軸上的合力為零。當轉軸偏離平衡位置時，偏離位移量為x，為了使轉軸能回到原來的平衡位置，必須加一個控制電流i，使電磁鐵I的磁力增加，電磁鐵II的磁力減小。兩個電磁鐵產生的電磁力分別為：

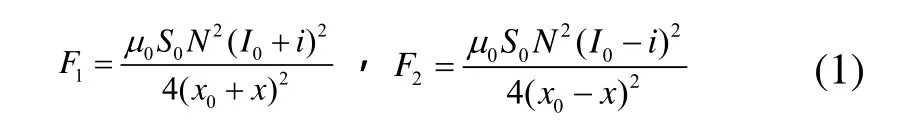
式(1)中：μ0為氣隙磁導率，μ0=4π×10-7H/m，S0為磁極氣隙的截面積(m2)，N為電磁鐵線圈的匝數，I0為電磁線圈的偏置電流(A)，x0是轉子平衡時電磁鐵與轉子軸中心線之間的距離；x為轉子偏離中心位置在該自由度上的位移(m)，i為控制電流分量。F1和F2分別為兩個電磁鐵產生的電磁力。

作用在轉子上的合力為：

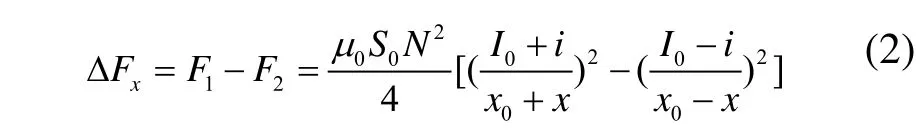
所以可以得到：

在轉子平衡位置(即x=0， 0I= )，將式(1)展開成泰勒級數，并略去高階小量，得：

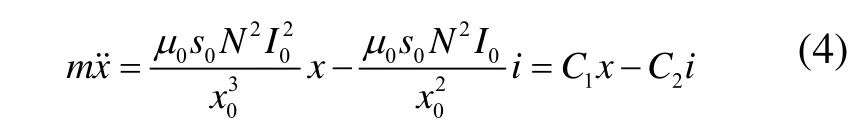
對式(4)進行拉式變換，可以得到：

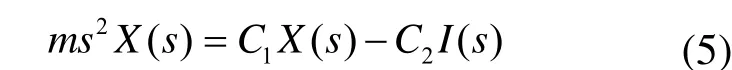
得到主動磁懸浮系統開環傳遞函數：

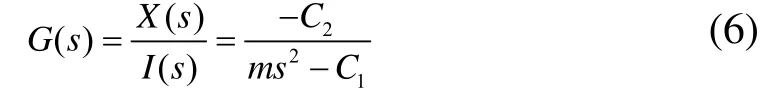
從式(6)可以看出，系統有兩個極點，其中一個極點位于S平面的右半平面，造成開環控制系統不穩定。

2 模糊自適應PID控制器

2.1 模糊自適應PID控制器的組成

主動磁懸浮系統模糊控制器的設計如圖2所示。

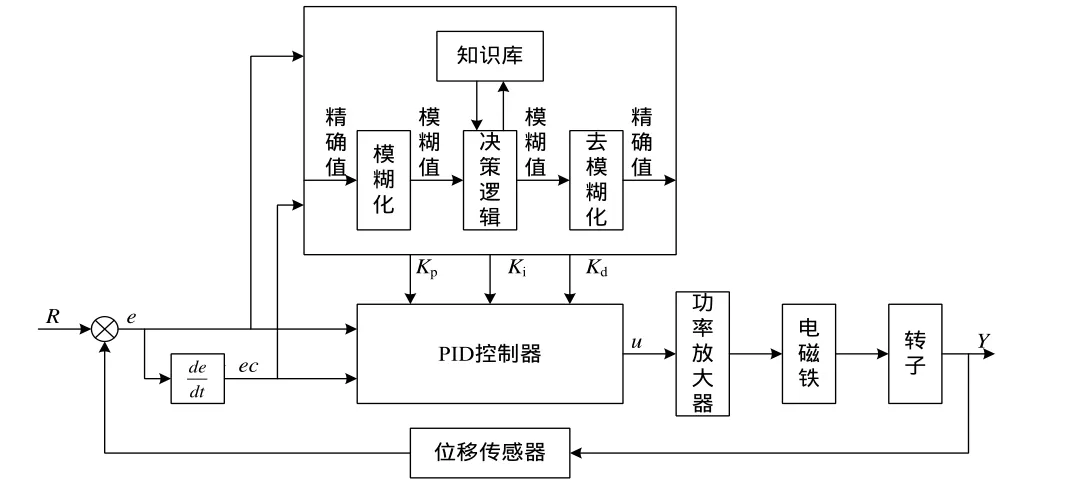
圖2 主動磁懸浮模糊PID控制器

在圖2中，R為給定轉子平衡位置，Y為轉子的實際位置，e為轉子的位移偏差信號，de/dt為轉子位置偏差的變化率，u為模糊自適應PID控制器的輸出信號，即加在電磁鐵線圈上的電壓信號。當主動磁懸浮系統受到擾動影響時，使得轉子偏離平衡位置，下降x時，即轉子與電磁鐵上線圈的距離偏大，位移傳感器檢測到轉子此時的實際位置并轉化為相應的電壓信號，與轉子平衡位置所對應的電壓信號相比較，得到偏差信號e和偏差的變化率信號ec，這兩個信號進入模糊控制器中，經過模糊化、模糊規則推理、模糊決策和解模糊化，在線整定PID控制器的三個參數Kp，Ki和Kd，使其達到最優化，經過PID控制器計算，得到控制信號增大，從而使得上線圈中的電流增大，下線圈中的電流減少，使得上線圈的電磁力F1增加，從而調節轉子慢慢向上移動，直至轉子回到平衡位置，實現轉子的穩定懸浮。

普通的增量式PID控制算法為：

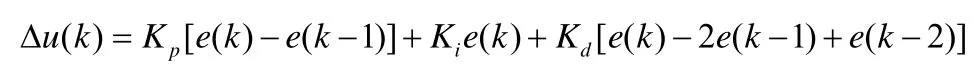
其中e(k)=r(k)-y(k)，Kp、Ki和Kd為PID控制器的比例、積分和微分系數，模糊控制就是通過模糊推理在線整定Kp、Ki和Kd，送入PID控制器中進行計算得到控制信號u，從而調整線圈中的電流信號來實現轉子的位置的調節。

2.2 模糊化和隸屬度函數

從圖2可以看出，模糊推理機構的輸入信號為誤差信號e和誤差變化率ec，PID控制器的三個系數Kp、Ki和Kd為輸出信號[3]。在轉子偏離平衡位置較大時，實行大的控制量，粗調控制量，來增度系數；被稱為主動磁懸浮系統的電流剛加系統調整的快速性；在轉子偏離平衡位置較近時，實行細調控制量，來獲得較好的穩態精度。因此選取輸入輸出變量e、ec的論域為{-3,-1.5,-0.5, 0, 0.5,1.5,3}，Kp的論域為{-0.3,-0.2,-0.1, 0,0.1,0.2,0.3}，Ki的論域為{-0.06,-0.04,-0.02, 0,0.02,0.04,0.06}，Kd的論域為{-3,-2,-1, 0,1,2,3}，對應的語言變量值分別定義為NB (負大)、NM (負中)、NS(負小)、ZO(零)、PS(正小)、PM (正中)、PB(正大)。e、ec、Kp、Ki和Kd的隸屬度函數均采用三角波函數[4]，如圖3～圖6所示。

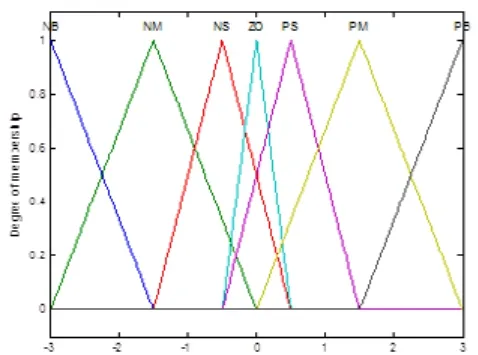
圖3 輸入量e和ec的隸屬度函數

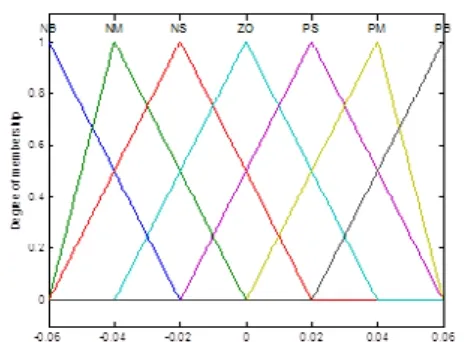
圖5 Ki的隸屬度函數

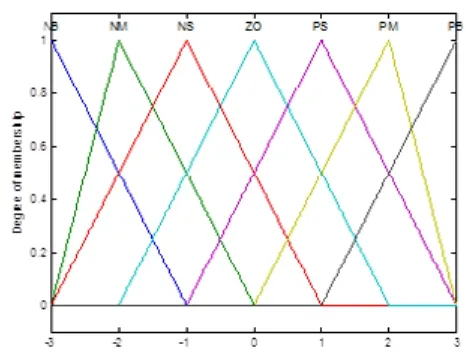
圖6 Kd的隸屬度函數

2.3 模糊推理

在主動磁懸浮模糊自適應PID控制器中，模糊控制器輸出的三個參數Kp、Ki和Kd對系統的輸出影響較大，比例系數Kp能減小轉子與平衡位置的距離，加快轉子回復到平衡位置的速度，Kp越大，主動磁懸浮的轉子回復到平衡位置的速度越快，但是過大的Kp會使得磁懸浮系統變得不穩定；積分系數Ki可以消除轉子實際位置與平衡位置之間的距離，Ki越大，轉子和平衡位置之間的誤差消除的就越快，但如果Ki過大,會產生積分飽和現象，使控制系統產生大的超調；Ki過小，使轉子很難精確地回復到平衡位置，影響系統的控制精度。微分系數Kd可以改善系統的動態特性，但是Kd過大，會延長轉子回復到平衡位置的時間，而且會降低系統的抗干擾性能。根據以上分析，同時考慮三個參數之間的相互影響，建立模糊推理語言規則。表1～表3分別為Kp、Ki和Kd的模糊控制規則。

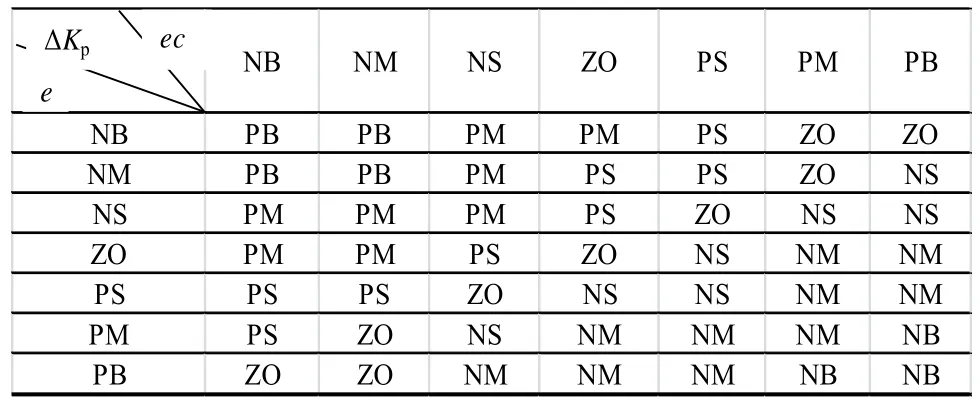
表1 Kd的模糊規則表

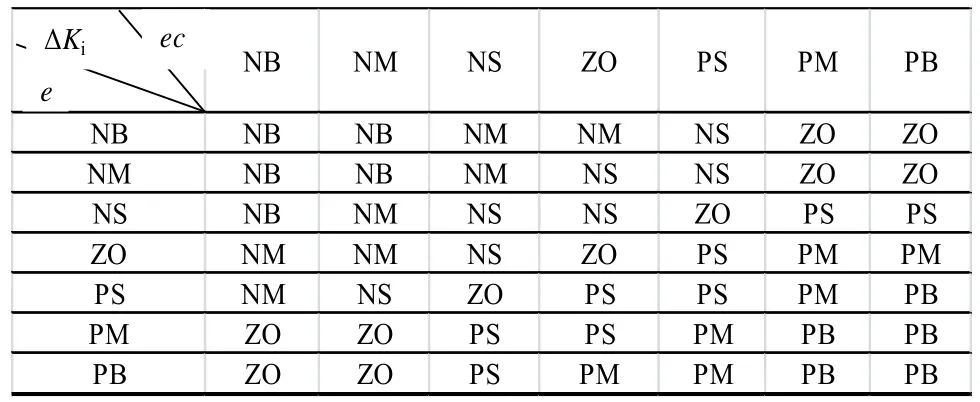
表2 Ki的模糊規則表

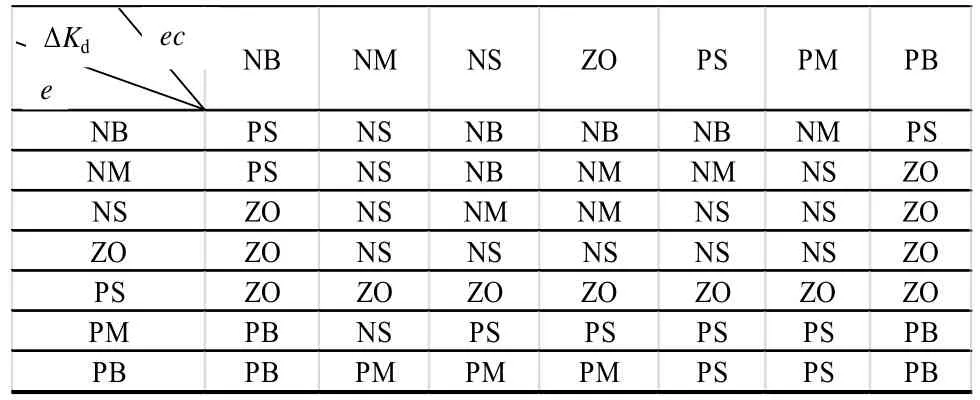
表3 Kd的模糊規則表

模糊控制器的輸入輸出之間的關系如圖7所示。

2.4 解模糊化

采用工業控制中廣泛使用的去模糊化方法-加權平均法[5]，求得最終的△Kp、△Ki和△Kd，通過下面計算公式計算出Kp、Ki和Kd。

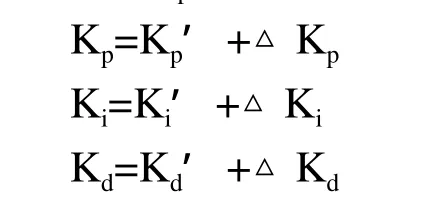
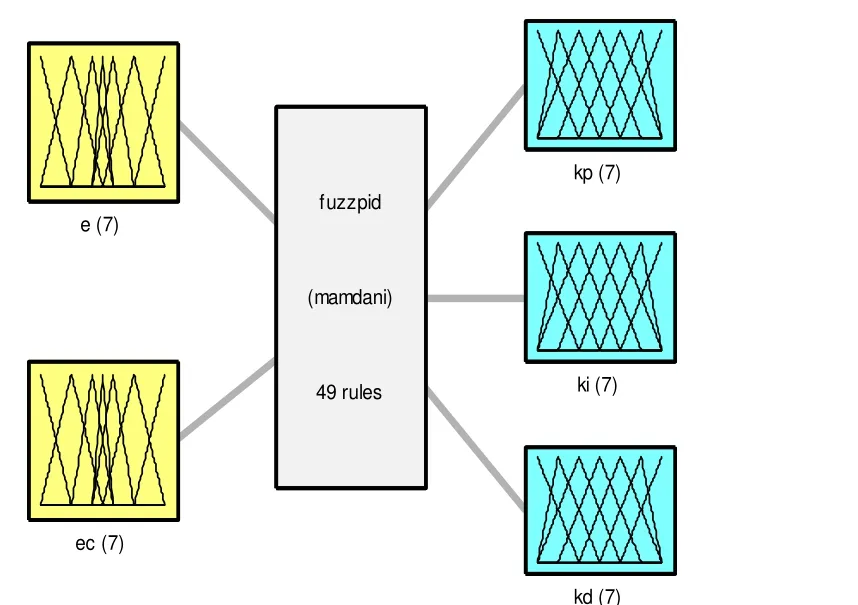
圖7 模糊控制器的輸入輸出之間的關系

3 主動磁懸浮系統仿真及分析

在主動磁懸浮控制系統中，涉及的參數為：m= 12kg，x0=0.5×10-3m，I0= 3.0A，μ0= 4π×10-7Vs/Am，s0= 340mm2，N = 190，把這些參數代入到方程(6)，可以得到主動磁懸浮控制系統開環傳遞函數為：

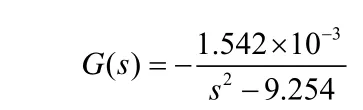
在MATLAB下進行編程仿真[6,7]，當系統不存在擾動信號時，系統的輸入信號為單位階躍信號，系統的輸出如圖8所示，Kp、Ki和Kd的整定曲線如圖9～圖11所示。

模糊控制自適應PID控制器中的三個參數為：Kp= 0.41，Ki= 0.001，Kd= 0.31，可以看出，Kp在初始階段，有大幅度的上升，用來加快系統的響應，此時Ki明顯增大, 改善了系統穩態性能，系統慢慢趨于穩定，相應的Kd也明顯加大，用來改善控制系統的動態性能，縮短調整時間。從輸出曲線上來看，系統的超調量為2%，調節時間ts=0.13s，系統在t=0.2s時，輸出能準確地跟蹤輸入信號，即經過0.2s，轉子能準確回復到平衡位置。

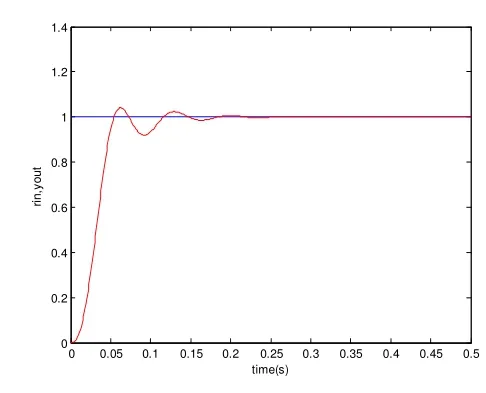
圖8 不加擾動時的系統輸出

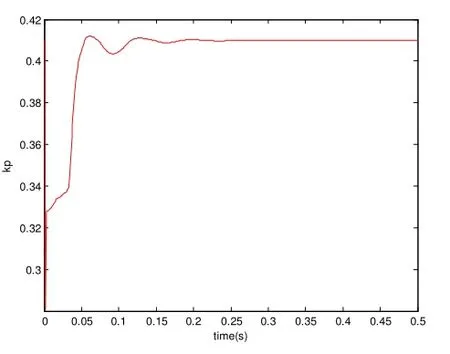
圖9 Kp的整定曲線

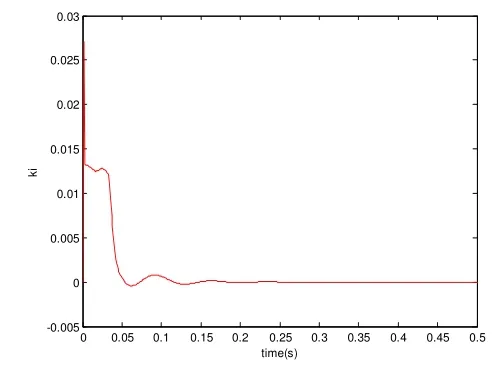
圖10 Ki的整定曲線

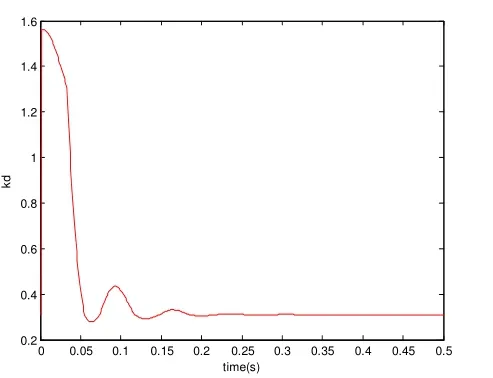
圖11 Kd的整定曲線

在t = 0.4s時，給系統加一幅值為0.5的擾動信號，系統的輸出如圖12所示。

從圖12可以看出，當系統受到擾動時，模糊控制器能迅速做出反應，并在線調整PID控制器的三個參數 Kp、Ki和Kd，使其達到最優，系統經過0.04s就可以抑制干擾信號的影響，使轉子快速的回復到平衡位置。主動磁懸浮控制系統的抗干擾能力明顯增強，系統具有較好的動靜態特性。

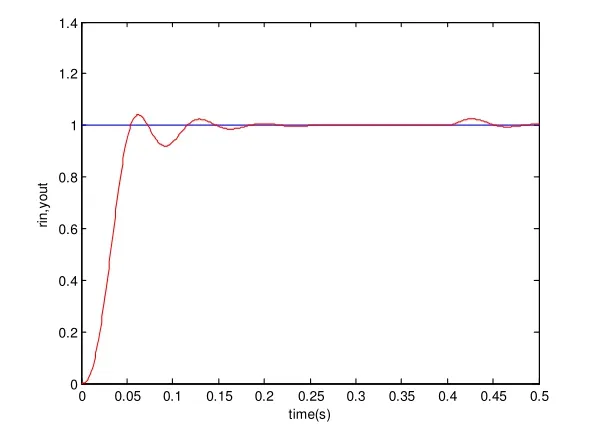
圖12 加入擾動后的系統輸出

4 結束語

以主動磁懸浮控制系統為控制對象，根據主動磁懸浮系統的非線性、參數不確定等特點，針對普遍應用的PID控制器中參數難整定的問題，設計了模糊自適應PID控制器，并進行實時控制及結果分析。首先，對主動磁懸浮控制系統的結構及工作原理進行了介紹并建立了主動磁懸浮控制系統開環系統的模型；然后設計了模糊自適應PID控制器；最后，在模糊PID自適應控制器的實時控制下，對主動磁懸浮控制系統進行仿真和分析，設計的模糊自適應PID控制器能使得主動磁懸浮控制系統具有較好的動態特性和穩態特性。

[1] SHAM ELI E, KHAM ESEE M B,HU ISSOON J P.Nonlinear controller design for a magnetic levitation device[J].M icrosystem Technologies,2007,13(5):831- 835.

[2] 張小建.主動磁懸浮軸承數字控制系統的研究, 南京航空航天大學碩士論文,2002.

[3] 張靜,徐林.磁懸浮系統的模糊自適應PID控制[J].計算機應用,2009,29(6):329-334.

[4] 諸靜.模糊控制原理與應用 [M].北京:機械工業出版社,1995.

[5] 羅文廣,韓俊峰,蘭紅莉.基于M atlab(Simulink)語言的模糊控制系統研究高級仿真[J].計算機仿真,2001,18(3):15-16.

[6] 劉金琨.先進PID控制及其Matlab仿真[M].北京:電子工業出版社,2003.

[7] 彭輝,徐錦華,侯海良.模糊控制在磁懸浮球系統實時控制中的應用[J].控制工程.2009,16(3):278-281.