多種檢測目標下樣本容量設計的比較

羅 森，李 立，安 偉

（1.北京林業大學 經濟管理學院，北京 100083；2.中國檢驗檢疫科學研究院，北京 100123；3.中國科學院 生態環境研究中心，北京 100085）

0 引言

抽樣檢驗是指根據概率論與數理統計原理，從一批產品中隨機抽取少量產品作為樣本進行檢驗，據以判斷該批產品合格與不合格的檢驗過程[1]。由于產品數量和成本等方面的原因，對一批產品進行質量判定時很難進行全數檢驗，產品質量檢驗的結果很大程度上由抽取的樣本所決定[2]。而抽樣進行過程中，樣本容量的確定是一個重要的問題。理論上，樣本容量越大，代表總體越充分，調查精度越高[3]，但如果樣本容量過大，不僅會造成不必要的人力、物力、財力的浪費，加大調查成本，也會降低實施抽樣的可操作性；如果樣本容量過小，可能會因樣本缺乏代表性造成抽樣誤差增大，抽樣調查結果的可靠性將難以保障[4-7]。特別是在食品安全監控過程中，隨著檢測的化學物質的增加，監測的目標也隨之擴大，各監測目標就對應著不同的最優樣本容量。因此，合適的樣本容量計算方法對于多種檢測目標下的抽樣調查非常重要[3]。

概率論中的大數定律和中心極限定理為抽樣調查中樣本容量的確定奠定了理論基礎[8]。在簡單隨機抽樣的條件下，已知總體方差或總體成數并給定極限誤差和置信度的情況下，就可以計算出相應的樣本容量。歐盟委員會的農藥殘留監控體系中的抽樣數量計算方法，則以n重伯努利試驗為理論基礎[9]，該方法在已知總體不合格率并給定置信度的情況下，也可計算出相應的樣本容量。然而兩種方法在使用上存在很大差異，在同樣的不合格率和給定的置信度下卻計算出迥異的結果。

本文將在對比上述兩種方法的基本原理基礎上，根據監測數據，采用這兩種方法分別進行樣本容量計算，對結果進行分析比較，并據此討論根據不同的調查目標選擇最優樣本容量計算方法。

1 兩種樣本容量計算方法的比較

1.1 方法1

在簡單隨機重復抽樣的條件下，根據區間估計的相關知識，假設總體成數為P，樣本成數為p，則樣本成數的標準差為

只要n充分大，一般np＞＞5和n(1-p)＞＞5時[10]，根據中心極限定理，p近似服從正態分布N～(p,p(1-p)/n)。因此，構建標準化統計量Z

可知，在重復抽樣條件下，已知總體成數為P，給定抽樣極限誤差及概率保證程度，則至少應該抽取的樣本容量為

其中，n表示樣本單位數；Δp表示抽樣極限誤差（最大允許誤差）；Zα/2表示在顯著水平為α時，標準正態分布在α/2處的臨界值。這里需要注意的是，計算結果需要向上取整。

從公式我們不難看出，影響樣本容量大小的兩個主要因素是極限誤差Δp和統計量Zα/2，而統計量Zα/2又由顯著性水平α和置信度來決定。極限誤差越小，樣本容量就越大；置信度水平越高，樣本容量就越大[3-6,11,12]。

1.2 方法2

根據n重伯努利試驗和二項分布的有關知識，若n次取樣中每次取到的不合格品的概率為p，則至少檢測出一個不合格樣品的概率為

歐盟委員會2002/63/EC指令歐盟農藥殘留監控體系中規定，為確保樣本在所檢查的貨物/商品中具有典型性，取樣須按照委員會指令2002/63/EC(EC,2002)確立的農藥殘留官方控制方法進行，按公式

計算確定抽樣樣本容量[13]。

2 兩種方法的比較實證

我們給定總體的不合格率，并分別設定置信度為90%、95%、99%，方法1的允許誤差為5%，運用方法1和方法2分別計算相應的樣本容量，結果如表1。

表1 不同參數下兩種方法的樣本容量計算結果

表1給出了兩種方法計算出的樣本容量在各個不同置信度下隨不合格率變化而變化的結果。方法1的計算結果趨近于正態分布，樣本容量極大值出現在不合格率為50%處。方法2計算的樣本容量隨著不合格率的下降而逐漸增加，尤其是在不合格率小于1后出現陡增。在同樣的置信度下，隨著不合格率的增加，兩種方法計算的樣本容量有著明顯的差異。分別抽取表1中兩種方法在95%置信度下計算出的樣本容量數，如圖1。

圖1 不同合格率95%置信度下兩種方法計算所得樣本容量

兩種方法最大的不同是方法1中存在極限誤差[14]，極限誤差是對抽樣估計的誤差范圍提出的要求，其確定一般需要具體問題具體分析，需要根據經驗或試驗分析后給出[15]。當實際超標率很低時，我們通常認為其合格；反之，實際超標率很高時，通常認為不合格。因此，當檢出率為50%時，我們很難判斷其是否合格，此時判斷合格的不確定性最高。方法1由于要求調查的目標結果在允許的誤差范圍內，所允許的誤差越小，則需要的樣本容量越大；方法2的應用目的在于“至少檢測出一個不合格樣品”，也就是說檢出即是不合格，所以方法2中的不合格率應指的是實際檢測中的超標率。如表1，隨著超標率的降低，則檢出至少一個不合格品所需要的樣本容量也就越大。

以上分析可以看出，兩種方法計算出的樣本容量大小有明顯區別，也存在著不同的適用條件。方法1對應著檢出率和容許的誤差精度，更適用于我國出口食品質量監測。目前發達國家為了控制食品安全，在進出口食品貿易中設置許多技術貿易壁壘[16]，因此我們有必要在出口食品檢測中嚴格把關，針對出口國設置的技術貿易壁壘有效控制我國出口食品的質量安全，防患于未然，避免遭受不必要的經濟損失。方法2對應著超限率，更適用于我國進口食品質量監測。在同一批次樣品中只需檢出一個不合格品即可拒絕整批貨物，用方法2可以使我們在抽取很少樣本的情況下達到監測進口食品安全的目的，將大大提高管理效率。

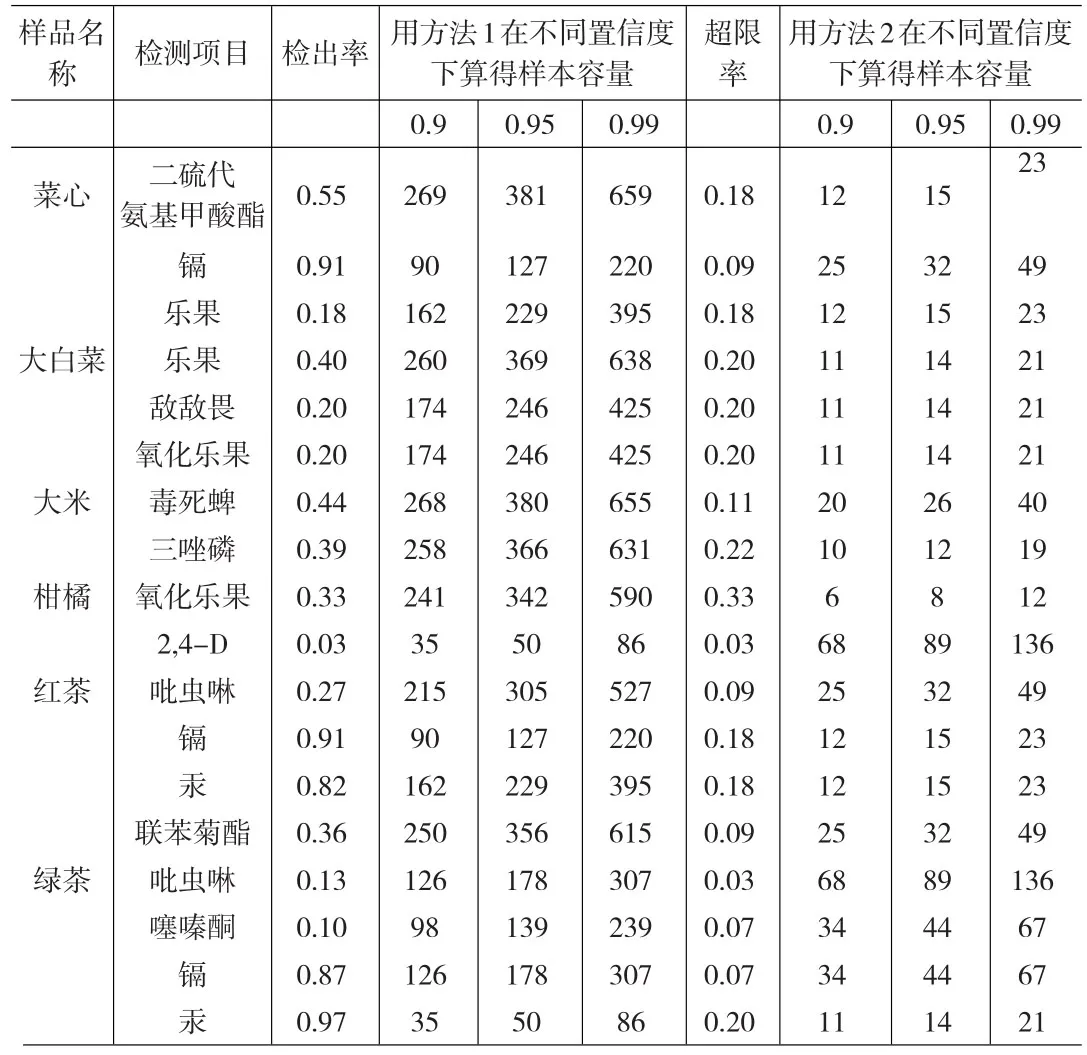
表2 按各樣品檢測項目檢出率和超限率計算所得樣本容量

為了對上述兩種方法所計算的結果有更加直觀的認識，這里根據地方管理部門對部分進出口樣品農藥和重金屬的監測數據，計算相應的樣本容量，如表2。

由表2可以看出，多種目標下每一個檢測項目的檢出率和超限率都會對應得出一個樣本量，在保證最高置信度的條件下采取取大原則[15]，即將抽樣調查的樣本容量確定為所有樣本容量需要值中的最大值，這樣做可以滿足所有指標對抽樣誤差的要求。將表2數據根據取大原則進行處理，如表3。

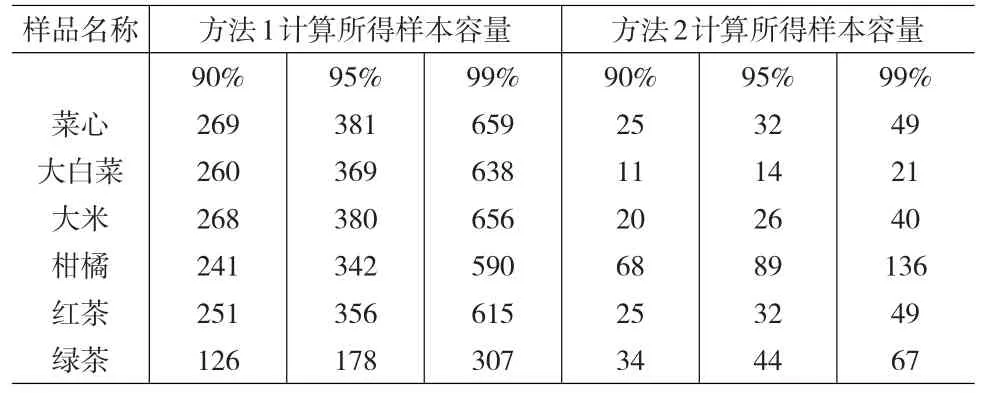
表3 各樣品在不同置信區間下最終應取樣本容量

以表3中菜心為例，通常，95%置信度下，如果一批菜心需要出口，則該批次的菜心應該抽取381個樣本進行檢驗；如果一批菜心需要進口，則該批次的菜心應抽取32個樣本進行檢驗。

3 結論

我們分析了兩種樣本容量計算方法的原理，并采用進出口食品的農藥和重金屬監測為目標案例計算了進出口食品的樣本容量。但這兩種方法并不能解決所有的問題。比如，以往的監測數據顯示該樣品的所有檢查目標檢出率為0%或100%，則這兩種方法都不能計算出應該抽取的樣本容量，這種情況樣本容量如何確定仍待進一步研究和討論。另外，本文所討論的兩種方法是在小范圍內實施的樣本容量確定方法，如何將這些方法合理的運用到不同層次的抽樣監測當中，也是仍需研究的問題。

[1]劉苗苗,寧尚勇,云振宇等.我國乳制品抽樣方法及標準現狀分析[J].農產品加工(學刊),2010,(3).

[2]盧鳳華.產品質量檢驗抽樣方法研究[J].科技致富向導,2011,(21).

[3]賀建風,劉建平.多指標抽樣的樣本容量設計方法[J].統計與決策,2008,(17).

[4]紀利霞.抽樣調查中樣本容量設計[J].山西大同大學學報(自然科學版),2009,(3).

[5]李良.抽樣調查中樣本容量的計算[J].科技經濟市場,2009,(9).

[6]李鵬祥.隨機抽樣中必要樣本容量的確定[J].赤峰學院學報(自然科學版),2009,(9).

[7]劉愛芹.隨機抽樣中樣本容量確定的影響因素分析[J].山東財政學院學報,2006,(5).

[8]張國友.關于抽樣調查中樣本容量的確定[J].安徽理工大學學報(社會科學版),2003,(1).

[9]茆詩松,程依明,濮曉龍編著.概率論與數理統計教程[M].北京:高等教育出版社,2011.

[10]陳在余,陶應虎編著.統計學原理與實務[M].北京:清華大學出版社,2009.

[11]薛長青.淺談影響樣本容量大小的因素和對調查誤差的認識[J].工業技術經濟,2001,(4).

[12]李永娣.統計推斷中樣本容量的確定問題[J].河南省情與統計,2000,(8).

[13]Commission E,Others.Commission Directive 2002/63/EC of 11 July 2002 Establishing Community Methods of Sampling for the Official Control of Pesticide Residues in and on Products of Plant and Ani?mal Crigin and Repealing Directive 79/700/EEC[Z].EEC,2002.

[14]WilliamMendenhall美,TerrySincich著美,梁馮珍4等.統計學[M].北京:機械工業出版社,2009.

[15]陳克明,寧震霖.市場調查中樣本容量的確定[J].中國統計,2005,(3).

[16]聶雪梅,儲曉剛,李立等.進出口食品安全問題、趨勢及改善初探[J].食品科技,2010,(1).