基于混合連接函數的最小方差套期保值研究

黃爭臻，段元萍

(上海理工大學a.管理學院；b.經濟與貿易研究所，上海 200093)

0 問題的提出

套期保值研究的主要內容在于套期保值比率的確定問題。傳統的套期保值理論直接采用套期保值比率為1的套保方案，這種方法的缺點是不能對風險與收益等套期保值的目標進行控制，因而適用面很窄。在追求最優化的現代理論基礎之上，套期保值理論開始關注對套期保值比率的選擇，一個合適的比率有可能得到比傳統方法更為有效的結套保果，這也是研究的意義所在。

現有的研究模型主要有兩類：一類主要關注降低風險，如最小方差套期保值模型[1]；而另一類在關注風險的同時也考慮組合資產收益，如均值方差套期保值模型[2,3]。

本文主要考慮降低套期保值者的風險，即單獨從風險的角度來分析套期保值行為，故選擇最小方差套期保值模型來進行研究。現有的基于最小方差的套期保值模型的研究主要問題有兩個方面。一方面是對于收益率序列的相互關系上，現有的研究只是利用某單一Copula函數來推導中位數相關系數，忽略了Copula函數對兩序列的擬合效果的分析，因此本文結合了阿基米德族的三種Copula模型的優點以及選擇偏向上下尾的分位數相關系數來針對收益率波動異常劇烈時期的套期保值問題闡述其合理性。另一方面是對兩收益率序列的模型建立上可以改進，用GARCH-t模型來代替以往的GARCH-normal來更好的描述金融時間序列的厚尾特征。

本文以農產品期貨品種為例通過實證分析計算套期保值比率，并且與其他傳統模型比較套期保值績效來驗證本模型的優越性。

1 最小方差套期保值模型

假設要給Ts單位的某現貨資產進行套期保值，構造的套期保值資產組合包括Ts單位多頭現貨頭寸與Tf單位空頭期貨頭寸，t時刻單位現貨價格為St，單位期貨頭寸價格為Ft，忽略保證金與交易費用等因素，至t+1時刻的套保資產組合收益率有：

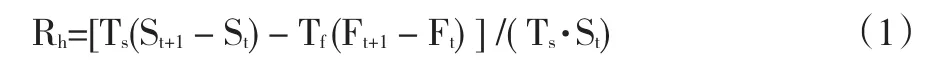
令Rs與Rf分別為現貨市場與期貨市場的收益率，即

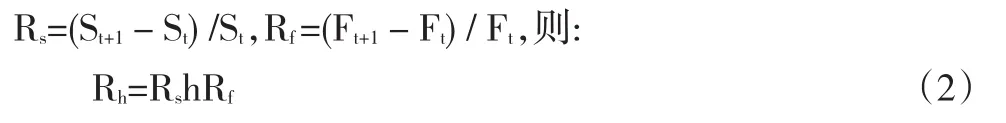
對式（3）取h的二階導數

其中ρ為現貨收益率與期貨收益率的相關系數。由式（6）可以看出，利用最小方差套期保值模型計算最優套期保值比率需要進行兩方面的估計，一是對期貨收益率與現貨收益率的標準差進行估計，二是對期貨收益率與現貨收益率序列的相關系數進行估計。

2 建立模型

2.1 相關系數的確定方法

在相關系數的選擇方面，許多研究利用到了Copula中位數相關系數來描述兩收益率序列的相關性，但如果近期期貨與現貨收益率波動劇烈，應用中位數相關系數會缺乏針對性，原因是中位數相關系數即包括了尾部相關的信息，也包括了收益率存在小波動情況下的相關性。如果將分位點往極端移動，度量這種情況下兩收益率序列的一致性，并且將其應用到套期保值模型之中來應對近期收益率波動異常劇烈的情況，將得到更好的套期保值績效。

選擇分位點為α與1-α的分位數，得到收益率序列同時高于α或低于1-α分位數的一致性度量指標：

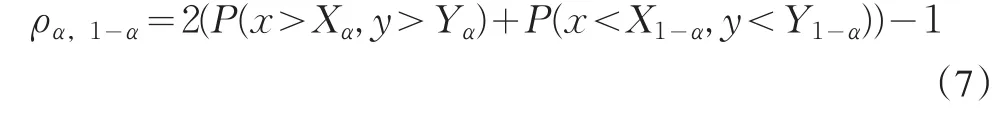
劇烈波動時宜采用偏高的分位點以恰當的反映高波動情況下的相關性，用基于此相關性度量而得到的套期保值比率來集中應對劇烈波動對組合資產收益率的影響。同樣的，相關性的分位數測度也可以轉化為利用Copula函數求解：

2.2 邊緣分布GARCH模型

在計算兩收益率序列的標準差方面，實證研究發現，在套期保值之前的歷史數據的標準差與套期保值期間的標準差有很大差異[4]，通過引入GARCH模型可以有效的處理標準差的時變性，實現套期保值模型的動態性。而GARCH-t更是對GARCH-normal模型的改進。通過構造一個二元的Copula-GARCH模型，可以完成對邊緣分布的擬合，并且通過GARCH模型對收益率序列的波動進行向前預測，另外連接函數可以完成對邊緣分布的相關結構的描述，從而通過本模型，完成對最小方差套期保值模型的求解。二元Copula-GARCH-t模型表示為：

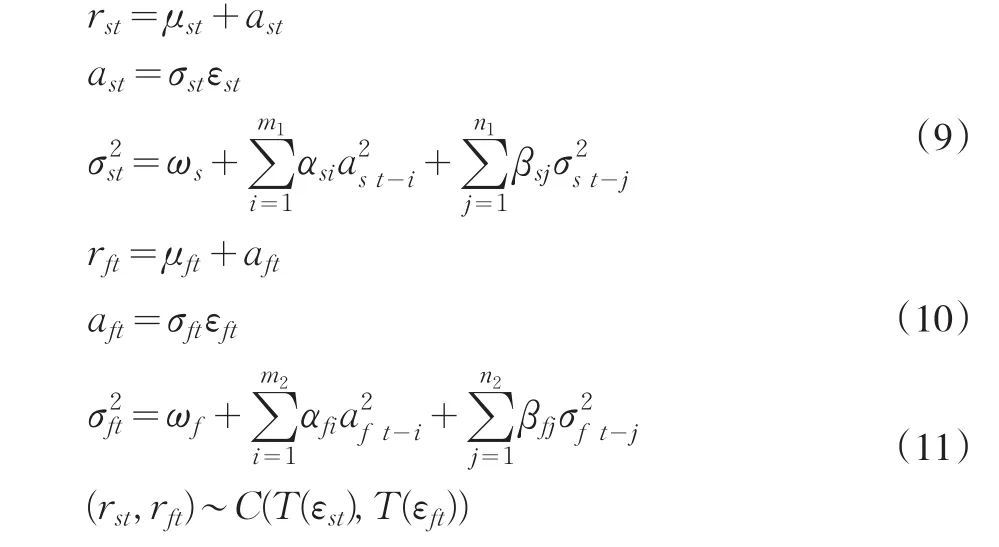
其中式（9）與式（10）分別為對現貨與期貨收益率建立的GARCH(m,n)-t模型，一般假設其中的ε服從正態分布或者標準化的學生t分布以及廣義誤差分布，通過添加一個動態方程來修正波動從而刻畫資產收益率的條件方差的時變特性。另外式（11）表示為用Copula函數對現貨與期貨收益率建立的聯合分布，由于Copula函數對隨機變量作單調增變換而不變，因此有：Cε=Cr

于是，我們用概率積分變換的方法來處理邊緣收益率序列，所謂概率積分變換是指：用隨機變量的密度函數對隨機變量進行積分變換，得到一列新的時間序列，其取值范圍符合連接函數的輸入要求。

2.3 Copula模型的選擇

由于金融序列的相關關系的復雜性，一個簡單的Copula函數難以將序列間的相關性描述得很透徹，因此，一種更加靈活的Copula函數隨之誕生，即混合Copula函數（M-Copula函數），通過構造一個Frank、Gumbel、Clayton三個Copula函數的線性組合：

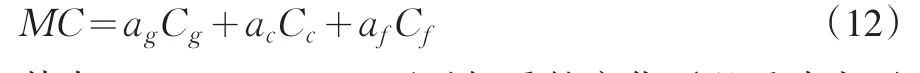
其中ag+ac+af=1，通過權重的變化可以反映出不同的相關模式，優點在于它包含了以上三種Copula函數各自的特性，在描述相關性時更為有效。

3 套期保值績效定義與評比方法

本文采用的套期保值績效采用Ederington(1979)給出的套期保值績效量化指標[5]，其定義為：參與套期保值與不參與套期保值相比，收益方差的減少程度。指標度量了套期保值之后對風險的降低程度，基于本文從風險這一角度進行套期保值研究，該績效指標恰好體現了這一出發點。本文的評比方法是通過橫向與縱向的比較來觀察不同模型的績效。

（1）橫向的對比，比較混合Copula與三種單一Copula模型在套保績效上的優劣，結果將體現出混合Copula函數在描述期貨與現貨價格波動關系上的有優異性。第二，比較基于兩種不同分位數相關系數的套期保值績效。

（2）縱向的對比，通過比較市場價格波動平緩與波動劇烈的情況下，傳統套期保值模型與Copula模型的套期保值績效，來體現基于Copula模型計算的相關系數在處理市場價格波動劇烈的情況下的良好性質。

4 中國農產品期貨的實證分析

本文采用鄭州商品交易所于2011年11月交割的棉花期貨價格數據與國內棉花現貨價格數據進行套期保值分析。具體來說，棉花期貨數據采用棉花期貨CF111從2010年11月15日至2011年11月14日共計246個交易日的期貨當日結算價；棉花現貨價格采用中國棉花信息網統計的與期貨價格同時期的每日棉花現貨價格數據。其中前180組數據被看做套期保值之前的歷史數據來進行模型的估計，后66組數據所在期間視為套期保值期間。

4.1 計算收益率波動值

首先根據期貨與現貨收益率的自相關與偏自相關情況，對期貨和現貨收益率模型誤差項進行ARCH效應檢驗的結果，發現AR模型殘差平方具有異方差性，可以在此基礎上建立GARCH模型。

選取棉花期貨合約的交易日期貨合約價格Pf與同種產品的每日現貨價格Ps，對數收益率乘以100放大數據可以提高后續計算的精度，構造對數收益率如下：

首先按照式（13）將所有價格數據進行處理之后得到收益率序列，再對期貨收益率序列建立GARCH-t模型參數估計結果如下：

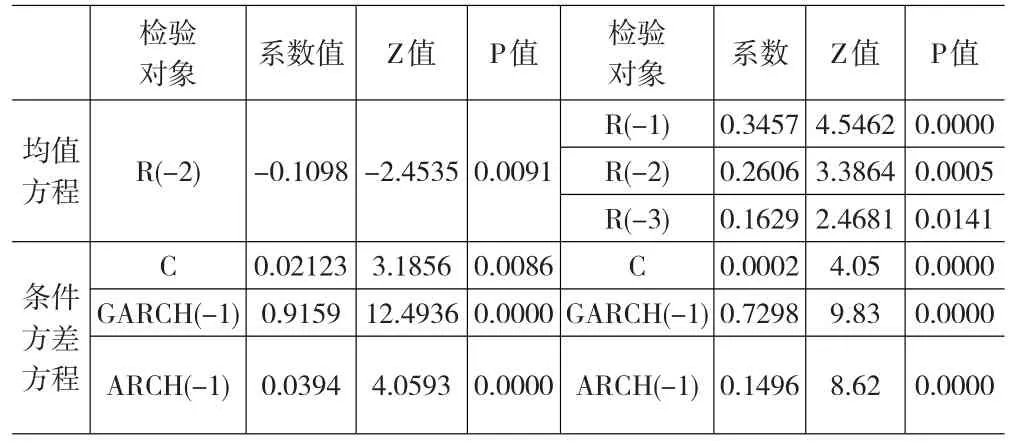
表1 GARCH模型參數檢驗表

如表1所示各參數估計值的概率值在0.05的顯著性水平下均通過檢驗，因此估計出的兩個模型各系數均具有顯著性。隨后的ARCH效應檢驗F與LM統計量對應概率均大于0.8，即消除了AR模型誤差項的異方差性。于是，可以直接利用估計出的GARCH模型的GARCH方程得到：σf=0.05356，σs=0.06866

由于Copula模型對輸入樣本的要求，利用已經建立好的期貨與現貨收益率序列的GARCH模型，依靠MATLAB對收益率序列進行概率積分變換，對變換后的序列進行K-S檢驗結果見表2。由結果可知，檢驗結果不能拒絕原假設，能夠繼續建立Copula模型。

表2 序列的均勻分布檢驗結果

4.2 計算相關系數

4.2.1 Copula模型的參數估計及擬合優度評價

估計混合Copula模型的參數，如式（12）所示，由于混合Copula參數較多，其極大似然函數比較復雜，不能用一般的方法進行參數估計，因此借助Matlab采用EM算法來進行估計。結果及擬合優度檢驗結果見表3。

表3 Copula模型參數估計結果

表3中各參數估計值在0.05水平下均顯著。由進行擬合優度檢驗得到的M統計量值122.45小于對應自由度的卡方分布分位數，因此通過檢驗，認為該Copula模型對實際分布的擬合效果理想。

4.2.2 基于Copula模型的相關系數與套期保值比率的計算

由于觀察到所采用的收益率數據波動比較明顯，因此在偏向尾部的相關系數的選擇上嘗試采用α=0.7，按照式（7）與式（8）所示，計算中位數相關系數與α分位數相關系數，將已估計出的參數以及對收益率序列進行概率積分變換之后的序列代入式中，相關系數ρ0.5,0.5=0.6980，ρ0.7,0.3=0.6773

根據最小方差套期保值比率的計算公式（6），將期貨、現貨收益率標準差以及相關系數代入，分別得到基于α分位數相關系數的最優套期保值比h1=0.8682與基于中位數相關系數的最優套期保值比h2=0.8948。

4.3 套期保值績效分析

4.3.1 基于M-Copula-GARCH的套期保值績效

以基于α=0.7的分位數相關系數計算的最優套期保值比率h1進行套期保值交易，對2011年8月13日之后的數據對套期保值進行績效分析，績效度量指標為式Ederington給出的套期保值績效量化指標HP，反應組合資產相對于不進行套期保值而言，使收益方差的減少程度。計算結果為HP1=0.6524228。另外計算基于中位數相關系數的套期保值績效記為HP2=0.6109731。

4.3.2 基于其他套期保值模型的套期保值績效

（1）完全套期保值模型：本模型完全不考慮歷史數據，直接用1作為套期保值比率，其套期保值績效記為HP3=0.4347362。

（2）線性回歸套期保值模型：本模型直接對套期保值之前的歷史數據采用最小二乘法作回歸，采用回歸系數作為最優套期保值比率，回歸系數為1.1826，計算得到套期保值績效結果為HP4=0.3725177。

（3）傳統最小方差套期保值模型：本模型的最優套期保值比率計算式與本文采用的計算式相同，同為式（6），不同之處是其中的相關系數采用的是歷史數據的線性相關系數，兩個收益率的標準差直接采用歷史數據的標準差，其計算結果HP5=0.3195228。

4.3.3 績效評比與結果

表4 套期保值績效比較

通過縱向比較發現，基于M-Copula-GARCH的最優套期保值模型得到了最優的績效，買入了較少的期貨頭寸，卻更好的屏蔽了風險，這種功效源于模型對數據關系的更貼切的分析與描述。而線性回歸套期保值與傳統的最小方差模型的套期保值績效甚至不如最簡單的完全套期保值，這是由于特定收益率序列的選擇導致序列之間的非線性相關關系占據了主要地位導致線性模型失效。橫向對比基于兩種不同的分位數相關系數的方法，當數據的波動比較大的時候，基于偏向尾部的相關系數得到了稍好的套期保值績效。同時混合Copula模型提高了分布的擬合效果。

因此，通過本研究的模型進行套期保值提高了套期保值績效，能有效的規避現貨市場的風險。

5 小結

第一，本文對農產品期貨與現貨收益率建立起了M-Copula-GARCH模型，通過實證分析驗證了其描述序列及序列之間相關性的理想效果。第二，利用Copula模型對期貨與現貨收益率擬合聯合分布，在模型的選擇上進行了擇優，從而使得到的相關系數比起傳統的線性相關系數有了很大的改進。第三，收益率的方差采用GARCH-t模型估計，改進之處主要體現在其動態性上；而相關系數則利用到了Copula模型在描述非線性相關上的優勢，采用了相對中位數相關系數更優的α分位數相關系數。第四，對比不同的模型，綜合橫向與縱向的評比結果來體現本研究方法更好的套保效果。

[1]Ederington,L.H.The Hedging Performance of the New Futures Mar?kets[J].Journal of Finane,1979,(34).

[2]David H.Risk,Futures Pricing,and the Organization of Production in Commodity Markets[J].Journal of Political Economy,1988,(96).

[3]Holmes P.Exante Hedge Ratios and the Hedging Effectiveness of the FTSE-100 Stock Index Futures Contracts[J].Applied Economic Let?ters,1995,(2).

[4]仇曉光，周穎.基于協整理論的期貨套期保值決策模型研究[D].大連理工大學,2008.

[5]Ederington,L.H.The Hedging Performance of the New Futures Mar?kets[J].Journal of Finane,1979,(34).