基于拓展貝葉斯決策模型的云計算類企業財務風險實證

廖 陽

（廈門大學 管理學院,福建 廈門 361005）

1 拓展貝葉斯決策模型構建

1.1 關鍵指標確定

為了完成對上市公司的財務風險模型研究工作，我們首先需要確定關鍵指標[1]過反復論證，我們最終選擇一下九個指標作為關鍵指標，它們依次為：營業收入、凈利潤、總資產、所有者權益合計(包含少數股東權益)、營業成本、銷售費用、管理費用、財務費用、投資收益。由于研究對象為具有同樣性質的企業，它們在九個具體指標上的數據存在差異，無法進行對應的橫向比較，因此，我們采用標準化的方法，對其預處理。即采用某對象的某年的某個具體指標數據除以該對象同年的總資產數據，得到標準化處理后的指標項數據。

1.2 隸屬度模型構建

按照模糊數學的理論，經濟領域的各種指標的發展不能用0或者1來衡量，而應采用隸屬度函數[2]性處理。該函數具有性質(1)：

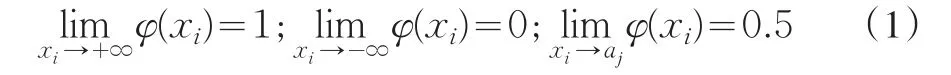
說明：xi為第i個指標項對應的數據；φ(xi)為第i個指標項取值xi時對應的隸屬度；aj為第i個指標項的“中點”。

考慮到上市公司發展的兩級性，ST公司、非ST公司。這兩類公司在業務發展中，各項指標數據可能會在一個較大的數值區間內變動。因為無法限定其具體的變化區間，我們不妨將其指標項數據取值區間延拓到整個實數軸上，即認為任意一個指標項X∈(-∞,+∞)，這樣我們就確定了指標項的取值范圍。接下來，我們需要確定隸屬度的取值范圍，參照公式（1），我們知道隸屬度的取值范圍為φ(X)∈[0,1]。目前已知的函數族中，反正切函數是滿足這種取值與映射要求的。基于以上理論，我們自主構建了符合上市公司發展特征的隸屬度函數，其具體形式如（2）：

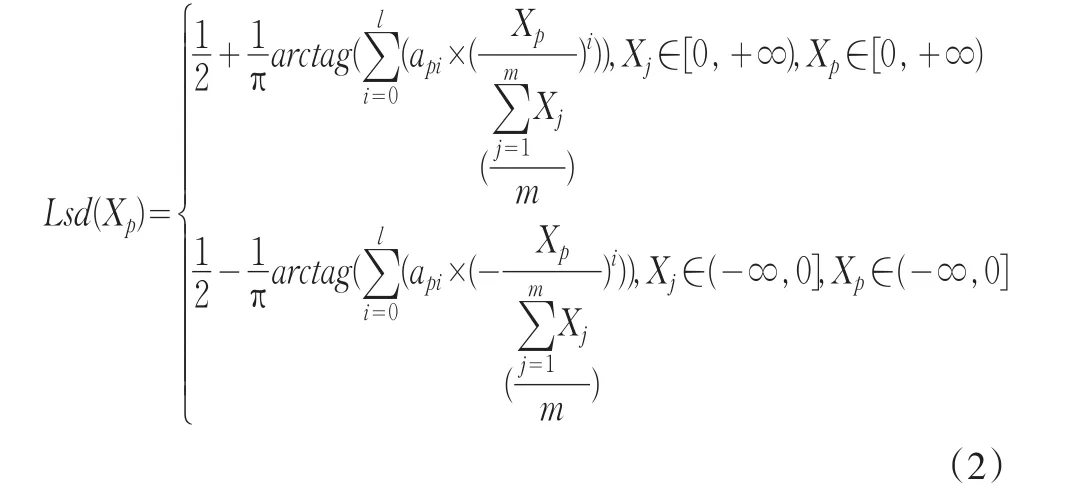
說明：Xp代表具體的指標數據；Lsd(Xp)代表該數據對應的隸屬度；Xj代表同指標下的所有數據，其數據總項數由m決定；api為對應的i階貢獻系數，階數的取值范圍為i∈[0,l]；arctag代表反正切函數。

另一方面，就隸屬度而言，其具體的取值是由其自身數值的特性決定（3）：

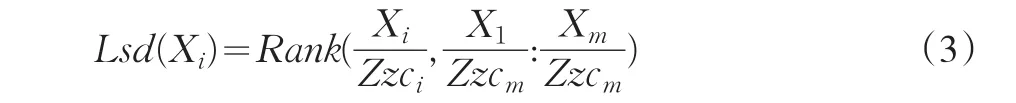
說明：Xj代表具體對象的某個指標在i年的數據；Zzci代表具體對象在i年的總資產；Rank為求序（正向序）函數，具體計算具體對象的某個指標的相對權重（）在整個時間序列中的排位。

結合公式（2）與公式（3）我們即可確定具體對象的某個指標項的隸屬度關系，具體參見（4）：

從公式（4）可以看出，目前還需確定的參數只有每一階的貢獻系數（api）和總的階數（l）。

對于這兩個未知參數，我們對公式(4)先進行正切變化，得到（5）：

對于公式(5)，我們利用計量經濟的分析方法，采用最小二乘法進行回歸分析，即可確定在一定的置信度范圍內的最佳階數（l）和對應的每一階的最佳貢獻系數（api）。

完成上述隸屬度函數的確定后，我們就可以確定概率與條件概率的具體數值。

1.3 概率空間的分解

對于每一個指標，我們可以將其所在的空間劃分為任意個不相交的子空間[3]，其劃分方法具體見（6）：

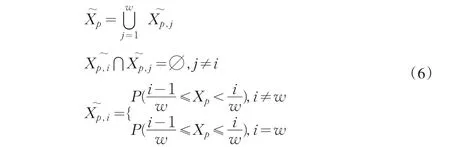
說明：Xp代表具體的某個指標數據；代表由某個指標數據決定的子概率空間；代表子概率空間的第i個子概率空間；w代表對子概率空間的平均劃分數量。

利用公式(6)的劃分方法，我們可以將整個概率空間劃分為7個一級概率子空間和對應的若干個二級概率子空間，其具體劃分方法如（7）：

通過論證，我們即確定了對一個概率空間的具體劃分，下面我們將采用這種劃分方法進行貝葉斯概率確定。

1.4 貝葉斯概率確定

在此，我們將采用前述的分析方法，來確定貝葉斯概率[4]公式的具體實現。按照貝葉斯概率公式，有公式（8）成立：

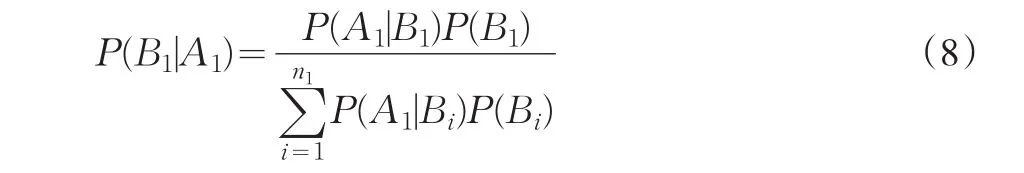
說明：P(B1|A1)代表事件A1發生時，事件B1發生的概率；P(A1|Bi)代表事件Bi發生時，事件A1發生的概率；P(Bi)代表事件Bi發生的概率。

針對該公式，以及前述的概率空間劃分，我們就可以得到針對上市公司的風險概率模型，其具體表述如（9）：

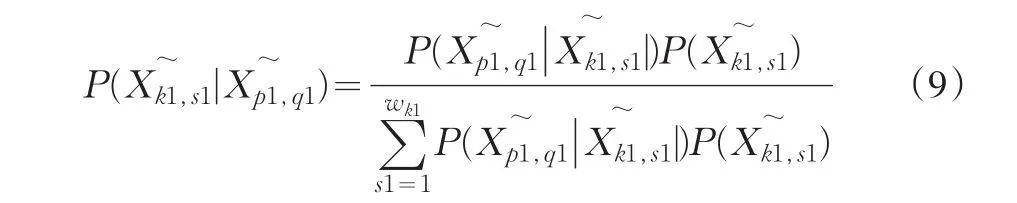
利用該公式，我們即可確定在不同的隸屬度情形下的事件發生的概率，具體說來就是確定不同的指標情形下的公司財務風險概率。

2 實證研究

2.1 基于關鍵指標的基礎調研與宏觀分析

在此，我們就實證對象的選取以及具體的指標數據選取進行確定，并在此基礎上展開對應的基礎調研與宏觀分析。

在此，我們選定了在國內上市的35家云計算類型企業中的12家作為實證對象展開研究，這12家企業的股票代碼依次為：600756、600770、600797、600804、600850、000021、 000063、 000066、 000070、 000836、 000938、000977。與此同時，我們確定了9個指標項作為測度項，它們依次為：營業收入、凈利潤、總資產、所有者權益合計(包含少數股東權益)、營業成本、銷售費用、管理費用、財務費用、投資收益。

通過查閱相關資料，我們確定了調查的時間范圍為2001年1季度至2012年3季度，對于上述企業，取自在該時間段內的最長可行時間范圍展開調查。通過深入調研，我們最終確定了上述對象在2001年1季度至2012年3季度的9個關鍵指標的具體數據。由于數據量較大，無法一一展示，現僅對其中的關鍵數據進行隸屬度變化展示。隸屬度的具體計算采用公式（3）的計算方法。由此，我們將這12家企業的隸屬度變化分圖展示，具體見圖1、圖2所示。

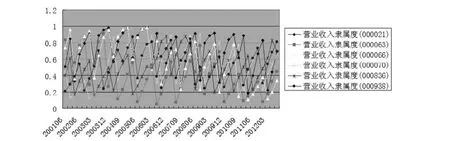
圖1 營業收入隸屬度變化圖

從圖1中可以看出，股票代碼為000021、000063、000066的離散營業收入隸屬度呈現穩步下行的趨勢，而股票代碼為000070、000836、000938的離散營業收入隸屬度則呈現出類似[0,π]區間的正弦函數變化，其變化規律類似于倒置的V字形。最高峰出現在發展中期，最低峰則出現在發展初期和發展末期。

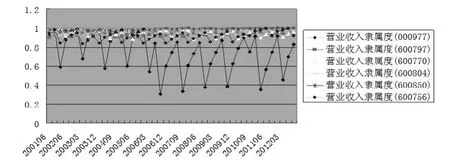
圖2 營業收入隸屬度變化

從圖2中可以看出，股票代碼為600797、600770、600804、600850、600756的離散營業收入隸屬度呈現出平穩發展的態勢，股票代碼為000977的應用隸屬度則呈現出小幅波動式下行的發展態勢。

通過上述宏觀分析，我們只能單個分析其變化形態，對于每種指標對應的對總體指標的影響方式和影響強度等深入問題，是無法通過宏觀分析得到的。下面，我們就采用前述自主構建的模型分析框架進行深入研究。

2.2 針對關鍵指標的隸屬度計量模型構建

在此我們針對前述確定的研究對象在2001年1季度至2012年3季度的關鍵指標數據進行隸屬度計量模型[5,6]構造。由于總資產已經作為對數據均一化處理的指標數據，故在此不再對其進行隸屬度模型構建。由此，我們進行了八個指標的隸屬度模型構建，這八個指標依次為：營業收入、凈利潤、所有者權益合計(包含少數股東權益)、營業成本、銷售費用、管理費用、財務費用、投資收益。

考慮到文章篇幅所限，在此將八個模型歸一為一個模型表出，具體公式（10）：

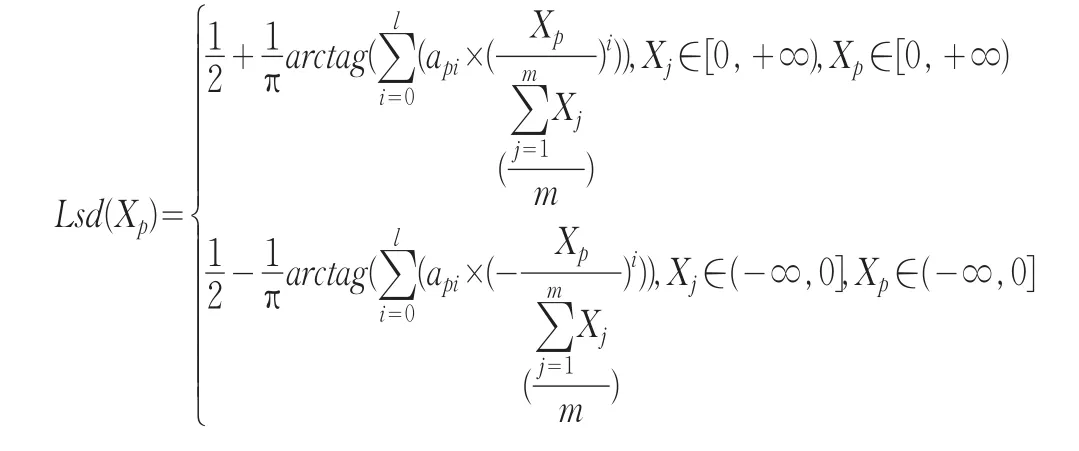
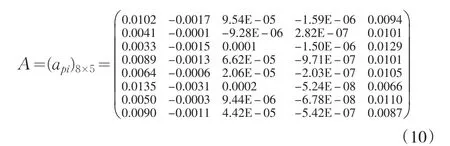
說明：矩陣A的第一行至第八行的數據依次為：營業收入的分階貢獻系數、凈利潤的分階貢獻系數、所有者權益合計(包含少數股東權益的分階貢獻系數、營業成本的分階貢獻系數、銷售費用的分階貢獻系數、管理費用的分階貢獻系數、財務費用的分階貢獻系數、投資收益的分階貢獻系數。

上述模型公式（10）所對應的可決系數與調整后的可決系數均在0.95之上，因此我們認為上述模型在統計學意義上是顯著的、可信的。由于該模型必須與后續的風險研究結合使用才能體現出功能，在此我們不再對其進行深入的論述。由此我們就確定了不同指標的隸屬度模型。下面，我們就利用該模型進行對應的財務風險研究。

2.3 基于隸屬度模型展開的財務風險研究

在此，我們就采用前述研究成果進行財務風險[7]研究。這里所說的財務風險是指基于歷史發展情形下，該公司以凈利潤為考核的隸屬度數據。具體地說，就是以上一年的各項指標（被總資產歸一化處理后的各項指標）所歸屬的不同的概率空間的前提下，得到的次年的凈利潤隸屬度數值（即對應的概率）。基于這一想法，我們采用前述研究中的公式（9）進行凈利潤隸屬度研究。整個實證研究過程完全按照前述的模型框架展開，在此不再贅述。將整體計算結果匯總，如表1所示。

從表 1可以清晰地看出，600756、600770、600797、600804、600850的凈利潤隸屬度均穩定在0.4左右，不會發生較大起伏。這說明上述五家企業次年的財務風險保持在一個較低的水平，不會發生重大問題。同時，我們也看到，000021、000063、000066的凈利潤隸屬度的歸屬區間基本為0.1附近，這說明上述3家公司的財務風險保持在一個較高的水平，需要高度關注，防止風險的擴大化、惡性化。同時，我們還看到，000070、000836、000938這三家企業的凈利潤隸屬度呈現出以區間[0.4,0.5]為中心的類正態分布特性，在其左右兩側為對稱性分布。這說明這三家企業的財務風險具有一定程度的波動性和突變型，需要有相應的財務預防措施，以防財務風險的突變和波動發生。最后，我們看到，000977的凈利潤隸屬度呈現以區間[0.4,0.5]為最高點的左單側遞減性特征，在區間[0,0.1]達到其左側的最低值，在區間[0.4,0.5]的右側則具有離散間斷落地性。這說明，000977的凈利潤隸屬度只可能逐步降低，不會逐步提高。也就是說，000977的財務風險只可能加劇，不可能改善。且其財務風險加劇的概率是逐步降低的。對于該企業必須在機制內部尋找原因，以便突破其現有的發展“陷阱”，提升該企業的平穩、安全、快速的自我循環能力。

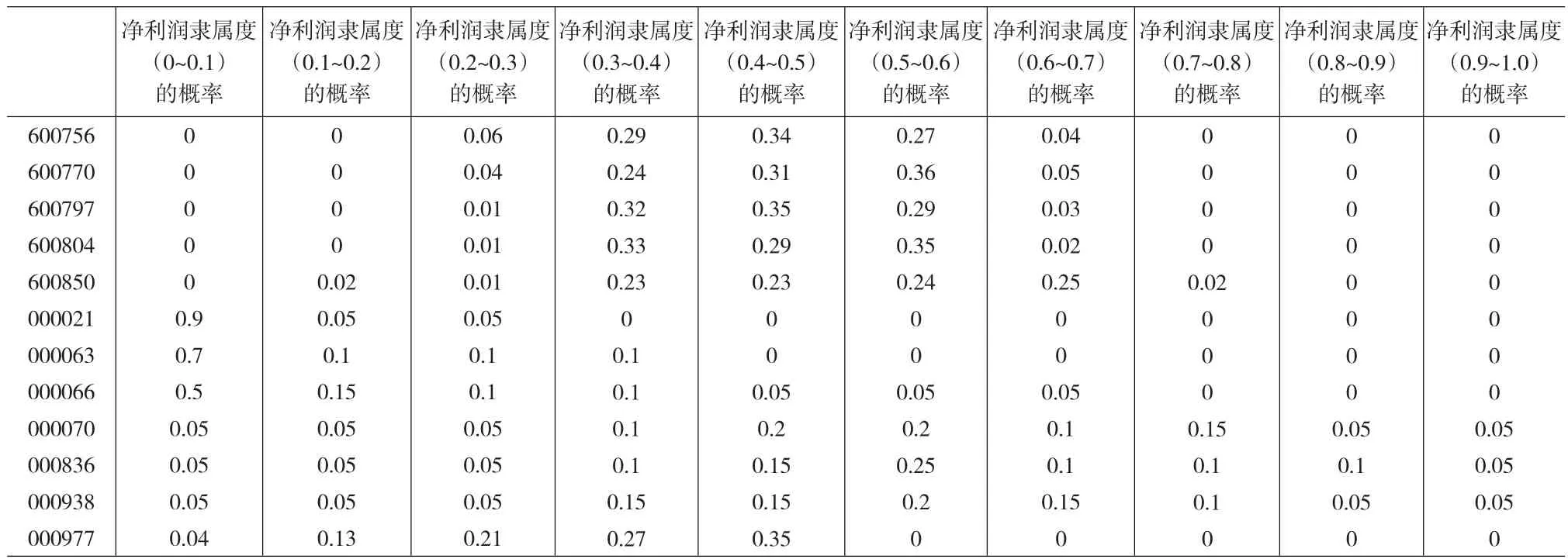
表1 以凈利潤考核的財務風險隸屬度歸屬表

3 結論

我們將模糊數學中的隸屬度理論應用到此次研究中，通過自主構建了符合企業發展的隸屬度模型，實現了對關鍵指標的離散轉連續化處理，并基于該模型進行了企業發展的概率空間的有效正交分解，從而將理論計算中的貝葉斯決策模型成功地拓展到實證企業發展風險研究中。之后，基于前述研究自主構建的理論模型，展開了實證研究。實證研究的對象為國內上市的云計算類企業，通過基礎調研獲取了研究所需的基礎資料，并針對這些基礎資料進行對應的宏觀分析。在此基礎上，將理論研究模型有效地應用于實證研究對象，得出了具體的風險研究結果。選定的實證對象的財務風險主要為三種，它們依次為：風險平穩型、風險惡化型、風險波動型。風險平穩型主要是指企業的財務風險處于一個相對恒定的區間，且該區間對應的風險值較低。風險惡化型主要是指企業的財務風險處于一個相對穩定的區間，且該區間的風險值較高。風險波動型主要是指企業的財務風險不在處于一個穩定的區間，變化幅度較大，且區間跨越性較顯著。針對這三類不同風險類型的企業，我們提出了三種不同的風險預警與處理措施。針對風險波動型企業要增加企業的風險流動資金，并啟動風險應急處理機制展開對應的處理。針對風險平穩型企業要增加企業的深入發展力度，推動企業的快速發展，針對風險惡化型企業，要對其展開實時監控，并啟動最高級別的風險處理機制，防止企業發展中出現極端甚至是崩潰現象的發生。通過上述實證分析，我們不僅形成了自主的風險預測管理模型，還基于該模型得到了有效的分析結果與解決對策。這一系列結果，是此次研究的最大收獲。

[1]黃福寧,聞岳春.影響創業板市場運營的關鍵要素——以AIM市場為例的研究[J].經濟管理,2011,(8).

[2]Dan E.Tamir,Lu Jin,Abraham Kandel.A New Interpretation of Complex Membership Grade[J].International Journal of Intelligent Systems,2011,26(4).

[3]Deok-Soo Kim,Joonghyun.Beta-decomposition for the Volume and Area of the Union of Three-dimensional Balls and Their Offsets[J].Journal of Computational Chemistry,2012,33(15).

[4]David Birkes,Yadolah Dodge.Bayesian Regression[Z].Alternative Methods of Regression,2011.

[5]沈悅,李善燊,馬續濤.VAR宏觀計量經濟模型的演變與最新發展——基于2011年諾貝爾經濟學獎得主Smis研究成果的拓展脈絡[J].數量經濟技術經濟研究,2012,(10).

[6]王裕雄,肖海峰.實證數學規劃模型在農業政策分析中的應用——兼與計量經濟學模型的比較[J].農業技術經濟,2012,(7).

[7]張海波,陳紅.人民幣匯率風險度量研究——基于不同持有期的VaR分析[J].宏觀經濟研究,2012,(12).