云環境下基于任務分類和LPM優化模型的調度算法

張以利，楊萬扣

0 引言

云計算是由分布式計算、并行計算、網格計算、虛擬技術等技術綜發展起來的新型計算模型。云環境下不乏許多經典調度算法。R.Armstrong提出將長度最小的任務調度到最優資源上的調度算法，可使任務完成數最大化，但算法未考慮任務重要程度及任務預算等市場效益約束問題。R.Buyya提出在用戶任務預算和期望完成時間約束下，優先調度在資源上執行時間較短的任務，算法充分考慮了任務預算等市場效益問題，但在任務預算不足或期望完成時間較短，云服務方無法保障任務全部完成的情況下，任務完成數會較小[1]。

針對用戶任務預算不足或期望完成時間較短，云服務方無法保障任務全部完成的情況下，提出基于任務分類和線性規劃優化模型調度算法（Scheduling Algorithm based on Task Classifying and Linear Pogramming Model in a Cloud Environment,SCLCE），使任務完成數最大化，同時考慮到任務的重要程度。SCLCE算法根據任務長短及重要性進行分類，然后建立任務計算資源關系矩陣及三個相關約束條件，以任務完成數最大化為目標函數，搭建線性規劃優化模型，同時給出算法實現[2]。

1 基于任務分類和LPM優化模型的調度算法

云計算環境中，設 n個任務構成集合 T=（T1,T2,…Ti…,Tn）(i∈n)；設 p 臺機器構成集合 M=（M1, M2,…M i…,M p）(i∈p)，這些機器提供m個計算資源，構成計算資源集合 R=（R1,R2,…Ri…,Rm）(i∈m)[3]。

1.1 相關概念定義及任務分類

定義1 計算資源

計算資源定義為一個三元組[4]，公式（1）計算資源的三個屬性分別為資源號屬性、資源計算性能屬性、資源計算價格屬性。

定義2 用戶任務

用戶任務定義為一個五元組，公式（2）

用戶任務的五個屬性分別為任務號屬性、任務類型屬性、任務長度屬性、任務預算屬性和用戶任務期望完成時間屬性。

用戶任務預算屬性budgT，為該任務按預期完成后所付給資源提供方的價格數[5],deadT為調度在某資源上的任務執行完成時間不得超過的時間值屬性。

定義3 TH任務集合 TL任務集合

typeT為任務類型屬性，分為High和Low兩種類型。High類型任務為比較重要的用戶任務或者是長度較短的任務，要求最遲要在時間deadT之前完成，這些任務構成TH任務集合,即 TH=(TH1,TH2,…THi。。。,THn) (i∈n)。而 Low類型任務為不是太重要的用戶任務，用戶期望完成時間也不是太高，可以延遲完成該任務，這些任務構成TL任務集合,即 TL=(TL1,TL2,…TLi…,TLm) (i∈m)。

SCLCE算法中，根據type屬性的不同，將所有任務分為兩個類型的集合TH和TL。將集合TH中任務調度到優秀的資源上，確保High類型任務優先完成，得到較高的用戶任務完成數[6]。

1.2 線性規劃優化模型調度策略

如果由于用戶任務預算不足或者任務期望完成時間較短，TH集合任務未全部完成，則SCLCE算法將該集合中未完成的任務類型typeT由High更改為Low，即將TH集合中沒有完成的任務加入到TL集合中。

在對TL集合任務進行調度時，采用基于LPM優化模型的調度算法，即通過一個線性規劃數學模型優化策略，在滿足三個約束條件下，以執行任務完成數最大化為目標，返回任務完成數及任務與資源的映射關系，從而得到資源分配最優解[7]

定義4 任務計算資源調度關系矩陣Anm

Anm定義為一個n′m的矩陣，公式（3）

其中，矩陣元素aij意義為：

該矩陣的元素值，反映任務Ti在計算資源Rj上的調度分配情況。

每個用戶任務最多只能調度到一個計算資源上，而每個計算資源可以根據需要調度多個任務在其中執行[8]，于是，根據式3可得到下面的約束條件，公式（4）

執行TL類型的任務時，設第j個計算資源執行TH類型任務共花費時間timeRj, 任務期望完成時間deadT，全部計算資源在執行TH類型任務所獲總成本為costSum，兩種類型任務的總預算為 budgSum，則剩下執行時間為 deadT-timeRj, 剩下可用預算為budgSum-costSum，于是，根據式3和式4，可得到下面的兩個約束條件[9]，公式（5）、（6）

其中，lengTi為第i任務Ti的長度，perfRj為第j個計算資源 Rj的計算性能，pricRj為第 j個計算資源 Rj的計算價格，Ti為第i個任務。式5是任務期望完成時間的約束條件，式6是用戶任務預算約束條件。

在SCLCE調度算法中，完成任務數最大值為：

式7是任務完成數的最大值，是SCLCE算法調度所期望的目標，即數學中的目標函數，式3、式5和式6，分別是用戶任務在資源上調度的約束條件、用戶任務期望完成時間的約束條件和用戶任務預算的約束條件。由此，線性規劃數學模型(LPM)建立如下：

約束條件：

LPM 優化模型是運籌學中解決有限資源最佳分配問題的數學模型，即如何對有限資源作出最佳方式的調配和最有效的利用，以使最充分地發揮資源的效能去獲取最佳的經濟效益[10]。LPM 求解，即在約束條件下使目標最優的一組變量的取值。

求解該數學模型，即在滿足三個約束條件下使得執行任務完成數最大化，返回任務完成數及任務與計算資源的映射情況，從而得到計算資源分配最優解。LMP優化模型調度算法策略，見算法1。

算法1 LPM優化模型調度算法

1.3 基于任務分類和線性規劃模型的調度算法

在云計算環境中，設有 n個計算資源的集合 R=（R1,R2,…Ri…,Rn）(i∈n)，m個任務的集合T=（T1,T2,…Ti…,Tm）(i∈m)。針對用戶任務預算不足或者用戶任務期望完成時間較短，資源提供方無法保障全部任務的順利完成，SCLCE算法采用基于任務分類和LPM優化模型的調度算法，確保重要類型任務優先完成并最大化用戶任務的完成數[11]。

假設任務在執行過程中是不可搶占的，并且對于任務類型typeT相同的任務，執行的優先級順序相同，則基于任務分類和LPM優化模型的調度策略，如算法2所示。

算法2 基于任務分類和LPM優化模型調度算法

2.仿真實驗及結果分析

仿真實驗：采用R.Buyya的CloudSim模擬平臺，這是一個使用云計算環境來模擬經濟模型的實驗平臺。本實驗使用5臺機器，M=（M1, M2, M3,M4,M5），每臺機器提供20個計算資源，這20個計算資源的計算性能、價格都相同，共有 100 個計算資源，R=（R1,R2,…Ri…,R100）(i∈100)，計算性能參數perfR用機器每秒執行指令數描述，預算及價格參數均用相對值描述。實驗設立100個任務，T=(T1,T2,…Ti。。。,Tn) (i∈100)[12]。

對比實驗：采用同 R.Buyya提出的經典調度算法作對比，記錄兩個算法實驗數據并圖示，通過對比分析 SCLCE算法的優劣。

共設計兩組實驗如下：

第一組實驗：驗證基于LPM優化模型的調度算法，實驗數據記錄如圖1所示。任務不分類，即只有HL任務。以任務預算和期望完成時間參數組合分 8個組且各組的組合參數數據逐漸增加：G1（20000,1000），G2（40000,2000），G3（60000,3000），G4（80000,4000），G5（100000,5000），G6（120000,6000），G7（140000,7000），G8（160000,8000）。

任務預算和期望完成時間參數組合與任務完成數的關系，如圖1所示：

圖1 基于LPM優化模型的調度算法驗證模擬實驗

實驗分析：由圖1可看出，SCLCE算法的數據線總是在經典算法的上方。這是因為前者采用LPM優化模型調度策略，即在任務預算不足或期望完成時間較短而云服務方無法保障任務全部完成條件下，以任務完成數最大化為目標函數，所以會得到最大化的任務完成數；而后者雖然充分考慮了任務預算等市場效益問題，但在同樣約束條件下，任務完成數會較小。

第二組實驗：驗證基于任務分類的SCLCE算法，實驗數據記錄如圖2和圖3所示。用戶任務根據typeT類型屬性的High和Low分為TH集合和TL集合，不斷變化的TH集合任務數為橫軸， TH任務完成數或總任務完成數為縱軸。

TH集合中的任務數隨TH任務完成數的變化情況，如圖2所示。

實驗分析：由圖2所示：

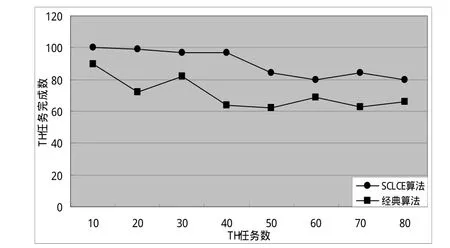
圖2 TH集合任務數隨TH任務完成數的變化情況

可看出，SCLCE算法數據線總在經典算法的上方，這是因為前者采用任務分類并優先考慮的策略，根據任務長短及重要程度分成TH和TL集合，對TH集合中的任務優先調度，而后者則對任務重要性未做充分考慮。

TH集合中的任務數隨總任務完成數的變化情況，如圖3所示：

圖3 TH集合任務數隨總任務完成數的變化情況

實驗分析：由圖3可看出，SCLCE算法數據線在50之前始終處于經典算法數據線上方，而在50之后則明顯放緩甚至有的數據點還在經典算法線的下方。這是因為，SCLCE算法采用任務分類且優先調度TH任務的策略，在50之后，隨著TH任務占有率的快速增加，TH任務會占用大量優質資源，嚴重影響用戶任務全局優化。所以，SCLCE算法的任務分類時，TH任務數在整個任務中的百分數要適中，一般不要超過50%。

3.結束語

云環境下基于任務分類和線性規劃優化模型調度算法，是對R.Armstrong和R.Buyya提出的經典算法的有效改進。該算法充分考慮到用戶任務預算不足或期望完成時間較短，資源提供方未能全部完成的情況下，如何最大化用戶任務完成數的問題。同時還充分考慮到了用戶任務的重要程度及用戶任務預算等市場效益約束問題。

[1]劉曉茜.云計算數據中心結構及其調度機制研究[D].合肥:中國科學技術大學,2011.

[2]師雪霖，徐恪.云虛擬機資源分配的效用最大化模型[J].計算機學報, 2013 Vol.36 (02): 252—262.

[3]祝家鈺，肖丹，王飛.云計算下負載均衡的多維QoS約束任務調度機制 [J].計算機工程與應用, 2012 Vol.38 (14): 38-40.

[4]朱錦雷, 劉俊鵬.面向云計算的虛擬進程調度算法[J].計算機工程, 2012 Vol.38 (14): 38-40.

[5]左利云, 曹志波.云計算中調度問題研究綜述 [J].計算機應用研究, 2012,29(11):4023-4027.

[6]張春艷,劉清林,孟珂.基于蟻群優化算法的云計算任務分配[J].計算機應用, 2012,32(05): 1418-1420.

[7]景波,劉瑩,黃兵.基于遺傳算法的Job Shop調度問題研究[J].計算應用研究, 2013,30(3):688-691.

[8]白露 晏立.多處理器固定優先級算法的可調度性分析[J].計算機應用,2012 Vol.32 (03): 603-605.

[9]任豐玲, 于炯, 楊興耀.基于最小化傳輸和完成時間的多DAG調度[J].計算機工程, 2012 Vol.38 (23):287-290.

[10]鄒偉明,于炯,英昌甜,胡丹.基于動態等待時間閾值的延遲調度算法[J].計算機應用研究,2012,29(11):4073-4078.

[11]胡志剛, 劉艷.云環境下基于組合雙向拍賣的動態資源定價[J].計算機工程, 2012 Vol.38 (08): 19-21.

[12]王鵬 張磊 任超 郭又銘.云計算系統相空間分析模型及仿真研究[J].計算機學報,2013，Vol.36 (02): 286—296.