基于循環(huán)相關(guān)的GPS 信號捕獲

任 遠 羅丁利

(西安電子工程研究所 西安 710100)

0 引言

GPS 是美國在1973 年開始研制的衛(wèi)星導(dǎo)航與定位系統(tǒng)，具有高精度、全天候、全球覆蓋、方便靈活等特點。GPS 信號在傳輸過程中采用直接序列擴頻調(diào)制方式，接收機在時間信息提取和導(dǎo)航電文解調(diào)之前，需要實現(xiàn)載波和C/A 碼的二維同步［1］。載波同步和C/A 碼同步一般分為捕獲(粗同步)和跟蹤(精確同步)兩個階段，且GPS 衛(wèi)星信號的跟蹤需要以信號捕獲為前提。在信號跟蹤之前，接收機內(nèi)部復(fù)制的載波和C/A 碼信號必須與接收信號吻合到一定程度，估算出接收信號的載波多普勒頻移和碼相位，然后根據(jù)這些信號參數(shù)估計值初始化跟蹤環(huán)路，以幫助接收通道展開對信號的跟蹤。

傳統(tǒng)GPS 信號捕獲方法［1］對接收的衛(wèi)星信號在多普勒頻移域和碼相位域進行二維線性掃描式搜索，其優(yōu)點在于只需要少數(shù)幾個數(shù)字相關(guān)器，并且這些相關(guān)器隨后也可以用于信號跟蹤過程，簡化了硬件設(shè)計，其缺點是運算量大，捕獲時間較長。基于載波(或多普勒頻移)域的FFT 并行捕獲算法［2］將二維搜索變?yōu)榇a相位域上的一維搜索，該算法對多普勒頻移的估算精度取決于離散傅里葉變換的數(shù)據(jù)長度和數(shù)據(jù)的采樣頻率，使用短時間數(shù)據(jù)進行運算時多。普勒頻移分辨率不高，導(dǎo)致信號捕獲靈敏度性能變差，而使用長時間數(shù)據(jù)進行運算時在提高多普勒頻移分辨率的同時也使FFT 點數(shù)增多，運算量增大。基于碼相位域的FFT 并行捕獲算法［3］將信號搜索變?yōu)槎嗥绽疹l移域上的一維搜索，大幅度提高了捕獲速度。文獻［4］在基于碼相位域的FFT 并行捕獲算法基礎(chǔ)上，用傅里葉系數(shù)的循環(huán)移位取代頻率補償和FFT 運算，繼而將運算量較之原始算法減少一半。基于FFT 的并行捕獲算法要求信號采樣率為2 的冪次，一般的GPS 信號采樣率較難滿足，這就增加了計算復(fù)雜度而影響處理速度。文獻［5］中介紹了一種基于平均采樣技術(shù)的捕獲算法，將FFT 數(shù)據(jù)點數(shù)重采樣到2 的冪次點，減少了運算時間，也降低了硬件實現(xiàn)的難度和成本。

本文介紹了一種基于循環(huán)相關(guān)的捕獲算法，與傳統(tǒng)的線性搜索捕獲算法相比，減少了運算量，同時保留硬件設(shè)計簡單、數(shù)字相關(guān)器可用于后續(xù)信號跟蹤過程等優(yōu)點。

1 傳統(tǒng)線性搜索捕獲算法［6］

假設(shè)接收機接收到的GPS 信號經(jīng)過射頻前端處理之后可表示為:

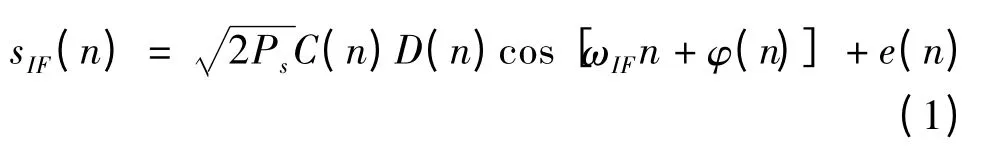
式中PS是信號功率;C(n)是C/A 碼，其值為± 1;D(n)是比特率50bps 的導(dǎo)航電文;ωIF是中頻載波頻率，其值由射頻前端和多普勒頻移決定;φ(n)是初始載波相位;e(n)為零均值高斯白噪聲。

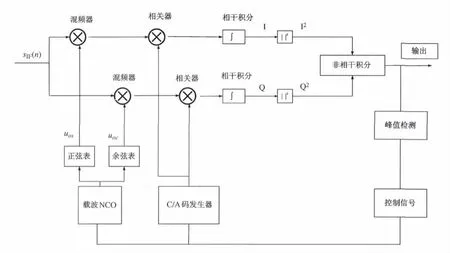
圖1 線性搜索捕獲原理

圖1 給出了GPS 接收機線性搜索捕獲算法的基本流程。本文以接收一顆衛(wèi)星信號為例，在捕獲過程中，數(shù)字中頻信號sIF首先分別與同相支路的本地正弦和正交支路的本地余弦復(fù)制載波進行混頻，然后混頻結(jié)果與復(fù)制C/A 碼進行相關(guān)，接著相關(guān)結(jié)果i 與q 經(jīng)過時間為Tcoh的相干積分后生成數(shù)據(jù)對I和Q，

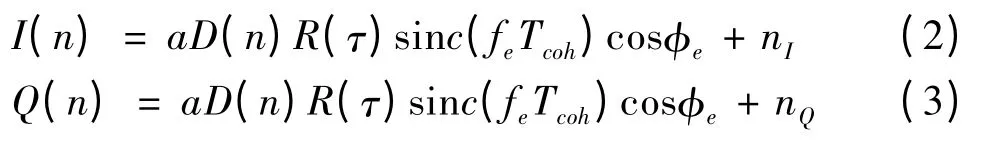
其中，a 為信號幅值;τ 為C/A 碼相位與搜索碼相位之間的差異;fe為接收載波頻率與搜索頻率之間的差異;Φe為兩載波之間的相位差異;nI與nQ分別代表I 支路與Q 支路上均值為零且互不相關(guān)的高斯噪聲。

假設(shè)非相干積分數(shù)目為Nnc，最后經(jīng)非相干積分后得到非相干積分幅值V。

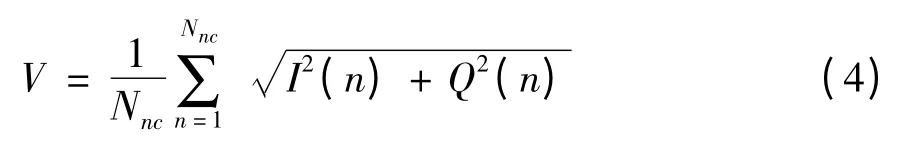
信號捕獲的非相干檢測法通過檢測非相干積分幅值V 的大小來判斷接收信號是否已經(jīng)被搜索到:若非相干積分幅值V 小于捕獲預(yù)先設(shè)置好的捕獲門限Vt，則信號尚未被搜索到，于是接收機按照既定的搜索步長調(diào)節(jié)載波數(shù)控振蕩器(NCO)和C/A 碼發(fā)生器輸出，繼續(xù)在下一個搜索單元進行搜索與檢測，直到確認信號成功捕獲。

2 基于循環(huán)相關(guān)的捕獲算法

2.1 算法原理

C/A 碼是周期為1023 個碼片的Gold 碼，碼率為fC/A=1.023Mcps，即在每個C/A 周期(1ms)有1023 個碼片，且具有良好的自相關(guān)和互相關(guān)特性［7］。一般情況下GPS 軟件接收機將接收信號從射頻前端輸出后進行中頻采樣，采樣頻率為fS，則一個C/A 碼片周期(1ms)對應(yīng)的采樣點數(shù)N=fS/1000，相應(yīng)的本地C/A 碼也被重采樣為N點。圖2 示出基于循環(huán)相關(guān)的捕獲算法流程，針對C/A 碼相關(guān)過程進行改進，具體實現(xiàn)方法分為兩步。

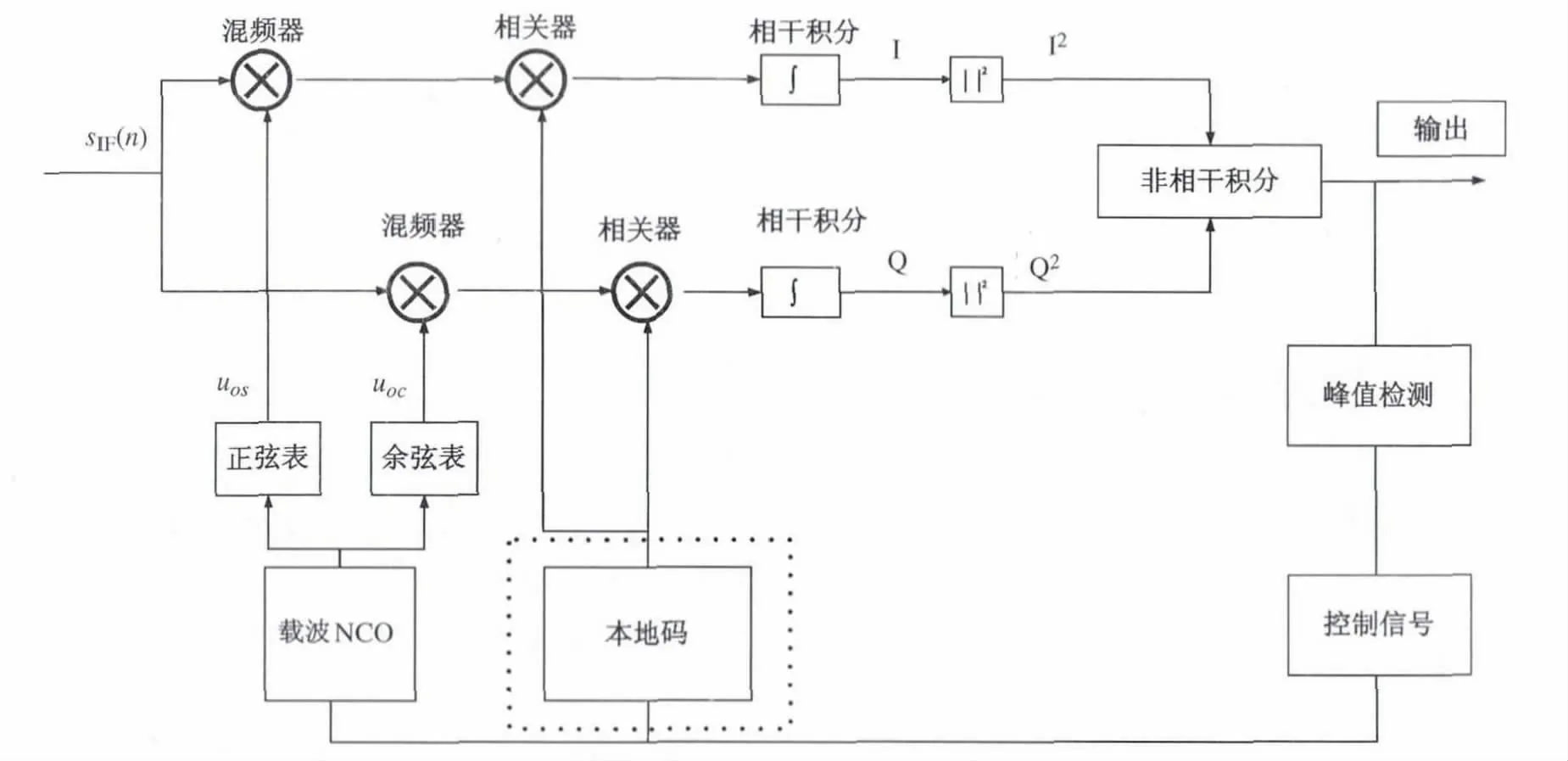
圖2 基于循環(huán)相關(guān)的捕獲算法流程圖

a.對于采樣后周期為N 的C/A 碼序列C(n)，假設(shè)接收信號序列為C(n +m)，m 為接收信號碼相位。本地C/A 碼發(fā)生器產(chǎn)生的C/A 碼為序列C(n)，按照圖3 所示循環(huán)移位后疊加構(gòu)成新本地碼序列h(n):

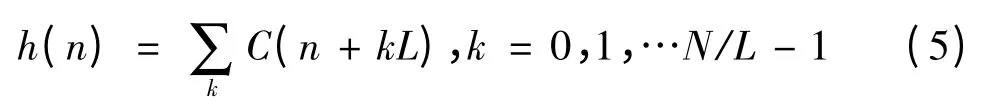
其中L 為每次循環(huán)移位點數(shù)，其取值將在3.2節(jié)中說明。為了方便公式推導(dǎo)，這里假設(shè)N 是L 的整數(shù)倍，實際情況下當N 不能被L 整除時，循環(huán)移位次數(shù)可以取N/L 的向上取整值。

將h(n)設(shè)為圖2 虛線框中的本地碼，接收信號c(n +m)與h(n)連續(xù)進行L 點循環(huán)相關(guān)運算，取模后結(jié)果為| R1(τ)|:

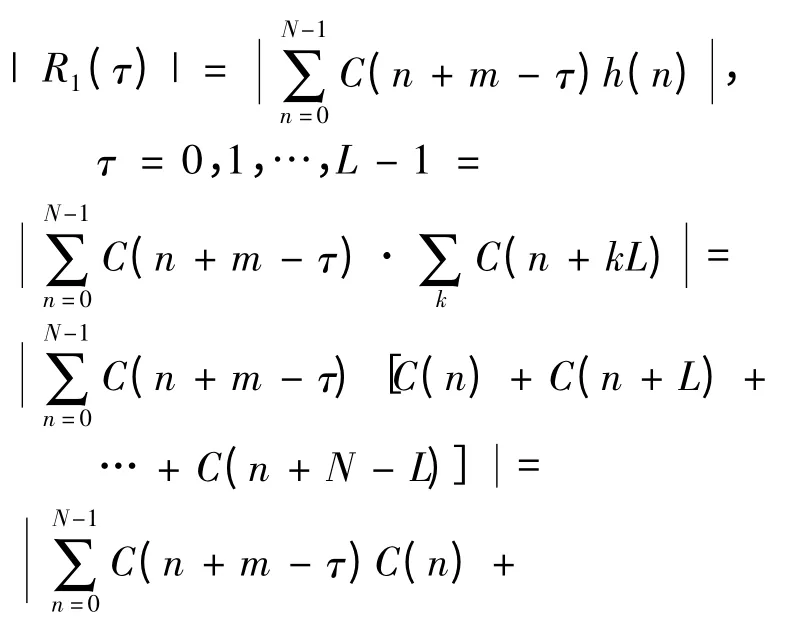
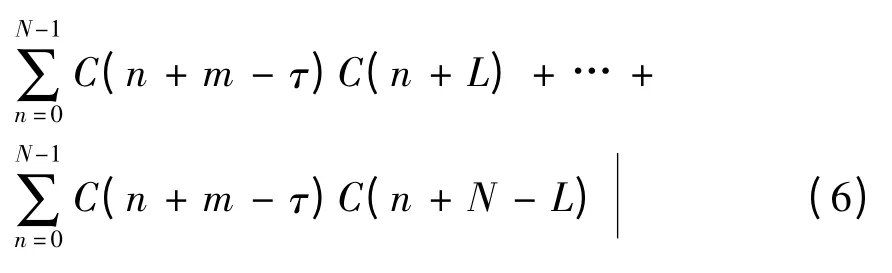
根據(jù)C/A 碼良好的自相關(guān)性特點，當m-τ=KL 時，式(6)中有且只有一項會達到最大相關(guān)值，其余項都很小，找出|R1(τ)|最大值對應(yīng)的τ。此時可以確認某GPS 衛(wèi)星信號的存在，只是得到的碼相位同步點存在若干個L 的模糊，即此時估算出的碼相位為相對碼相位，下一步確定接收信號的絕對碼相位。

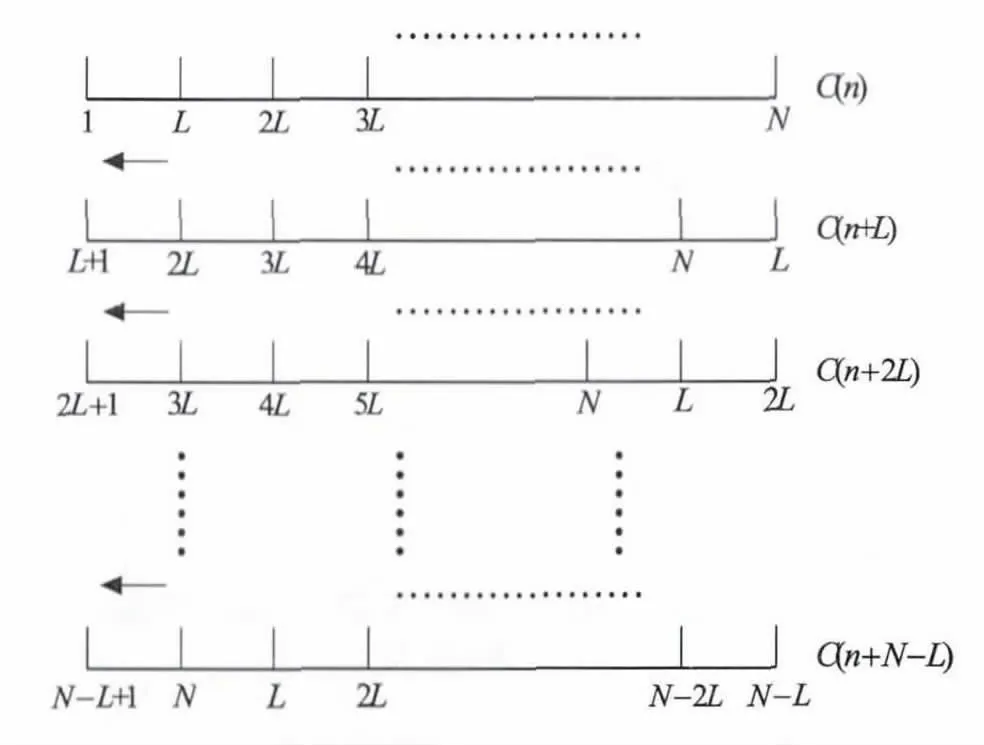
圖3 本地C/A 碼循環(huán)移位示意圖

b.將原始C/A 碼序列C(n)向左循環(huán)移位τ-1 個碼片后設(shè)為圖2 虛線框中的本地碼，本地碼與接收信號C(n+m)進行相關(guān)運算，對相關(guān)值取模后記錄其大小，然后本地碼向左循環(huán)移位L 個碼片再與接收信號C(n+m)進行相關(guān)取模運算，如此進行N/L-1 次移位和相關(guān)取模后找出N/L 個相關(guān)模值中最大值所對應(yīng)的循環(huán)移位次數(shù)K。最后計算出接收信號C/A 絕對碼相位:

2.2 計算量分析

基于循環(huán)相關(guān)的捕獲算法與傳統(tǒng)線性搜索捕獲算法相比，差別主要體現(xiàn)在相關(guān)運算的計算量上，而在多普勒頻移分辨率方面則完全一樣。

表1 運算量比較

從表1 中看出基于循環(huán)相關(guān)的捕獲算法運算量與一個C/A 碼片周期(1ms)對應(yīng)的采樣點數(shù)N、循環(huán)移位點數(shù)L 有關(guān)。當中頻采樣頻率fS較大時，即一個C/A 碼片周期(1ms)對應(yīng)的采樣點數(shù)N 較大情況下，基于循環(huán)相關(guān)的捕獲算法運算量減少更為可觀，節(jié)省了大量的捕獲時間。采樣頻率fS一定時，即一個C/A 碼片周期(1ms)對應(yīng)的采樣點數(shù)N 固定情況下，如果不考慮輸出信噪比因素，當L=N1/2時運算量最小。然而基于循環(huán)相關(guān)的捕獲算法構(gòu)成新本地碼之后進行相對碼相位搜索時，使噪聲分量相對于信號分量上升了N/L 倍，輸出信噪比SNR 下降，較少的循環(huán)移位點數(shù)使SNR 惡化更為明顯。

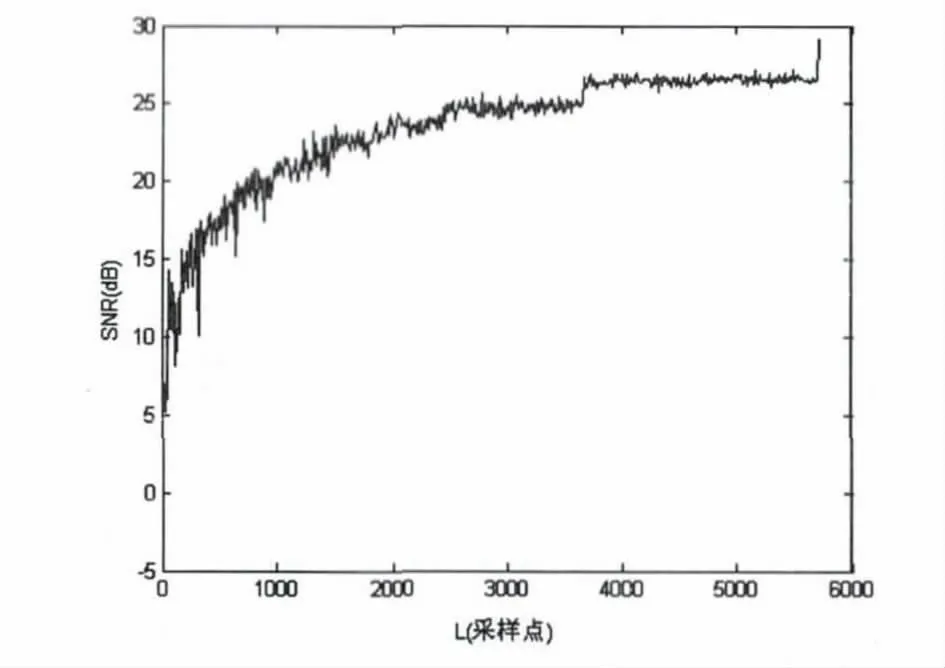
圖4 L 與輸出SNR 的關(guān)系

圖4 表示輸出信噪比SNR 與循環(huán)移位點數(shù)L的關(guān)系，SNR 曲線包絡(luò)隨著L 的增大而增大。在實際工程應(yīng)用中，根據(jù)對輸出信噪比和捕獲速度的要求來確定循環(huán)移位點數(shù)L，從而確定新本地碼的組成。

2.3 仿真與結(jié)果分析

實驗數(shù)據(jù)為實際采集的GPS 信號。采用Zarlink 公司產(chǎn)品GP2015 芯片的射頻前端，輸出中頻為1.405396MHz，采樣率fS為5.714MHz，一個C/A 碼片周期(1ms)對應(yīng)的采樣點數(shù)N=5714，本地C/A 碼也被重采樣為5714 點。本文使用Matlab 對采集到的數(shù)據(jù)進行仿真，捕獲第7 號衛(wèi)星信號。為了提高輸出信噪比，保證可靠的檢測概率，傳統(tǒng)線性搜索捕獲算法與基于循環(huán)相關(guān)捕獲算法都采用了9ms 長度的相干積分。

圖5 是運用線性搜索捕獲算法對7 號衛(wèi)星信號的捕獲結(jié)果。圖中峰值超過預(yù)先設(shè)定的門限，表明捕獲成功，多普勒頻移為-1400Hz，碼相位為第3573 個采樣點，運算量為2N2=65299592 次實數(shù)乘加運算。

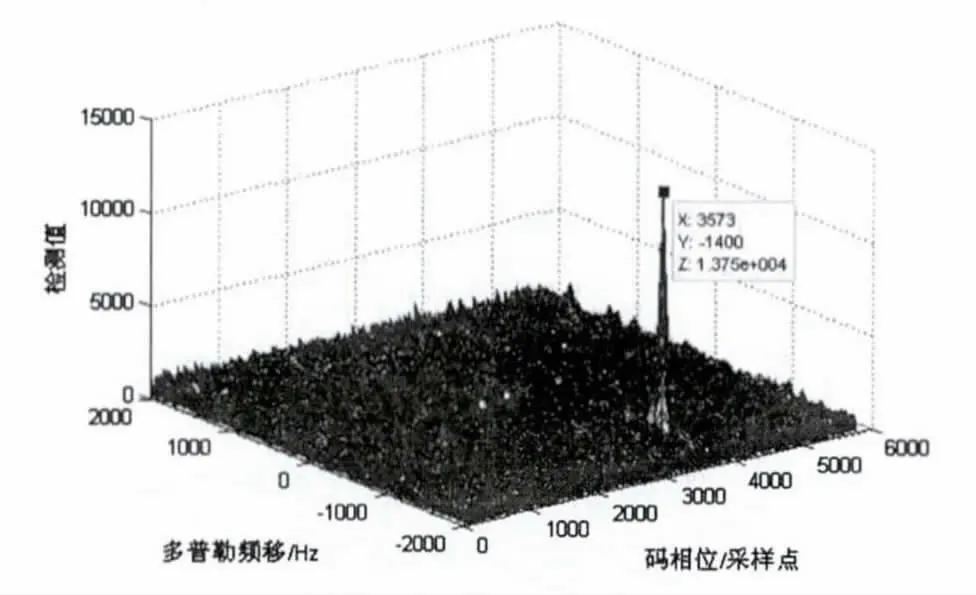
圖5 線性搜索捕獲結(jié)果

基于循環(huán)相關(guān)的捕獲算法仿真中，本地C/A 碼重采樣后按3.1 節(jié)方法構(gòu)成新本地碼時取循環(huán)移位點數(shù)為L=1143，對應(yīng)的循環(huán)移位次數(shù)為4。此時L的取值在輸出信噪比和算法計算量之間做了折中，既保證了較高的輸出信噪比，又大大減少了運算量。

圖6 是基于循環(huán)相關(guān)的捕獲算法對7 號衛(wèi)星信號的捕獲結(jié)果。圖中尖峰峰值超過預(yù)設(shè)定的門限，表明捕獲成功，多普勒頻移為-1400Hz，C/A 碼的相對碼相位為第144 個采樣點。

圖7 表示基于循環(huán)相關(guān)的捕獲算法第二步中循環(huán)移位次數(shù)和相關(guān)模值的關(guān)系。當循環(huán)移位次數(shù)為3 時，本地C/A 碼與接收信號相關(guān)值取模后遠遠大于其他相關(guān)模值。由3.1 節(jié)式(7)可估計絕對碼相位為第144 +3 ×1143=3573 個采樣點。

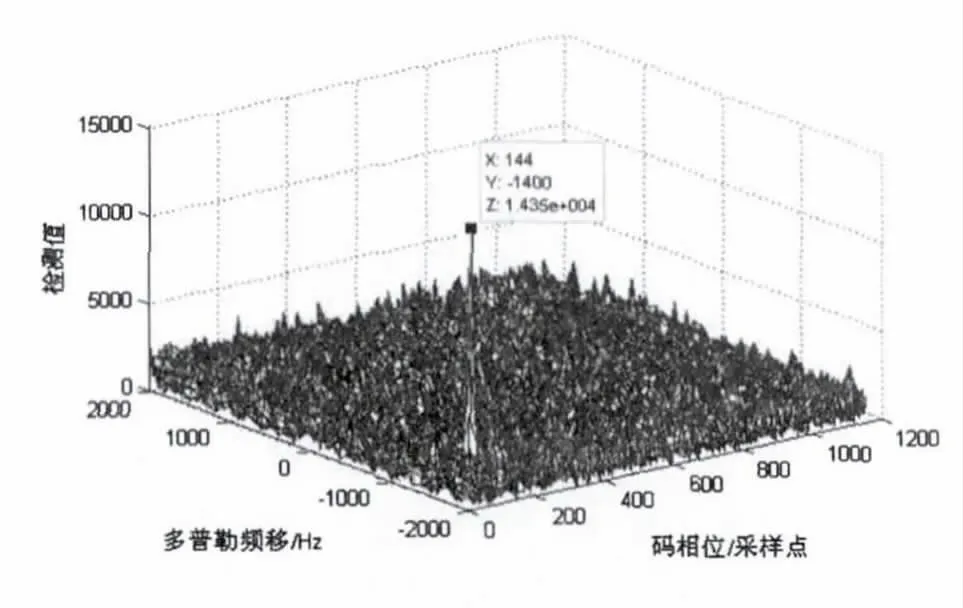
圖6 基于循環(huán)相關(guān)的捕獲結(jié)果

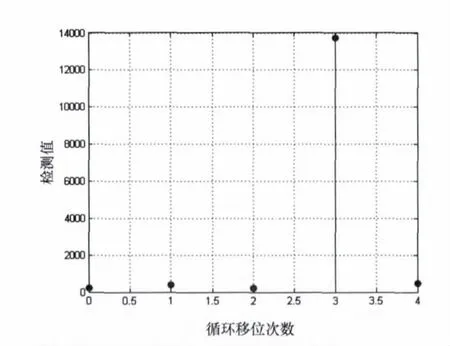
圖7 循環(huán)移位次數(shù)和相關(guān)模值關(guān)系圖

上述仿真結(jié)果與線性搜索捕獲算法仿真結(jié)果一致，驗證了基于循環(huán)相關(guān)捕獲算法的正確性，運算量為2(N/L+L)N≈13119344 實數(shù)乘加運算。基于循環(huán)相關(guān)的捕獲算法實數(shù)乘加運算大約只有線性搜索捕獲算法的五分之一，運算量顯著減小。

3 結(jié)論

本文討論了GPS 信號線性搜索捕獲算法實現(xiàn)，介紹了一種基于循環(huán)相關(guān)的捕獲算法，結(jié)合串行和并行捕獲方法，使運算量大大減少;硬件實現(xiàn)簡單，只需要若干個數(shù)字相關(guān)器，且這些相關(guān)器隨后可以用于信號跟蹤過程。通過對兩種算法仿真結(jié)果分析，驗證了新算法的正確性。在構(gòu)建本地新碼時應(yīng)該根據(jù)輸入信噪比，捕獲時間以及正確捕獲概率的要求，來確定循環(huán)移位點數(shù)L 的值。

［1］Kaplan E D.Understanding GPS principles and applications ［M］.Norwood，MA：Artech House，1996.

［2］Frai D M.A fast acquisition CDMA receiver for burst transmission system［C］.The 11th IEEE International Conference on ICECS，Sheraton Moriah Tel-Aviv，2004，342-345.

［3］Tang B，Liu S S，Tang W T.Design a L1 software receiver based on IF GPS signal simulator［C］.The 8th International Conference on Signal Processing，Beijing，2006.

［4］陳希，張銳，帥濤.基于FFT 的GPS 快速并行捕獲 算 法［J］.宇 航 學(xué) 報，2011，32 (1) ：162-166.

［5］曹單，汪澎，周建紅.GPS 快速捕獲算法與仿真［J］.火控雷達技術(shù)，2012，41(1) ：24-27.

［6］謝鋼.GPS 原理與接收機設(shè)計［M］.北京：電子工業(yè)出版社，2009.

［7］樊昌信等編.通信原理(第5 版) ［M］.北京國防工業(yè)出版社，2009.