用于彎曲型試樣斷裂韌性計算的COD轉換公式精解

姚 瑤，蔡力勛，包 陳

（西南交通大學力學與工程學院，四川 成都 610031）

0 引 言

Rice[1]于1968年提出了與積分路徑無關的參量——J積分，在彈塑性斷裂力學的發展中起到了非常重要的作用。采用J積分作為表示裂紋尖端應變集中特性的平均參量，避免了直接計算在裂紋尖端附近的彈塑性應力應變場。獲取斷裂韌性JIC的J阻力曲線所用塑性功Up需由載荷與加載線張開位移VLL的關系曲線得到。但是現廣泛應用于斷裂韌性測試中的FFCT（如圖1），即在裂紋嘴測量裂紋張開位移的CT試樣以及SEB（如圖2）均不能直接獲取其加載線/施力線位移。現行斷裂韌性測試規范[2-4]中并未提供FFCT及SEB試樣裂紋嘴張開位移V0與加載線/施力線裂紋張開位移VLL之間的轉換關系。美標ASTM E1921-2011[5]推薦采用比例系數0.73描述FFCT試樣VLL-V0轉換關系。蔡力勛等[6-7]基于臺階型CT試樣（load line compact tension，LLCT）和FFCT試樣的裂紋長度柔度計算式推導了裂尖小范圍屈服條件下FFCT試樣的VLL-V0換算公式；并依據相同的理論，給出了SEB試樣對應的彈性轉換公式。包陳、蔡力勛等[8]根據剛性轉動假設和功等效的方法，推導了FFCT試樣在裂紋面發生較大轉角時的VLL-V0轉換公式，石凱凱、蔡力勛[9]等依據SEB試樣轉動幾何關系推導了相應的彈塑性轉換公式，但該公式的精度還有待進行細化分析。本文基于彈塑性有限元（finite element analysis，FEA）精細網格計算，針對材料硬化以及轉動角度對FFCT和SEB試樣的COD轉換公式的影響進行了探討，從而對剛性轉動的有效性進行了驗證，并分別提出了FFCT試樣及SEB試樣更高精度的COD換算公式。

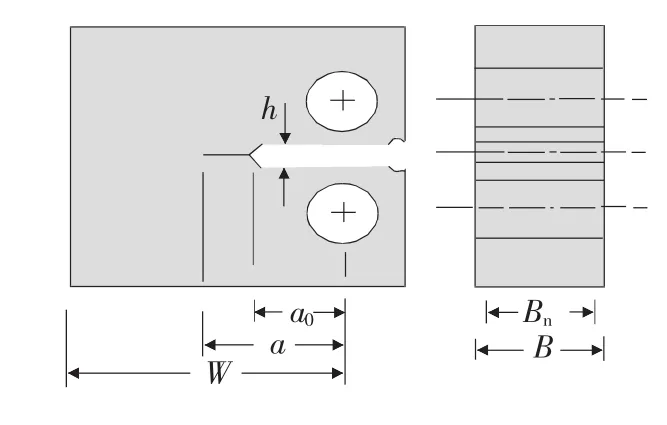
圖1 FFCT試樣

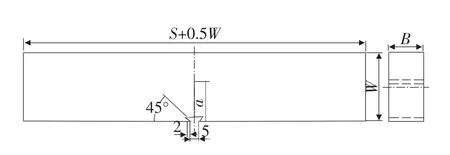
圖2 SEB試樣

1 有限元計算網格對精度的影響研究

單元網格的劃分在有限元仿真分析中是很重要的一個環節，結構關鍵部位的網格疏密程度直接影響了計算結果的精確程度。為了消除網格疏密程度對有限元計算結果的影響，現對不同裂尖網格密度進行對比計算。定義FFCT試樣和SEB試樣裂紋尖端約2 mm范圍內網格數量約為8 000時為一倍網格密度。在此基礎上對網格密度進行加密，分別對0.5倍、3倍、6倍、8倍、10倍、15倍及 20倍裂尖網格密度進行有限元計算。圖3所示分別為FFCT試樣和SEB試樣加載線/施力線張開位移VLL與20倍網格密度結果之間的相對誤差。可以看出，隨著裂尖網格密度的增加，兩種試樣的加載線張開位移VLL計算值趨于穩定，綜合考慮計算成本、結果精度等因素，選取8倍裂尖網格密度進行分析計算，兩種試樣的有限元模型如圖4所示。

2 有限元精細網格計算結果分析

對于符合冪律硬化特征的材料，其單軸本構關系可用Hollomon模型描述：

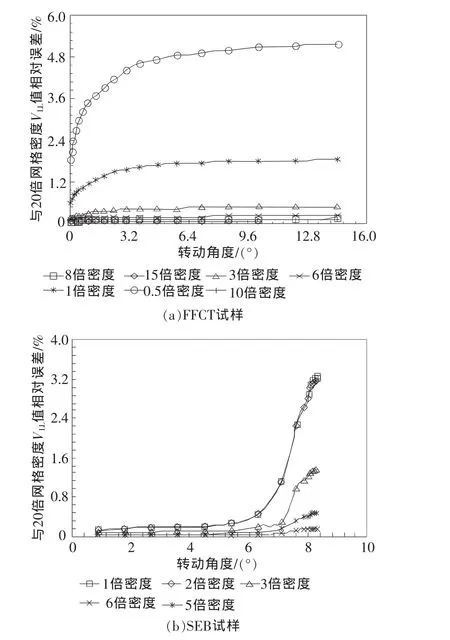
圖3 不同裂尖網格密度加載線張開位移VLL與20倍網格密度結果之間的相對誤差

圖4 有限元計算模型

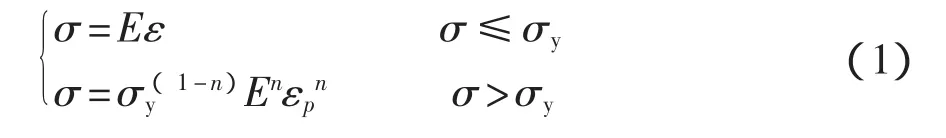
式中：E——彈性模量；

σy——名義屈服應力；

n——材料應變硬化指數。

假設模型滿足塑性增量理論，除了上述3個參量，描述材料彈塑性本構關系的參量還包括泊松比ν。考慮塑性不可壓縮，塑性階段泊松比為0.5。基于有限元分析結果，彈性泊松比對VLL-V0結果影響甚微，故取彈性泊松比為0.3。為了探究裂紋長度及材料本構與COD轉換公式之間的關系，選取不同裂紋長度與寬度比a/W（0.5～0.75）、屈服應力σy（100～800MPa）、應變硬化指數 n（0.05～0.3）進行精細網格計算。

2.1 FFCT 試樣

文獻[6]中給出了裂尖小范圍屈服時FFCT試樣VLL-V0轉換公式，如式（2）所示。

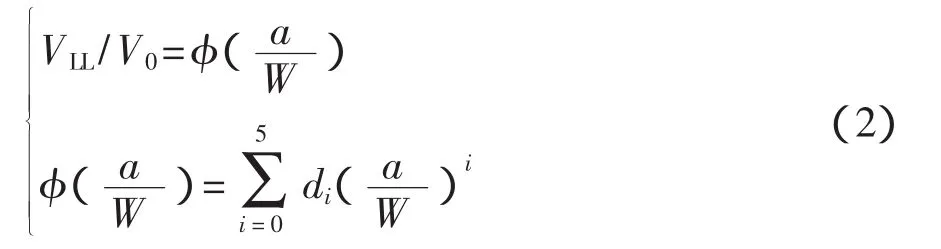
式中：a——裂紋長度；

W——試樣寬度；

系數di——分別為d0=0.225 5，d1=1.835 2，d2=-2.8064，d3=1.8742，d4=0.3276，d5=-0.6812。

文獻[8]中推導了FFCT試樣裂紋面發生較大轉動時的轉換公式：

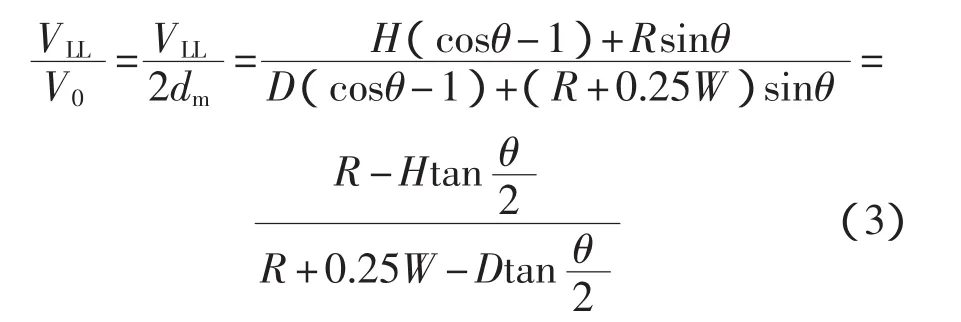
式中：H——加載孔中心到裂紋面的距離；

θ——FFCT試樣裂紋面繞轉動中心轉角的一半；

D——裂紋嘴COD引伸計標距的一半；

R——轉動半徑。

不受材料本構的影響，計算公式為

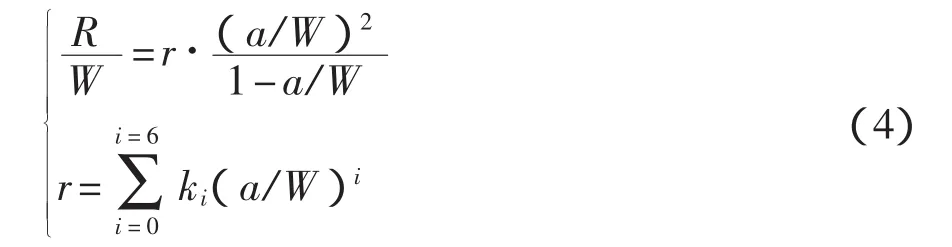
其中：k0=150.155 4，k1=-1 427.620，k2=5 712.630，k3=-12131.87，k4=14357.50，k5=-8967.939，k6=2309.530。

圖5為不同裂紋長度、不同本構關系所得有限元結果與由上述3種轉換公式計算所得結果。分析圖中數據可得以下結論：

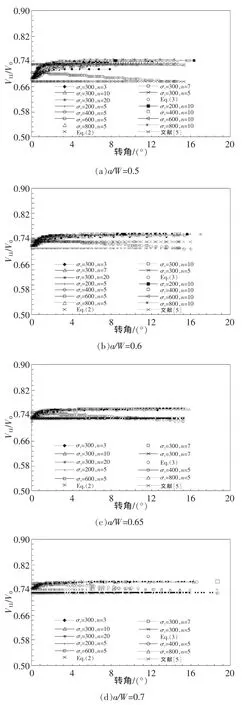
圖5 FFCT試樣不同裂紋長度a/W、不同材料對應的轉換比VLL/V0

（1）當轉動角度θ接近零度時，轉換比VLL/V0基本相同，即與材料性能無關；隨著角度增大，轉換比會出現一段非線性增長，當角度≥3°后，該比值趨于平穩，即轉動角度θ約為零度時，轉動中心位于某一點上，隨著載荷的增加，裂尖形成塑性鉸，轉動中心會產生少許移位；當轉動角度≥3°時，轉動中心趨于穩定，此時剛性轉動假設成立。

（2）固定a/W，轉動比會隨著硬化指數n或屈服強度σy的變化而變化，但每種工況下均落在一個很窄的帶寬內。由此可見，材料性能對轉換比的影響是有限的。

（3）當a/W增大時，分散帶帶寬逐漸減小，由此可見，材料的影響隨著a/W的增大逐漸減弱。

（4）式（2）和式（3）與精細網格化 FEA 結果之間均存在較大誤差，因此需要提出新的COD轉換公式，使其比值落于帶寬內，從而提高計算精度。

2.2 SEB試樣

金蕾、蔡力勛等[7]提出了裂尖小范圍屈服時SEB試樣VLL-V0轉換公式：

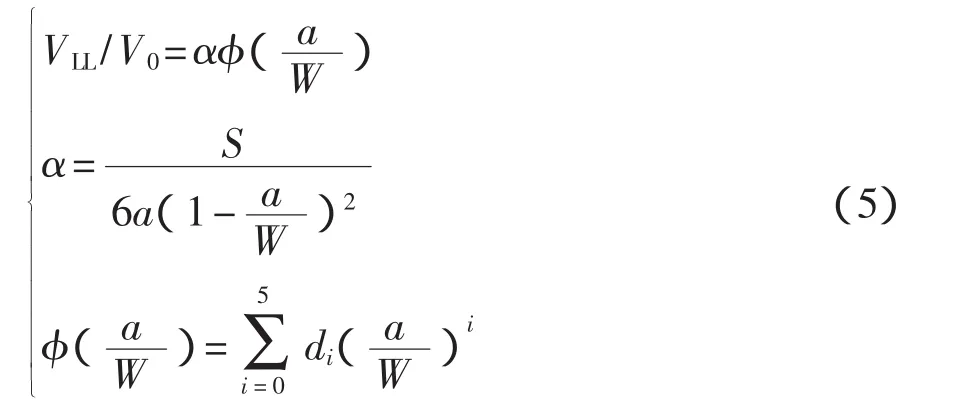
式中：S——SEB試樣的跨距；

系數di——分別為d0=0.831 70，d1=-0.649 80，d2=-2.1915，d3=3.7311，d4=-2.4600，d5=0.73900。

石凱凱、蔡力勛等[9]由SEB試樣幾何關系（見圖6），推導得到了考慮轉動效應的彈塑性轉換公式：

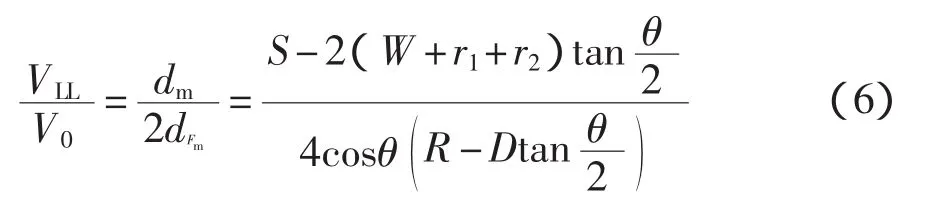
式中：r1、r2——支撐輥和加載輥的半徑。

R——轉動半徑，由式（4）計算得到，其中系數ki分別為：k0=13.4451，k1=-51.77885，k2=63.90878，k3=26.24999，k4=-145.89489，k5=137.81881，k6=-43.8174。

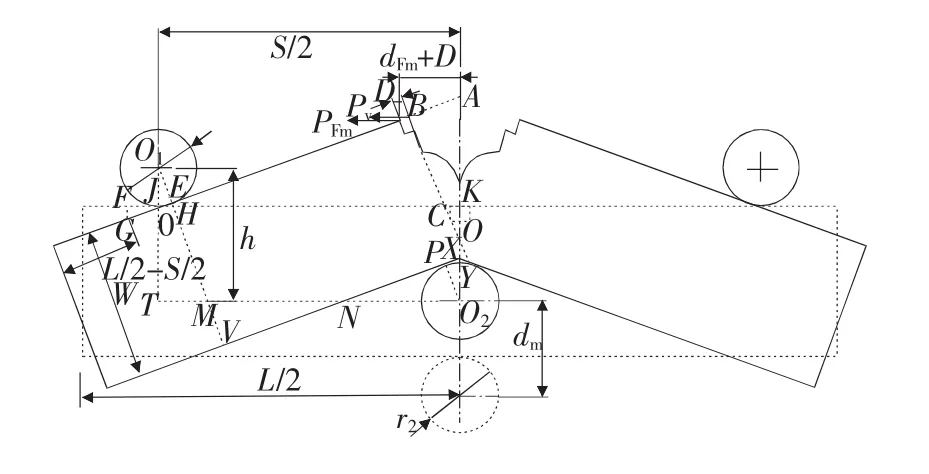
圖6 SEB試樣轉動圖解

圖7為SEB試樣有限元計算結果與由式（5）和式（6）計算所得結果對比圖。可得出與2.1節中的結論基本相似。

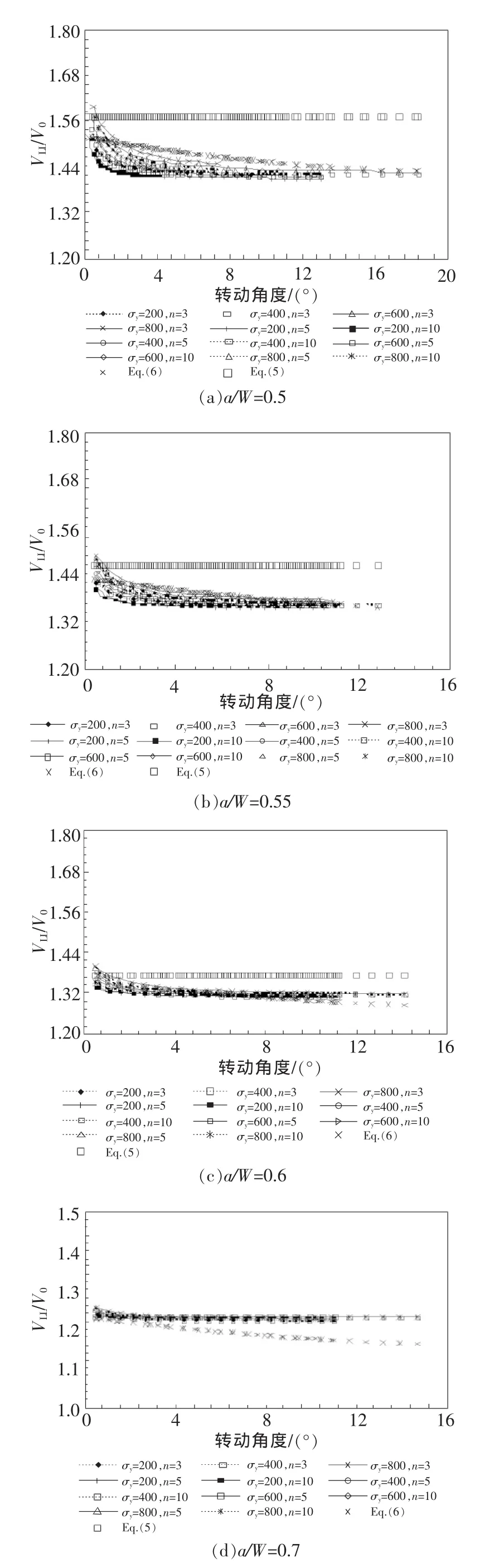
圖7 不同裂紋長度a/W、不同材料對應的轉換比VLL/V0

3 COD轉換公式

3.1 FFCT試樣

由2.1節結果分析可知，當裂紋面轉動角度θ較小時，VLL-V0轉換公式與材料屬性相關，其中所需考慮的參數包括裂紋長度a、屈服應力σy、材料應變硬化指數n等；因此，要得到由所有參數耦合的精確函數關系較為困難。依據圖8中幾何關系，提出如下VLL-V0轉換公式：

式中：R——裂紋面繞某一旋轉中心的轉動半徑，由上述式（4）進行計算。

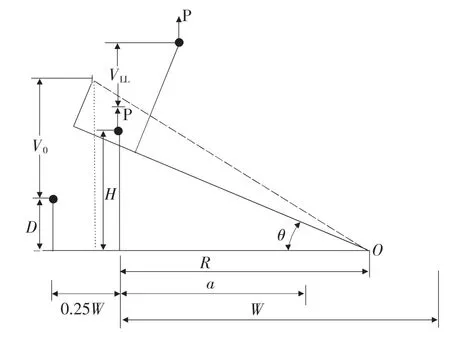
圖8 FFCT試樣轉動圖解

該式忽略了材料性能參數及FFCT試樣裂紋面轉動角度θ的影響，形式十分簡單。

圖9給出了不同材料、不同a/W情況下，ASTM E1921-2011推薦公式、式（2）、式（3）以及本文新式（7）與FEA結果之間的相對誤差，表1給出了公式結果與有限元結果之間的最大相對誤差。由此可見，當a/W>0.55時，本文提出的COD轉換公式的誤差均在3%以內，1%誤差時的置信度較高，比現有公式精度有了很大改善，形式簡單，計算方便。

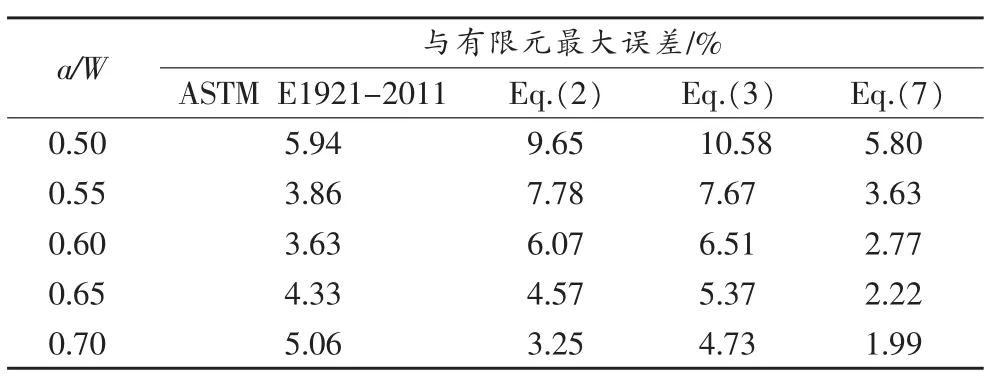
表1 FFCT試樣COD轉換公式與FEA結果相對誤差最大值

3.2 SEB試樣

與FFCT試樣相同，想要擬合出精確轉換公式較為困難，故通過有限元仿真計算，可得SEB試樣施力線位移VLL與裂紋嘴位移V0之間的關系：

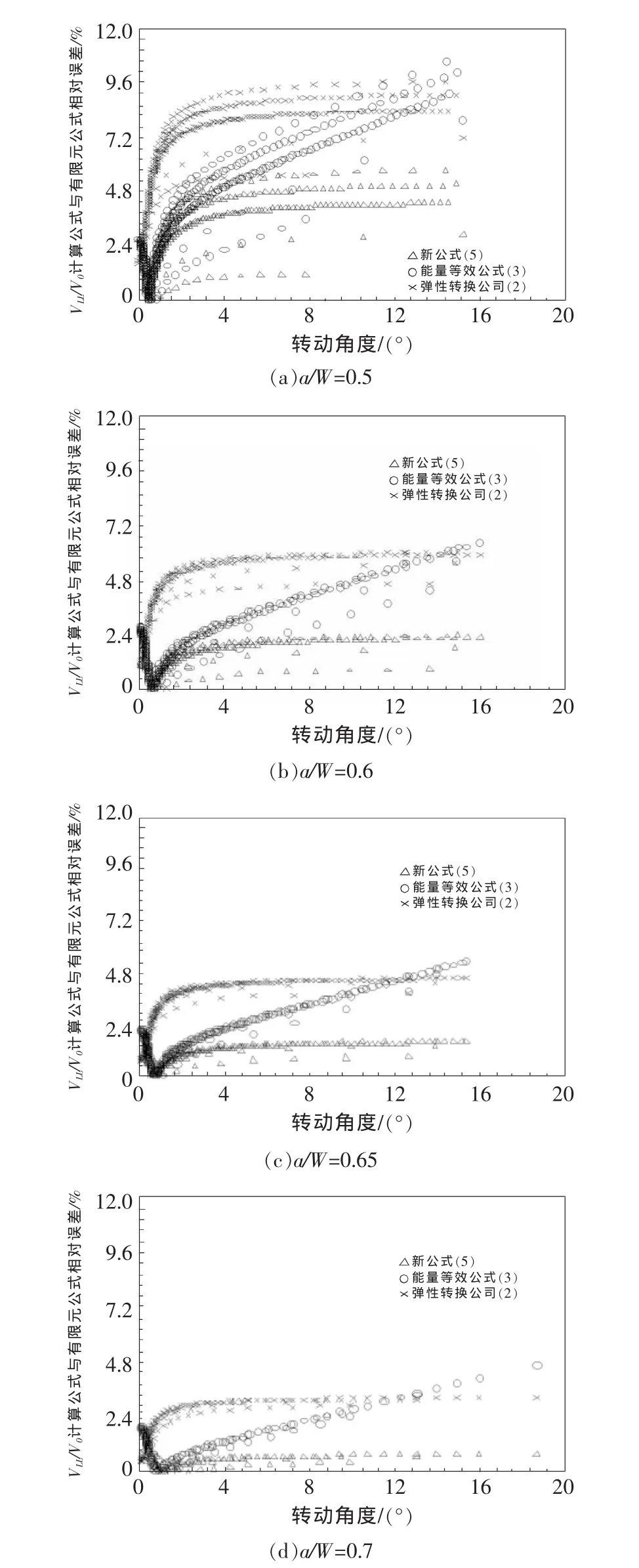
圖9 FFCT試樣不同a/W下VLL/V0與FEA結果相對誤差

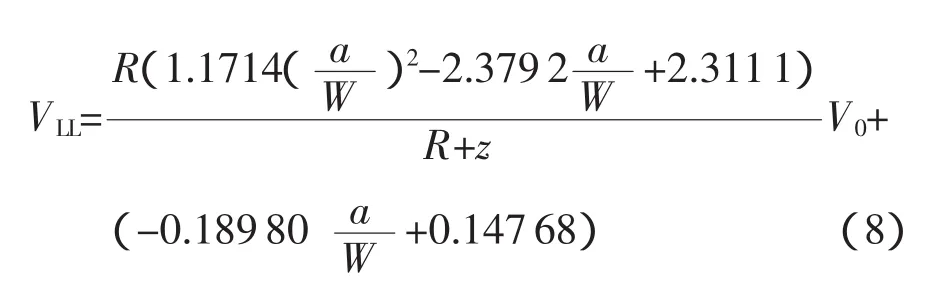
式中：R——試樣裂紋面繞轉動中心轉動的半徑，由式（4）進行計算；

z——用于測定缺口張開位移的引伸計裝卡位

置距離試樣表面之間的距離，即粘貼刀口厚度。

實驗中只要測得了裂紋嘴張開位移，帶入式（8）便可得施力線張開位移，用以計算J積分。

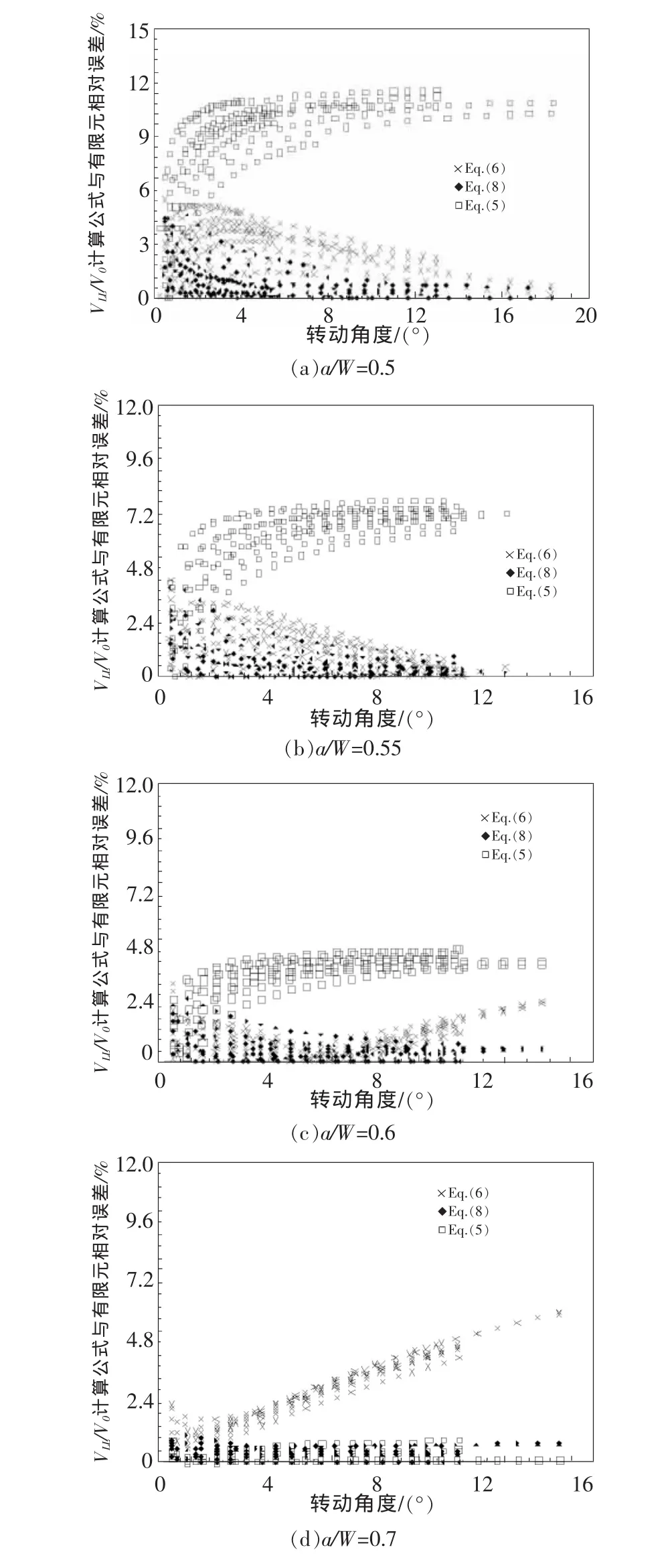
圖10 SEB試樣不同a/W下VLL/V0與FEA結果相對誤差

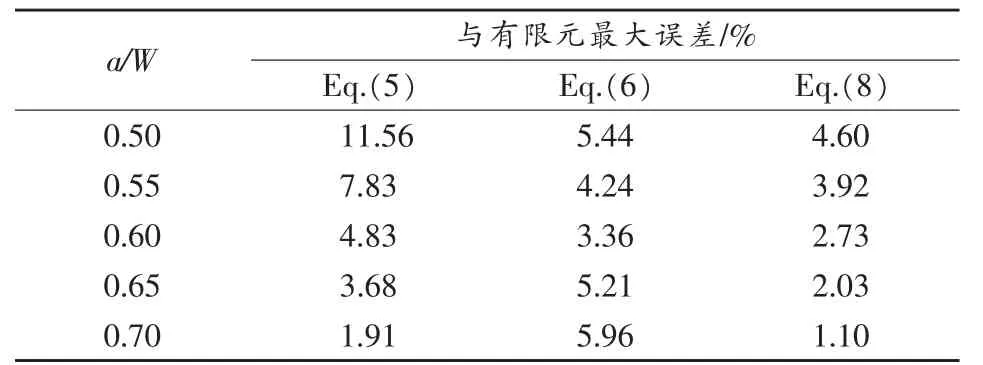
表2 SEB試樣COD轉換公式與FEA結果相對誤差最大值

圖10給出了多種不同材料、4種不同a/W情況下，式（5）、式（6）以及本文新式（8）與 FEA 結果之間的相對誤差，表2給出了公式結果與有限元結果之間的最大相對誤差。由此可見，當a/W>0.55時，本文提出的COD轉換公式的誤差均在3%以內，比現有公式精度有了很大改善，能夠更好地用于斷裂韌性測試中。

4 結束語

（1）通過對FFCT及SEB試樣裂尖不同網格密度進行有限元分析，提出了獲得穩定結果的計算模型，為得到VLL-V0轉換公式奠定基礎。

（2）基于有限元分析，對現有兩種試樣的轉換公式進行了誤差分析，并提出了分別針對FFCT及SEB試樣形式簡單且計算精度較高的COD轉換公式。

[1]Rice J R，Bosengren G F.Plane strain deformation near a crack tip in a power-law hardening material[J].Journal of the Mechanics and Physics of Solids，1968，16（1）：1-12.

[2]GB/T 21143—2007金屬材料準靜態斷裂韌度的統一試驗方法[S].北京：中國標準出版社，2008.

[3]ISO 12135—2002（E） International standard of unified method of test for the determination of quasistatic fracture toughness[S].International Organization for Standardization，Switzerland，2002.

[4]ASTM E1820-08a Standard test methods for measurement of fracture toughness:Annual Book of ASTM Standards[S].Philadelphia，PA：American Society for Testing and Materials，2008.

[5]ASTM E1921—2011 Standard test method for determination of reference temperature，To， for ferritic steels in the transition range[S].American Society for Testing and Materials，2011.

[6]蔡力勛，包陳，金蕾.金屬材料斷裂力學柔度測試技術問題與發展[J].中國測試，2009，35（1）：9-18.

[7]金蕾，蔡力勛.基于材料斷裂韌度測試的COD換算方法研究[J].機械強度，2010，32（1）：116-120.

[8]包陳，蔡力勛，石凱凱.直通型CT試樣COD彈塑性換算研究[J].北京科技大學學報，2011，33（7）：863-867.

[9]石凱凱，蔡力勛，包陳.單邊裂紋彎曲試樣的轉動修正方法研究[J].機械強度，2012，34（2）：250-255.