基于全相FFT的多頻比相測距方法研究

江曉東，謝京穩

(北京跟蹤與通信技術研究所， 北京100094)

0 引言

連續波比相測距雷達通過測量不同頻率信號之間的相位差來對目標距離進行測量，此種雷達具有結構簡單、測距精度高、便于采用數字信號處理技術等優點［1］。連續波比相測距雷達一般采用快速傅里葉變換(FFT)求解相位差。然而，傳統的FFT存在比較嚴重的頻譜泄露效應，頻譜泄漏會降低相位測量精度［2-3］。尤其是在多目標的情況下，信號的頻譜泄露會對其他信號頻譜的相位產生嚴重影響，降低相位估計精度，進而降低目標的測距精度。文獻［4］提出一種全相位FFT譜分析方法，并指出全相FFT比傳統FFT具有更優良的抑制頻譜泄漏性能。本文用全相FFT代替傳統的FFT來進行測量相位，并通過仿真驗證了全相FFT可有效得抑制頻譜泄露，從而提高此種雷達的測距精度。

1 比相測距原理

連續波比相測距的基本原理是雙頻比相測距，其原理如圖1所示。

假設發射兩個頻率為f0、f1，頻差為Δf的連續正弦波(f1=f0+Δf)。發射信號為S0(t)=cos(2πf0t+φ0)和S1(t)=cos(2πf1t+ φ1)，其中φ0和φ1為任意(常量)初相。回波信號由于多普勒效應產生頻移。接收機將兩個回波信號成分區分開來，并分別將各成分與相應的發射波形混頻，取出兩個多普勒頻率成分x0(t)、x1(t)。發射的兩個信號由于頻率差產生了一個與目標距離有關的相位差。

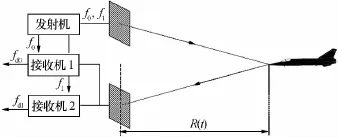
圖1 比相測距基本原理

FFT比相測距的一般流程如圖2所示，首先對x0(t)、x1(t)進行采樣，獲取 x0(n)、x1(n)，再對其分別作FFT，接著進行譜峰搜索，獲取譜峰譜線的位置序號k0、k1，再根據各自譜峰的實虛部求出相位φ0(k0)、φ1(k1)，以此作為各自對應信號的相位，然后求出兩者的相位差Δφ，再根據此相位差與距離的關系式就可確定對應的目標距離R。

雙頻比相測距系統由于存在最大不模糊距離和測距精度的矛盾［5］，現實中一般采用多頻測距來克服這一矛盾，常用的方法有“參差多頻”“二次差頻”等。本文采用“參差多頻”法，其具體內容及解模糊方法見文獻［5-6］。

圖2 比相測距算法基本流程

2 全相FFT譜分析方法簡述

全相位頻譜分析詳見文獻［7］，其大致過程如圖3所示。

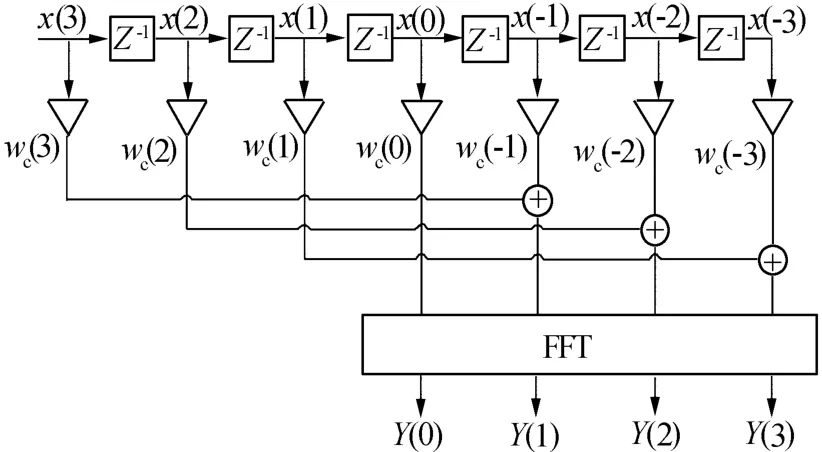
圖3 全相位FFT譜分析的基本框圖(N=4)

傳統FFT譜分析直接對采樣數據截斷后進行FFT即得譜分析結果，但一般情況下會導致較嚴重的頻譜泄漏效應。而全相FFT譜分析如圖3所示，即需用長為(2N-1)的卷積窗ωc對中心樣點x(0)前后(2N-1)個數據進行加權，然后將間隔為N的數據兩兩進行重疊相加，再對重疊相加后的N個數據進行FFT即得全相位譜分析結果。

圖3中的卷積窗由前窗f與翻轉的后窗b卷積而成［4］，即

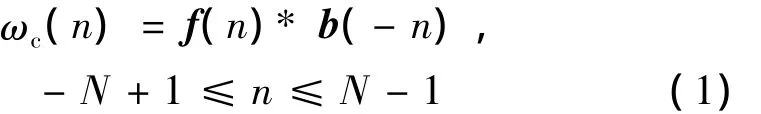
當 f，b 為對稱窗時，ωc(n)滿足

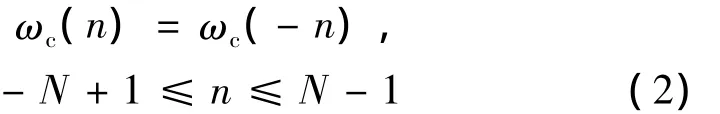
若f=b=RN(RN為矩形窗)，則稱為無窗全相位頻譜分析;若f，b中其一為RN，則稱單窗全相位頻譜分析;若f=b≠RN則稱為雙窗全相位頻譜分析。這里只討論無窗的情況。

全相FFT譜分析方法如下:首先用長為(2N-1)的卷積窗ωc對中心樣點x(0)前后(2N-1)個數據進行加權，然后將間隔為N的數據兩兩進行重疊相加，再對重疊相加后的N個數據進行FFT即得全相位譜分析結果。由可見FFT和全相FFT之間惟一的差別是對截斷數據預處理的方式不同［8］。

文獻［7］證明了全相FFT的兩個重要性質:

1)長度為(2N-1)的復指數序列經過N階無窗全相位FFT譜分析后，其主譜線上的相位譜值等于輸入序列的中心樣點相位的理論值，與信號的頻率偏差值無關。即全相位FFT譜分析具有“相位不變性質”。

2)序列{x(n)=ej(ω0n+θ0)，-N+1≤n≤N-1}歸一化后的全相位FFT振幅譜與傳統FFT振幅譜存在平方關系。

性質2是全相FFT譜分析的一個重要性質，它所揭示的平方關系是對所有N條譜線而言的，這就使得旁譜線相對于主譜線幅度的比例也按平方關系而減小，從而使主譜更為突出，繼而獲得很好的抑制頻譜泄漏性能。

3 基于全相FFT法的比相測距系統

本文提出利用全相FFT代替傳統FFT，這就構成基于全相FFT的比相測距系統，其一般計算流程如圖4所示。

圖4 基于全相FFT的比相測距算法流程

全相FFT的輸入數據為2N-1個數據{x(n)=ej(ω0n+θ0)，0≤n≤(2N-1)}其相位差與距離的轉換公式如下

式中:Δf=f1-f0;Δφ為兩個多普勒信號譜峰的相位差。

由式(3)可知:在目標作徑向勻速直線運動的情況下，經全相FFT處理所得的兩個多普勒信號譜峰相位之差Δφ按式(3)計算所得的距離表示的是t0+(N-1)Δt時刻的目標距離，即所對應采樣時間段中間時刻點的距離。

需要說明的是，式(3)是在目標作徑向勻速直線運動的條件下推導出來的，文獻［9-10］則給出了目標一般運動時的距離與相差的理論表達式，證明了目標在作一般運動時，其多普勒頻率不再是作徑向勻速直線運動時的常數，而是時變函數。然而這一公式需要首先求出目標的瞬時速度和加速度，這兩個量往往本身就是未知的，所以這一公式還無法直接運用到工程實踐中。但是，目標在作一般運動時，只要其徑向加速度不大，在很短的采樣間里，其多普勒頻率變化不大，仍然可以利用式(3)求解目標距離。

4 仿真結果

為驗證全相FFT在多目標下抑制頻譜泄露的性能，對多目標作徑向勻速直線運動情況進行計算機仿真。

1)仿真條件:

目標參數:設雷達波束范圍內共有4個目標，其速度分別為 100 m/s ，230 m/s，260 m/s，400 m/s(遠離雷達為負，否則為正);目標初始距離均為10 km;雷達回波幅度均為常數1，不隨目標距離改變。

雷達參數:雷達基準頻率f0=10.5 GHz，基本頻差5.4 MHz，參差重數取3，參差系數為(7，8，9)。采樣頻率125 kHz。FFT點數為1 024，每隔1 024個采樣點計算1次距離，共計算1 000點。

2)仿真結果:

(1)波束范圍內單目標

設在測量時段，速度為100 m/s，230 m/s，260 m/s，400 m/s的四個目標回波依次出現在雷達波束范圍內，互不影響，且回波信號沒有受到噪聲干擾，即信噪比為無窮大。雷達對單目標進行距離測量，則對4個目標的測距精度如圖5所示。

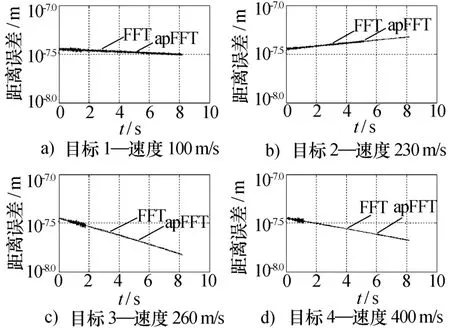
圖5 無噪單目標情況下的測距精度

由圖5可知，傳統FFT和全相FFT比相后解得的距離與理論上的理想距離(采樣時間段中間點所對應目標距離)之間絕對誤差均小于10-7m，所以在無噪聲且雷達波束內只有單目標的情況下，FFT和全相FFT均可準確得測得目標距離，這也證明了式(3)的正確性。

(2)波束范圍內多目標

設在測量時段，速度為100 m/s ，230 m/s，260 m/s，400 m/s的4個目標回波同時出現在雷達波束范圍內，且沒有受到噪聲干擾，即信噪比為無窮大。雷達對多個目標同時進行距離測量，則對4個目標的測距精度如對圖6所示。

將圖6與圖5對比可知，在無噪多目標的情況下，不論是采用傳統FFT，還是采用全相FFT，4個目標的測距精度都嚴重下降。這是由于各個信號的頻譜泄露互相影響，降低了相位測量精度，從而降低了測距精度。

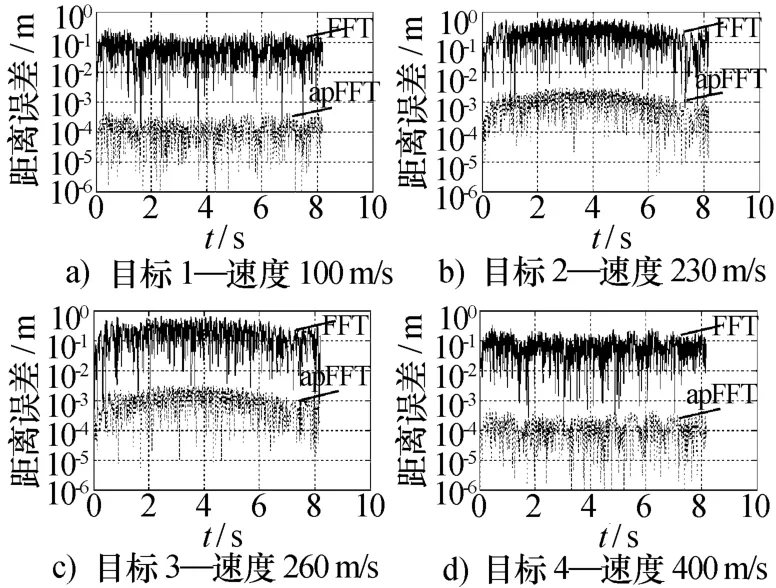
圖6 無噪多目標情況下的測距精度

對于FFT法來說，4個目標的測距精度均由約10-7m降低到10-1m，整整降低了6個數量級，由此可見在無噪多目標的情況下，當采用FFT比相測距時，頻譜泄露對相位測量的影響是十分嚴重的。這極大地降低了此種雷達的多目標情況下的測距精度，故必須采用一些抑制頻譜泄露的方法。

對于全相FFT來說，由于具有較好的頻譜泄露能力，相比于傳統FFT，頻譜泄露造成影響較弱。對于目標1和4來說，由于速度與其他目標速度相差較遠，故多普勒頻率相差較遠，所以受到其他多普勒信號頻譜泄露的影響較輕，故其測距精度相對于無噪單目標情況下測距精度只降低了約4個數量級，優于10-3m，遠遠高于傳統FFT在此種情況下10-1m的測距精度;而對于目標2和目標3來說，由于彼此的頻率間隔較近，頻譜泄露較為嚴重，其測距精度相對于無噪單目標情況下測距精度約降低了5個數量級，但依然優于10-2m，仍高于傳統FFT在此種情況下10-1m的測距精度。

(3)波束范圍內多目標，信噪比為40 dB，蒙特卡洛仿真200次

設在測量時段，速度為100 m/s ，230 m/s，260 m/s，400 m/s的4個目標回波一同出現在雷達波束范圍內，同時回波受到噪聲干擾，信噪比為40 dB。雷達對多個目標同時進行距離測量，則對4個目標的測距精度如圖7所示。

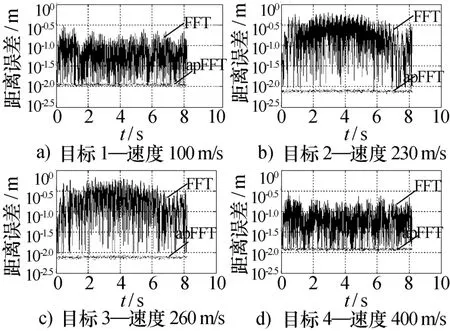
圖7 有噪多目標情況下的測距精度

對比圖6與圖7可知，在有噪聲的情況下，由于回波信號受到噪聲干擾，不論是采用FFT，還是采用全相FFT，測距精度均下降，但是全相FFT的測距精度，仍然要比FFT高出一個數量級，可見即使是在有噪多目標的情況下，全相FFT也要比FFT有著更高的測距精度。

綜上可知，若雷達波束內同時出現多目標，由于不可避免的頻譜泄露，會極大地降低多頻比相測距雷達的測距精度。在此種情況下，全相FFT相比于傳統FFT，能夠較好的抑制了頻譜泄露，從而極大地提高了多頻比相測距雷達在多目標情況下的測距精度。

5 結束語

在多頻連續波比相測距雷達中，本文利用全相FFT代替了傳統FFT，通過計算機仿真，證明了全相FFT比傳統FFT有著更好得抑制頻譜泄露的能力，提高了各頻率分量的測相精度，進而有效提高了多頻比相測距雷達在多目標情況下測距精度。

［1］許邦建，王 展，皇甫堪.FFT比相測距雷達中的相差—距離關系研究［J］.兵工學報，2001，22(1):53-56.Xu Bangjian，Wang Zhan，Huang Fukan.Relationship between phase difference and range in FFT phase-comparing ranging radars［J］.Acta Armamentarii，2001，22(1):53-56.

［2］Xie Ming，Ding Kang.Correction for the frequency amplitude and phase in FFT of harmonic signal［J］.Mechanical System and Signal Processing，1996，10(2):211-221.

［3］Dusan Agrez.Improving phase estimation with leakage minimization［J］.IEEE Transactions on Instrumentation and Measurement，2005，54(4):1347-1353.

［4］王兆華，黃翔東.數字信號全相位譜分析與濾波技術［M］.北京:電子工業出版社，2009.Wang Zhaohua，Huang Xiangdong.Digital signal all-phase spectrum analysis and filtering technology［M］.Beijing:Publishing House of Electronics Industry，2009.

［5］曹延偉.多頻連續波雷達跟蹤控制器設計及相關理論和算法研究［D］.長沙:國防科技大學，2005.Cao Yanwei.Design of tracking controller of multiple frequency CW radar and research on related theory and algorithm［D］.Changsha:National University of Defense Technology，2005.

［6］許邦建，李 綱，皇甫堪.測距雷達解距離模糊的兩種快速算法［J］.電子與信息學報，2001，23(9):905-911.Xu Bangjian，Li Gang，Huang Fukan.Two fast algorithms of deambiguous technique in ranging radar［J］.Journal of Electronics and Information Technology，2001，23(9):905-911.

［7］黃翔東.全相位數字信號處理［D］.天津:天津大學，2006.Hua Xiangdong.All-phase digital signal processing［D］.Tianjin:Tianjin University，2006.

［8］王兆華，黃翔東.基于全相位譜分析的相位測量原理及其應用［J］.數據采集與處理，2009，24(6):777-782.Wang Zhaohua，Huang Xiangdong.Principle of phase measurement and its application based on all-phase spectral analysis［J］.Journal of Data Acquisition and Processing，2009，24(6):777-782.

［9］袁俊泉.皇甫堪.機動目標情況下FFT比相測距方法研究［J］.現代雷達，2005，27(9):14-17.Yuan Junquan，Huang Fukan.A study on ranging method based on FFT phase comparison for maneuvering target［J］.Modern Radar，2005，27(9):14-17.

［10］Yasotharan A，Thayaparan T.The performance of the fourier method in detecting an accelerating target and estimating its median velocity［C］//IEEE International Radar Conference(Section II).［S.l.］:IEEE Press，2000:59-64.