“中國 美國 新加坡”小學數學教材中的“分數定義”

蒲淑萍

（1.重慶師范大學 初等教育學院，重慶 401331；2.華東師范大學，上海 200241）

1 研究背景

大量研究表明，分數教學有諸多的障礙與困惑[1～2].原因在于分數是兒童第一次學習數學中有關兩個量的相對比較關系，且分數具有多重意義（如部分/全體、集合、數線意義、商、比例等）、多重子概念（如單位概念、等分概念等），而這些子概念又牽涉“連續量”與“離散量”的不同情境，并具有一些特殊的性質，如：等值、稠密性等[3]，因此學生在學習分數概念時需要經歷漫長且艱苦的發展過程[4].Kieren提出：教師有必要掌握分數的各種意義，并以各種意義為基礎設計分數問題，將有助于發展并考量學生對分數概念的認知[5].

當前在各種國際數學成績測試中，如TIMSS，PISA，IEA等，中國、新加坡的學生成績位居前列，而美國的數學學業成績則一直處于后面幾位.然而進一步的調查也發現，位居前列的新加坡、中國的學生對于數學學習的自信心、興趣等的調查結果卻大相徑庭，而美國學生成績雖不盡如人意，但學生對數學的信心、興趣以及創造力等方面卻明顯優于中國[6].通過與別國對比，分析比對各自的優勢與不足，相互借鑒，尋找東西方數學教育優勢互補的中間地帶已成為主流趨勢.探究、分析新加坡、美國的數學教育，可為中國的數學教育提供參照、借鑒.

教材是影響學生學業成就的關鍵要素之一.那么對于“分數”這一被各國視為難點的教學內容，中、美、新加坡三國教材是怎樣處理的呢？怎樣的呈現方式與教學順序更符合學生的認知？對此，以3個國家教材中的“分數定義”為突破口進行對比研究，他山之石可以攻玉，希望能為中國小學數學教材編寫與課堂教學提供借鑒.

2 教材選取與研究問題

學生對分數內容的學習困難，在很大程度上可歸結為對分數意義或定義的不明所造成的.研究擬從教科書層面出發，以中國、新加坡、美國的小學數學主流教材：中國的人教版[7～9]，新加坡的Discover Maths[10～14]，以及美國加州小學數學教材California Mathematics[15]三套教材，選取各自教材中“分數定義”內容進行詳細的案例研究.中國、新加坡、美國3國的小學均為6年制，中國和新加坡的教材都是每個年級兩冊，共12冊；美國加州則是每個學年一冊，共6冊教科書.3個國家小學數學教材中都有分數內容，且都是采取螺旋上升的方式設置.因此就分數定義而言，3個國家的教材具有可比性.

對于教材中的分數定義主要關注兩個方面：

（1）各國教材中出現了哪幾種分數定義？它們的呈現順序是怎樣的？

（2）幾種定義采用了怎樣的表征形式？定義之間的聯系是怎樣的？

3 研究方法

研究主要采用“內容比較、分析法（Content analysis）”，這種方法是研究教科書常見的方法之一.因三地教材所用紙張大小、使用文字的差異等，僅從內容所占頁碼的多少等表層“量”的比對并不能反映三地教材的本質差異.故而，本研究主要采用定性分析的方法，對內容進行深入地、多維度地比對、分析，以此為基礎進行解釋與推論.比較分析的內容主要包括：（1）各國教材中出現的定義種類及呈現順序；（2）各類定義的表征形式及各種定義之間的聯系.

4 結果及分析

4.1 各類定義及呈現順序對比

4.1.1 分數定義

關于分數定義，張奠宙、呂玉琴、Kieran等都進行過研究，通常認為分數定義建立在以下4種意義的基礎之上，各種意義最后均連接至分數最核心的“除的意義”.①平分的意義：從平分入手學習分數，是一條比較容易的途徑，也比較容易化解分數學習中常見的認知沖突；②測量的意義：為解決測量時不足一個單位度量長度時的問題，通常就會引出分數或小數；因為強調單位，故而，測量是調和“部分/全體”的意義與帶分數認知沖突中的重要工具；③比例的意義：比的原理，是一種微妙的平分方式，因此學生比較容易接受.比值的引入，讓分數具有解決比例問題的意義；④部分/全體的意義：是分數的重要意義之一，但是由于概念較為抽象，而且真分數的暗示過深（整體為1），可能造成假分數或帶分數學習上的困擾，必須透過單位的強調來解決其認知沖突.

盡管學者們對分數所下定義不同，但大致可歸納出，出現在小學教材中的分數定義大致有如下4種，分別為：份數定義—部分/整體（包含子集/集合）關系、數線定義（數線上一點）、商的定義（整數相除）、比/比值（部分/部分）.而且在設置順序上，他們均認為分數的定義在不同的學齡階段有著不同的內涵，也就是，隨著人們對分數認識的不斷深入，分數定義的內涵不斷拓展，逐漸抽象化.

3個國家小學數學教材中分數定義是怎樣呈現的呢？

4.1.2 三個國家小學教材中的分數定義

3個國家教材均對分數的多重意義有所體現，但各種定義呈現時間及順序有所不同，各類定義之間聯系亦不相同，具體見表1.

表1 “中國 美國 新加坡”小學數學教材分數定義的比較

4.1.3 對結果的分析

相同之處：

（1）4種“定義”都在三國教材中出現；

（2）都以“份數定義”為主；

（3）都是呈螺旋上升的方式；

（4）在份數定義中，都是按照從平分開始，介紹單位分數，再到一般分數，真分數、假分數的順序；

（5）三國教材對除“份數定義”以外的各類定義均采取了“模糊”處理，沒有明確說法，只有一些描述性語言，如分數“商的定義”，在3個國家教材中，都沒有出現“分數是整數q除以整數p（p≠0）所得的商”這樣明確的說法，而只有“比較分數與除法”發現兩者之間關系或“作為商的分數”的提法.

不同之處：

（1）“份數定義”不同的處理方式：分數的“份數定義”在三國教材中，都是分數定義的主要呈現方式，但是相比而言，也有著明顯的不同：

①出現時間的不同：美國加州教材的“份數定義”出現最早，在二年級前半段（相當于中國、新加坡分冊處理的上冊）；新加坡教材次之，出現在二年級下冊；中國最晚，在三年級上冊出現；

②螺旋的次數不盡相同：從表1中可以看到，完整地介紹“份數定義”，中國只用兩次（三上與五下），而新加坡和美國教材則經歷3次螺旋上升，才完整呈現；

③在“份數定義”中，最大的不同就是新加坡、美國教材中均是按照“parts of a whole”→“parts of a group”→“parts of a set”的順序，從3個不同層次逐步給出各類情境下的“部分/整體”的分數定義，而中國教材只有一種提法，就是“整體中的部分”，在相應練習中出現如圖1所示問題，使學生通過解決此類問題或多或少感受并理解“集合”意義上的“份數定義”.

圖1 中國教材中的處理方式

（2）“除法定義”不同的處理方式：3個國家教材最大的不同體現在對除法與分數關系以及化假分數為帶分數的問題處理上.

①中國與美國的教材從平均分配的另外一種方法——除法，引出“作為商的分數”，而新加坡教材則仍從分數的“份數定義”出發引出除法算式與之對應的意義解釋；

②在處理利用除法化假分數為帶分數的問題上，三國教材雖都是通過具體例題展示：商的整數部分作為帶分數的整數部分，余數對應分子，所不同的是，新加坡與美國以明確的方式，采用豎式給出做法及除法豎式與分數各個構成成分之間的對應關系；而中國教材先通過問題“一個半”該如何表示，引出帶分數定義，后出示例子展示化假分數為整數（整除的情形）或帶分數的做法，通過先將分數化為橫式除法，再給出帶分數表示的做法.

（3）集中程度不同.

相比而言，中國的分數內容主要集中在三年級上冊和五年級下冊，而新加坡和美國教材則分散在從二年級開始，跨越二、三、四、五，甚至六年級（新加坡），相比中國的設置，顯得分散了許多.

（4）對“數線定義”處理方式不同.

張奠宙先生認為：“在過渡到分數的商定義時，在數直線上對分數作幾何解釋是非常重要的.”[16]事實上，中國教材卻是先出現了“商的定義”后才出現“數線上的表示”.誠如張先生所言：“我國的分數教學，擅長分數的計算，不大注意在數軸上直觀地加以表示.”相比而言，對數線定義最為重視的當屬加州教材，教材中先后多次用“數線”表示分數，內容涉及“例題”、“練習”、“活動”等欄目，并在五年級上學期教學內容中專門有一節“數線上的分數（Fractions on a Number Line）”作為數學實驗內容，引導學生進行探究.

圖2展示了新加坡教材中數線出現之前的幾何模型，圖3展示美國加州教材中“數線上的分數”的探究實驗內容.

圖2 新加坡教材二（下）中數線出現之前的幾何模型

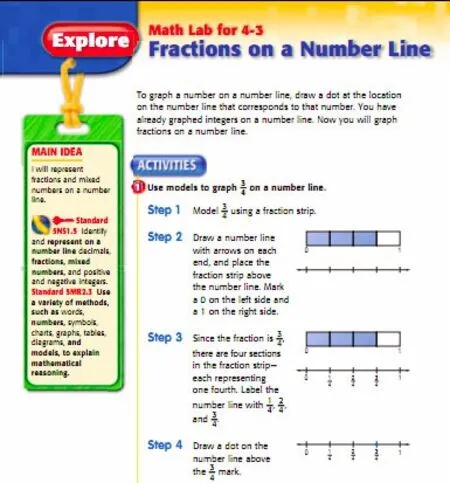
圖3 美國加州教材中“數線上的分數”的探究實驗內容

4.2 分數定義不同表征形式及其作用

“表征”是學習的重要媒介，也是個體思考與溝通的重要工具，與數學學習有密不可分的關系.表征的功能有：①使數學概念具體化；②可成為溝通的工具；③可成為思考的材料；④可成為解題的工具.Lesh，Post和Behr[17]提到數學學習與數學問題有5種不同的表征，包括現實情境（real-world situation）、操作模型（manipulative models）、圖（picture）、口語符號（spoken symbols）及書寫符號（written symbols）.在數學學習的過程中，不同的表征對兒童的概念理解產生重要影響，而且也直接影響著問題解決的難易.Behr，Wachsmuth，Post和Lesh[18]強調表征間的轉換能力是影響學生數學學習、問題解決及產生、有意義學習的重要因素.通常認為，多種表征形式有助于學生對抽象概念的理解.那么分數定義中的表征形式有哪些？各國在表征形式的選取上是否相同？值得探究.

分數的概念較整數更抽象，而實物和圖畫式等表征形式更易使學生掌握分數的符號規則.三國教材中，都采用了多種表征形式.這里以分數的“份數定義”這一主要定義形式為例進行比較，希望對中國教材處理抽象概念的表征形式提供一點參考.

可以看到，3個國家“份數定義”中大體都采用了如下4種表征形式：現實情境、具體操作物、圖形、符號（教材中主要是書寫符號）.因3個國家教材對“份數定義”處理的不同，單從數量并不能說明各自的差異，這里主要對“份數定義”中各類表征形式之間的聯系進行比對，發現3個國家教材對定義中表征形式的處理并不相同.

在表征順序上，中國教材多從具體情境出發，引出問題，借助具體操作物，進而過渡到“圖形”表征，在做了這些準備后，給出定義及符號表達.這種處理方式體現了“數學化”的過程及思想；加州教材多是從定義出發，介紹定義及符號表示，后借助具體操作物、圖形解決問題，多在后面練習及問題解決中出現與該內容相聯系的現實情境，似乎是為尋找知識在生活中的“作用”；新加坡教材則從“折紙”等具體操作入手，給出對應“符號”，再給出相應文字定義.種種做法孰優孰劣，很難直接下結論，在教學中可嘗試多種教學設計，探尋更加符合學生認知的表征形式的呈現過程.

5 啟 示

5.1 對分數定義處理的啟示

5.1.1 份數定義宜分層次處理

相比新加坡、美國教材對“份數定義”的處理，中國教材有較為明顯的不足.新加坡、美國教材利用不同情境給出“份數定義”：“整體中的部分”、“組合里面的部分”再到“集合中的部分”，分成3個不同層次，逐步增加概念的抽象程度.這樣做可使學生清晰感知分數“單位”的多種適當選擇，有利于學生完整地、深入地理解“份數定義”.而中國教材“整體中的部分”的單一提法，易造成學生認識上的不足或錯誤理解[19].因此建議：份數定義的處理宜借鑒新加坡、美國教材的做法，對中國教材做出改進.

5.1.2 改進分數“商的定義”教材處理

分數的真正來源，在于自然數除法的推廣.按照張奠宙先生的說法，分數“商的定義”體現了分數的本質，符合數系擴張的數學思想，理應成為分數引入、分數定義的首選的、核心的內容.三國教材盡管對“除法與分數”之間關系都用不少篇幅展開，但對其作用與意義突出不夠.試想，若從“商的定義”入手引入分數，再到分割形成的“份數定義”，再到數軸上任意大小的分數，會否有助于去除當今教學中存在的對分數的種種認識不足（比如認為分數比1小，分數基本性質中對相等分數的錯誤認識），這樣的順序是否更有利于學生對分數概念的理解與建構？這值得思考.

5.1.3 加強分數“數線定義”的內容及教學

將分數在數線上直觀表達出來，是促進學生正確理解分數定義的有力工具.它起到了將現實情境與具體操作物進一步轉化為“數學符號”的作用，是溝通各種表征形式的良好介質，教材及教學理應重視其作用，增加分數“數線定義”的內容.在此，新加坡教材給了我們良好的啟發：從“細長條形塊”這一幾何模型逐漸過渡到數學的語言與符號——數線，逐步抽象，更加符合學生的認知發展.

5.2 對教學實踐的啟示

長期以來中國教材及教學多采用“情境創設——提出問題——實物操作——‘圖形’表征——定義、符號”的基本順序，這種做法體現了數學與實際生活的聯系.然而，數學本身的學科特征使其某種程度上具有脫離情境的特征，比如其幾何解釋、符號表達等.同時“現實情境”、“具體操作物”、“圖形”等表征形式無一不為分數的“符號”表征及其認知服務.倘若一味強調上述順序則易使教學陷入某種僵化模式，不利于學生對數學抽象本質的把握.需要處理好“數學與日常生活的聯系”與“數學的形式特性”之間關系的辯證統一，既要突出知識的內在聯系，又不過分強調情境學習[20].因此，結合內容特點，適度采用多元化的表征順序，這方面新加坡教材、加州教材給予研究者重要啟示.如，對分數定義，就不妨就從數學化的“商的定義”入手，以此為核心，聯系分配、測量、比例等意義，逐步給出“份數定義”、“數線定義”及“比的定義”，則更有益于去除現今教學中學生易產生錯誤理解之處.為增強知識與實際生活的聯系，可在學生真正掌握分數本質后，給出與實際生活聯系密切的例子.再如，化假分數為帶分數內容的處理，可適當簡化，在分數除法定義的基礎上，直接給出具體做法，而無需做多余的鋪墊.總之，教學中宜視具體內容的不同而采取不同的表征順序和處理方式.同時，多種不同的教學處理方式對學生思維發展的多維度、多向性亦是有益的.這是三國教材分數定義比較給予研究者的重要啟示.

從教材比較的角度來看，文章僅對中、美、新三國教材對分數定義的處理進行了比對，對于分數內容，學生的學習困難不僅在定義，對分數的運算也存在很多問題，如對分數除法“顛倒相乘”的算理缺乏足夠認識等，美、新兩國是如何處理分數四則運算的？以及3套教材除卻分數外的其它內容是否有可資借鑒的地方？另外，對于教材比較應采用的方法、針對不同內容應選擇的合適切入點等都值得研究者深入、細致地分析、思考，以期通過合理、有效的方式比較、借鑒別國教材的成功做法，逐步改進中國的教材與教學.

[1]Paik J H.Fraction concepts: A Complex System of Mapping [D].Indiana University, ProQuest Information and Learning Company, 2005.

[2]鞏子坤，楊玉東.錯誤僅僅是因為粗心嗎[J].上海教育科研，2007，（9）：90-93.

[3]Kieren T E.On the Mathematical, Cognitive and Instructional Foundations of Rational Numbers [A].In: Lesh R A.Number and Measurement: Papers from a Research Workshop [C].Columbus, OH: ERIC/SMEAC, 1976.

[4]呂玉琴.分數概念文獻探討[J].臺北師院學報，1991，（4）：573-605.

[5]Kieren T E.Rational and Fractional Numbers: From Quotient Fields to Recursive Understanding [A].In: Carpenter T P,Fennema E, Romberg T A.Rational Numbers: An Integration of Research [C].Hillsdale, NJ: Lawrence Erlbaum, 1993.

[6]Ministry of Education, Singapore.Singapore Tops the Trends in International Mthematics and Science Study (Timss)2003 [EB/OL].http://www.moe.gov.sg/media/press/2004/pr20041214.htm.

[7]盧江，楊剛.義務教育課程標準實驗教科書小學數學三年級（上）[M].北京：人民教育出版社，2003.

[8]盧江，楊剛.義務教育課程標準實驗教科書小學數學五年級（下）[M].北京：人民教育出版社，2005.

[9]盧江，楊剛.義務教育課程標準實驗教科書小學數學六年級（下）[M].北京：人民教育出版社，2006.

[10]Teo S, Tiang K M.Discover Maths Textbook 2B [M].Singapore: Panpac Education Private Limited, 2007.

[11]Teo S, Tiang K M.Discover Maths Textbook 3B [M].Singapore: Panpac Education Private Limited, 2007.

[12]Shing L H.Discover Maths Textbook 4A [M].Singapore: Panpac Education Private Limited, 2007.

[13]Lai C C, Tan K L.Discover Maths Textbook 5A [M].Singapore: Panpac Education Private Limited, 2007.

[14]Lai C C, Tan K L.Discover Maths Textbook 6A [M].Singapore: Panpac Education Private Limited, 2009.

[15]Altieri M B.California Maths (Grade 2, 3, 4, 5) [M].Macmillan: McGraw-Hill, 2007.

[16]張奠宙.分數的定義[J].小學教學（數學版），2010，（01）：48-49.

[17]Lesh R, Post T, Behr M.Representations and Translations among Representations in Mathematics Learning and Problem Solving [A].In: Janiver C.Problems of Representations in the Teaching and Learning of Mathematics [M].Hilladale,NJ: Lawrence Erlbaum, 1987.

[18]Behr M J, Wachsmuth I, Post T R, et al.Order and Equivalence of Rational Numbers: A Clinical Teaching Experiment[J].Journal for Research in Mathematics Education, 1984, (15): 323-341.

[19]張奠宙.“分數”教學中需要澄清的幾個數學問題[J].小學教學（數學版），2010，（1）：4-6.

[20]鄭毓信.數學教育哲學的理論與實踐[M].南寧：廣西教育出版社，2008.