導彈速度時變的攻擊時間與攻擊角度控制導引律

馬國欣, 張友安

(海軍航空工程學院 控制工程系, 山東 煙臺 264001)

2012-09-13;

2012-12-17; < class="emphasis_bold">網(wǎng)絡(luò)出版時間

時間:2013-04-09 09:58

國家自然科學基金資助(61273058)

馬國欣(1983-),男,河北趙縣人,博士研究生,研究方向為飛行器精確制導理論與控制;

張友安(1963-),男,湖北天門人,教授,博士生導師,研究方向為先進控制技術(shù)及其在飛行器中的應(yīng)用。

導彈速度時變的攻擊時間與攻擊角度控制導引律

馬國欣, 張友安

(海軍航空工程學院 控制工程系, 山東 煙臺 264001)

針對導彈速度非定常情況下的協(xié)同制導問題,提出了兩種分別滿足攻擊時間約束、攻擊時間與攻擊角度約束的導引律。首先通過求解導彈在比例導引(PN)及帶攻擊角度約束的偏置比例導引(BPNIAC)下的系統(tǒng)微分方程,得到導彈飛行的實際剩余航程,并根據(jù)指定的攻擊時間與導彈的實際速度曲線構(gòu)造標稱剩余航程,將攻擊時間控制問題轉(zhuǎn)化為導彈實際剩余航程對標稱剩余航程的跟蹤問題。然后,在PN及BPNIAC的基礎(chǔ)上附加反饋控制項使導彈實際的剩余航程跟蹤標稱值,從而實現(xiàn)導彈速度時變情況下攻擊時間的控制要求。仿真結(jié)果驗證了該方法的有效性,實際應(yīng)用中可根據(jù)預測速度曲線及在線更新策略對標稱剩余航程進行估算。

比例導引; 攻擊時間; 攻擊角度; 時變速度; 協(xié)同制導

0 引言

目前,帶有攻擊時間與攻擊角度約束的精確制導問題已受到越來越多研究者的關(guān)注。關(guān)于攻擊角度控制的文獻已有很多,從滿足攻擊角度要求的偏置比例導引律[1-2]到最優(yōu)控制導引律[3-6],從Lyapunov方法[7]到反演控制方法[8],不勝枚舉。而關(guān)于攻擊時間控制的公開發(fā)表文獻卻極少。文獻[9-10]分別推導了帶有攻擊時間約束、攻擊時間與攻擊角度約束的最優(yōu)導引律。文獻[11]采用數(shù)值優(yōu)化方法確定多導彈同時到達的指定時間,對攻擊時間控制的最優(yōu)導引律進行了一定程度的改進。趙世鈺等[12]將剩余時間作為協(xié)調(diào)變量并動態(tài)地進行估計,提出了基于協(xié)調(diào)變量的時間協(xié)同導引律。鄒麗等[13]將攻擊時間控制導引律與分散化協(xié)調(diào)算法相結(jié)合,提出了一種多導彈編隊齊射攻擊分散化時間協(xié)同導引律。黃漢橋等[14]以彈道偏角作為自變量對導彈非線性運動學方程進行了變換,利用極小值原理設(shè)計了具有攻擊時間和攻擊角度約束的導引律,但所得結(jié)果可能存在奇異問題。針對目標信息事先已知的情況,文獻[15]先離線解算出滿足攻擊時間及攻擊角度約束的視線角速率期望軌跡,然后應(yīng)用滑模變結(jié)構(gòu)控制方法使實際視線角速率跟蹤此期望軌跡,從而給出了一種滑模制導律。文獻[16]采用分階段控制方法設(shè)計了攻擊時間與攻擊角度控制的三維導引律。

以上有關(guān)攻擊時間控制的文獻均假定導彈速度定常,而考慮導彈速度非定常的帶有攻擊時間約束的閉環(huán)導引律研究未見相關(guān)報導。事實上,導彈在實際飛行中總是存在或大或小的速度變化,某些導彈甚至會跨聲速飛行。本文正是圍繞導彈速度時變情況下的攻擊時間及攻擊時間與攻擊角度控制問題展開研究。為實現(xiàn)帶有時間約束的精確制導,需要較為精確的飛行剩余時間信息以形成控制反饋,而導彈速度的不確定變化給剩余飛行時間的預測帶來了一定的困難。然而,結(jié)合具體的實測數(shù)據(jù)及實際應(yīng)用背景,導彈的速度信息可認為是部分先驗已知的,因此能夠有效預測導彈速度的變化規(guī)律,進而獲得剩余飛行時間信息。

1 問題描述

目標靜止,設(shè)指定的攻擊時間與攻擊角度分別為Td與θd。導引方程可描述為:

(1)

式中,R,q,θ與φ分別為彈目距離、目標視線角、導彈的飛行路徑角與前置角;V為當前時刻導彈的速度;an為導彈的法向加速度,即控制量。

用tf與θf分別表示導引的終端時刻及導引結(jié)束時的飛行路徑角(即攻擊角度),那么攻擊時間約束可以描述為通過控制作用使tf=Td,攻擊時間與攻擊角度約束可以描述為通過控制作用使tf=Td,θf=θd。

本文的導引律設(shè)計思路采用比例導引(PN)或偏置比例導引(BPNIAC)附加反饋項的方法,注意V不能當作常值處理。

2 攻擊時間控制的導引律設(shè)計

首先解算導彈在PN下的實際剩余航程,并根據(jù)指定的攻擊時間構(gòu)造標稱剩余航程,然后通過在PN基礎(chǔ)上附加反饋項使實際剩余航程收斂于標稱值,從而實現(xiàn)攻擊時間的控制。

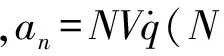
(2)

記r=R/R(0),由式(2)可得:

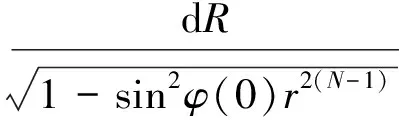
(3)

對式(3)在[0,tf]區(qū)間內(nèi)進行積分,得:

(4)

式中,左端的積分代表初始時刻導彈的剩余航程,記為L(0)。那么t時刻導彈的剩余航程為:

(5)

由泰勒公式處理式(5)右端的積分項,可得:

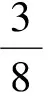
(6)

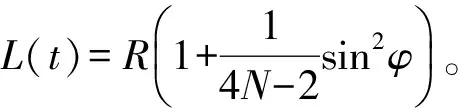
構(gòu)造標稱剩余航程為:

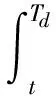
(7)

顯然有

(8)

注意到導彈以實際速度沿標稱剩余航程運動時,其到達目標點的時間為Td。因此,當L(t)=Ld(t)時,導彈采用PN即可實現(xiàn)攻擊時間控制;當L(t)≠Ld(t)時,在PN的基礎(chǔ)上附加一個控制項使L(t)→Ld(t),期望導彈經(jīng)歷Ld(t)這樣一段航程。因此,設(shè)

(9)

式中,aΔL為附加的反饋控制項,用于調(diào)整比例導引剩余航程與標稱剩余航程的差值。此差值用ΔL表示:

ΔL=Ld-L

(10)

對式(6)求導并將式(1)、式(9)代入,結(jié)合式(8)、式(10),整理可得:

(11)

為使ΔL→0,選取

aΔL=-k1sinφcosφΔL

(12)

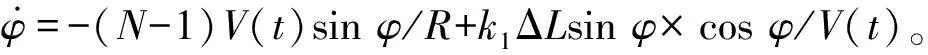
3 攻擊時間與攻擊角度控制的導引律設(shè)計

(13)

由式(13)中的第3式除以第二式并在[0,t]區(qū)間內(nèi)積分,可確定φ與α的函數(shù)關(guān)系。從而仿照第2節(jié)的公式推導,可得導彈在BPNIAC下的剩余航程為:

L(t)=ReC1φ2+C2(φ+α)2(1+C3φ2+C4φα+C5α2)

(14)

其中:

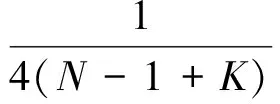
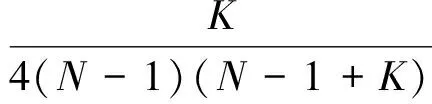
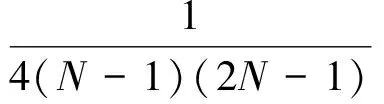
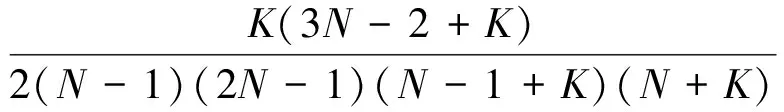
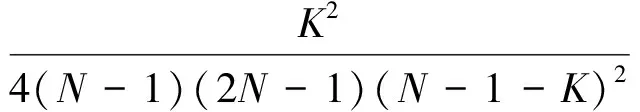
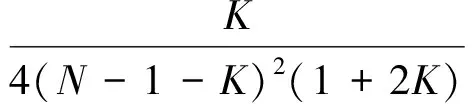
采用同第2節(jié)相類似的剩余航程反饋控制設(shè)計思路(推導過程不再贅述),可得:

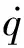
(15)

式中,f(φ,α)=2C1(1+C3φ2+C4φα+C5α2)φ+(2C3-C4)φ+(C4-2C5)α,系數(shù)k2取適當?shù)恼怠?/p>

4 仿真結(jié)果與分析

選擇目標位置為坐標原點(0,0),導彈初始位置為(-11,0.5)km,導彈速度的變化規(guī)律設(shè)定為V(t)=250+20t+2 sint-0.3t2,初始航向角為30°,過載限制為8,指定的攻擊時間為30 s,指定的攻擊角度為0°。采用本文的導引律,為闡述方便,將攻擊時間控制的導引律簡記為ITCG,將攻擊時間與攻擊角度控制的導引律簡記為ITIACG,導引律中的參數(shù)取N=3,K=1.5,k1=0.5,k2=2。應(yīng)用實際速度曲線的仿真結(jié)果如圖1所示。

仿真結(jié)果表明,應(yīng)用實際速度曲線時,也就是當預測的速度變化規(guī)律完全準確時,第2節(jié)給出的ITCG能夠保證攻擊時間控制的實現(xiàn),攻擊時間誤差為0.01 s;第3節(jié)給出的ITIACG能夠保證攻擊時間與攻擊角度控制的實現(xiàn),攻擊時間誤差為0.01 s,攻擊角度誤差為0.003°。應(yīng)用預測速度曲線時,ITCG的攻擊時間誤差為0.38 s,ITIACG的攻擊時間誤差為0.48 s,攻擊角度誤差為0.005°。由圖1(b)可知,為了調(diào)整剩余飛行航程誤差,控制指令在導引前期較大。而在飛行過程中ITIACG較ITCG需要更大的控制能量,這是因為ITIACG不僅需要調(diào)整剩余航程誤差,而且需要調(diào)整攻擊角度誤差。圖2(b)表明,ITCG與ITIACG能夠使導彈的實際剩余航程跟蹤由預測速度曲線構(gòu)造的不斷更新的標稱剩余航程。

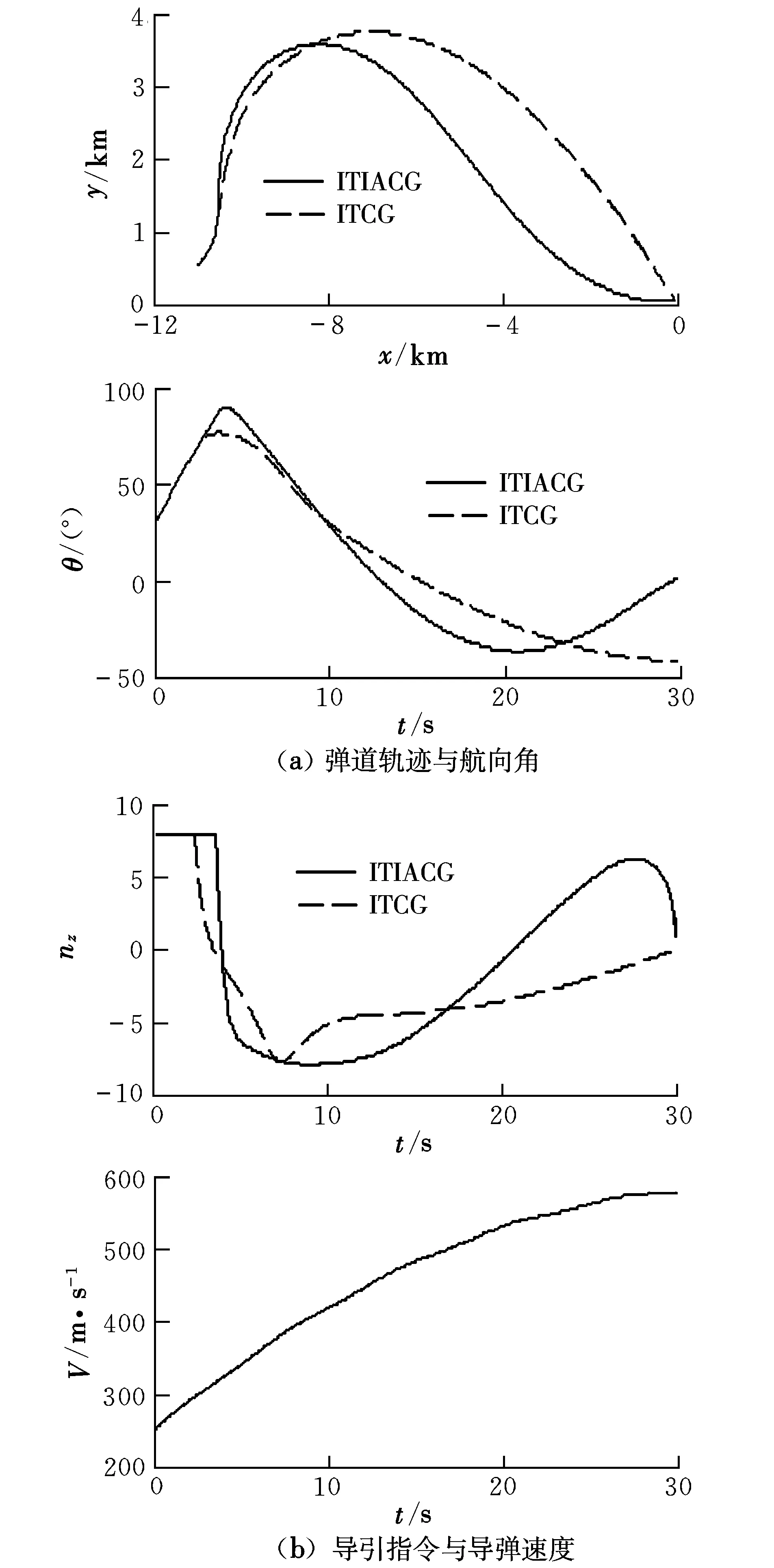
圖1 應(yīng)用實際速度曲線的仿真結(jié)果Fig.1 Simulation results using true velocity curves

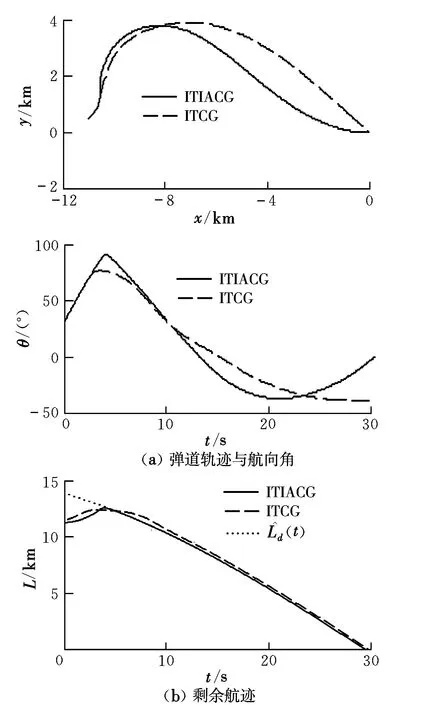
圖2 應(yīng)用預測速度曲線的仿真結(jié)果Fig.2 Simulation results using predicted velocity curves

5 結(jié)束語

為解決速度變化情況下的精確制導問題,本文推導了兩種帶有攻擊時間約束并考慮導彈速度變化的導引律,即速度隨時間變化時以PN為基礎(chǔ)的攻擊時間控制導引律和以BPNIAC為基礎(chǔ)的攻擊時間與攻擊角度控制導引律。通過設(shè)定攻擊時間與攻擊角度,可將所得導引律用于速度變化情況下的多導彈協(xié)同制導。

[1] Jeong S K,Cho S J,Kim E G.Angle constraint biased PNG[C]//Proceedings of the 5th Asian Control Conference.2004:1849-1854.

[2] Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constraint [J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.

[3] Ryoo C K,Cho H,Tahk M J.Optimal guidance laws with terminal impact angle constraint [J].Journal of Guidance,Control,and Dynamics,2005,28(4):724-732.

[4] Ryoo C K,Cho H,Tahk M J.Closed-form solutions of optimal guidance with terminal impact angle constraint[C]//Proceedings of the 2003 IEEE Conference on Control Applications.2003:504-509.

[5] Shin S J,Song T L.Time-optimal impact angle control for vertical plane engagements [J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(2):738-742.

[6] Ryoo C K,Cho H,Tahk M J.Time-to-go weighted optimal guidance with impact angle constraints [J].IEEE Transactions on Control Systems Technology,2006,14(3):483-492.

[7] Sang D,Min B M,Tahk M J.Impact angle control guidance law using Lyapunov function and PSO method[C]//Proceedings of the Annual SICE Conference.2007:2253-2257.

[8] Kim K S,Jung B,Kim Y.Practical guidance law controlling impact angle [J].Journal of Aerospace Engineering,2007,221(1):29-36.

[9] Jeon I S,Lee J I,Tahk M J.Impact-time-control guidance law for anti-ship missiles [J].IEEE Transactions on Control Systems Technology,2006,14(2):260-266.

[10] Lee J I,Jeon I S,Tahk M J.Guidance law to control impact time and angle [J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(1):301-310.

[11] Arita Shunsaku,Ueno Seiya.Improvement of guidance law for simultaneous attack[C]//SICE Annual Conference 2011.Waseda University,Tokyo,Japan,2011:1807-1812.

[12] 趙世鈺,周銳.基于協(xié)調(diào)變量的多導彈協(xié)同制導[J].航空學報,2008,29(6):1605-1611.

[13] 鄒麗,周銳,丁全心.多導彈編隊齊射攻擊分散化協(xié)同制導方法[J].航空學報,2011,32(2):281-290.

[14] 黃漢橋,周軍,郭建國.具有角度和時間約束的導彈最優(yōu)全彈道設(shè)計[J].西北工業(yè)大學學報,2010,28(2):165-170.

[15] Harl N,Balakrishnan S N.Impact time and angle guidance with sliding mode control [J].IEEE Transactions on Control Systems Technology,2012,20(6):1436-1449.

[16] 張友根,張友安.控制撞擊時間與角度的三維導引律:一種兩階段控制方法[J].控制理論與應(yīng)用,2010,27(10):1429-1434.

[17] Cho H,Ryoo C K,Tahk M J.Implementation of optimal guidance laws using predicted missile velocity profiles [J].Journal of Guidance,Control,and Dynamics,1999,22(4):579-588.

Impacttimeandimpactanglecontrolguidancelawformissileswithtime-varyingvelocity

MA Guo-xin, ZHANG You-an

(Department of Control Engineering, NAAU, Yantai 264001, China)

Two guidance laws which meet the requirements of impact time constraint, impact time and impact angle constraint respectively are proposed for the cooperative guidance for unsteady-velocity missiles. Firstly, by solving the system differential equations as missile was guided by the proportional navigation (PN) and the biased proportional navigation with impact angle constraint (BPNIAC), the actual lengths-to-go of the missile were derived, and the standard lengths-to-go were constructed from the designated impact time and the actual velocity profiles of the missile, then the impact time control problem was transformed into the problem of tracking the standard lengths-to-go for the actual lengths-to-go of the missile. Secondly, by adding a feedback control to PN and BPNIAC to drive the actual lengths-to-go of missile to track the standard one, the requirements for the impact time control of missile were achieved when the velocity of the missile was time-varying. Simulation results show the validity of the proposed approach. In the actual applications, the predicted velocity profiles and the on-line update strategy can be used to estimate the standard lengths-to-go.

proportional navigation; impact time; impact angle; time-varying velocity; cooperative guidance

TJ765.3

A

1002-0853(2013)03-0255-05

(編輯：崔立峰)