某高速公路瀝青路面維修處治方案有限元分析
王必賢 趙 婷
(1.長沙理工大學,湖南長沙 410076;2.中交第二公路勘察設計研究院有限公司,湖北武漢 430100)
1 概述
我國已經基本完成高速公路網的建設,瀝青路面以其行車舒適,維修方便和通車快等特點成了中后期高速公路的主要形式,由于我國超載超限問題十分嚴重且普遍,新建公路很快便產生了早期破壞,最具代表性的就是車轍,路面產生車轍后使得車輛行駛時難以操控,威脅行車安全,而且會導致路面積水,滲入基層造成路面結構破壞,縮短瀝青路面使用壽命。現在車轍已經成為路面養護工程中最重要環節之一。車轍深度達到一定程度時,就只能銑刨后重新罩面,但對罩面的日后的效果和維持時間沒有進行定量的分析與預測,因此采用有限元方法研究分析對瀝青路面車轍采取處治措施之后的效果,為日后的養護工作提供參考和借鑒,具有十分重要的意義。
2 加鋪層路面結構類型選擇
對高等級瀝青路面進行養護,一般常用的方法是以公路等級、交通量、公路技術狀況評定結果(路面破損PCI、路面平整度RQI、路面車轍RDI、抗滑性能SRI和結構強度PSSI)等為依據,同時以路面結構強度指數PSSI為控制指標,再結合具體情況(如抗滑性能,車轍深度等)制定養護維修方案。本文采用某高速公路的8種典型路面結構形式進行數值計算,其結構形式如表1所示。
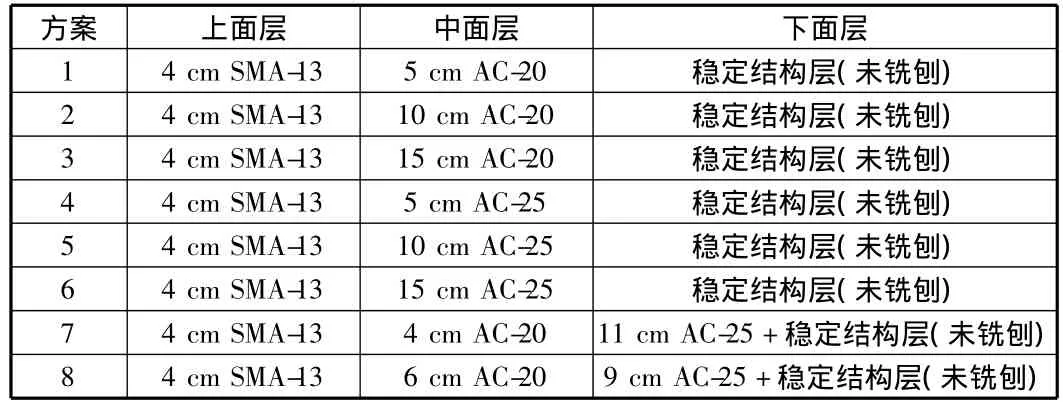
表1 8個路面車轍處治方案
3 路面材料參數選擇
本文采用ABAQUS有限元軟件的蠕變分析方法,對路面結構的車轍的產生過程進行模擬。加鋪瀝青混合料的蠕變參數和彈性模量均通過試驗得到,如表2所示,而對于不加鋪部分,則認為該層不參與路面結構的車轍變形,故只用彈性模量進行模擬。
4 荷載作用時間
建立有限元模型時,按照荷載應力等效原則,將雙圓均布荷載換算成矩形荷載:輪跡長×寬=19.2 cm×18.6 cm,間隙12.8 cm,荷載的累積作用時間按下式計算:

式中:t——荷載累積作用時間,s;
N——輪載作用次數,次;
P——車輛軸重,kN;
nw——軸的輪數,個;
p——輪胎接地壓力,MPa;
B——輪胎接地寬度,cm;
v——行車速度,km/h。
根據上述公式計算,可得一次軸載作用時間為0.008 64 s。

表2 瀝青混合料的蠕變參數和彈性參數
5 車轍深度數值模擬結果分析與比較
5.1 有限元分析結果
本文采用等參數四節點四邊形來構建二維路面結構模型,同時設置合理的邊界條件即左右無橫向位移,土基底面無豎向位移。同時采用楊氏彈性模量和蠕變特性來綜合模擬路面結構的車轍變形,計算車轍深度。
圖1~圖4給出了加鋪AC-20和AC-25不同厚度中面層經歷不同作用次數后的車轍深度,并建立關系式,如表3所示。

表3 瀝青重鋪厚度與車轍深度關系式
圖1,圖2關系曲線關于加鋪層厚度(cm)與車轍深度(mm)的關系曲線和相關系數如下。
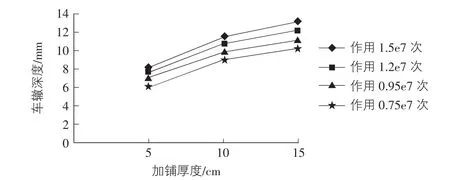
圖1 瀝青銑刨層加鋪厚度與車轍深度關系曲線圖(AC-20中面層)
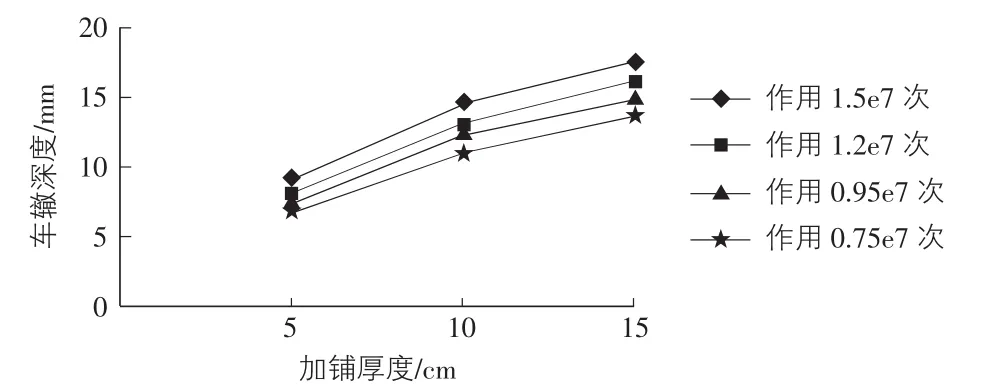
圖2 瀝青銑刨層加鋪厚度與車轍深度關系曲線圖(AC-25中面層)
同時比較不同工況下的曲線系數A和系數B如圖3,圖4所示。

圖3 系數和軸次關系曲線圖(AC-20)

圖4 系數和軸次關系曲線圖(AC-25)
由此可見,車轍深度為加鋪厚度、作用次數兩個參數共同作用的結果,對三者進行回歸分析,得到它們之間的數學模型為:

式中:H——車轍深度,mm;
h——加鋪中面層的厚度,cm;
N——標準軸載作用次數。
5.2 維修后車轍深度最小的最優方案
對于8個不同的方案,作用1 500萬次后,其對應的車轍深度如圖5所示。

圖5 1 500萬軸次作用于不同路面方案的車轍深度圖
可以看出,所加鋪瀝青層越薄,車轍深度越小,車轍深度隨著加鋪厚度的增加而增加。同時加鋪AC-20方案的效果優于AC-25方案和AC-20+AC-25的組合方案。
6 結語
1)本文通過有限元分析方法對8個不同加鋪方案的路面結構進行車轍模擬,分析車轍深度,作用次數和加鋪中面層厚度三者之間的關系,得到數學模型為:
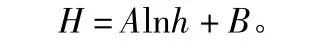
其中,H為車轍深度,mm;h為加鋪中面層厚度,cm;A=a ln N+b;B=c ln N+d,N為標準軸載作用次數。
2)對經歷過1 500萬次作用的8個加鋪方案進行計算,得到不同的車轍深度。結果表明,銑刨后加鋪瀝青層越薄,車轍病害越輕,隨著瀝青層厚度的增加,車轍反而越嚴重。而且加鋪AC-20中面層方案的抗車轍效果優于AC-25和AC-20+AC-25的組合。
[1]甄偉超.高速公路車轍的形成機理與處理措施[J].國防交通工程與技術,2004,2(2):27-29.
[2]王朝輝.瀝青路面加鋪技術研究[D].西安:長安大學,2008.
[3]安天崗.瀝青路面早期破壞現象與防護[J].山西建筑,2011,37(34):135-136.
[4]林繡賢.瀝青面層永久變形計算中有關參數的確定方法[J].中國公路學報,1989,2(2):8-17.
[5]閆翠香.濟青高速公路瀝青路面維修后車轍變化規律研究[D].濟南:山東大學,2010.

