云計算環境下的病毒傳播模型研究
陳秋霞, 陳宏偉
(湖北工業大學 計算機學院, 湖北 武漢 430068)
云計算是能夠提供動態資源池、虛擬化和高可用性的下一代計算平臺[1],然而云計算由于其用戶、信息資源高度集中,面臨的安全風險較傳統應用高出很多[2],一些學者提出了自己的安全防御模型[3].傳統的傳染病模型SIS、SIR、SEIR大量引入到病毒傳播模型的研究中,在傳統傳播模型的基礎上,許多學者從不同角度進行了相應的改進.文獻[4]提出了改進的SEIR模型,該模型結合病毒傳播SEIR模型和早期病毒爆發的數據來預測隨后的爆發和系統漏洞補丁對病毒的傳播的影響.病毒的狀態特性和網絡特性也影響著蠕蟲的傳播方式,文獻[5]建立了一個基于直接免疫條件下的SEIR病毒傳播動力學模型.
傳統的這類行為依賴于個體對病毒的檢測和補丁安裝,但是這種方式面臨著病毒特征庫不斷更新、規模過大而客戶端難以維系的問題,參加云計劃的客戶端收集可疑信息發送給數據處理中心,中心經過自動處理或人工分析識別出各類新威脅,并及時反饋到部署在網絡中的服務器群組成的云端,這樣不安全的鏈接或者惡意數據在云中直接被扼殺,從而阻止其進入用戶端,在網絡中而不是在客戶端進行病毒的查殺,云安全的病毒干預效果直接和參與可疑信息上報的用戶規模相關,同時也和病毒當時的規模相關,病毒感染的個體越多,參與云安全的個體越多,就有越多的可疑信息上報,導致對特定病毒識別的準確性更高,過濾效果更好.
本文組織如下:第1節給出了云安全網絡中的病毒傳播模型SEIR_C;第2節對SEIR_C模型進行了理論分析;第3節對全文進行總結.
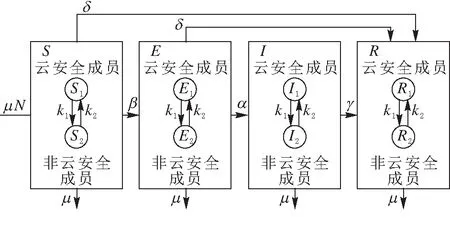
1 SEIR_C模型
云環境下的傳播模型應全力保護資源及行為不被危險破壞,為了保證云計算網絡在危險出現后提供正常服務,將感染個體進行隔離,使危險傳播控制在一定范圍內.相比于經典的SIR模型,傳統的SEIR模型采取了病毒隔離移除的措施,考慮了計算機病毒潛伏狀態,這樣就可以在病毒爆發前及早移除,結合云環境的特殊性,以此作為基本的模型更適合.本文研究的SEIR_C模型加入了云環境中安全成員的加入這一因素,在云環境中,SEIR_C 模型中具體的個體不論其處于4種狀態中的哪一種,S、E、I、R 這4個狀態之間的變遷是由于病毒感染導致的,并不會影響云安全成員狀態的改變,云安全成員越多,上報信息越豐富,使病毒信息更快的發現移除.由于基于大數量個體主機,可以使用平均場方法并用微分方程描述病毒傳播的平均趨勢,不需要考慮單個主機特殊事件的概率,假設新進入節點均為易感節點,總數N是不隨時間變化的常數,節點一旦進入R狀態,便不會再被傳染,模型不考慮病毒的感染時間,由上述假設,得到的SEIR_C模型見圖1,這里采用雙線性傳染率,則單位時間內新增的染毒節點(潛伏狀態)數為βSI,其中μ,α、δ、σ、β大于0小于1的數.由于云安全成員狀態的改變主要取決于初始狀態和用戶的動態修改,所以在一次的傳播過程中k1和k2初始值很小,可以認為SEIR_C模型的云安全成員比例是固定不變的k(0 表1 符號參數說明 圖 1 SEIR_C模型 從圖1可得到該傳播模型的微分方程表示形式如下: 病毒傳播實際是一個離散的事件,但是由于在云環境中存在海量的計算機個體數,這里可以作為連續的事件來處理,很多研究者提出這種處理方法,也得到了可行的驗證. 從公式(1)可以看到微分方程的復雜性,要求出它的解是很困難的,由于公式(1)前三個方程與R(t)無關,所以可以假設考慮公式(1)系統中的前三種狀態進行分析,即: 令γ+μ=a,δ+α+μ=b,δ+μ=c,則上述公式(2)方程組可以簡化為 如果要使得系統(3)是穩定的,則必須滿足以下微分方程組 (4) 當I=0時,系統(4)處于無病毒狀態,得到無病毒平衡點: 當I(t)> 0, 得到地方性病毒的平衡點 (5) 由公式(6)可以得到,λ1=-c<0,當R0≤1時,λ2<0,λ3<0; 無病毒平衡點是穩定的且是局部漸近穩定;當R0>1時,λ2>0,λ3<0,無病毒平衡點是不穩定的. 根據微分方程組(3)得到在局部病毒平衡點處有Jacobian 矩陣 J(Q1)= (9) 其所對應的特征方程為 (10) 在這里,d1=1 ,d2=a+b+c,d3=ac+bcR0,d0=abc(R0-1), , d1d2d3+d1-d1d3-d1d2>0 由Routh-Hurwitz判據,有Δ1=d1>0,特征值具有負實部,滿足Routh-Hurwitz 穩定性條件,所以局部病毒平衡點是穩定的. 本文從云安全的角度分析建立了一個基于主動免疫的SEIR_C模型,該病毒模型考慮了計算機病毒的潛伏性,同時考慮了現階段云在實際生活的逐步應用,越來越多的用戶使用也會對病毒的傳播造成影響.但是現階段云環境還存在著很多不確定的因素,這是今后進一步需要考慮和研究的內容. [參考文獻] [1] 陳 康,鄭緯民.云計算:系統實例與研究現狀[J]. 軟件學報,2009,20(05):1 337-1 348. [2] 馮登國,張 敏.云計算安全研究[J].軟件學報,2011,22(01):71-83. [3] 徐小龍,吳家興,楊庚. 一種基于Cloud-P2P計算模型的惡意代碼聯合防御網絡[J].計算機應用研究,2012,29(06):2 214-2 217. [4] Chuang M A, Yongjian YANG,Xiaoyu GUO.Improved SEIR viruses propagation model and the patch's impact on the propagation of the virus[J].Journal of Computational Information Systems,2013,9(08):3 243-3 251. [5] 趙君平.一類具有一般非線性隔離函數及潛伏年齡SEIRS傳染病模型穩定性分析[J].江西師范大學學報(自然科學版),2011,35(05):464-470.
2 穩定性分析
2.1 無病毒平衡點及穩定性分析

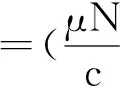
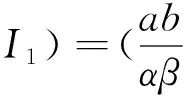
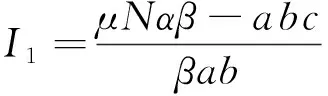
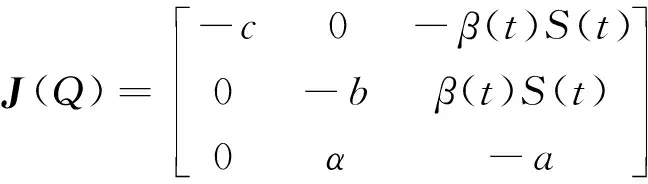
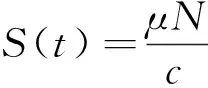
2.2 局部病毒平衡點及穩定性分析
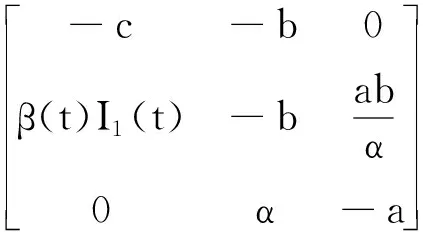
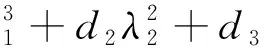
3 總結

