基于亮度不變特征的自適應雙邊濾波算法

康長青，徐格靜，項東升，趙永標

(湖北文理學院數學與計算機科學學院，湖北襄陽441053)

1 引言

圖像去噪是圖像處理和計算機視覺中的重要的基礎問題之一。如何在噪聲去除的同時最大程度保留邊緣細節是圖像去噪的一個難題。目前常見的邊緣保持濾波算法主要有各向異性擴散濾波［1－2］，非局部均值濾波［3－4］，過完備詞典學習［5－6］和雙邊濾波［7－12］等。

各向異性擴散濾波［1］主要采用梯度模值函數的局部擴散系數，使得圖像逐漸逼近，能在一定程度上保持圖像的邊緣，但是算法在理論上的不適定性，會造成處理過程的不穩定，使得算法處理的時間受噪聲方差影響嚴重;非局部均值濾波［3］主要利用圖像的自相似性冗余特征，通過對圖像的逐塊估計，相似度權重計算和加權平均來去噪，特別適用強紋理圖像處理，但是由于逐像素計算塊相似度，存在計算復雜度較高，不便于實時運用的缺點。過完備詞典學習算法［5］主要基于稀疏表示理論，通過設計適當的過完備字典，求解稀疏表示來進行濾波，但是該方法同樣存在計算量大、復雜度高的不足;相比以上算法，雙邊濾波算法［7］采用空間距離和亮度距離加權平均，計算簡單，實現容易，已經廣泛應用于彩色圖像處理領域和其他圖像處理與分析領域，主要缺點是難以確定合適的參數。

研究人員提出了各種雙邊濾波的改進算法。文獻［8］提出使用圖像的顯著度值來改進空間距離參數，缺點是忽略了亮度距離參數比空間距離參數受噪聲變化影響更明顯的特性。文獻［9］提出采用Stein的無偏風險估計的統計方法來確定最優參數，但是算法需要復雜的數值計算。文獻［10］提出使用平滑偏好函數來進行最優參數確定，存在依賴用戶偏好，自適應性缺乏的不足。文獻［11］提出在空間距離和亮度距離參數基礎上，增加一個局部特征濾波參數，增加了參數選擇的復雜性且不具有自適應性。由于上述算法采用的像素亮度差很容易受到噪聲的干擾，而相位一致性測度［13］是一個量綱一的量，具有不受圖像亮度或對比度變化的影響，符合人類視覺系統感知特性的優點，因此本文在雙邊濾波思想的框架下，集成相位一致性亮度不變特征，提出一種新的自適應的雙邊濾波算法。

2 雙邊濾波器的原理

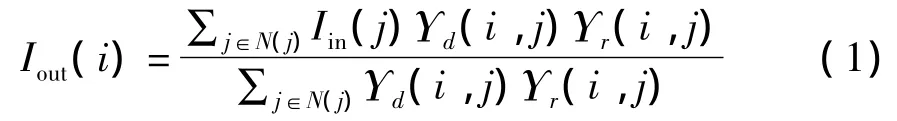
式中，Iin為原始圖像;Iout為濾波后的圖像;j為模板的中心像素點;N(j)是其鄰域;Υd(i，j)為空間距離函數;Υr(i，j)為亮度距離函數。這兩個距離函數的公式分別為:

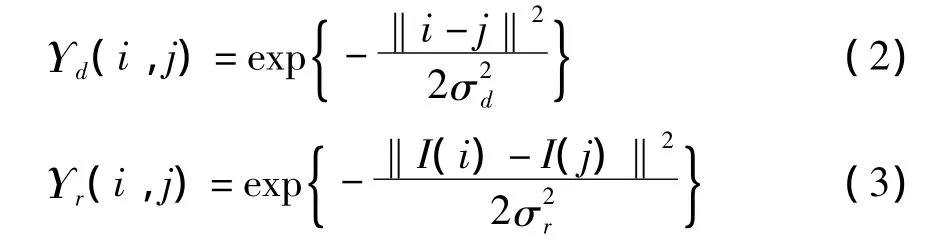
二維圖像的雙邊濾波器的濾波模型為:

式中，σd為空間距離標準差;σr為亮度距離標準差。

由以上公式可知，雙邊濾波器的權系數由鄰域間空間距離和亮度距離共同構成，也即取決于σd和σr的參數選擇。而參數的選擇主觀任意性較大，不具有對圖像亮度和噪聲方差的自適應性。當σd變大，參與濾波的像素個數增加，會造成圖像變得更模糊;如果σr對σd補償，隨著σr變大，像素亮度差的較大噪聲又會作為圖像邊緣被保留。參數的隨意選擇會造成圖像視覺質量的降低，如何進行參數的自適應設置變得非常有必要。

3 基于亮度不變特征的自適應雙邊濾波算法

3．1 空間距離參數σd的選擇

空間距離參數σd使用文獻［13］提出的相位一致性測度來確定。在位置為i、方位為θ的噪聲魯棒相位一致性特征函數表示為:

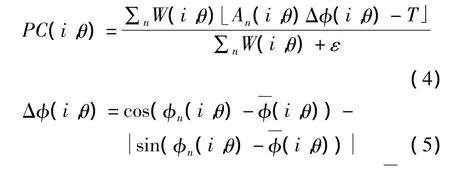
其中，An和Фn是在小波尺度n幅值和相位為加權平均相位;T是噪聲閾值;ε是為一個小的正數，是為了避免計算過程中上式出現除數為零的情況，符號?」表示表達式為正時取自身值，否則取0。

W(i，θ)是頻率傳播的權重因子，窄的頻率分布分配小的權值。W(i，θ)的值由頻率寬度決定，表示為:其中，c為加權函數的切斷值;g為增益因子，決定了切斷的鋒利程度;s(i，θ)為濾波器響應的頻譜寬度，表示為:

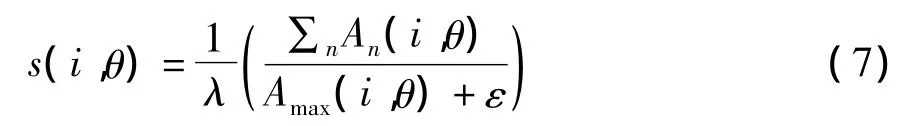
其中，Amax(i，θ)為在(i，θ)最大響應濾波器的相位;λ為小波尺度的總個數。

利用相位一致性特征函數，用公式(8)～(10)計算圖像中每一點的值:

求得圖像局部相位的最大矩M(i)和最小矩m(i)為:

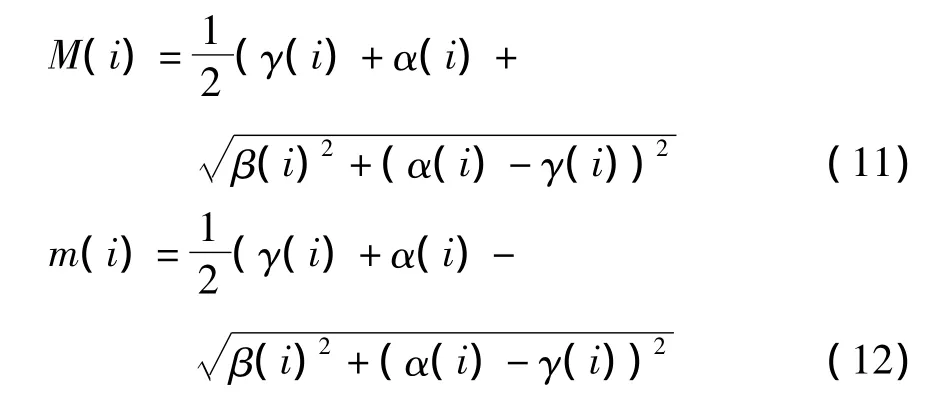
利用最大矩和最小矩，得到空間距離參數σd的表達式如下:

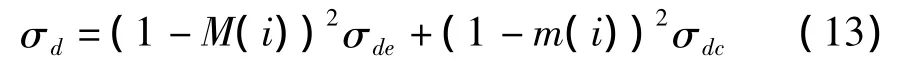
其中，σde為距離參數σd的邊緣信息約束;σdc為角點信息約束。這里 σde=1．45，σdc=0．55。

3．2 亮度距離參數σr的選擇

由于亮度距離σr和整幅圖像的噪聲方差直接相關。亮度參數應能夠隨著噪聲方差的變化自動調整，采用文獻［14］提出的灰度均一性測度方差估計算法，來建立亮度距離與噪聲方差的變化關系。

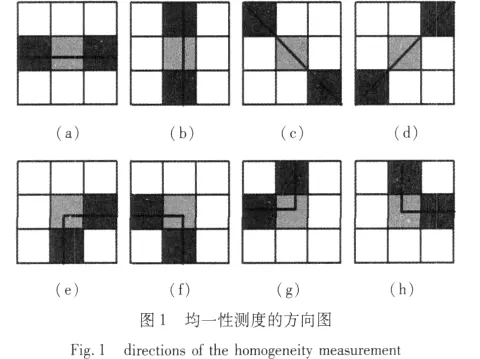
將含有噪聲的圖像I(i，j)分為大小相等圖像塊，設Bkl為以中心坐標(k，l)為中心，大小為W×W的圖像塊，塊的灰度均一性測度ξ可以用圖1中的八個方向進行測度。對于給定的任意方向，分配給塊的權重為{－1，－1，…，W－1，…，－1，－1}，相應像素的加權平均值表示這個方向的灰度均一度。當W=3時分配給的權重為{－1，2，－1}，圖中水平方向和垂直方向的灰度均勻度表示為:

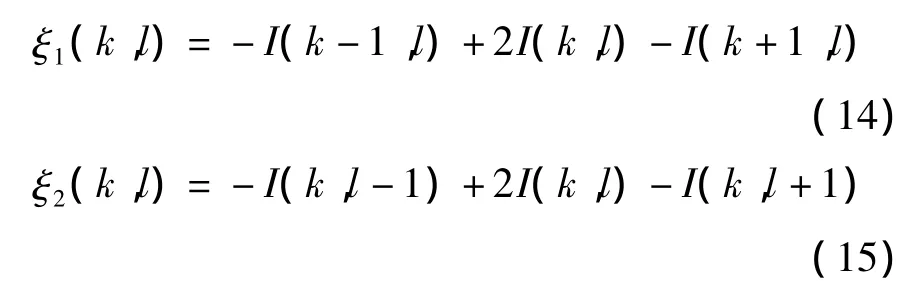
整個圖像塊的灰度均一性測度表示為:

當ξ≈0時，表示圖像塊均一性越好，選取這些均一性好的圖像塊來做為樣本方差塊，來估計圖像中的噪聲方差，可以表示為:

最終，建立亮度距離參數與噪聲方差的關系為:

其中，K為比例系數。

3．3 雙邊濾波的迭代計算

利用迭代算法，可以增強雙邊濾波器的去噪性能。為了防止多次濾波帶來的圖像結構性信息的丟失，確定迭代終止準則為:

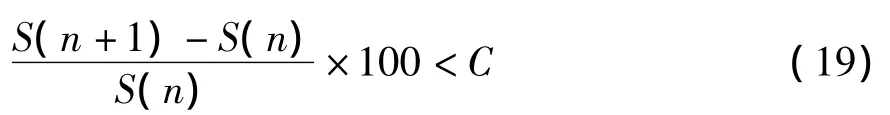
其中，S表示結構相似性指標［15］;C表示閾值;n表示迭代次數。

4 實驗結果與討論

為了驗證本文算法的去噪性能和邊緣保持特性，首先采用標準House和Monarch(512×512像素)作為測試圖像，分別應用文獻［7］、［8］、［11］的算法對不同高斯噪聲的圖像進行去噪實驗，并對比和分析相應的實驗結果。

圖2為在噪聲方差分別為20，30，40和100時，各種算法的峰值性噪比(PSNR)評價指標值。從圖中可以看出本文算法的去噪性能明顯高于文獻［7］和文獻［8］，略高于文獻［11］的算法。

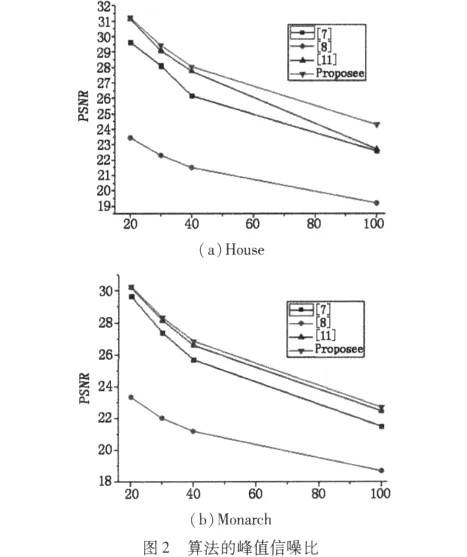
由于本文算法和文獻［11］的PSNR比較接近，圖3給出了House圖像在方差為30時的去噪效果圖，從圖3可以看出，本文算法得到了更加平滑的圖像區域和更明顯的邊沿特征，產生的紋理模糊小于文獻［11］，取得了更好的邊緣保持特性。

圖3 算法的效果圖

接著再對標準圖像庫邊緣特征明顯的Lena，Goldhill和Peppers圖像進行試驗，求出各種算法在上面定義方差下的PSNR，對所有五個圖像結果求平均值，得到算法的PSNR值如表1所示。從表中可以看出本文算法比原始雙邊濾波算法PSNR提高2．2 dB，比文獻［11］高出 0．49 dB。

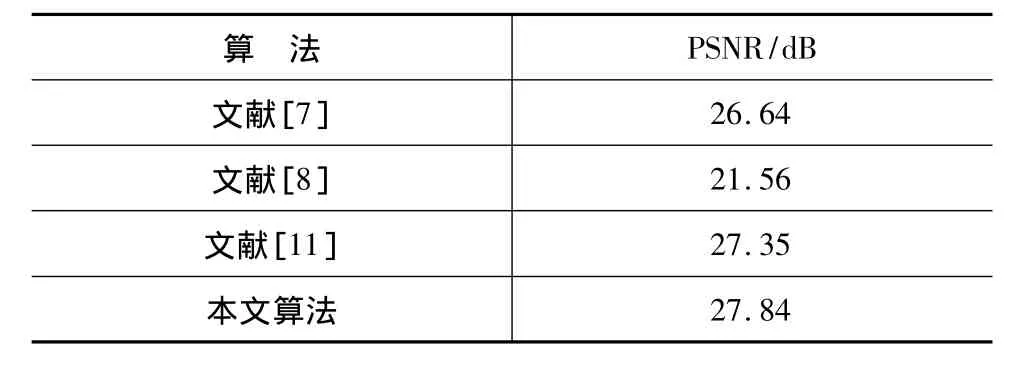
表1 算法的平均PSNR值

本文算法為迭代算法，在方差為40時大約需要5次迭代，迭代的次數會隨著方差的變大而增加，5次迭代所需處理時間為80 s左右。

5 結束語

本文提出了一種基于亮度不變特征的自適應雙邊濾波模型，分別采用相位一致性特征和灰度均一性測度來建立雙邊濾波器的空間距離參數和亮度距離參數的調整策略。實驗表明，算法具有計算簡單，魯棒性好，可以取得更好的圖像去噪性能和細節保持能力等優點。算法的不足之處在于處理時間略高，這將是作者下一步的努力方向。

［1］ PPerona，Jmalik．Scale-space and edge detection usinganisotropic diffusion ［J］．IEEE Transactions on Pattern A-nalysis and Machine Intelligence，1990，12:629 －639．

［2］ M Black，G Sapiro，D Marimont，et al．Robust anisotropic diffusion［J］．IEEE Transactions on Image Processing，1998，7(3):421 －432．

［3］ A Buades，B Coll，JMorel．A non local algorithm for image denoising ［C］//Proc．Int．Conf．Computer Vision and Pattern Recognition，2005，2:60 －65．

［4］ A Buades，B Coll，JMorel．Nonlocal image and movie denoising［J］．International Journal of Computer Vision，2008，76(2):123 －139．

［5］ M Elad，M Aharon．Image denoising via sparse and redundant representations over learned dictionaries［J］．IEEE Transactions on Image Process，2006，15(12):3736－3745．

［6］ JMairal，FBach，JPonce，etal．Online learning formatrix factorization and sparse coding［J］．Journal of Machine Learning Research，2010，11(1):19 －60．

［7］ Tomasi C，Manduchi R．Bilateral filtering for gray and color images［C］//Proc．Int．Conf．Computer Vision，1998:839－846．

［8］ Xie J，Heng P A，Shah M．Image diffusion using saliency bilateral filter［J］．IEEE Transactions on Information Technology in Biomedicine，2008，12(6):768 －771．

［9］ Peng H，Rao R．Bilateral kernel parameter optimization by risk minimization ［C］//Proc．Int．Conf．Image Processing，2010:3293 －3296．

［10］ Kisilev P，Freedman D．Parameter tuning by pairwise preferences［J］．IEEE Transactions on Information Technology in Biomedicine，2010，12(6):1 －11．

［11］ Butt I T，Rajpoot N M．Multilateral filtering:a novel framework for generic similarity-based image denoising［C］//Proc． Int． Conf． Image Processing，2009:2981－2984．

［12］ Lei Xiaojie，Gu Guohua，Sui Xiubao，et al．Improved temporal high－pass filter nonuniformity correction based on bilateral filter［J］．Laser ＆ Infrared，2012，42(7):831 －836．(in Chinese)

雷曉杰，顧國華，隋修寶，等．紅外雙邊濾波時域高通非均勻性校正［J］．激光與紅外，2012，42(7):831－836．

［13］ Kovesi P．Phase congruency:A low level image invariant［J］．Psychological Research，2000，64:136 － 148．

［14］ Amer A，Dubois E．Fast and reliable structure-oriented video noise estimation［J］．IEEE Transactions on Circuits and Systems for Video Technology，2005，15(1):113－118．

［15］ Wang Z，Bovik A C，Sheikh，et al．Image quality assessment:from error visibility to structural similarity［J］．IEEE Transactions on Image Processing，2004，13(4)，600－612．