改進滑模變結構永磁電機控制器研發

張自友，周大鵬

（樂山師范學院物理與電子工程學院，四川 樂山 614004）

0 引 言

永磁同步電機（permanent magnet synchronous motor，PMSM）是一個強耦合、非線性的系統，具有體積小、噪音小、轉動慣量小、功率密度高以及控制性能好等優點，目前已廣泛應用于數控機床、機器人航空等領域[1]。

為實現對PMSM的優良控制并保持穩定性，需要獲得轉子的準確位置信息，而傳統PMSM采用DTC直接轉矩控制系統，使用機械式位置傳感器既降低系統可靠性又增加了硬件成本[2]，因此，研究PMSM的無傳感器控制成為了PMSM的熱點問題[3]。

目前對PMSM進行無傳感器控制的主要工作有：采用空間凸級效應的PMSM控制方法能應用于各種速度和取得較好的估算效果，但具有高頻噪聲的缺陷[4]；采用狀態觀測器通過電機反電動勢提取位置信息的方法具有良好的動態特性，但不能對低速運轉時的轉子位置進行估計，因此，僅適用于中高速的轉子位置估計[5]。

滑模變結構控制器具有結構簡單和能適應各種速度寬度的優點，采用其設計的無傳感器PMSM控制器主要工作有：文獻[6]將徑向神經網絡RBF融入滑模控制器中，設計了以切換函數作為網絡輸入，以滑模控制器作為網絡輸出的神經滑模控制器。文獻[7]設計了一種基于T-S模型和滑模控制器的模糊滑模控制器，通過自適應技術對范數進行估計，通過T-S模糊局部補償器和滑模控制器構成全局控制器，使得全局閉環系統具有良好的跟蹤性能和魯棒性。文獻[8]設計了基于空間矢量脈沖調制技術的系統，采用PI控制器調節磁鏈，通過轉矩對電機空間矢量進行解耦，并通過轉子位置和定子電流對定子磁鏈進行估算。本文在上述工作的基礎上，提出了基于改進的滑模觀測器的PMSM控制器設計方法，并通過實驗證明方法的可行性。

1 PMSM數學模型

PMSM定子三相對稱繞組如圖1所示。

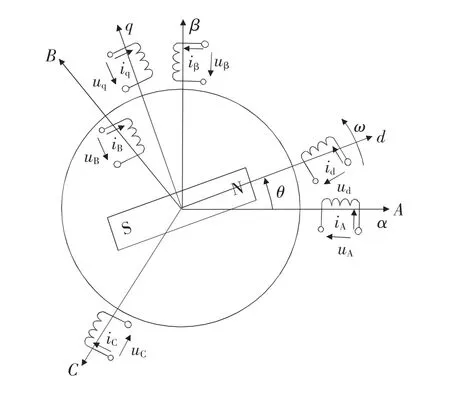
圖1 PMSM定子三相對稱繞組

根據基波合成磁動勢在坐標變換前后的等效原則，可以將PMSM在三相靜止坐標系A、B和C的數學模型變換到靜止的αβ坐標系下，對應的數學模型如式（1）所示：

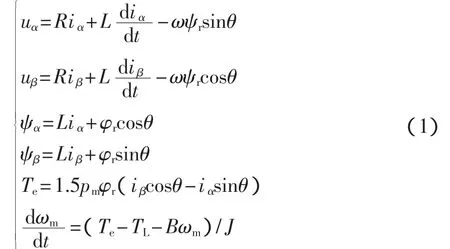
式中：L——α、β軸電壓電感；

uα，uβ——α、β 軸電壓；

iα，iβ——α、β 軸電流；

θ——轉子位置；

φr——轉子磁鏈；

ω，ωm——轉子電角速度和機械角速度；

pm——極對數；

Te，TL——電磁轉矩和負載轉矩；

R——定子繞組電阻；

B——摩擦系數；

J——轉動慣量。

2 傳統滑模變結構觀測器

滑模變結構控制器在運行過程中對開關函數sgn的符號進行判斷，不斷切換控制量來改變系統結構，并使得系統最終運動到切換面S=0上。

傳統的PMSM滑模變結構觀測器是通過對定子電流進行估計，然后與實際電流進行比較，最后通過兩者的誤差切換控制量實現控制，所以基于式（1），可以得到傳統的滑模變結構觀測器[3]：

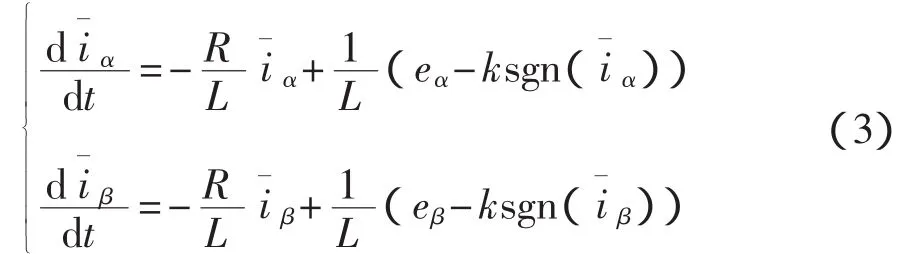
式中：k——滑模系數；

sgn（X）——開關函數，可以表示為

根據式（5）可以得到轉子角度估算值：

由于傳統滑模觀察器中采用sgn（X）為高頻開關信號，當在滑模面上進行滑模運動時，因開關空間和時間上的滯后，使得滑模觀測器出現了抖振現象，影響了轉子位置估算的準確性。

3 新型滑模變結構觀測器

3.1 低通濾波

傳統的滑模觀測器會出現抖振現象，因此，在傳統滑模觀測器的基礎上加入低通濾波器以消除抖振，如圖2所示。

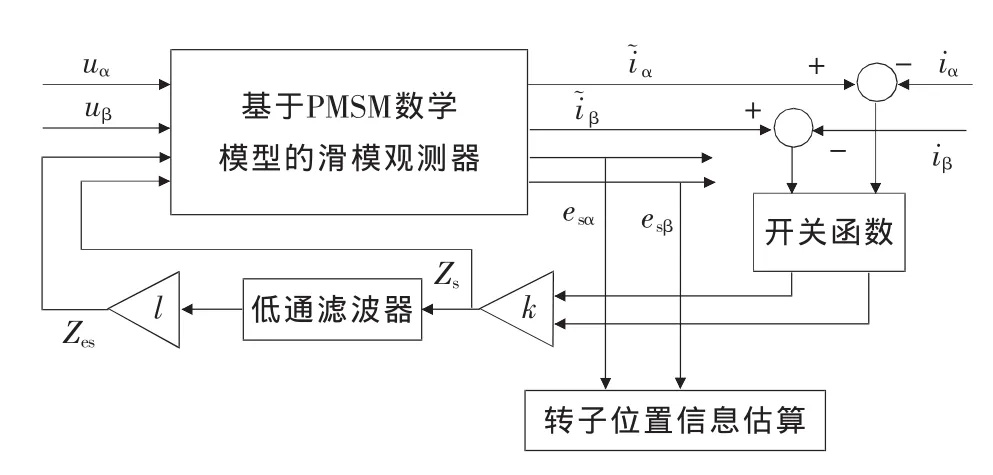
圖2 帶低通濾波器的滑模觀測器

ωth——低通濾波器的截止頻率。

將式（7）中的兩式相互除，可得PMSM的轉子轉角和轉速估計值：

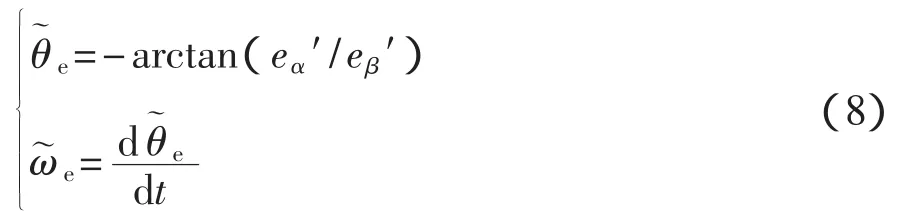
3.2 轉角相位補償

由于通過低通濾波得到的反電動勢估算轉子位置會出現偏差，使得相位滯后并隨轉子轉速的增加滯后程度加劇，所以，將滑模觀測器在圖2的基礎上進行改進，如圖3所示。增加了相位補償Δθ，加入相位補償后的滑模觀測器得到轉角估計值可以表示為

3.3 抖動消除

滑模運動時會產生高頻抖動，高頻抖動不僅會影響控制精度，甚至會使得系統振蕩失穩，因此，將準滑動模態控制思想加入到滑模觀測器中，即將系統運行軌跡限制在某一鄰域內，采用飽和函數取代開關函數，使得在邊界層內進行連續控制而在邊界層外切換控制以消除滑模抖振帶來的影響。

圖3 帶相位補償的滑模觀測器

飽和函數為

其中，θ為邊界層厚度，θ值的設置需要通過系統反復測試獲得，θ值過小會使得控制量過大，不能有效消除抖振；θ值過大，在消除抖動的同時卻使得系統穩定性和魯棒性降低。

采用飽和函數的滑模觀測器如圖4所示。

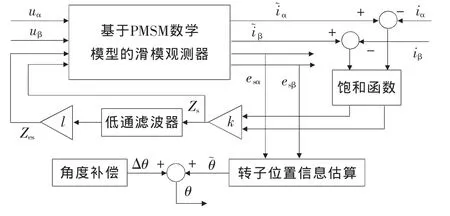
圖4 加入飽和函數的滑模觀測器

則改進的滑模觀測器可以表示為

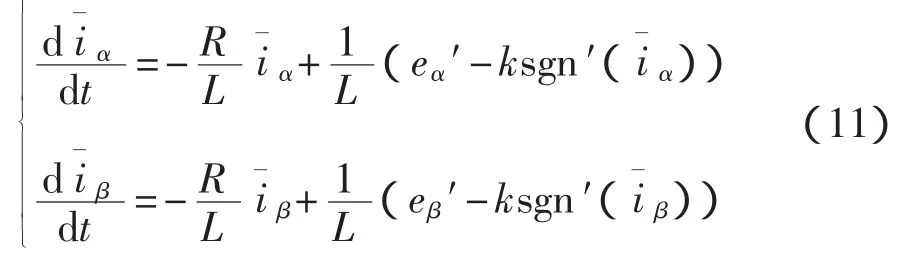
3.4 穩定性驗證

將其對時間進行微分，可以得到：

若式（13）小于 0，則式（11）所示的滑模觀測器是穩定的，此時有：

將式（11）代入式（14）可得：

4 系統測試

采用Simulink對其進行仿真與測試。初始化時實驗的具體參數：定子繞阻為0.5 Ω，定子相電感為9.5mH，定子相繞線自互感為4.5mH，轉動慣量為4.12 kg·m2，最大轉矩電流為10A，額定功率為0.8kW，額定轉速為2500r·min-1，低通濾波器的截止頻率為2MHz，參數k為1.25，邊界層厚度為20。

圖5和圖6展示了測量轉速與估算轉速、測量轉子位置和估計轉子位置隨時間變化的仿真曲線。可以看出本方法能較好地追蹤實際轉速和位置，具有較高的估算精度。在0.12s前，轉子的估算轉速有較小誤差，在0.12s后，估算轉速和實際轉速基本擬合，幾乎無誤差；同時可以看出轉子位置的估計值與測量值在仿真期間基本完全一致，具有較高的估算精度。

5 結束語

本文提出了一種基于改進滑模觀測器的永磁同步電機無傳感器控制方法，首先建立了永磁電機的數學模型，在此基礎上建立了以電流誤差為滑模面的滑模變結構觀測器，為了提高估算的精度和減少滑模運動中的高頻抖振，采用低通濾波對電流誤差開關信號進行濾波，并采用飽和函數取代開關函數，從而對切換函數進行了改進，通過李亞普若夫穩態判斷法驗證其穩定性。仿真實驗證明，本方法能較為準確地對轉速和轉子位置進行估算，是一種對PMSM進行無傳感器控制的有效方式。

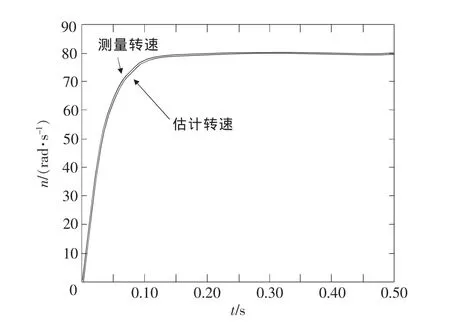
圖5 轉速仿真曲線

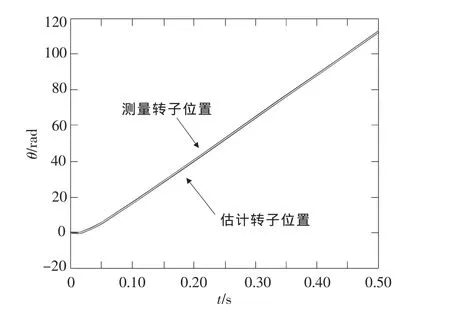
圖6 轉子位置仿真曲線

[1]王成元，夏加寬，楊俊友，等.電機現代控制技術[M].北京：機械工業出版社，2006.

[2]Sun D，Zhu J G，He Y K.A space vector modulation direct torque control for permanent magnet synchronous motor drive[J].IEEETransaction on Industry Applications，2003，39（6）：602－605.

[3]胡躍明.變結構控制理論與應用[M].北京：科學出版社，2003：74-84.

[4]趙德宗，張承進，郝蘭英.一種無速度傳感器感應電機魯棒滑模控制策略[J].中國電機工程學報，2006，26（22）：122-127.

[5]Lu W Q，Hu Y W，Huang W X.A hybrid approach of sensorless rotor position self-sensing for brushless DC motor[C]//InternationalConference on Electrical Machines and Systems.Wuhan：IEEE，2008：1334-1337.

[6]王武，白政民，姚寧.永磁直線同步電機神經滑模控制仿真[J].電機與控制應用，2011，38（2）：22-25.

[7]張細致，王耀南，袁小芳.永磁同步電機自適應模糊滑模變結構控制[J].中國機械工程，2010，21（2）：206-211.

[8]徐振宇，黃守道，黃科元，等.基于滑模變結構的PMSM直接轉矩控制[J].微特電機，2011，10（6）：44-47.