偽隨機信號（m序列）相關辨識的動態測試方法

何華鋒，李元凱，董海迪，楊學猛

（第二炮兵工程大學302室，陜西 西安 710025）

0 引 言

隨著測試技術的發展，人們對航空航天領域伺服系統動態測試的準確性與快速性提出了更高的要求。傳統動態測試采用相關函數法[1]，其測試過程如下：首先利用計算機控制交流D/A模件向被測系統加一定頻率的正弦信號，利用中速A/D采集響應輸出，由計算機進行相關函數運算，求出該頻率點的幅頻和相頻特性。測試中需要測量的頻率點有6個，而一個頻率點需要測量3個周期[2]，因此整個測試完成需要18個周期（約120s），不僅測試時間較長，而且僅得到6個頻率點的測量值。

本文針對航空航天領域伺服系統的動態性能測試要求，提出一種基于偽隨機信號相關辨識的動態測試新方法。

1 偽隨機信號相關辨識的動態測試方法

由于該測試方法是針對線性定常離散系統的，實際工程中可選用偽隨機二位式序列——m序列（周期信號）作為測試激勵信號[3]，整體結構如圖1所示。圖中 η（t）為輸入噪聲，ξ（t）為輸出觀測噪聲。假設整個系統中的采樣周期或步長與輸入m序列的步長Δ之比為1∶3，且假設輸入信號x（t）與噪聲η（t）、ξ（t）均為零均值的平穩隨機過程，彼此統計獨立。

首先利用數字計算機提供m序列m（k），經過數模轉換加到被測對象的輸入端；然后將輸出響應y（t）經模數轉換后得到y（k），送到計算機進行實時遞推計算，經若干周期后得到脈沖響應序列；最后利用Hankel矩陣法可以估算出被測系統的傳遞函數，從而得出被測對象的幅頻、相頻特性。

圖1 離散系統動態特性相關辨識法結構圖

2 m序列的自相關函數

在推導基于m序列離散形式相關辨識的計算公式之前，先說明一下m序列自相關函數的形式。可以證明，m序列自相關函數[4]為

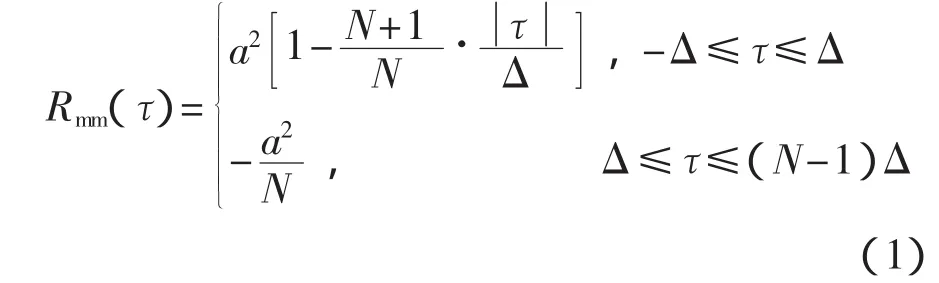
式中：a——m序列邏輯狀態“0”對應的輸出正電壓的幅值；

N——m序列一個周期的總拍數；

Δ——移位脈沖的周期。

由于離散化，可將式（1）簡化為[5]

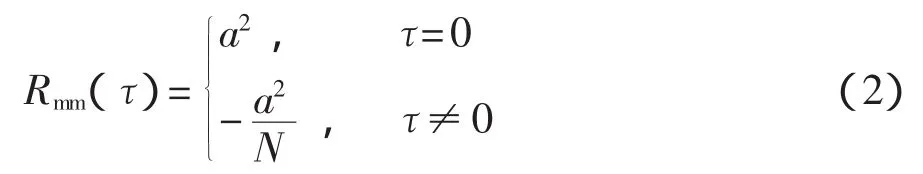
3 基于偽隨機信號相關辨識的動態測試原理

3.1 脈沖響應序列遞推公式

對于圖1所示的被測對象，根據卷積定理公式有

式中：g（σ）——被測對象的脈沖響應。

若將被測對象的動態方程寫成內部描述形式，有

當 x（0）=0 時，有

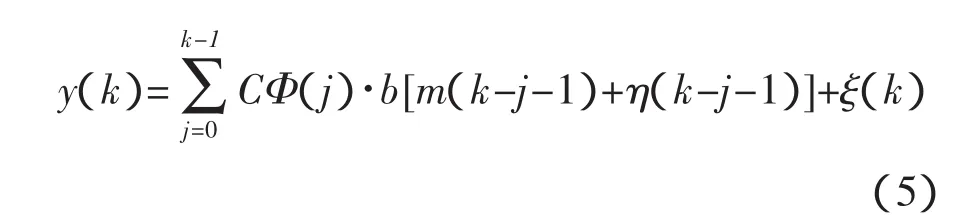
可知：Φ（j）b=g（j），將式（5）改寫為

設N為m序列一個周期的總拍數，且NΔ=T大于脈沖響應衰減到零的時間，將式（6）代入y（k）與m（k）的互相關函數，可得

式（7）中Rmm（σ）為m序列的自相關函數，這就是維納-霍普夫方程的離散形式。

取 σ=1，2，3，…，N，得

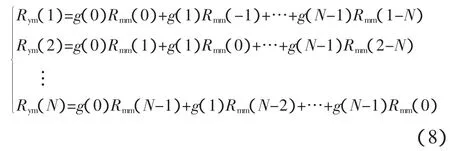
寫成矩陣形式，有

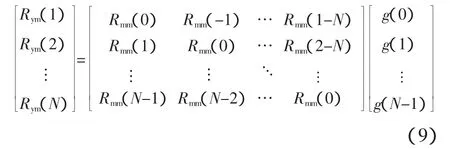
則有

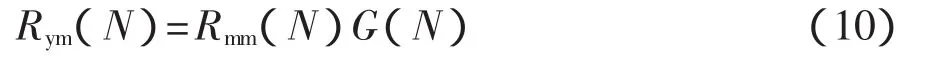
其中

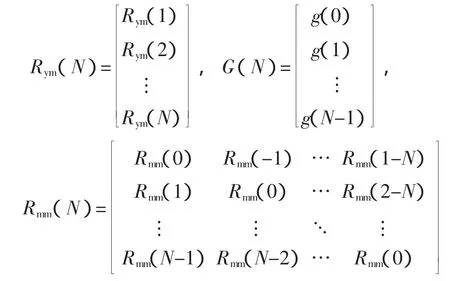
根據式（2）可得

因此

由式（12）可知，只要得到輸入輸出的互相關函數向量Rym（N），就可以利用其求出被測系統的脈沖響應G（N）。然而，Rym（1）、Rym（2）、…、Rym（N）不易直接精確求出，且為了能夠實現在線辨識，下面推導求脈沖響應G（N）的遞推公式。

根據第M次的測量，可按式（13）來估算輸入輸出的互相關函數

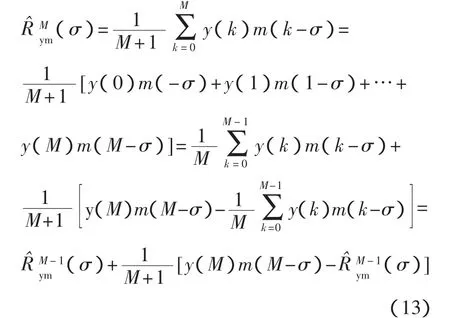
將式（13）代入式（12），可得第M次測量估算出的系統脈沖響應序列G^M（N）。

則有：

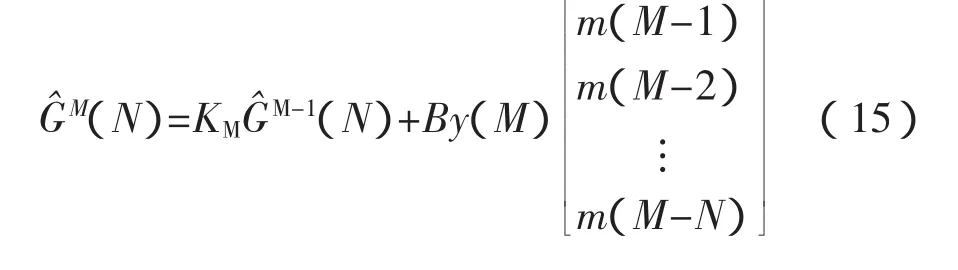
3.2 序列的參數選擇

以上討論了利用離散條件下偽隨機信號（m序列）相關辨識的方法對被辨識系統的脈沖響應序列進行估計的理論依據。在實際辨識中，需要根據被辨識系統動態性能的先驗知識，確定m序列的參數Δ、N和a[6]。通過分析m序列的自相關函數和功率譜密度可知：其自相關函數不是一個理想的周期脈沖，且功率譜密度也不是常值。但如果被辨識系統的工作頻帶處于（0~2π/3）Δ范圍之內，則可以將m序列近似看作理想的周期白噪聲。因此，設被辨識系統的最高工作頻率為ωmax，動態響應時間為ts，其參數應滿足ωmax<2π/（3Δ），且NΔ=（1.2~1.5）ts。

3.3 由脈沖響應確定傳遞函數的Hankel矩陣法

通過輸入偽隨機信號m序列，采樣輸出的響應信號進行實時的遞推計算，得到被測對象的脈沖響應序列的估計值。本節運用Hankel矩陣法[7]，利用脈沖響應的估計值來計算得出被測對象的脈沖傳遞函數系數的估計值。

設被辨識的離散系統模型是一個n階的脈沖傳遞函數

將式（16）化為相應的狀態轉移方程

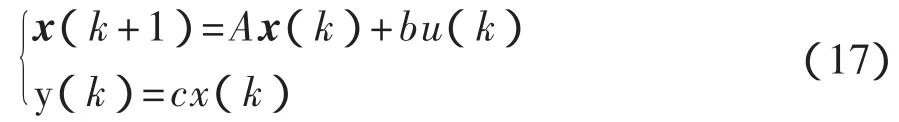
其脈沖傳遞函數又可以表示為

又因為

為互逆關系，則

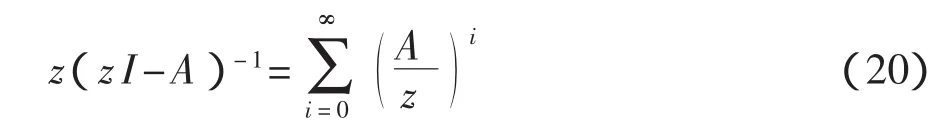
將式（20）兩邊同時除以z，可得

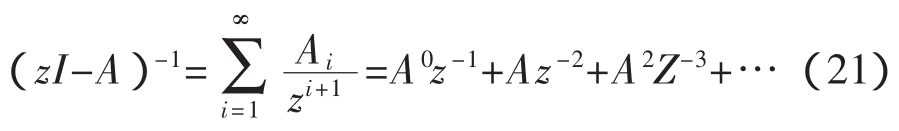
等式右邊取前n項代入式（18），可得脈沖傳遞函數與脈沖響應的關系式

將式（20）代入式（16）中，可得

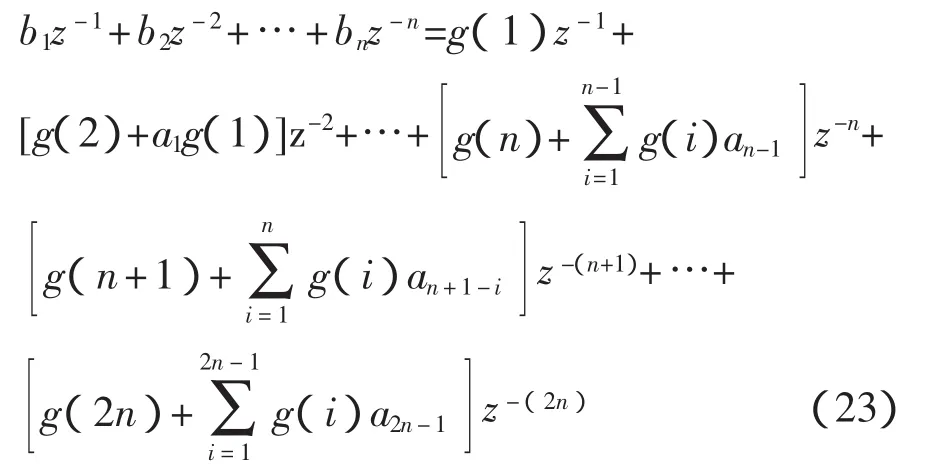
比較式（23）等號兩邊z的同冪次項系數可得

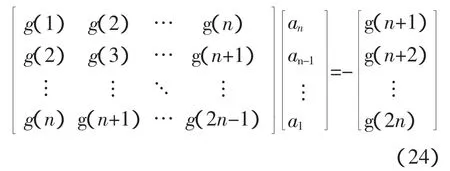
以及

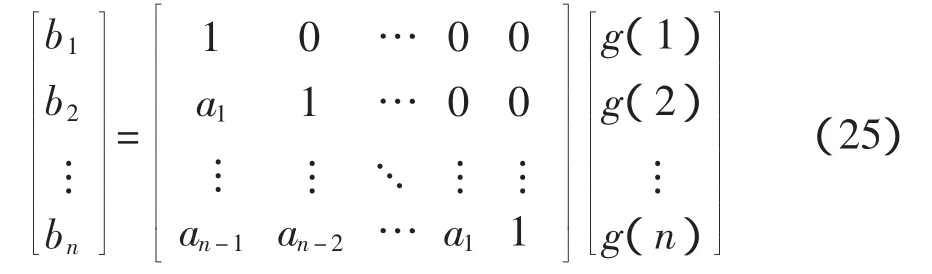
根據Hankel矩陣的定義可知，式（24）左邊的矩陣是一種待定的 Hankel矩陣，記作 H（n，l）。因此，將基于m序列相關辨識得到的被測對象的脈沖序列響應估計值代入式（24）和式（25）中，便可求得脈沖傳遞函數的估計值；經雙線性變換，可以得到連續傳遞函數的估計值；由估計的傳遞函數可求得幅頻和相頻特性[8]，完成動態測試。

4 驗證實驗

本節將利用基于偽隨機相關辨識的動態測試方法對傳遞函數標準化（即傳遞函數已知且固定）儀器設備的動態性能進行測試。實驗結果給出了被測對象的幅頻與相頻特性。

4.1 實驗模型

實驗模型結構如圖1所示，設整個系統中的采樣周期或步長與輸入m序列的步長Δ之比為1/3。已知被測系統的傳遞函數模型為

4.2 實驗參數

設被測系統最高工作頻率為1/5，動態響應時間為10s，則Δ的選擇范圍小于10.472s，若選Δ=1.5s，則可得N>10，選N=15。因此，輸入的m序列的周期T為22.5s，a值取0.5mA，系統采樣時間T0為0.5s，試驗進行3個m序列的周期（68s）。

4.3 實驗結果

運用該新方法經過3個m序列周期的測試后，遞推得到的被測系統脈沖響應序列數據如表1所示。

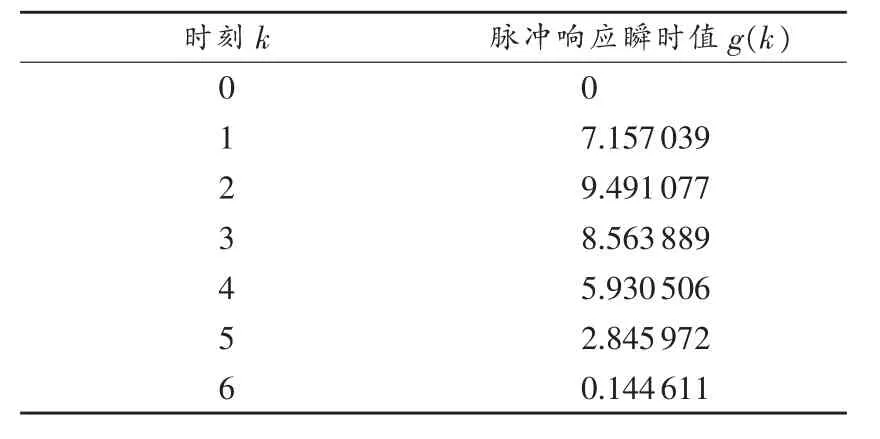
表1 脈沖響應序列數據（T0=0.5s）

由于被測系統的階數是3，構造的Hankel矩陣如下：

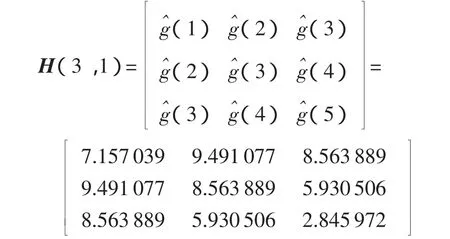
分別求得：

可得被測系統的脈沖傳遞函數的估計值為

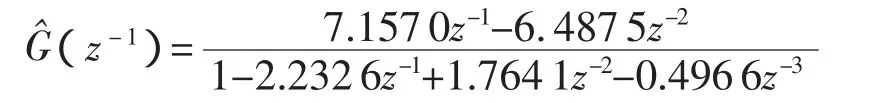
經雙線性變換后，連續傳遞函數的估計值為

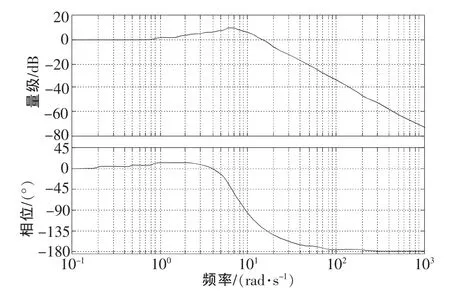
圖2 被測對象的對數頻率特性(Bode圖)

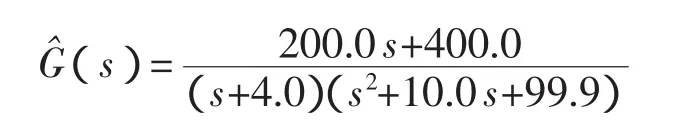
可見，估計的傳遞函數與標準化儀器的實際傳遞函數非常接近。根據估計傳遞函數可進一步求得被測對象的幅頻與相頻特性，如圖2所示。

5 結束語

由上述實驗結果可知，該方法在已知被測系統階數的情況下，可以獲得較好的近似傳遞函數；該方法運用于儀器設備的動態測試，可以準確地得到其幅頻與相頻響應；另外，傳統的動態測試方法需用時大約120s，使用該新方法可以節約用時約52s。

[1]崔吉俊.火箭導彈測試技術[M].北京：國防工業出版社，1999.

[2]胡昌華，馬清亮，鄭建飛.導彈測試與發射控制技術[M].北京：國防工業出版社，2010.

[3]王然冉，趙德平.用偽隨機信號相關辨識檢測線路的頻率參數[J].沈陽工業大學學報，1998（20）：46-49.

[4]李白男.偽隨機信號在工業系統辨識中的應用[M].北京：科學出版社，1987.

[5]趙淑清，鄭薇.隨機信號分析[M].哈爾濱：哈爾濱工業大學出版社，1999.

[6]王志賢.最優狀態估計與系統辨識[M].西安：西北工業大學出版社，2004.

[7]方崇智，蕭德云.過程辨識[M].北京：清華大學出版社，1988.

[8]盧京潮.自動控制原理[M].西安：西北工業大學出版社，2009.